08. 晶体管的交流工作分析
本文最后更新于 2025年6月4日 晚上
晶体管的交流工作分析
交流工作下的基极偏置
耦合电容
在交流状态下工作的电容器称为耦合电容,耦合电容的特性可以用一句话总结:耦合电容会阻碍直流分量并允许交流分量通过,即“隔直流,通交流”。
根据电容的容抗计算公式:\(X_c=\frac{1}{2πfc}\)
当直流分量通过电容时,电容的容抗会非常的大,电容视为断路。
当交流分量通过电容时,如果频率非常的高,则电容视为短路。一般认为\(X_c<0.1R\)(\(R\)为电路中的总电阻值)时,电容就视为短路。
在晶体管电路中,耦合电容的作用是阻止交流源电压源和输出电阻改变晶体管的静态工作点。
基极偏置电路分析
交流下的基极偏置电路如下图所示:
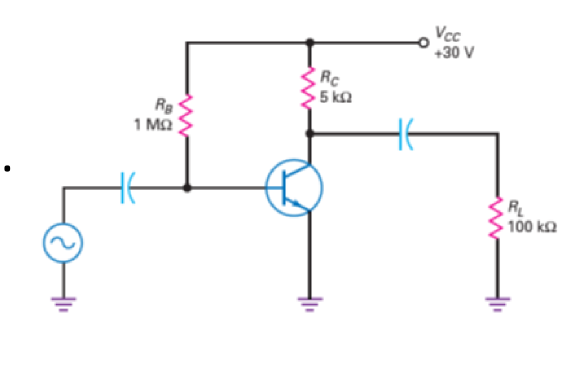
电路特点:
- 在输入端(基极)和输出端(集电极)各有一个耦合电容。
- 输入电压(即基极处的电源)\(v_{bb}\)是一个交流信号,不含有直流分量。
- 供电电压\(V_{CC}\)是一个直流信号,不含有交流分量。
当晶体管的基极和集电极存在耦合电容时,基极端的交流电源和输出端的输出电阻对晶体管的工作状态不会有任何的影响。
电路中所有的电流都可以分解为直流分量和交流分量两部分:
\[i_B=I_B+i_b\] 晶体管只会改变电路中电流的直流分量,交流分量保持不变。
因此,交流状态下的基极偏置只需要按照对应静态工作点计算出直流分量的值,在加上或减去交流分量即可。
需要注意的是由于\(v_C=V_{CC}-i_CR_c\),因此\(v_C\)的波形与\(i_C\)应当是反相的。由于\(i_C=βi_B\),因此\(i_B\)的波形与\(i_C\)同相。
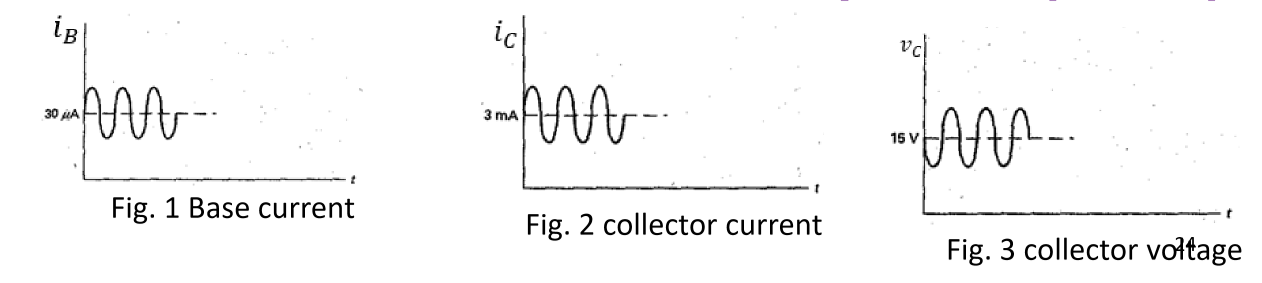
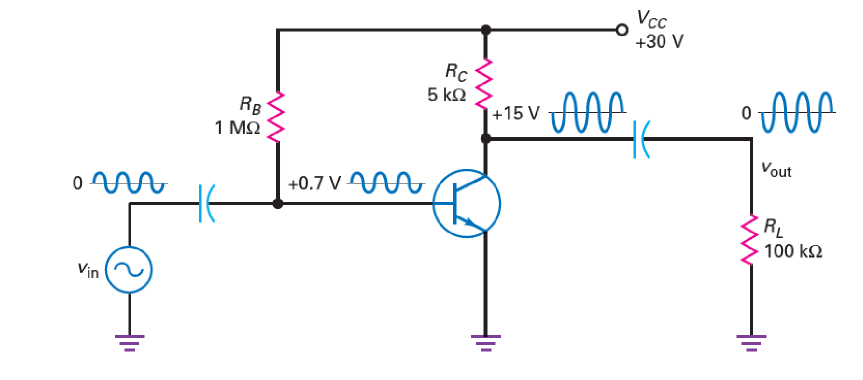
同时,由于耦合电容的特性,输出端的耦合电容会将直流分量完全去除,最终在输出电阻\(R_L\)上的电压/电流没有直流分量。
大信号模型
晶体管的大小信号模型针对基极的输入电压含有直流分量和交流分量时的电路进行分析。基极输入电压信号幅值较大时的电路分析模型称为大信号模型。
在大信号模型下,\(v_{BE}\)与\(i_C\)是非线性关系,两者之间满足:
\[i_C=I_Se^{\frac{v_{BE}}{V_T}}\] 其中\(I_S\)是\(I_C\)的饱和电流,\(V_T\)是晶体管在CB两点间存在温差而出现的电位差(热电压),在室温下约为25.9mV。
根据上述关系,可以将集电极的等效二极管近似看做是一个电压控制电流源,发射极的等效二极管保持不变:
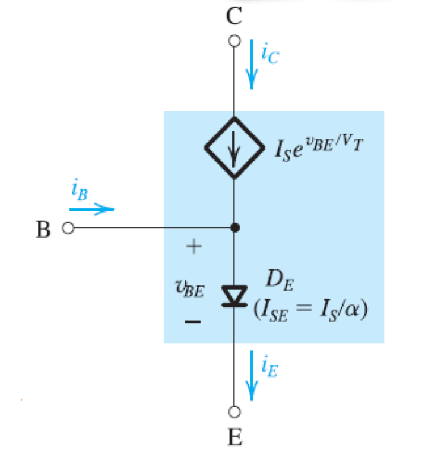
同时,希望在CE出导出输出电压,得到一个电压放大器(小的输出电压\(v_{BE}\)放大为\(v_{CE}\)),因此在集电极处加入一个电阻\(R_C\)。
那么,在大信号模型电路中输出电压\(v_{CE}\)与输入电压\(v_{BE}\)的关系如下图所示:
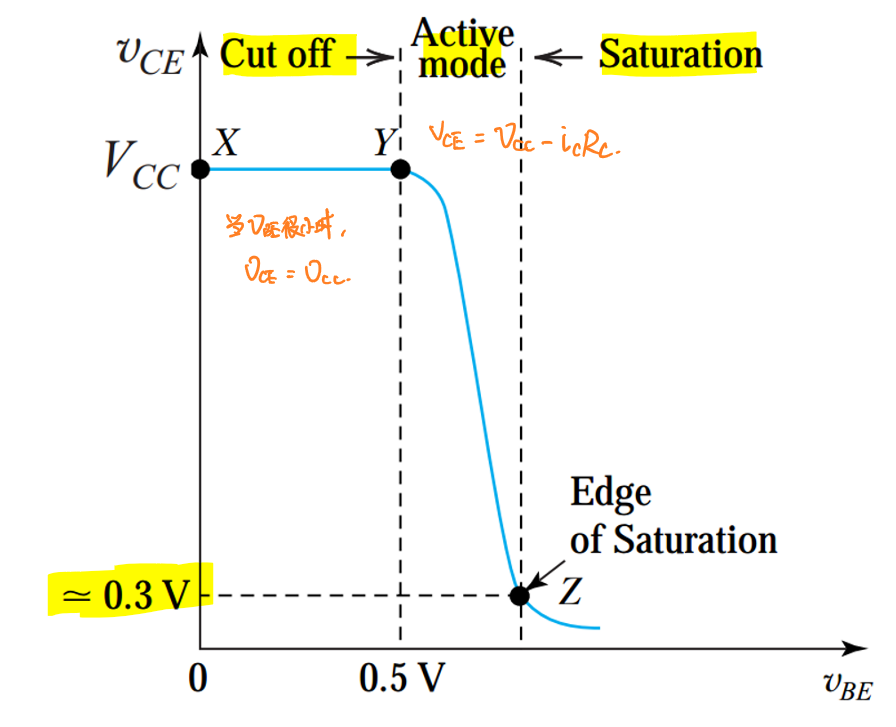
在大信号模型下,\(v_{BE}\)很容易超出放大模式区域,进入饱和工作状态,导致电路出现非线性失真。
小信号模型
基极输入电压的\(v_{BE}\)比较小,正好处于放大模式下时电路分析模型称为小信号模型。在小信号模型中,可以近似将\(v_{BE}\)与\(v_{CE}\)的关系视为线性,即将整个晶体管的工作状态视作直流工作状态。
小信号模型可以看做是大信号模型在放大模式下的表现。
电压变换特性
输入电压\(v_{BE}\)必须控制在一个小电压范围内,才能使晶体管的工作状态处于放大模式。在放大模式下: \[\begin{aligned}v_{CE}=&V_{CC}-R_Ci_C\\
=&V_{CC}-R_CI_Se^{\frac{v_{BE}}{V_T}}
\end{aligned}\] 通过上述公式可知,\(v_{CE}\)的波形与\(v_{BE}\)反相。
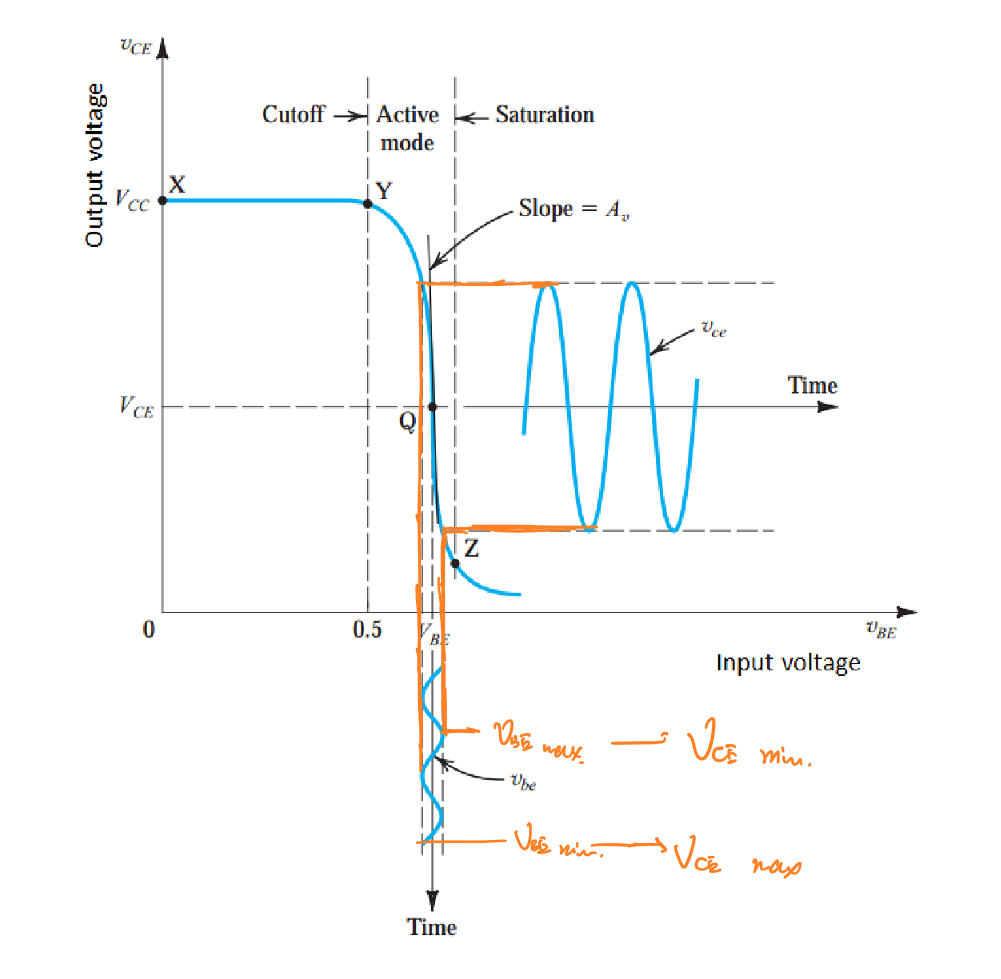
当\(v_{BE}=V_{BE}\)时,说明输入电压仅含直流分量,此时晶体管处于静态工作点。在该点对其求斜率得到(等效电压放大器的)直流电压增益:
\[A_v=\frac{dv_{CE}}{dv_{BE}}|_{v_{BE}=V_{BE}}\] 带入\(i_C\)的表达式,有:
\[A_v=-\frac{I_C}{V_T}R_C=-\frac{V_{CC}-V_{CE}}{V_T}\] 可以发现,在放大模式下,\(V_{CE}\)越低,直流电压增益越大。
小信号模型的电流分析
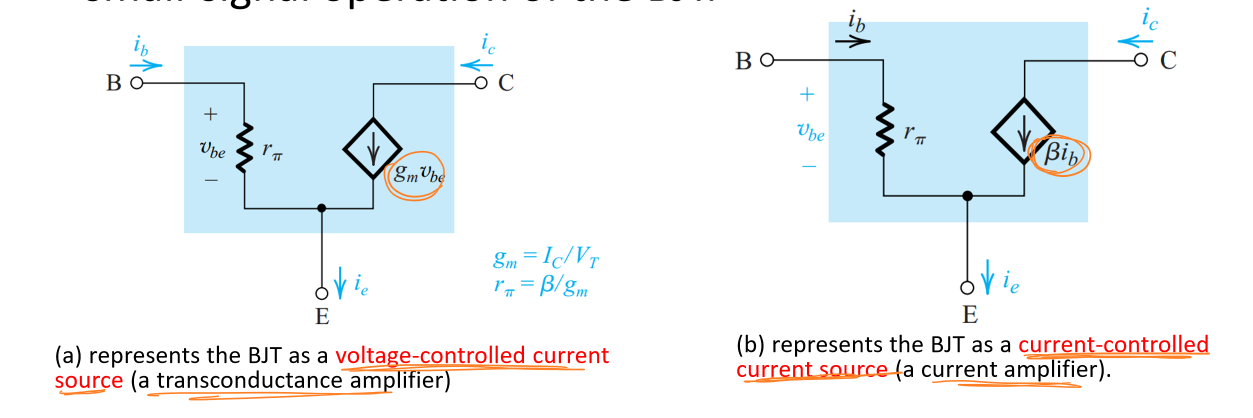
在小信号模型下,如果将\(v_{BE}\)视为输入信号、\(i_C\)视为输出信号,那么放大的结果是将小电压放大为大电流,这样的放大器称为跨导放大器。
那么对输出\(i_C\)引入输入\(v_{BE}\)进行分析:
由于小信号模型是大信号模型的一部分,因此\(i_C\)的导出式不变:
\[i_c=I_Se^{\frac{v_{BE}}{V_T}}\] 带入\(v_{BE}=V_{BE}+v_{be}\) \[\begin{aligned}
i_c&=I_Se^{\frac{V_{BE}+v_{be}}{V_T}}\\
&=I_Se^{\frac{V_{BE}}{V_T}}e^{\frac{v_{be}}{V_T}}
\end{aligned}\] 根据\(I_C=I_Se^{\frac{V_{BE}}{V_T}}\),有:
\[i_c=I_Ce^{\frac{v_{be}}{V_T}}\] 根据泰勒展开式,有:
\[i_c=I_C(1+∑_k(\frac{v_{be}}{V_T})^k\frac{1}{k!})\] 根据小信号模型的条件,\(v_{be}\)应当很小,\(b_{be}<<V_T\),此时泰勒展开式的高阶项可以全部被忽略,有:
\[i_C≈I_C(1+\frac{v_{be}}{V_T})\] 带入\(i_C=I_C+i_c\):
\[i_C=\frac{I_C}{V_T}v_{be}\]
跨导
定义\(g_m\)为跨导(Transconductance):
\[g_m=\frac{I_C}{V_T}\]
\(g_m\)是电流和电压之比,本质上是电导。
有:
\[i_C=g_mv_{be}\] 跨导也是\(i_C-v_{BE}\)图中当\(i_C=I_C\)时的斜率:
\[g_m=\frac{di_C}{dv_{BE}}|_{i_C=I_C}\] 带回\(A_v\),可以得到 \[A_V=\frac{v_{CE}}{v_{BE}}=-g_mR_e\]
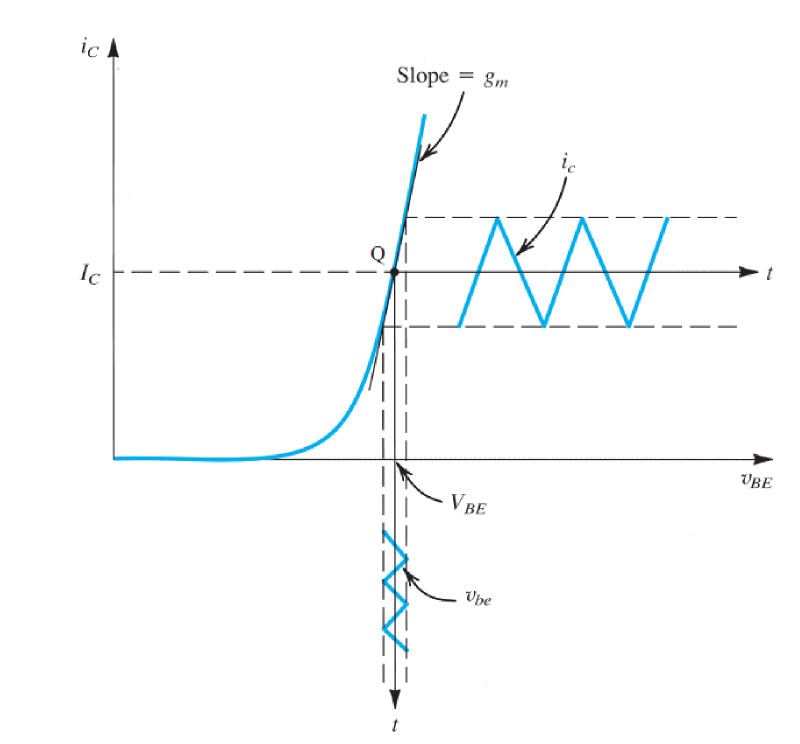
小信号模型中的直流分量和交流分量
由于小信号模型满足线性条件,因此电路中的直流分量和交流分量可以完全独立分别计算,然后将计算直流分量的结果与计算交流分量的结果相加。
小信号模型中,直流分量的作用是确定晶体管所处的静态工作点。
交流分量的作用是携带信息,因此在小信号模型中更关注交流分量的变化。
小信号模型的交流参数
小信号模型中直流分量的来源为集电极供电\(V_{CC}\)和基极供电\(V_{BE}\),令它们为0(接地)后进行交流分量的等效模型分析。
基极电流
由\(i_B=\frac{1}{β}i_C,i_C=g_mv_{be}\):
\[i_B=\frac{I_C}{β}+\frac{g_m}{β}v_{be}\] \[i_b=\frac{g_m}{β}v_{be}\]
输入阻抗
定义输入阻抗为输入端电压与电流之比。
当发射极接地,信号从基极输入时: \[r_π=\frac{v_{be}}{i_b}\] 带入\(v_{be}\)和\(i_b\),得到:
\[r_π=\frac{V_T}{I_B}=\frac{β}{g_m}\] 当基极接地,信号从发射极输入时:
\[r_e=\frac{v_{be}}{i_e}\] 带入\(v_{be}\)和\(αi_e=i_c\),得到:
\[r_e=\frac{V_T}{I_E}=\frac{α}{g_m}\] 可以发现输入阻抗\(r_π\)或\(r_e\)都不含有交流分量,是一个等效电阻。
厄利效应
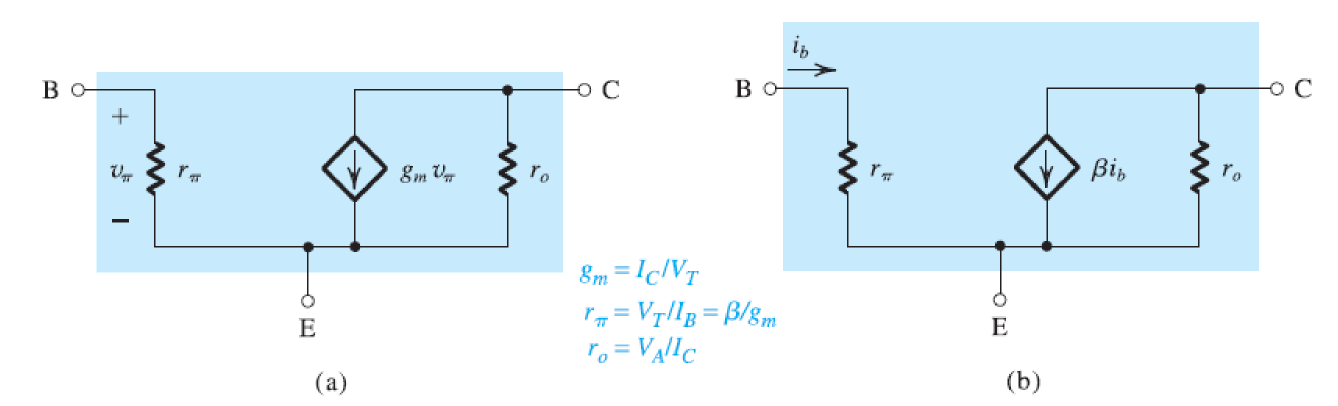
厄利效应/基区宽度调制效应(Early Effect),是指晶体管的\(V_{CE}\)改变,基极-集电极耗尽层宽度也会跟着改变。集电极电压升高,会使基极层变窄,使集电区或晶体管的输出电流增大。特性曲线中电压较大时的切线进行反向外推,其延长线与电压轴相交,在电压轴上截得的负截距称为厄利电压。
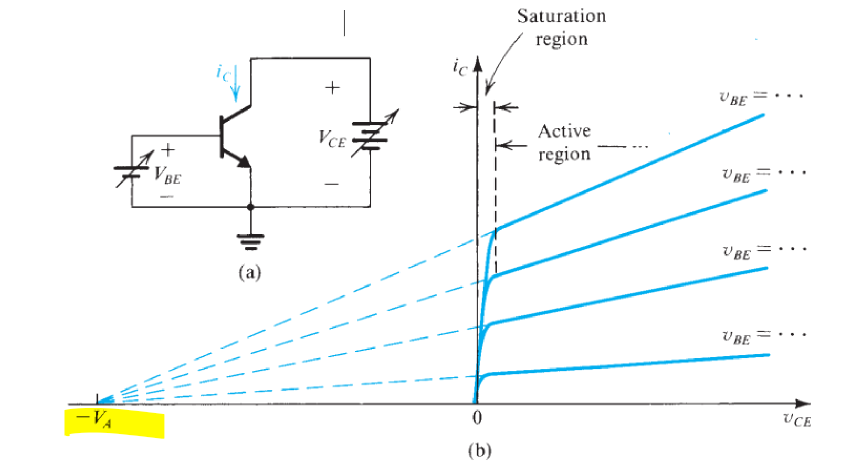
厄利效应可以等效为一个横跨在\(CE\)两极、与输出电阻\(R_C\)并联的电阻。
\[r_o=\frac{V_A}{I_C}\]
等效小信号模型
π模型
当发射极接地时,信号从基极输入。 通过对交流参数的分析,由\(r_π=\frac{v_{be}}{i_b}\),可以将基极等效为一个阻值为\(r_π\)的电阻。而由:\(i_C=g_mv_{be}=βi_b\)发射极等效为一个电流控制电压源或者\(i_b\)的电流控制电流源,得到π模型。
考虑厄利效应,有:
T模型
当基极接地时,信号从发射极输入。 由\(r_e=\frac{v_{be}}{i_e}\),可以将发射极等效为一个阻值为\(r_e\)的电阻。
由\(i_C=g_mv_{be}=αi_e\)可以将发射极等效为一个电流控制电压源或者\(i_e\)的电流控制电流源,得到T模型。
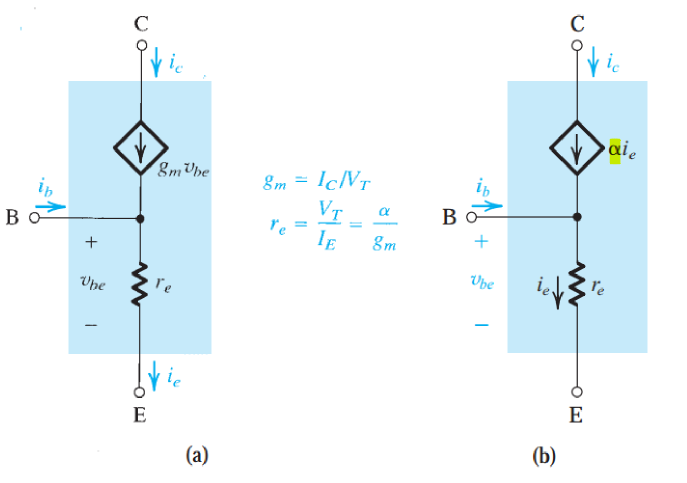
考虑厄利效应:
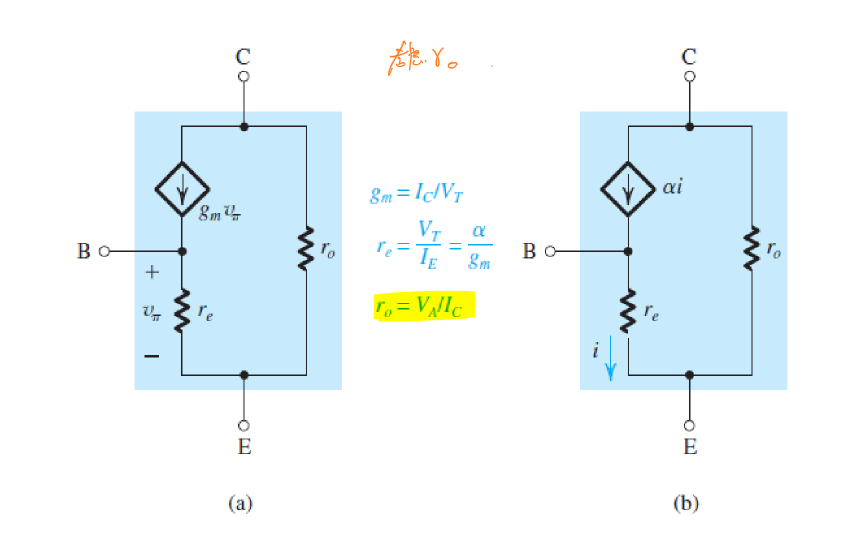
当E极在等效后没有电阻时,使用π模型进行分析。在等效后有电阻时,使用T模型进行分析。
电阻反射定律(Resistance Reflection Rule)
T模型中发射极的电阻可以通过投射定理与π模型中基极的电阻相互转换。
由于: \[r_π=r_e(β+1)\] 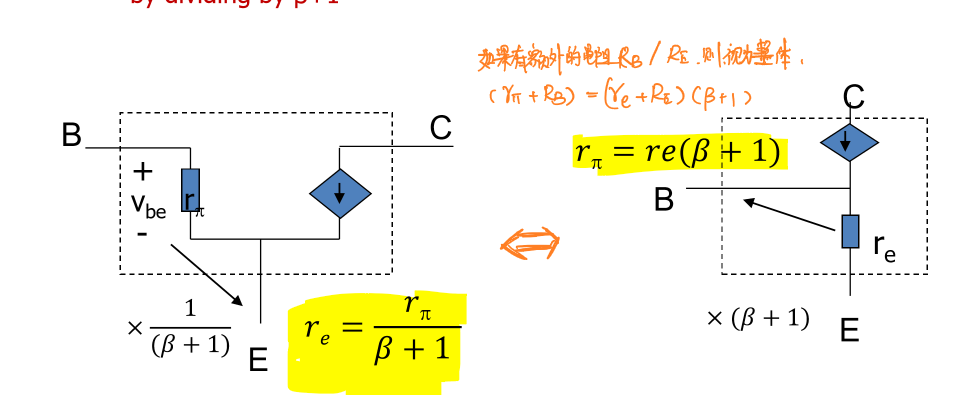
因此,发射极的所有电阻值可以乘上\(β+1\)转为基极的输入电阻的阻值。
\[R_B=(β+1)R_E\] 应用该定理可以更加灵活地判断电路中放大电路部分输入电阻的阻值。