12. 数字带通系统的调制解调方法

数字带通系统的调制解调方法

数字带通系统简述

数字带通传输系统是将数字基带信号通过载波调制，进入信道，最后在发射端解调，然后通过抽样判决器还原数字信号的过程。数字带通系统主要应用于无线传输，其结构如下图所示。

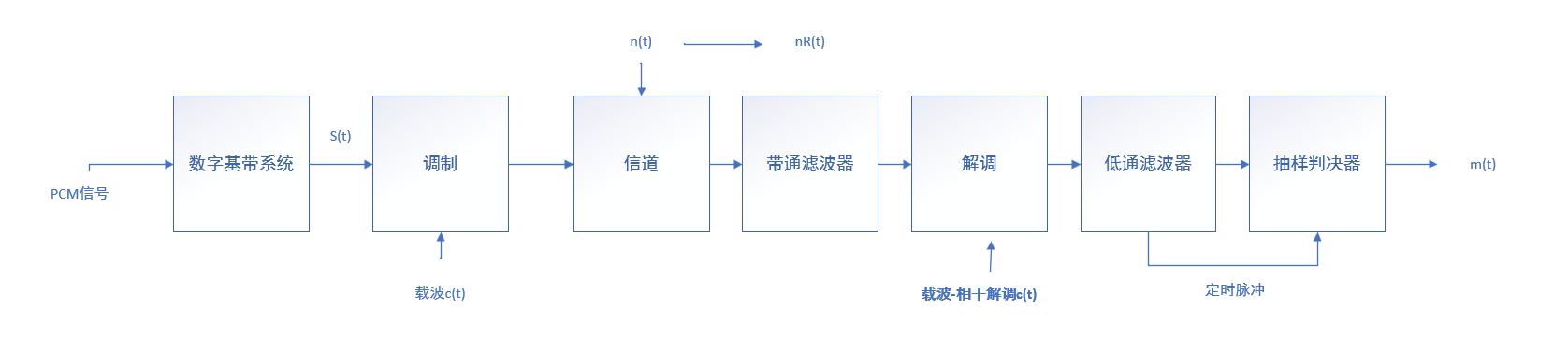
PCM信号在经过数字基带系统之后生成数字基带系统的输入信号\(S(t)\)，输入信号与载波\(c(t)\)相乘进行调制。在信道中，存在加性高斯白噪声\(n(t)\)。在接收端，经过带通滤波器后，噪声的频谱收到限制，转变为窄带噪声\(n_R(t)\)。信号进行相干解调或者非相干解调（包络检波法），通过低通滤波器过滤出高频分量，最后在抽样判决器处还原为数字信号\(m(t)\)。

2ASK

2ASK(Binary amplitude shift keying)是一种针对数字信号的调幅方法。
### 调制方法 进入调制模块的输入信号由两部分组成：周期方波脉冲信号\(g(t-nT_s)\)和需要传输的信息\(a_n=\begin{cases} 1,以概率P\\ 0,以概率1-P\\ \end{cases}\)整个信号表达为：\(S(t)=∑_na_ng(t-nT_s)\)。
该信号与载波\(cosω_ct\)相乘，得到\(S_{2ASK}(t)=[∑_na_ng(t-nT_s)]cosω_ct\)，其等价表达为：
\[S_{2ASK}(t)=\begin{cases} cosω_ct,以概率P\\ 0,以概率1-P\\ \end{cases}\]

物理实现

2ASK调制的实现有两种:
1. 模拟调制，载波和信号通过乘法器实现。
2. 键控法：原来的数字信号作为数字开关的控制信号，控制数字开关的开闭时间。数字开关的两个输入信号一个接地，即零信号，另一个输入接入载波信号\(cosω_0t\)。在原信号为“1”的时刻，数字开关打开，输出载波波形，在原信号为“0”的时刻，数字开关关闭，不输出任何信号。

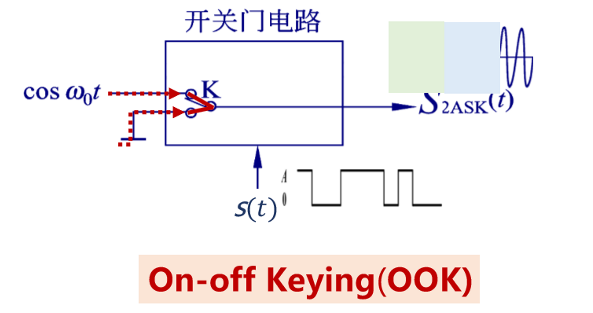
波形分析和频谱分析

整个调制过程的波形如下图所示：

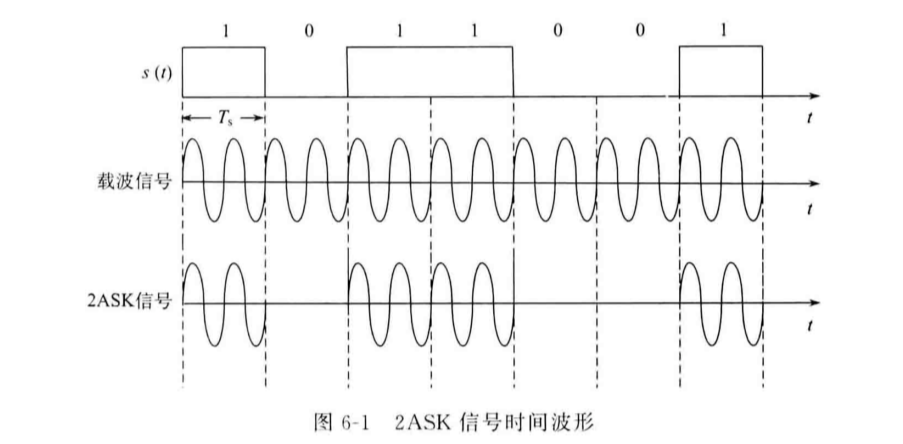
波形中每一个码元中载波的数量\(N_c\)与载波周期与码元周期之比有关：
\[N_c=\frac{T_s}{T_c}=\frac{f_s}{R_B}\] 对\(S(t)\)和载波信号的功率时间表达做傅里叶变换后相乘，得到2ASK信号的频谱表达式：
\[P_{2ASK}(f)=\frac{T_S}{16}\{Sa^2[π(f+f_c)T_s]+Sa^2[(f-f_c)T_s]\}+\frac{1}{16}[δ(f+f_c)+δ(f-f_c)]\] 其中：
- \(\frac{T_S}{16}\{Sa^2[π(f+f_c)T_s]+Sa^2[(f-f_c)T_s]\}\):连续信号，根据\(cosω_ct\)的采样性质，2ASK的频谱实际上是\(s(t)\)的频谱频域左右侧各复制一次，且幅度减半之后的结果。
- \(\frac{1}{16}[δ(f+f_c)+δ(f-f_c)]\)：离散信号，用于提取定时脉冲。

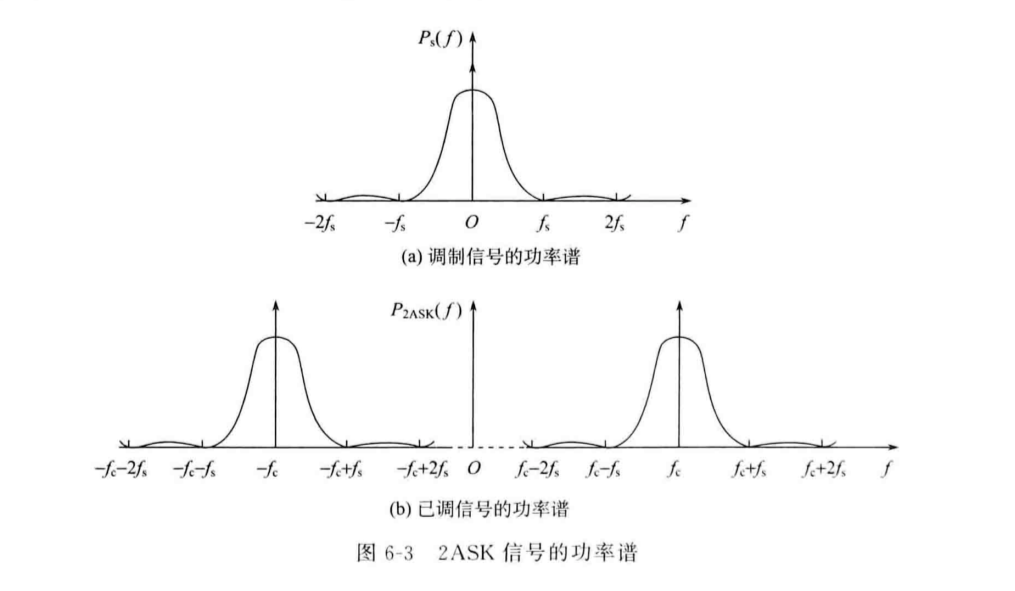
由于\(cosω_ct\)的采样性质，同时观察频谱可以得到，2ASK的频谱带宽是基带信号带宽的2倍：
\[B_{2ASK}=2B_s\] 带宽利用效率为：
\[η=\frac{R_B}{B_{2ASK}}\] 当基带信号为不归零码、没有码间串扰、且基带系统中使用理想低通滤波器时：\(B_s=2R_B=2f_s\)。
此时带宽利用效率为\(η=\frac{R_B}{B_{2ASK}}=0.5b/s.Hz\)。

解调方法

2ASK的解调可以有两种方法：相干解调和非相干解调（包络检波法）。
无论是何种解调方法，调制后的信号都要先通过带通滤波器以将高斯白噪声转换为窄带高斯白噪声，在解调模块末端，信号通过低通滤波器以除去高频分量，同时不损失原有的信息。低通滤波器的最小截止频率应当为基带信号的带宽\(ω_m\)（实际上往往采用1.5倍\(ω_m\)或者更高倍数）。

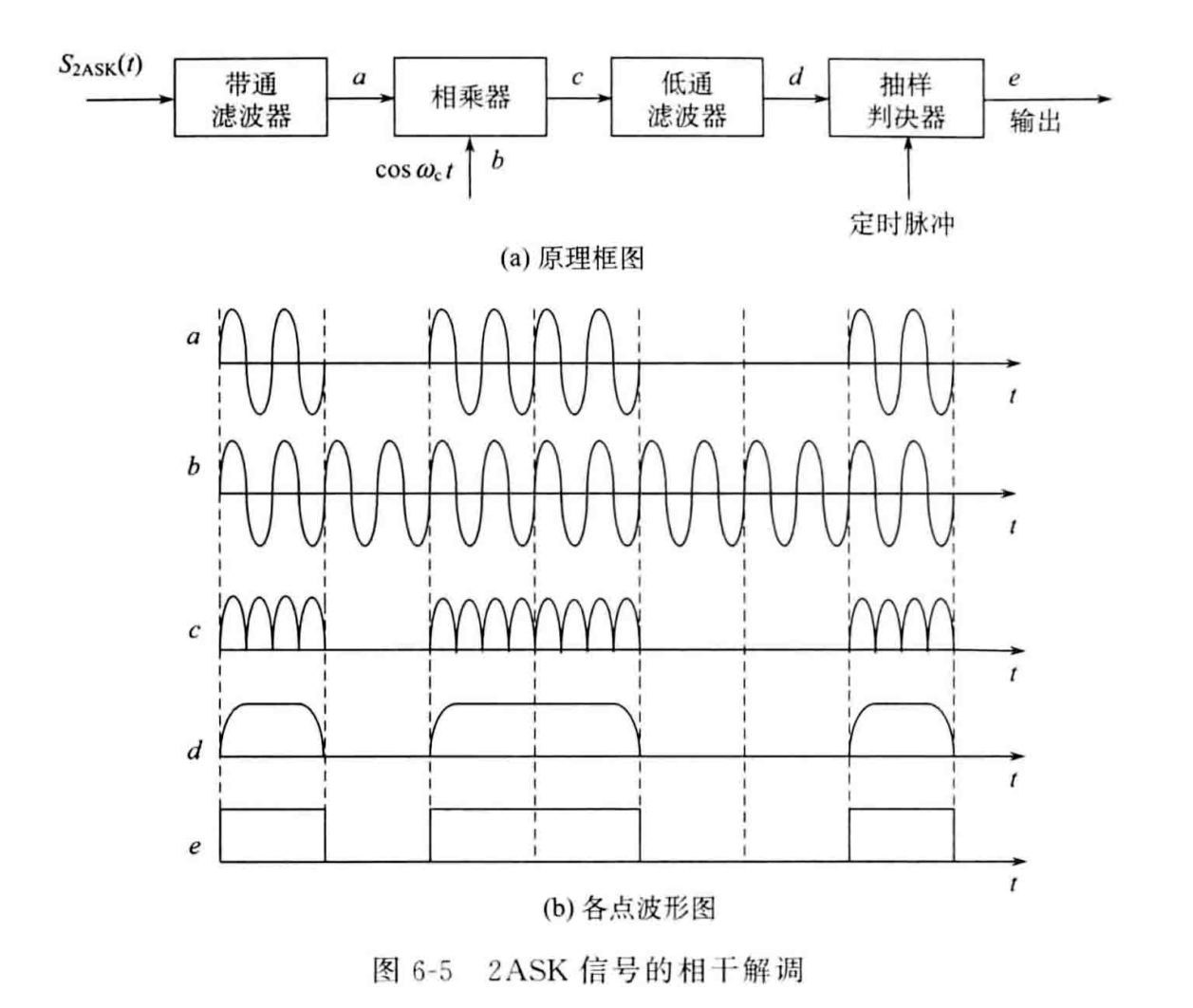
相干解调

同模拟信号调幅的解调，在接收端信号与另个同频同相的载波信号\(cosω_ct\)相乘得到：
\[S(t)cos^2ω_ct=S(t)\frac{1}{2}(1+cos2ω_ct)\] 由上述式子可以发现：
1. 在与相干波形相乘后，原信号的极性被移除。
2. 相乘后的波形由直流分量和时变波形两部分组成。

因此，使用低通滤波器只保留直流分量，最终通过抽样判决器输出数字信号。
抽样判决器的最佳判决门限应该为\(\frac{a}{2}\)。

非相干解调（包络检波法）

另一种去除信号极性的方式是使用全波整流器输出信号的绝对值波形，然后使用低通滤波器过滤高频分量，最终通过抽样判决器输出数字信号。
> 注意在模拟信号的解调中，包络检波法不需要全波整流器去除极性，注意区分。

非相干解调过程如图所示：

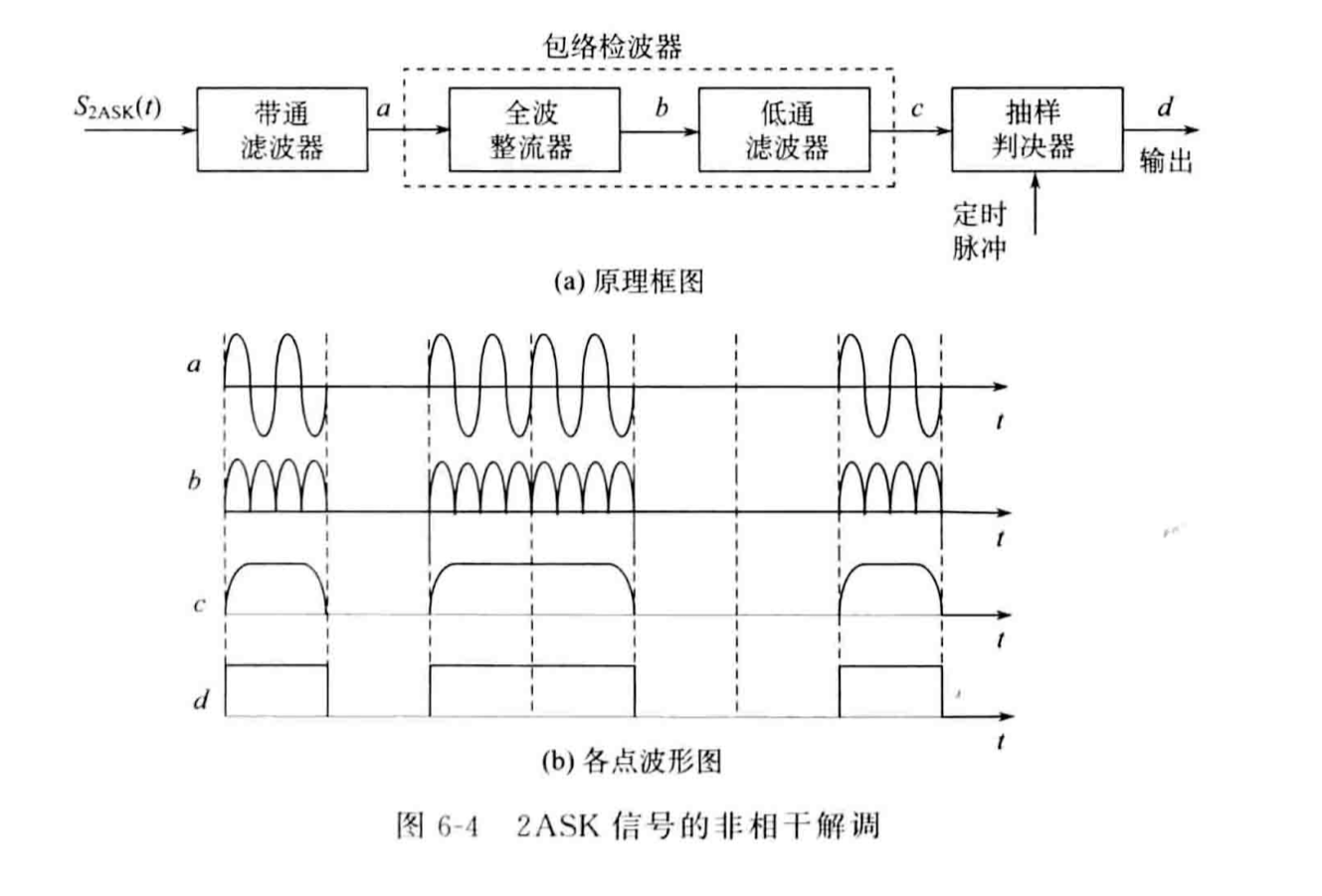
由于非相干解调中信号没有与余弦函数相乘获得余弦函数的平方，因此非相干解调输出的幅度值应当为相干解调输出信号的2倍。

由于多径传播会造成波形的振荡，影响电磁波的幅度。因此在实际通信中不会使用ASK。

FSK

调制方法

FSK使用两个不同频率的载波\(cos(ω_1t)\)、\(cos(ω_2t)\)来表示数字信号“1”和“0”。
假设原信号以\(a_n\)表示（表达式和之前的相同），\(\overline{a_n}\)表示其取反后的数字信号，那么原信号经过调制后的波形表示为：
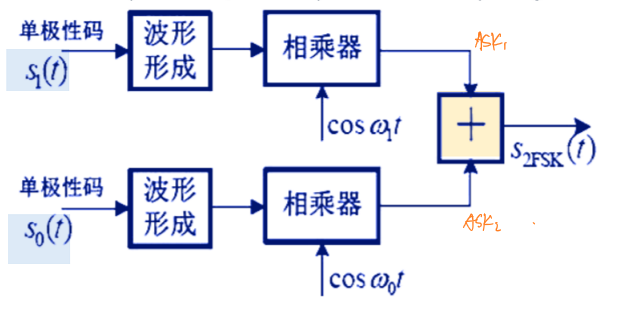
\[S_{FSK}=[∑_na_ng(t-nT_s)]cos(ω_1t)+[∑_n\overline{a_n}g(t-nT_s)]cos(ω_2t)\] 从上式可以看出FSK其实是两个频率不同的ASK信号的叠加。

物理实现

FSK调制的实现有两种:
1. 模拟调制：两个波形完全相反的信号各通过模拟调制乘上不同频率的载波后相加。

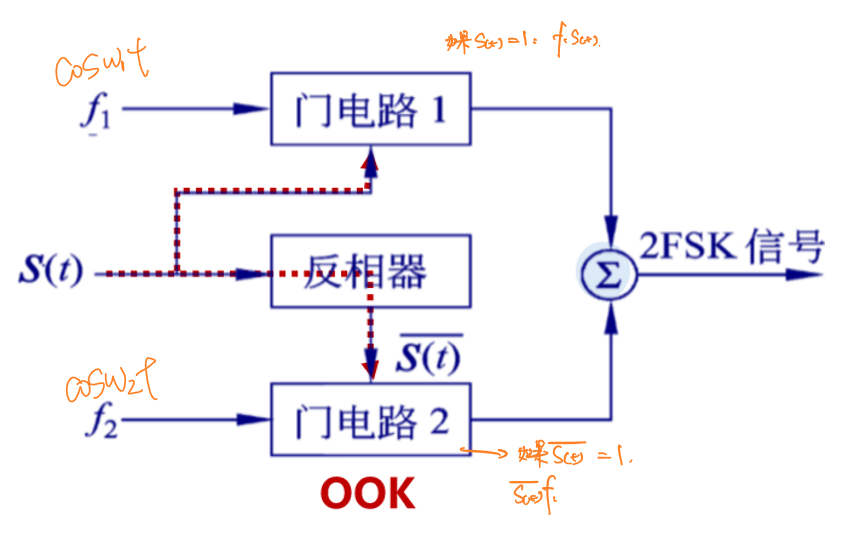
2. 键控法：原信号作为一个数字开关的控制信号的同时，其反相信号作为另一个数字开关的控制信号，两个数字开关在打开时分别输出\(cosω_1t\)与\(cosω_2t\)的波形。
   

波形和频谱分析

整个调制过程的波形如下图所示：

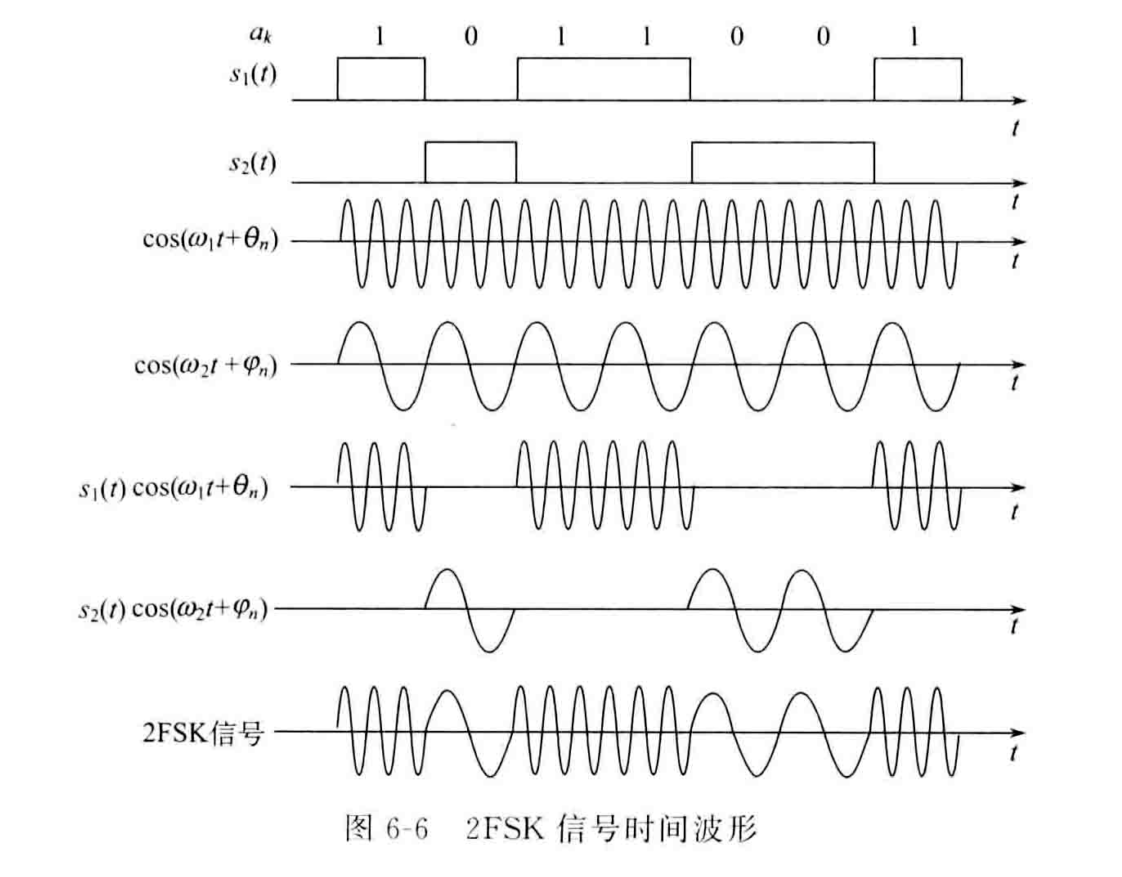
其频谱函数表达为：
\[P_{2FSK}(f)=\frac{T_s}{16}[Sa^2[π(f+f_1)T_s]+Sa^2[π(f-f_1)T_s]+Sa^2[π(f+f_2)T_s]+Sa^2[π(f-f_2)T_s]]+\frac{1}{16}[δ(f+f_1)+δ(f-f_1)+δ(f+f_2)+δ(f-f_2)]\] 其中：
- \(Sa^2[π(f+f_1)T_s]+Sa^2[π(f-f_1)T_s]\)：以\(f_1\)为中心的连续谱分量，根据\(cosω_ct\)的采样性质, 其带宽为\(B_s\)。 - \(Sa^2[π(f+f_2)T_s]+Sa^2[π(f-f_2)T_s]\)：以\(f_2\)为中心的连续谱分量,其带宽为\(B_s\)。 - \(δ(f+f_1)+δ(f-f_1)\)：以\(f_1\)为中心的冲激分量 - \(δ(f+f_2)+δ(f-f_2)\)：以\(f_2\)为中心的冲激分量

可以发现，受调信号的频谱与\(f_1\)和\(f_2\)的大小有关,当且仅当\(|f_2-f_1|≥2f_s\)时，两个连续谱分量能够完全分离。

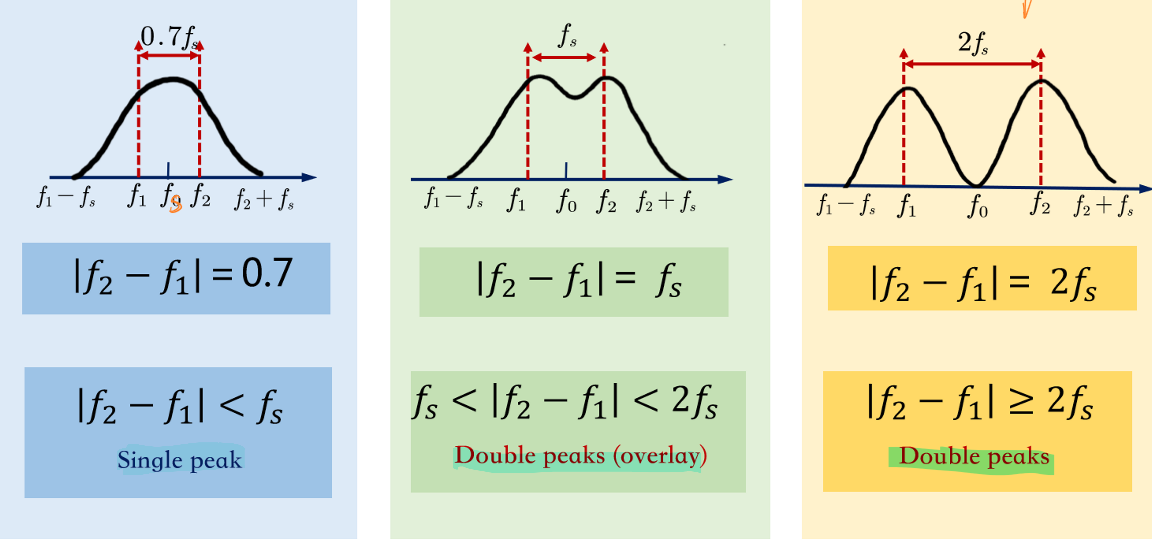
受调信号的带宽表示为：
\[B_{2FSK}=2B_S+|f_2-f_1|\]

解调方法

相干解调

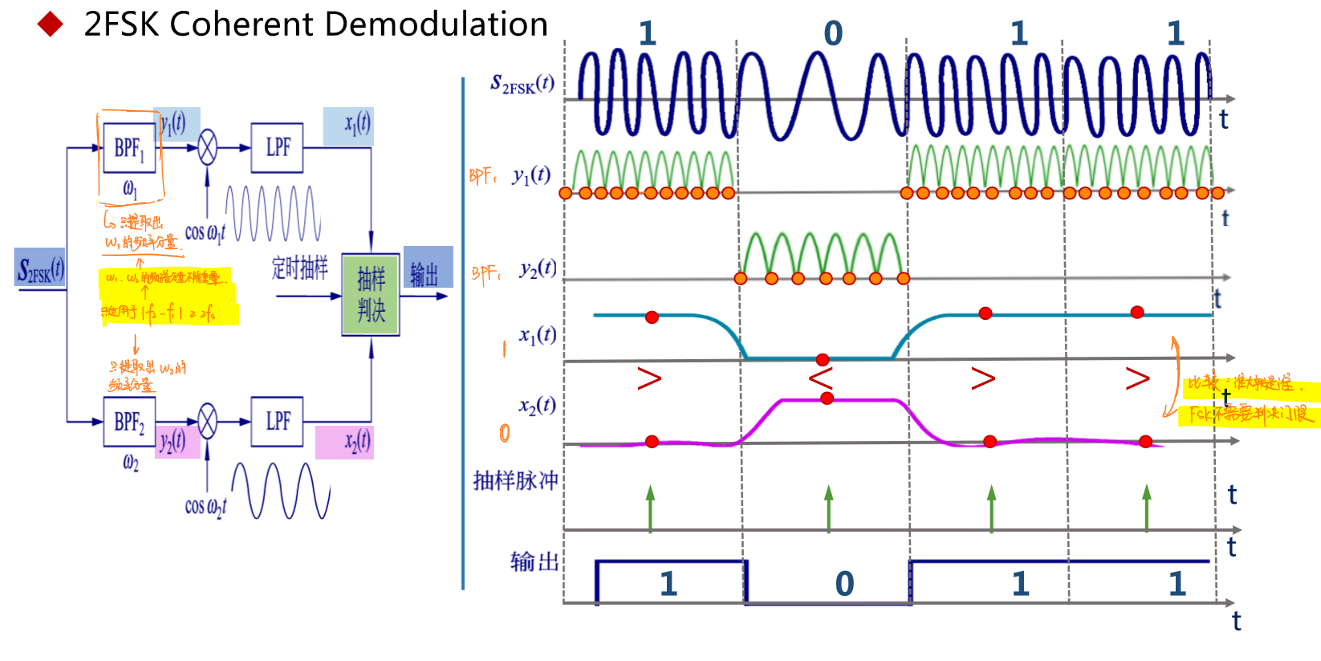
在接收端，FSK信号\(S_{2FSK}(t)\)分为两路，各通过一个带通滤波器，只过滤出\(f_1\)或者\(f_2\)的频谱分量，每一路信号在通过带通滤波器之后与对应的同频同向的载波信号相乘去除极性，通过低通滤波器过滤掉高频分量后，送入抽样判决器进行判决。
只有在\(f_1\)和\(f_2\)的连续谱分量完全分离时，带通滤波器才能准确提取出对应频率的分量，因此相干解调只适用于\(|f_1-f_2|≥2f_s\)的情况。
抽样判决器的判决标准是两路信号在同一个码元周期\(T_s\)内的电平大小进行比较，哪路信号的电平高，则数字信号的值就为这一路所代表的逻辑值。因此，相干解调不需要设置判决门限。
> 虽然对2FSK信号仍然可以通过带通滤波器提取其中一个频率的连续谱分量，使用ASK的解调方式进行解调。但是在M-FSK（即进制数不再为二进制时）信号的解调中无法单独使用某一路信号来还原全部数字信号，因此这种方法并不通用。

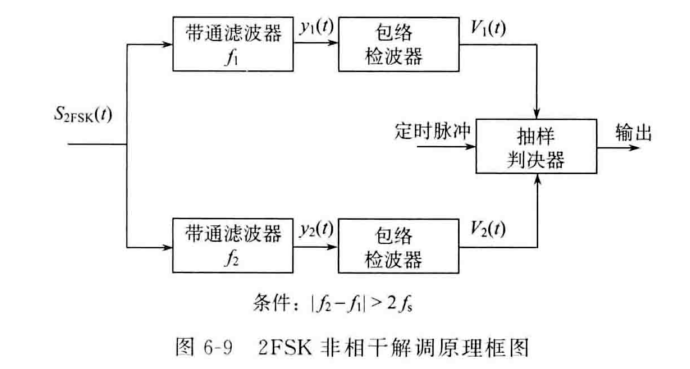
非相干解调（包络检波法）

非相干解调的过程和相干解调基本相同，只不过每一路信号采用包络检波法取代与载波相乘。
由于仍然需要带通滤波器分别提取两路信号的频谱分量，因此非相干解调也只适用于\(|f_1-f_2|≥2f_s\)的情况。
抽样判决的过程和相干解调相同，也不需要设置判决门限。

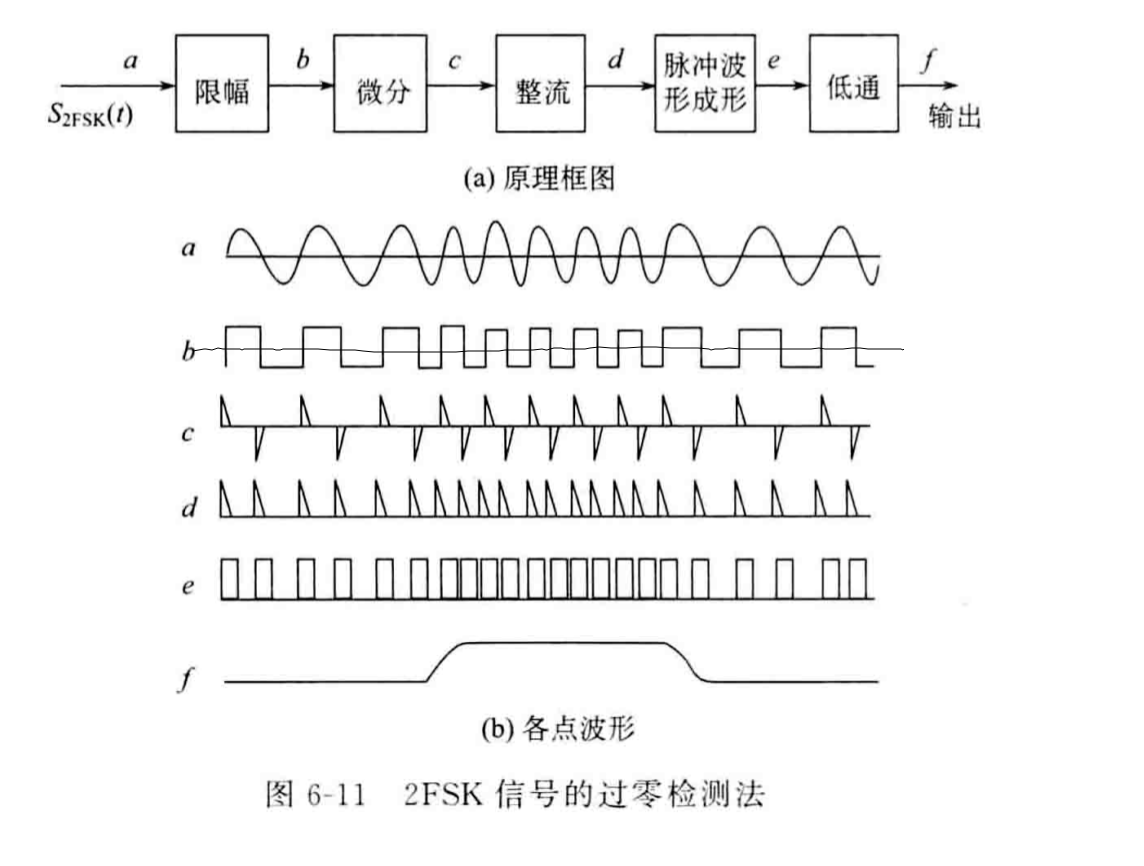
过零检波法

非相干解调和相干解调都只适用于\(|f_1-f_2|≥2f_s\)的情况，而过零检波法没有这样的条件限制。
在波形图上波形过0的次数越多代表码元周期内的频率越高，过零检波法的基本思路是用码元周期内平均幅度的大小来表示频率的高低。
过零检波法的具体过程是：FSK信号首先通过限制幅度将正弦波转变为方波，方波通过微分器后变为脉冲信号，经过整流器去除极性后，再用宽脉冲发生器依据脉冲信号重新生成无极性的方波信号。
> 宽脉冲发生器的作用是扩大码元周期之间符号持续时间的差异，这个差异在信号通过低通滤波器后会转变成直流分量幅值的差异。

方波信号会通过低通滤波器，低通滤波器只会允许低频分量（在此看做只有直流分量可以通过）通过滤波器，在单个码元周期中，方波脉冲的个数越多，代表其平均幅度越大，根据直流分量代表波形中的平均幅度可知，其直流分量也会更大。因此原波形中高频的部分通过低通滤波器之后的直流分量更大，低频部分通过低通滤波器后的直流分量更小。
> 方波脉冲信号的直流分量：\(\frac{1}{T_s}∑τ_iA_i,τ_i\)为周期内第\(i\)个方波脉冲的持续时间。

最后信号通过抽样判决器，抽样判决器的最佳判决门限为\(\frac{a}{2}\)。

PSK

调制方法

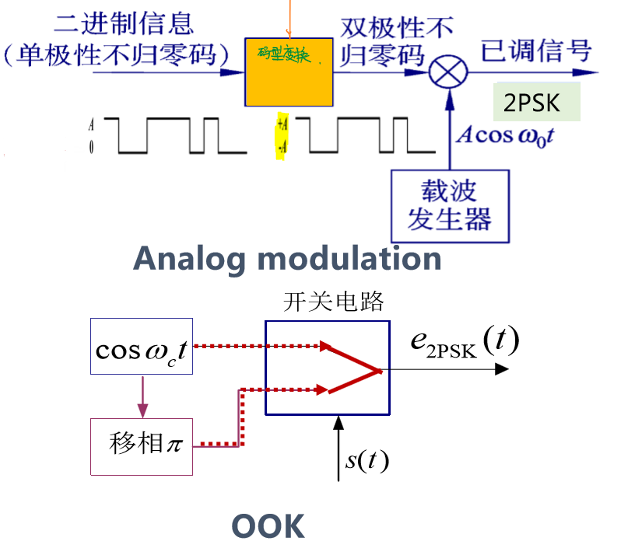
PSK对数字信号的相位进行调制，其使用两个相位不同的载波（通常相位差为\(π\)）\(Acosω_Ct\)、\(Acos(ω_ct+π)\)来表达逻辑“1”和“0”。
\[S_{2PSK}=\begin{cases} Acosω_Ct \text{ 表示"1"}\\ Acos(ω_Ct+π) \text{ 表示"0"} \end{cases}=\begin{cases} Acosω_Ct \text{ 表示"1"}\\ -Acos(ω_Ct) \text{ 表示"0"} \end{cases}\] 从表达式上可以看出，PSK将原信息\(a_n\)由单极性码转变为双极性码：\(a_n=\begin{cases} +1 \text{ 以概率P表示“1”}\\ -1 \text{ 以概率P表示“0”} \end{cases}\)，再与载波相乘。因此可以将PSK看做是双极性码的ASK。

物理实现

物理实现的方法有两种：
1. 模拟调制：将单极性码通过码型变换模块转为双极性码，再与载波相乘。
2. 键控法：数字开关的两个输入端一个为\(cosω_ct\)，其通过相移模块相移\(π\)后成为数字开关的第二个输入信号，数字开关以\(S(t)\)作为控制信号。

波形和频谱分析

PSK信号的波形可以表示为： \[S_{2PSK}(t)=∑_na_ng(t-nT_s)cosω_ct\] 其中\(a_n\)是双极性码。

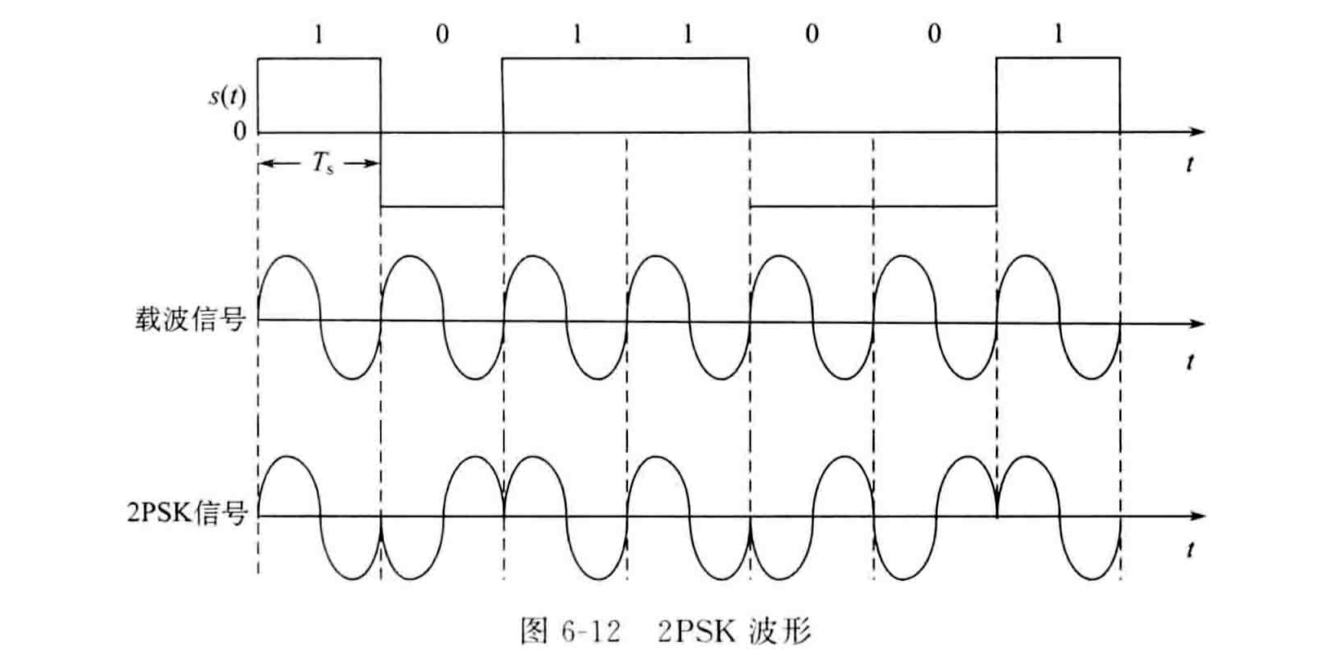
PSK的功率谱表达式为：
\[P_{2PSK}(f)=\frac{T_s}{4}\{Sa^2[π(f+f_c)T_s]+Sa^2[π(f-f_c)T_s]\}\] 可以发现，PSK的功率谱表达式实则为ASK功率谱中的连续分量。由于\(a_n\)是双极性码，因此功率谱中不含有离散的冲激分量。

PSK信号的带宽：
\[B_{2PSK}=2B_s\]

解调方法

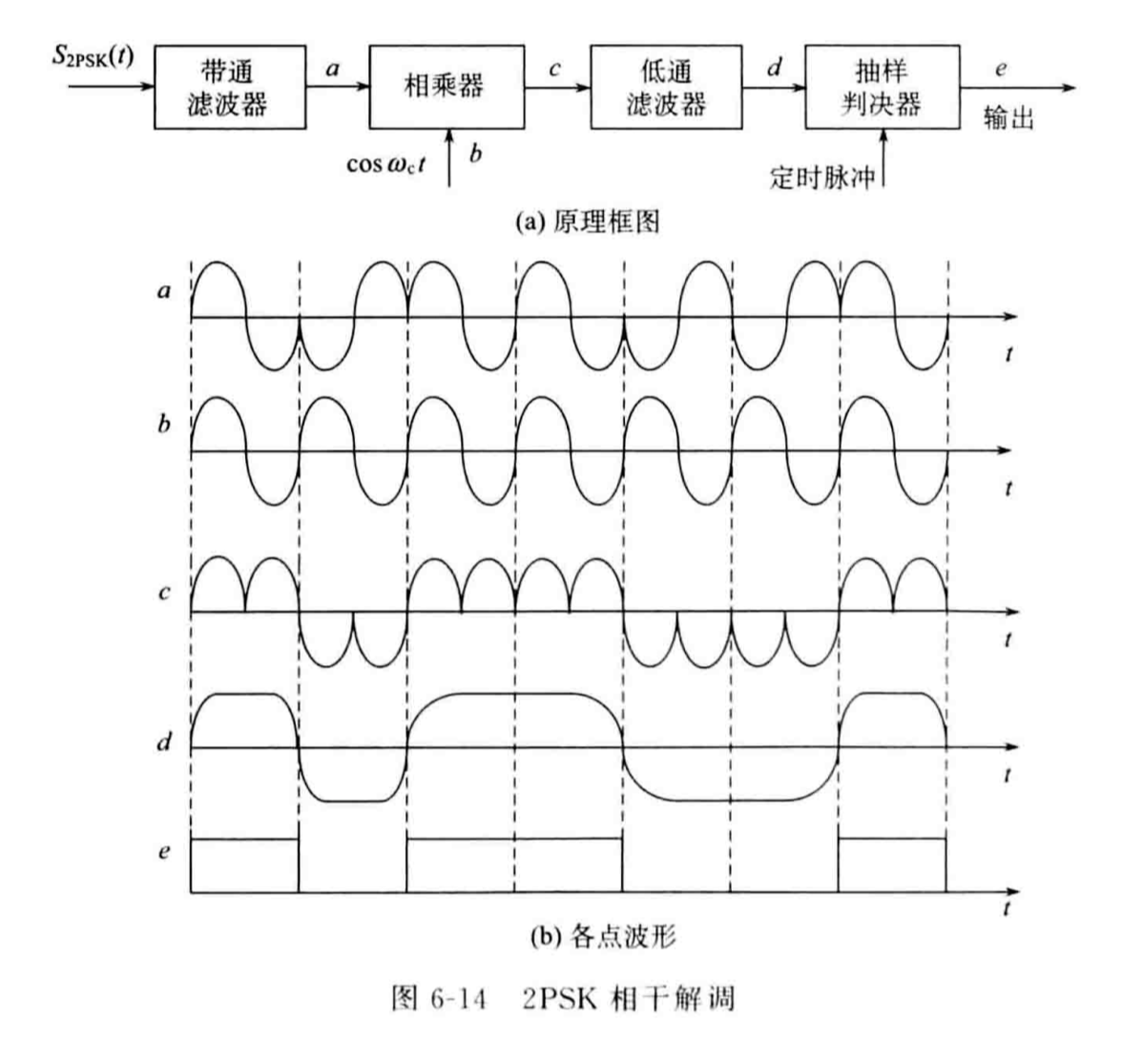
相干解调

由于PSK信号通过全波整流器后各个码元周期内的信号完全相同，无法辨认“0”或“1”，因此PSK信号不能使用非相干解调，只能使用相干解调。
在相干解调中，PSK信号通过带通滤波器后和同频同向的载波相乘，表示“-1”的波形与载波相乘，得到的波形会完全在小于0的一侧，表示“1”的波形与载波相乘，得到的波形会完全在大于0的一侧。信号通过低通滤波器消除高频分量后送入抽样判决器进行判别。抽样判决器的最佳判决门限为0。

DPSK

调制方法

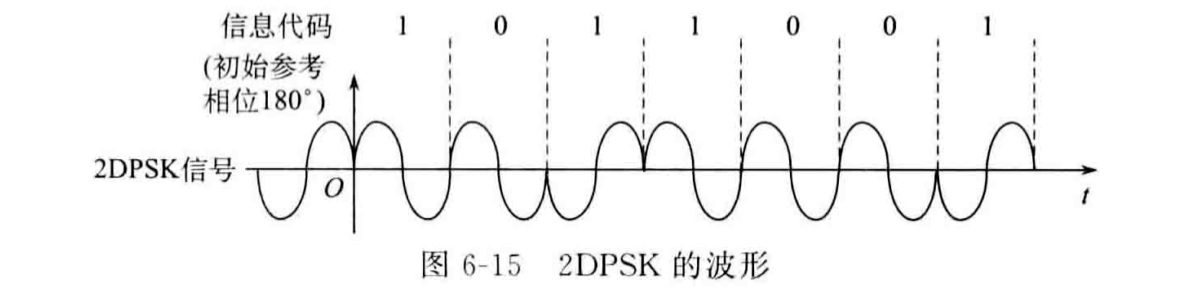
传统的PSK在解调过程中需要依赖未调制载波\(cosω_ct\)的相位，如果载波相位发生反转，调制结果会随之发生反转，这种现象称为倒π现象。为了解决倒π现象，DPSK（相对相移键控）选择使用相对码来取代PSK中使用的绝对码，以使得解调结果不依赖\(cosω_ct\)的相位。
DPSK的具体做法是:假设\(b_n\)为\(a_n\)的差分码，有： \[b_n=a_n⊕b_{n-1} \] 即当前差分码\(b_n\)是前一个差分码\(b_{n-1}\)与当前绝对码\(a_n\)的模二加法（异或）结果。
再将差分码做PSK调制即可。

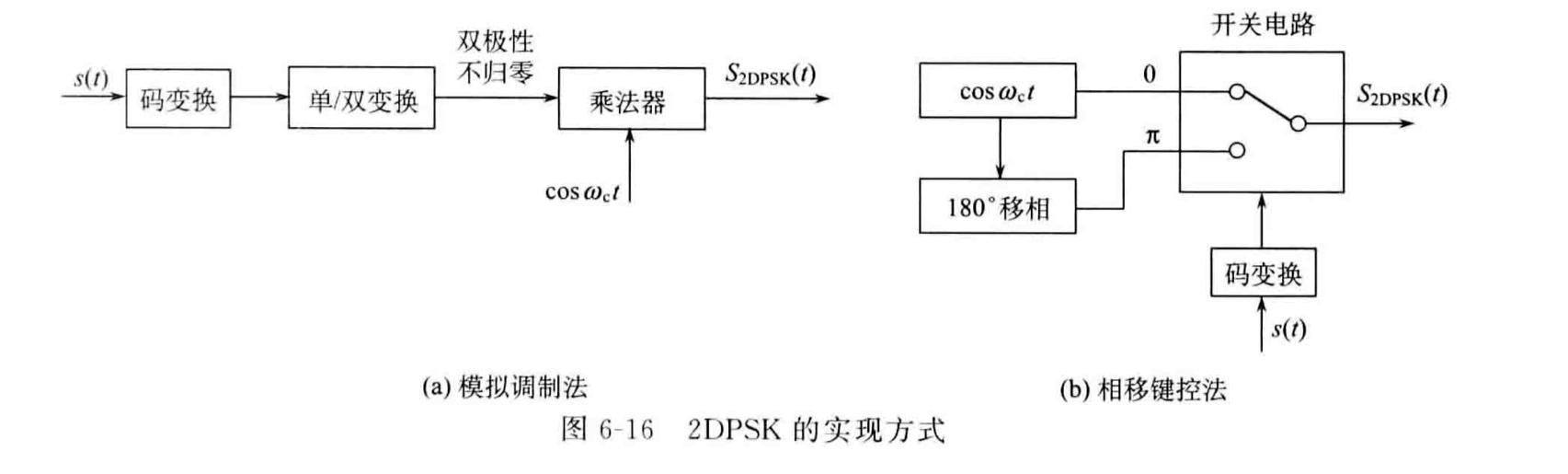
物理实现

DPSK中差分和PSK调制的顺序可以倒换：
1. 先求得码型的差分码\(b_n\)，再做PSK调制。
2. 先对码型做PSK调制，再将波形进行差分处理。
生成波形也同样可以采用键控和模拟调制两种方法。

解调方法

相干解调

同PSK相干解调

非相干解调（相位比较法/差分相干解调）

除了使用同频同相的载波与DPSK信号相乘外，还可以使用延时一个码元周期的原DPSK信号与自身信号相乘，两者都能够达到“表示-1的波形与载波相乘，得到的波形会完全在小于0的一侧，表示1的波形与载波相乘，得到的波形会完全在大于0的一侧。”的效果。

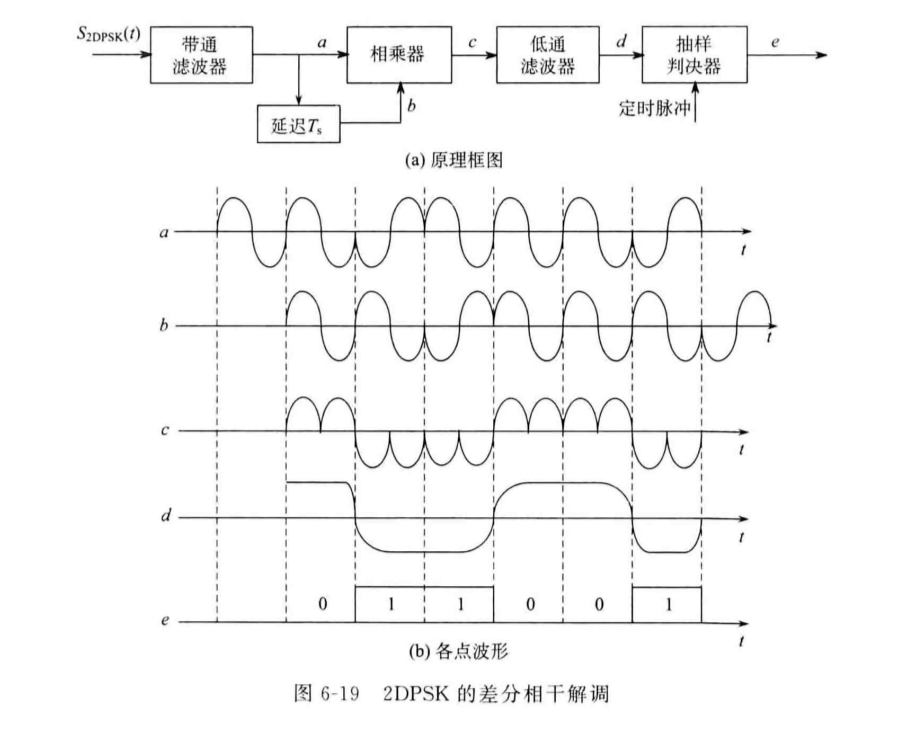
由于延迟模块比产生载波的振荡器价格更便宜，因此相位比较法在实际中的应用更为广泛。但是相位比较法的误码率高于相干解调。

调制方式	受调信号的码型	受调信号的带宽	解调方法	解调的最佳判决门限
ASK	单极性码	\(2B_s\)	相干解调 包络检波法	\(\frac{a}{2}\)
FSK	单极性码	\(\lvert f_1-f_2\rvert +2B_s\)	相干解调 包络检波法 过零检波法	无 无 \(\frac{a}{2}\)
PSK	双极性码	\(2B_s\)	相干解调	0
DPSK	双极性码	\(2B_s\)	相干解调 相位比较法	0