08. 数字滤波器的结构设计
本文最后更新于 2025年6月4日 晚上
数字滤波器的结构设计
数字滤波器设计的核心是通过给定的时域或频域系统方程,在时域设计出对应的滤波器。
数字系统的差分方程表示为:
\[∑_{k=0}^Na_ky[n-k]=∑_{k=0}^Mb_kx[n-k]\] 从中提取出\(y[n]\),并简单变换后得到关于现态输出\(y[n]\)的差分方程:
\[y[n]=\frac{1}{a_0}(∑_{k=0}^Mb_kx[n-k]-∑_{k=1}^Na_ky[n-k]),a_0≠0\] 这个方程是数字滤波器设计的主要依据。
根据加法的性质,这个差分方程中求和运算中的内部和外部的各部分可以调换计算次序,进而根据计算过程中每个部分计算次序的先后、滤波器的结构也随之不同。
滤波器设计图的画法
滤波器设计图的画法有两种:信号框图和信号流图。差分方程中的计算以加法、乘法、和时延为主,本小节也主要关注这两种画法中三种模块的表示方法。
信号框图
信号框图中加法器、乘法器和延迟器的画法如下图所示:
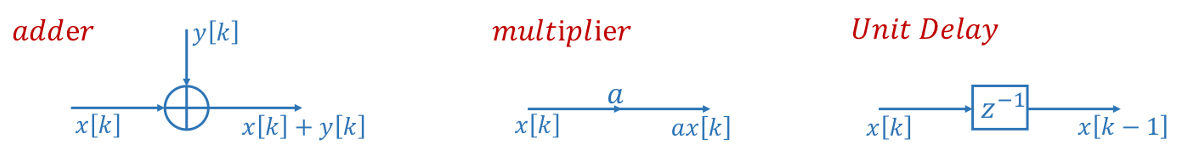
信号流图
信号流图中加法器、乘法器和延迟器的画法如下图所示:

需要注意的是,无论是信号流图还是信号框图,加法器只允许不超过两个的输入信号存在。
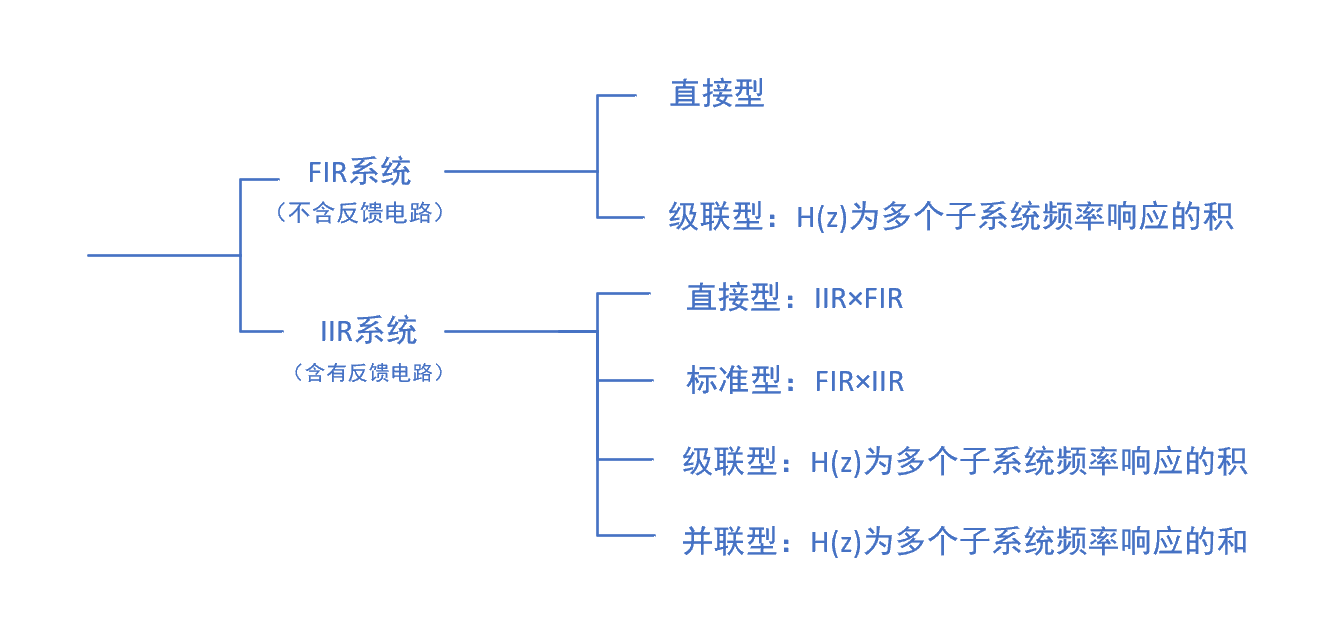
FIR系统的物理结构类型
FIR系统的差分方程由于不含有除了\(y[n]\)的其他含\(y\)项,因此FIR系统中没有反馈。FIR系统的差分方程可以写作:
\[y[n]=∑_{k=0}^Mb_kx[n-k]\] FIR系统的冲激响应即为系统差分方程的系数:
\[h[n]=\begin{cases}
b_n,0≤n≤M\\
0,otherwise\\
\end{cases}\] FIR系统的物理结构可以分为直接型(Direct form)和级联型(Cascade form)两种。
直接型
将FIR系统的差分方程中的求和直接拆开,有:
\[y[n]=b_1x[n-1]+b_2x[n-2]+..+b_Mx[n-M]\] 替换系统的冲激响应:
\[y[n]=h[1]x[n-1]+h[x][n-2]+..+h[M]x[n-M]\]
系统的直接型结构为:
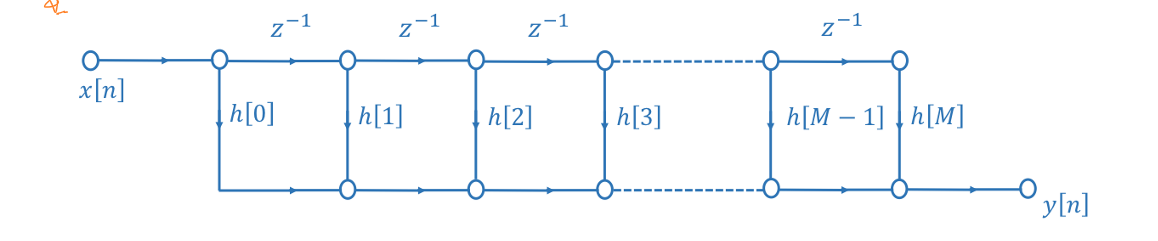
如上图所示,在直接型结构中,\(x[n]\)分别做\(M\)次时延,每一次时延后的信号与对应系数相乘后,与前面的序列相加。
硬件消耗
因此,直接型需要:
- M个时延单元(也称为存储单元,用于存放之前的输入)
- M+1个乘法单元
- M个加法单元
直接型虽然容易搭建,但是消耗器件较多。此外,由于加法器和延迟器都处于系统干路上,如果任何一个延迟器或者加法器出现故障,则整个滤波器系统将无法正常工作。
级联型
系统方程(z域)和系统的冲激响应之间存在如下关系:
\[H(z)=∑_{n=0}^Mh[n]z^{-n}\] 可以考虑构造若干个关于\(z^{-n}\)的多项式\((b_{0k}+b_{1k}z^{-1}+b_{2k}z^{-2})\),通过若干个多项式相乘构造\(∑_{n=0}^Mh[n]z^{-n}\),即:
\[H(z)=∑_{n=}^Mh[n]z^{-n}=∏_{k=1}^{M_s}(b_{0k}+b_{1k}z^{-1}+b_{2k}z^{-2})\] 其中\(M_s=[(M+1)/2]\),向下取整。\(b_{1k}\)表示第\(k\)个多项式的第1项系数,以此类推。
那么有Z域下系统输入输出关系为:
\[Y(z)=(b_{01}+b_{11}z^{-1}+b_{21}z^{-2})...(b_{0M_s}+b_{1M_s}z^{-1}+b_{2M_s}z^{-2})X(z)\] 回到时域,得到此时系统的差分方程为:
\[y[n]=(b_{01}x[n]+b_{11}x[n-1]+b_{21}x[n-2])*...*(b_{0M_s}x[n]+b_{1M_s}x[n-1]+b_{2M_s}x[n-2])\] 差分方程中卷积的实际意义是当前的节点(指某个卷积号)上携带此前所有节点的信息:
令\(w_1[n]=b_{01}x[n]+b_{11}x[n-1]+b_{21}x[n-2]\)为初始节点,有:
\[w_2=b_{02}w_1[n]+b_{12}w_1[n-1]+b_{22}w_1[n-2]\] \[w_3=b_{03}w_2[n]+b_{13}w_2[n-1]+b_{23}w_2[n-2]\] \[...\] 以此类推。
级联型结构如下图所示:
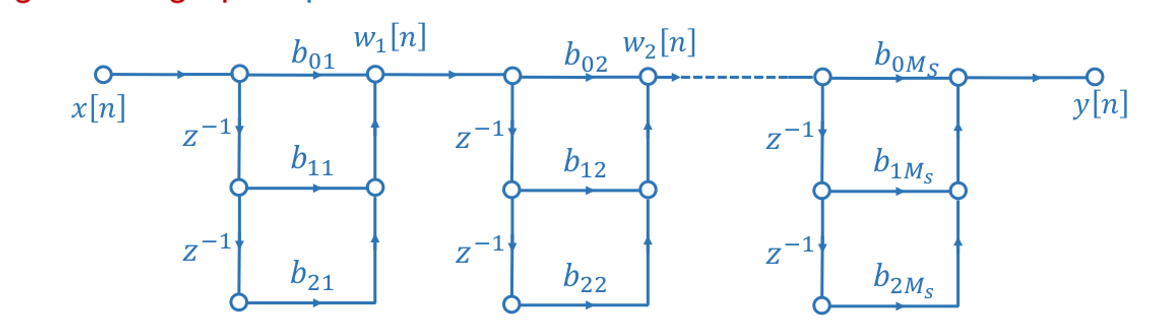
硬件消耗
在这个模块中,需要:
- M个时延单元
- \(\frac{3}{2}M\)个乘法单元
- M个加法单元
如果将\(b_0k\)做归一化处理,此时系统方程为:
\[y[n]=(1+b'_{01}x[n]+b'_{11}x[n-1]+b'_{21}x[n-2])*...*(1+b'_{0M_s}x[n]+b'_{1M_s}x[n-1]+b'_{2M_s}x[n-2])\] 那么每一个模块的第一项不再需要做乘法:
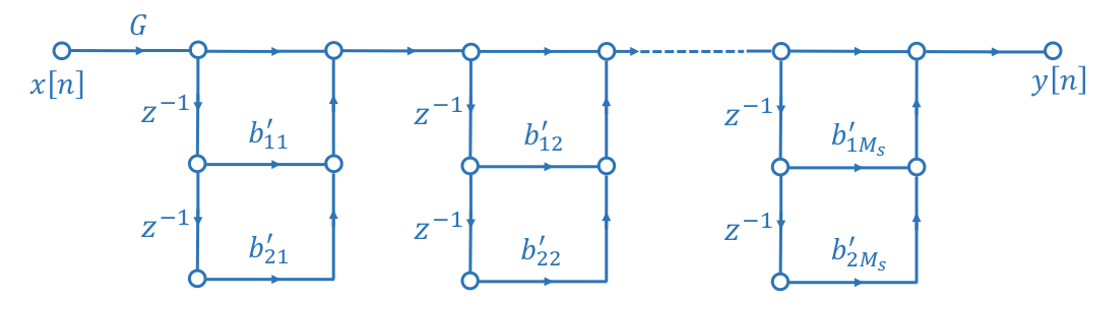
乘法单元数将减少到M+1.
该结构的优点是便于控制零点,缺点是所需系数较多,因此所需的乘法单元竖线较多。
IIR系统的物理结构类型
描述IIR系统的差分方程可以表示为:
\[y[n]=∑_{k=0}^Mb_kx[n-k]+∑_{k=1}^Na_ky[n-k]\] 描述IIR系统的差分方程中除了\(y[n]\)外还有其他的含\(y\)项,即\(y[n-m]\)。因此IIR系统的物理结构中含有反馈信号。
直接型/直接型I
描述IIR系统的差分方程在z域上可以表示为:
\[Y(z)=H(z)X(z)=(∑_{k=0}^Mb_kz^{-k})\frac{1}{1-∑_{k=1}^Na_kz^{-k}}X(z)\] 设\(H_1(z)=∑_{k=0}^Mb_kz^{-k}\),\(H_2=\frac{1}{1-∑_{k=1}^Na_kz^{-k}}\)。
可以发现\(H_1(z)\)没有极点,是FIR系统,\(H_2(z)\)是IIR系统。
在直接型I中,\(X(z)\)首先与\(H_1(z)\)结合,有:
\[V(z)=H_1(z)X(z)\] \[Y(z)=V(z)H_2(z)\] 在时域中,直接型I将系统的差分方程分解为了两部分:
\[y[n]=v[n]+∑_{k=1}^Na_ky[n-k]\] \[v[n]=∑_{k=0}^Mb_kx[n-k]\] > 可以看出\(y[n]\)是IIR系统,\(v[n]\)是一个FIR系统。
直接型I的结构如下图所示,输入信号\(x[n]\)在通过若干个延迟器后的结果赋权相加,然后将此结果与输出信号\(y[n]\)的反馈信号通过若干个延迟器后的结果赋权相加,得到现态输出\(y[n]\)的结果。
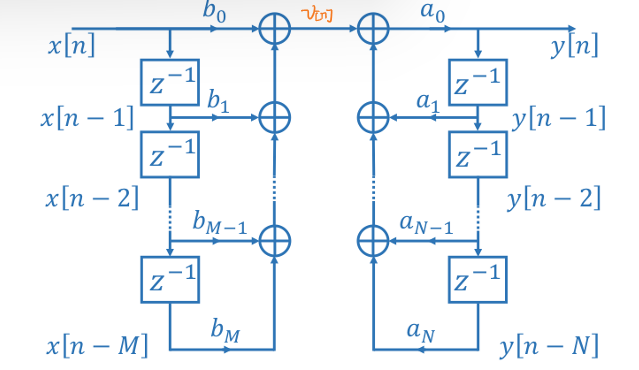
硬件消耗
直接型I需要:
- M+N个加法单元
- M+N+1个乘法单元
- M+N+1个时延单元
直接型I的优点是搭建简单,整个信号流图基本按照公式原本的样子即可搭建。缺点是所需要的硬件消耗较大。
标准型/直接型II
由, \[Y(z)=H_1(z)H_2(z)X(z)=(∑_{k=0}^Mb_kz^{-k})\frac{1}{1-∑_{k=1}^Na_kz^{-k}}X(z)\] 在直接型II中,\(X(z)\)首先与\(H_2(z)\)结合:
\[W(z)=X(z)H_2(z)\] \[Y(z)=W(z)H_1(z)\] 即 \[H(Z)=\frac{Y(Z)}{W(Z)}\frac{W(Z)}{X(Z)}\] 在时域中表示为:
\[w[n]=∑_{k=1}^Na_kw[n-k]+x[n]\] \[y[n]=∑_{k=0}^Mb_kw[n-k]\] 因此,虽然同直接型I,\(x[n]\)信号也是通过若干延迟器后赋权相加,但是此时的权重不再是\(b_N\)而应当为\(a_N\)。赋权后的信号进入另一组延迟器后赋权\(b_N\)相加。
下图表示了\(M=N\)时标准型II的结构:
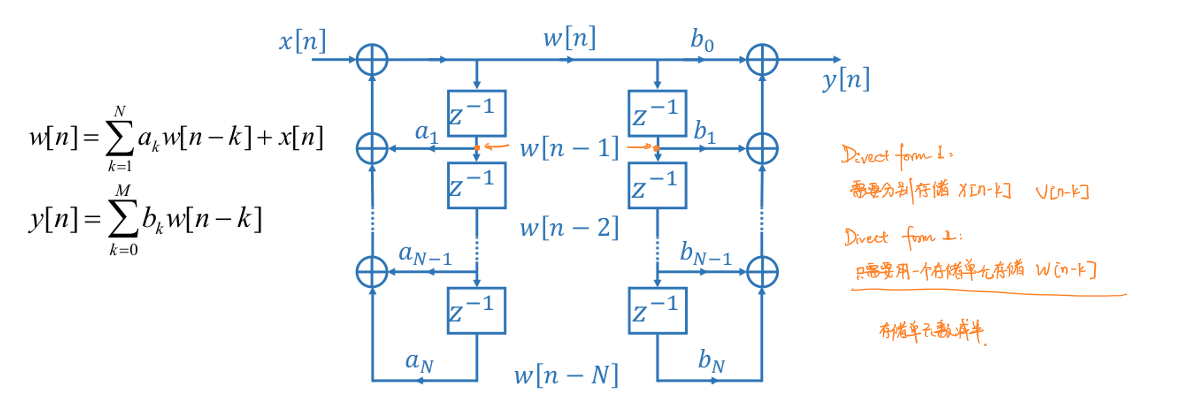
进一步化简,由于两组延迟器存储的内容都是\(w[n-k]\),因此两路信号可以共用一组延迟器,进而大幅度减小延迟器的消耗:
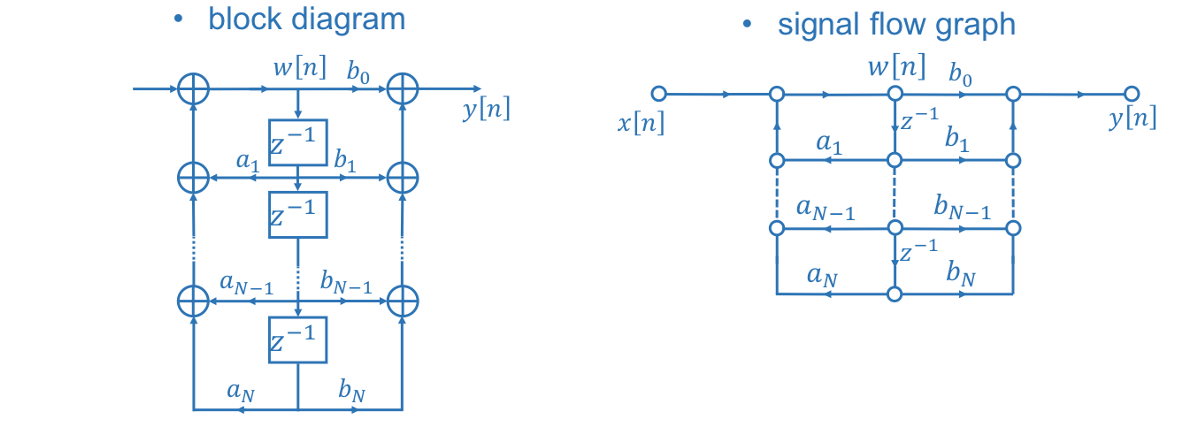
硬件消耗
直接型II需要:
- M+N个加法单元
- M+N+1个乘法单元
- max(M,N)个时延单元
相比于直接型I,直接型II大幅度减少了时延单元的消耗。
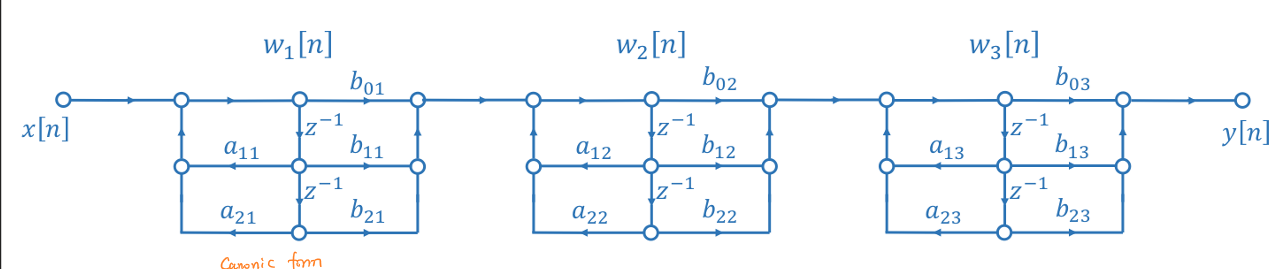
级联型
IIR系统的级联型原理与FIR系统的级联型原理相同,都是在Z域内把一个多项式分解为多个多项式的乘积。 \[H(z)=G∏_{k=1}^{N_s}\frac{1+b'_{1k}z^{-1}+b'_{2k}z^{-2}}{1-a'_{1k}z^{-1}-a'_{2k}z^{-2}}\] 其中\(N_s=\frac{N+1}{2}\) 但是IIR系统中每一个二级多项式单元\(\frac{1+b'_{1k}z^{-1}+b'_{2k}z^{-2}}{1-a'_{1k}z^{-1}-a'_{2k}z^{-2}}\)可以选择用直接型I或者直接型II实现,但是通常仍然选择使用直接型II以节省时延单元的使用个数。
级联型的结构图如下所示:
硬件消耗
当\(M=N\)时,级联型需要:
- \(4\frac{(N+1)}{2}\)个加法单元
- \(4\frac{(N+1)}{2}+1\)个乘法单元
- \(2N_s\)个时延单元
相比于直接型,级联型结构中每一个子系统单元都是独立运行的,因此系统鲁棒性优于普通型。
并联型
由z域下系统频率响应可以通过提取常数改写为:
\[H(z)=∑_{k=0}^{N_p}C_kz^{-k}+∑_{k=1}^{N_s}\frac{e_{0k}+e_{1k}z^{-1}}{1-a_{1k}z^{-1}-a_{2k}z^{-2}}\] 其中\(M≥N\)时(即\(H(z)\)是假分数时)存在第一项,\(C_k\)为常数,\(N_p=M-N\)。\(N_S=\frac{N+1}{2}\)。
由于其后的求和符号,每一个二级多项式分式都可以独立计算,从而实现并行化。
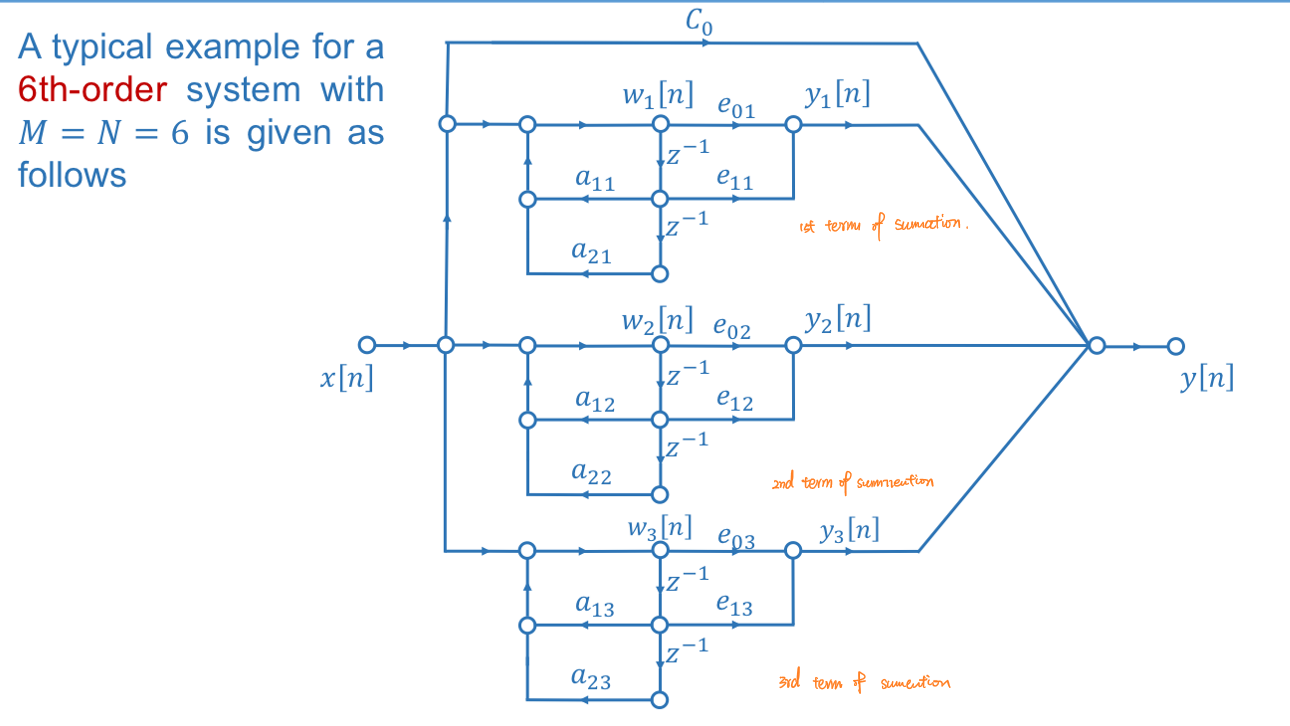
硬件消耗
当\(M=N\)时,级联型需要:
- \(4\frac{(N+1)}{2}\)个加法单元
- \(3\frac{(N+1)}{2}+1\)个乘法单元
- \(2N_s\)个时延单元
FIR和IIR的物理结构类型的特点
- 当\(h[n]\)是一个对称或者反对称序列时,直接型的计算复杂度可以被减少。
- 级联型和并联型系统的鲁棒性高于直接型。
- 相比于FIR滤波器,IIR滤波器对量化噪声更敏感。
- 级联型和并联型系统中的每一个子系统的运行情况相比于直接型更容易被观察。