09. 线性相位滤波器·FIR滤波器类型

线性相位滤波器·FIR滤波器类型

本节中需要格外注意公式的角标

线性相位滤波器

由于滤波器系统方程是一个复数函数方程，因此可以将滤波器系统方程表示为幅度和相位相乘的形式：
\[H(e^{jω})=|H(e^{jω})|e^{j∠H(e^{jω})}\] 其中\(∠H(e^{jω})\)是滤波器的相频响应(Phase Response)，\(H_r(e^{jω})=|H(e^{jω})|\)是滤波器的幅度值响应(Maganitude Response)，是幅度相应(Amplitude Response)的绝对值。
线性相位能保证信号通过系统后其中各频率成分的相对相位关系不改变，因此不容易出现在滤波器系统中因为发生码间串扰而信号失真。 线性相位滤波器的系统方程中，其相位可以表示为：
\[∠H(e^{jω})=β-αω,-π<ω<π\] 在时域上，线性相位滤波器的冲激响应具有对称性或者反对称性：
\[h[n]=h[M-1-n],0≤n≤M-1\] > 例如：\(h[n]=\{-1,2,0,2,-1\}\)

\[h[n]=-h[M-1-n],0≤n≤M-1\] > 例如：\(h[n]=\{-1,2,0,-2,1\}\)

由于线性相位系统不会改变信号相位，从而减小码间串扰的特点，在滤波器设计时基本都会保证滤波器是线性相位的。

FIR 滤波器的优点

FIR滤波器的系统方程可以由：
\[H(z)=∑_{n=N_1}^{N_2}h[n]z^{-n}\]

FIR 滤波器具有以下主要优点： - 它们可以具有精确的线性相位。 - 由于\(∑_{k=N_1}^{N_2}|h[n]|<∞\)，它们始终稳定。 - 设计方法通常是线性的。 - 它们可以在硬件中高效实现。

FIR 滤波器的主要缺点是，要达到同样的性能水平，其所需阶数远高于 IIR 滤波器。相应地，这些滤波器的延迟通常比同等性能的 IIR 滤波器大得多。

最重要的原因是FIR滤波器是线性相位滤波器，因此实际设计中，通常更倾向于设计FIR滤波器。

线性相位FIR滤波器的类型

按照系统方程的冲激响应序列是对称/反对称的，以及整个序列的长度\(M\)的奇偶性，可以将线性相位的FIR滤波器分为四类。下面来求这四种系统类型的相频响应。

第一类：冲激响应对称、序列长度为奇数

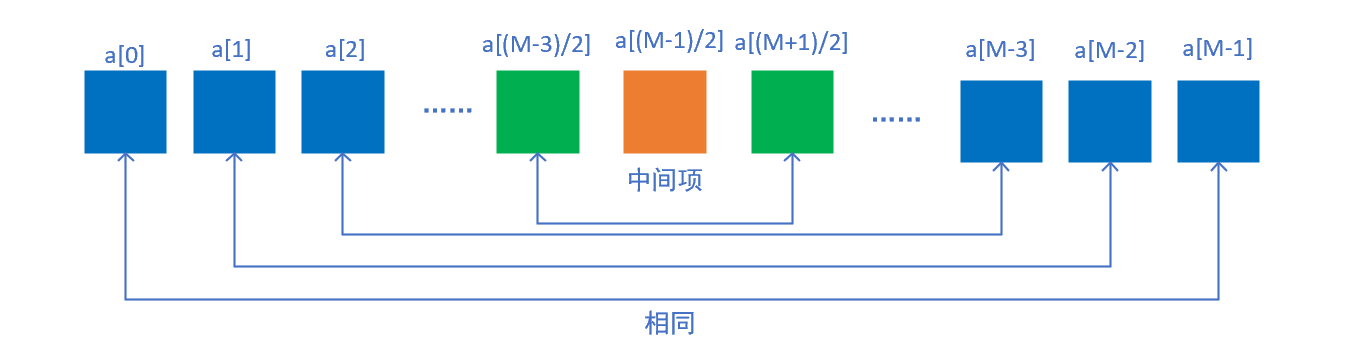
此时的冲激响应表示为：
\[h[n]=h[M-1-n],\frac{M-1}{2}\text{是整数。}\] 由于序列中以中间项为分割线，前一半序列和后一半序列完全相同。 那么系统的频率响应序列可以表示为：前一半序列的离散时间傅里叶变换的二倍与中间项的离散时间傅里叶变换之和：
\[\begin{aligned} H(e^{jω})&=∑_{n=0}^{M-1}h(n)e^{-jωn}\\ &=∑_{n=0}^{(M-3)/2}h(n)e^{-jωn}+h(\frac{M-1}{2})e^{-j(M-1)ω/2}+∑_{n=(M+1)/2}^{M-1}h(n)e^{-jωn}\\ \end{aligned}\] 对于每一个对称项，有：
\[h(0+n)e^{-jω(0+n)}+h(\frac{M-1}{2}-n)e^{-jω(\frac{M-1}{2}-n)}=2h(\frac{M-1}{2})cos(ωn)\] 令：\(a[n]=2h[\frac{M-1}{2}-n]\)，带入\(a[n]\)，得到：
\[H(e^{jω})=\left(∑_{n=0}^{(M-1)/2}a[n]cos(ωn)\right)e^{-jω(M-1)/2}\] 根据上述式子可以得到其相频响应为：
\[∠H(e^{jω})=-\frac{(M-1)ω}{2}\] 即\(β=0\),\(α=\frac{M-1}{2}\)。

第二类：冲激响应对称、序列长度为偶数

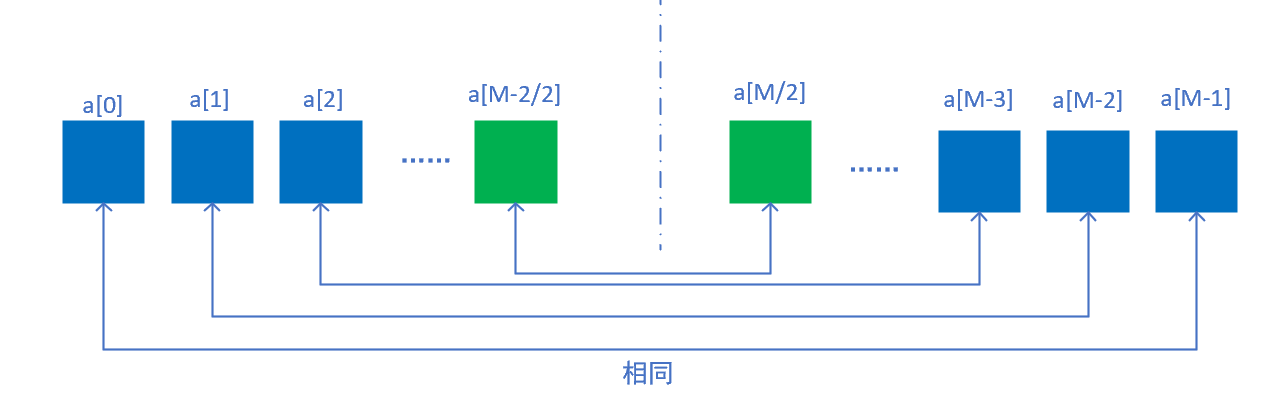
此时的冲激响应表示为：
\[h[n]=h[M-1-n],\frac{M-1}{2}\text{非整数。}\] 由于不存在中间项，相比于第一类，其系统方程中不存在中间项：
\[\begin{aligned} H(e^{jω})&=∑_{n=0}^{M-1}h(n)e^{-jωn}\\ &=∑_{n=0}^{(M-2)/2}h(n)e^{-jωn}+∑_{n=M/2}^{M-1}h(n)e^{-jωn}\\ \end{aligned}\] 将序列改写，并把相同项进行合并，注意前半部分和后半部分对应项的奇偶性正好相反：
\[b[n]=2h[\frac{M}{2}-n]\] 同理运用欧拉公式可得：
\[H(e^{jω})=\left(∑_{n=0}^{M/2}b[n]cos(ω(n-\frac{1}{2}))\right)e^{-jω(M-1)/2}\] 其相频响应为：
\[∠H(e^{jω})=-\frac{(M-1)ω}{2}\] 即\(β=0\),\(α=\frac{M-1}{2}\)。

第三类：冲激响应反对称、序列长度为奇数

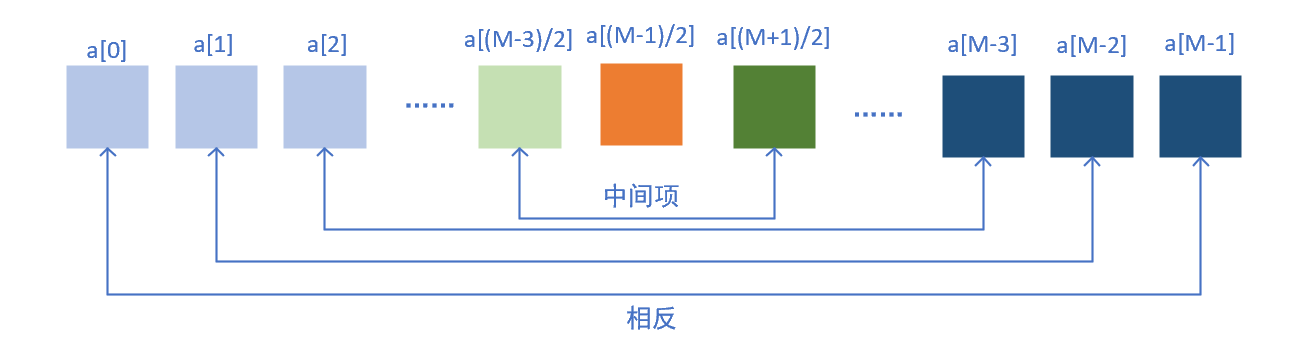
同理可得其系统方程的化简结果为：
\[H(e^{jω})=\left(\sum_{n=1}^{(M-1)/2}c[n]sin(ωn)\right)e^{j[\frac{π}{2}-\frac{ω(M-1)}{2}]}\] \[c[n]=2h[\frac{M-1}{2}-n]\] 其相频响应为：
\[∠H(e^{jω})=\frac{π}{2}-\frac{(M-1)ω}{2}\] 即\(β=\frac{π}{2}\),\(α=\frac{M-1}{2}\)。

第四类：冲激响应反对称、序列长度为偶数

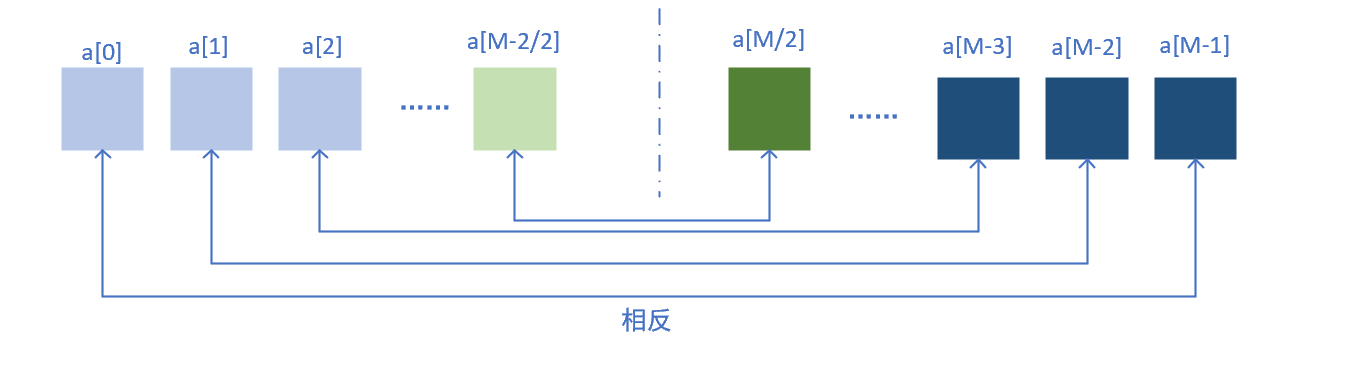
同理可得其系统方程的化简结果为：
\[H(e^{jω})=\left(\sum_{n=1}^{M/2}d[n]sin(ω(n-\frac{1}{2}))\right)e^{j[\frac{π}{2}-\frac{ω(M-1)}{2}]}\] \[d[n]=\frac{M-1}{2}\] 其相频响应为：
\[∠H(e^{jω})=\frac{π}{2}-\frac{(M-1)ω}{2}\] 即\(β=\frac{π}{2}\),\(α=\frac{M-1}{2}\)。