13. 数字带通系统的抗噪性分析

数字带通系统的抗噪性分析

ASK的抗噪性分析

在调制端，输入信号可以由ASK信号和窄带高斯白噪声组成：
\[y_i(t)=u_i(t)+n_i(t)\] 其中:\(u_i(t)=\begin{cases} acosω_ct,表示“1”\\ 0, 表示“0” \end{cases}\) 输入噪声可以通过正交分解表示为: \(n_i(t)=n_c(t)cosω_ct-n_s(t)sinω_ct\)。

那么通过带通滤波器后的信号：
\[y(t)=\begin{cases} [a+n_c(t)]cosω_ct-n_ssinω_ct,\text{ 表示“1”}\\ n_c(t)cosω_ct-n_s(t)sinω_ct,\text{ 表示“0”} \end{cases}\]

相干调制的误码率分析

在相干调制中，信号与载波信号相乘得到：
\[z(t)=y(t)cosω_ct=\begin{cases} [a+n_c(t)]cos^2ω_ct-n_ssinω_ctcosω_ct,\text{ 表示“1”}\\ n_c(t)cos^2ω_ct-n_s(t)sinω_ctcosω_ct,\text{ 表示“0”} \end{cases}\] 其中，由于低通滤波器只允许低频分量和直流分量通过，在无线传输中，一般认为载波频率很高，因此含有\(t\)的所有项无法通过滤波器，最终得到：
\[x(t)=\begin{cases} \frac{1}{2}[a+n_c(t)],\text{ 表示“1”}\\ \frac{1}{2}n_c(t),\text{ 表示“0”} \end{cases}\] 其中幅值\(\frac{1}{2}\)可以通过放大器消除。
同数字基带系统的抗噪性分析，计算码元为“0”时判别为“1”的概率和码元为“1”时判别为“0”的概率，得到在\(P(0)=P(1)=0.5\)时的误码率：
\[P_e=\frac{1}{2}erfc(\frac{\sqrt{SNR}}{2})\]

非相干信号的误码率分析

通过带通滤波器的信号进行包络检波：
\[V(t)=\begin{cases} \sqrt{([a+n_c(t)]^2+n_s^2(t))},\text{ 表示“1”}\\ \sqrt{(n_c^2(t)+n_s^2(t))}, \text{ 表示“0”}\\ \end{cases}\] 通过计算得到：
\[P_e=\frac{1}{2}e^{-\frac{SNR}{4}}=\frac{1}{2}e^{-\frac{SNR}{4}}\]

ASK信号的信噪比

对于ASK信号，信噪比为：
\[SNR_{ASK}=\frac{\frac{a^2}{2}}{n_0B_{ASK}}=\frac{\frac{a^2}{2}}{2n_0B_s}\]

FSK的抗噪性分析

FSK信号的误码率

FSK信号的误码率可以表示为：
采用相干解调时：
\[P_e=\frac{1}{2}erfc(\sqrt{\frac{SNR_{FSK}}{2}})\] 采用非相干解调时：
\[P_e=\frac{1}{2}e^{-\frac{SNR_{FSK}}{2}}\]

FSK信号的信噪比

FSK信号的解调过程实际上是两路信号做ASK解调，因此：
\[SNR_{FSK}=\frac{\frac{a^2}{2}}{n_0B_{ASK}}=\frac{\frac{a^2}{2}}{2n_0B_{S}}\]

PSK信号的抗噪性分析

PSK信号的误码率

PSK信号的误码率可以表示为：
采用相干解调时：
\[P_e=\frac{1}{2}erfc(\sqrt{SNR_{PSK}})\] 采用差分解调时：
\[P_e=\frac{1}{2}e^{-SNR_{PSK}}\]

PSK信号的信噪比

PSK信号的信噪比和ASK信号相同：
\[SNR_{PSK}=\frac{\frac{a^2}{2}}{n_0B_{PSK}}=\frac{\frac{a^2}{2}}{2n_0B_{S}}\]

ASK/FSK/PSK抗噪性比较

通过公式得出ASK/FSK/PSK抗噪性、采用相干/非相干解调方法时的抗噪性曲线：

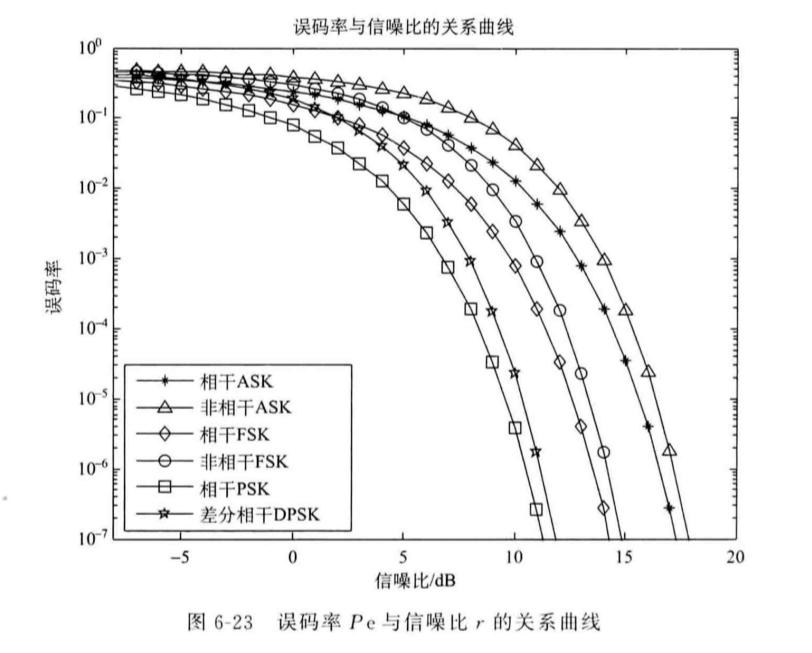
可以从上图总结出如下结论：
1. 抗噪性：PSK>DPSK>FSK>ASK 2. 抗噪性： 相干解调>非相干解调
3. 系统的误码率下降时，系统的信噪比上升。

此外，ASK/PSK和DPSK的带宽相同，FSK的带宽大于前三者，因此FSK的频谱利用效率最低。

使用MATLAB©绘制ASK/FSK/PSK的BER-SNR曲线

使用linspace()函数创建一个从-10到30的等差数列，公差为10，用于描述分贝表示的SNR：r_dB = linspace(-10,10,30);，然后将SNR转换为数值描述： r = 10.^(r_dB/10);。 在MATLAB中使用erfc()函数即可得到互补误差函数在特定点下的输出。那么ASK/PSK/DPSK/FSK在相干解调/非相干解调下的误码率可以表示为：

ask_co = 0.5.*erfc(sqrt(r)/2);
ask_no = 0.5.*exp(-r/4);
fsk_co = 0.5.*erfc(sqrt(r/2));
fsk_no = 0.5.*exp(-r/2);
psk_co = 0.5.*erfc(sqrt(r));
dpsk = 0.5.*exp(-r);

使用函数semilogy()绘制出y轴以10的次方表示的折线图。
完整的例程如下：

r_dB = linspace(-10,10,30); %创建SNR
r = 10.^(r_dB/10); %转换为数值描述

% 表示BER
ask_co = 0.5.*erfc(sqrt(r)/2);
ask_no = 0.5.*exp(-r/4);
fsk_co = 0.5.*erfc(sqrt(r/2));
fsk_no = 0.5.*exp(-r/2);
psk_co = 0.5.*erfc(sqrt(r));
dpsk = 0.5.*exp(-r);

% 绘图
semilogy(r_dB,ask_co,'r','DisplayName','ASK coherent demodulation')
hold on
semilogy(r_dB,ask_no,'b','DisplayName','ASK none-coherent demodulation')
semilogy(r_dB,fsk_no,'g','DisplayName','FSK none-coherent demodulation')
semilogy(r_dB,fsk_co,'w','DisplayName','FSK coherent demodulation')
semilogy(r_dB,psk_co,'k','DisplayName','PSK coherent demodulation')
semilogy(r_dB,dpsk,'m','DisplayName','DPSK differential demodulation')
xlabel('SNR(dB)')
ylabel('BER')
grid on
hold off

总结：ASK/FSK/PSK的参数性能

ASK是一种应用最早的基本调制方式。其优点是设备简单，频带利用率较高；缺点是抗噪声性能差，并且对信道特性变化敏感，不易是抽样判决器工作在最佳判决门限状态。
FSK是数字通信中不可或缺的一种调制方式。其优点是抗干扰能力较强，不受信道参数变化的影响，因此FSK特别适合应用于衰落信道；缺点是占用频带较宽，尤其是MFSK，频带利用率较低。目前，调频体制主要应用于中，低速数据传输与接入中。
PSK和DPSK是一种高传输效率的调制方式，其抗噪声能力比ASK和FSK都强，且不易受信道特性变化的影响，因此在高、中速数据传输中得到了广泛的应用。绝对相移（PSK）在相干解调时存在载波相位模糊的问题，在实际中很少采用于直接传输，MDPSK应用更为广泛。

调制方式	受调信号的码型	受调信号的带宽	解调方法	解调的最佳判决门限	最大频谱利用效率	误码率
ASK	单极性码	\(2B_s\)	相干解调 包络检波法	\(\frac{a}{2}\)	\(\frac{1}{2}\)	\(\frac{1}{2}erfc(\frac{\sqrt{SNR}}{2})\) \(\frac{1}{2}e^{-\frac{SNR}{4}}\)
FSK	单极性码	\(\lvert f_1-f_2\rvert +2B_s\)	相干解调 包络检波法 过零检波法	无 无 \(\frac{a}{2}\)	\(\frac{R_B}{\lvert f_1-f_2\rvert +2R_B}\)	\(\frac{1}{2}erfc(\sqrt{\frac{SNR_{FSK}}{2}})\) \(\frac{1}{2}e^{-\frac{SNR_{FSK}}{2}}\)
PSK	双极性码	\(2B_s\)	相干解调	0	\(\frac{1}{2}\)	\(\frac{1}{2}erfc(\sqrt{SNR_{PSK}})\)
DPSK	双极性码	\(2B_s\)	相干解调 相位比较法	0	\(\frac{1}{2}\)	\(\frac{1}{2}e^{-SNR_{PSK}}\)

所有调制方法的信噪比均为： \(SNR=\frac{\frac{a^2}{2}}{2n_0B_{S}}\)。