09. 晶体管单级放大电路

晶体管单级放大电路

集成电路中的运算放大器是由晶体管组成的，最基本的三种用晶体管构成的单级放大电路为：

• 共射极放大电路(Common Emitter)
• 共基极放大电路(Common Base)
• 共集极放大电路(Common Collector)

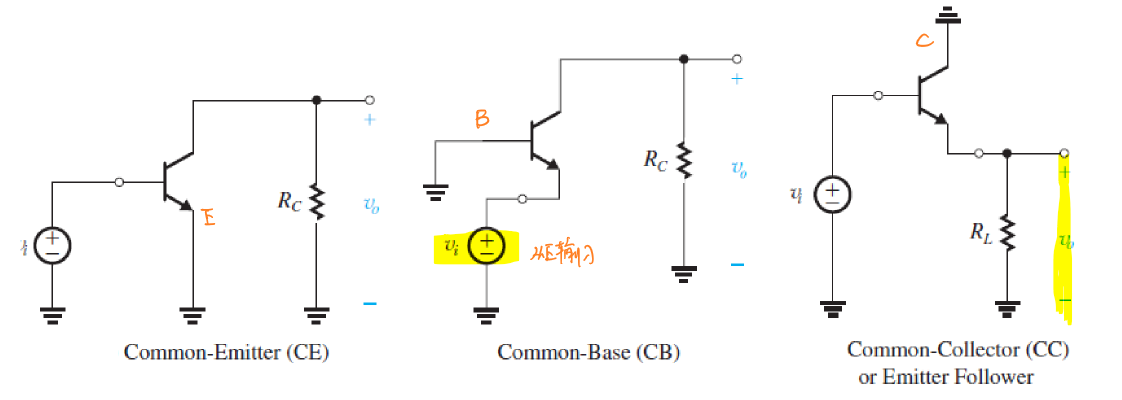
总体上来说，晶体管的哪个集被共用，电路中晶体管的哪个极就接地。
三种放大电路的特性不尽相同，用途也不相同，本节主要介绍这三种放大电路的电路分析和特性。

共射极（CE）放大电路

共射极放大电路如下图所示：

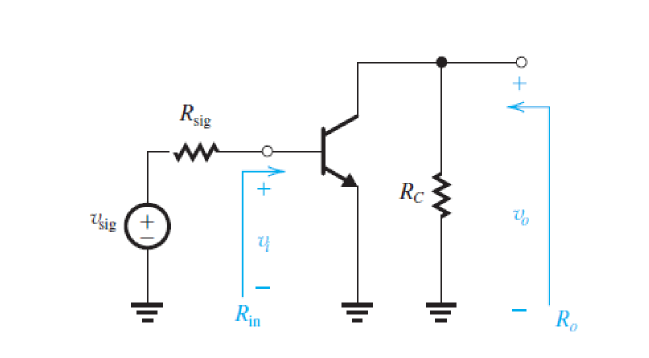
电压信号由基极输入、集电极输出。

π模型的电路分析

当发射极没有额外的电阻时，因此使用π模型进行等效处理：

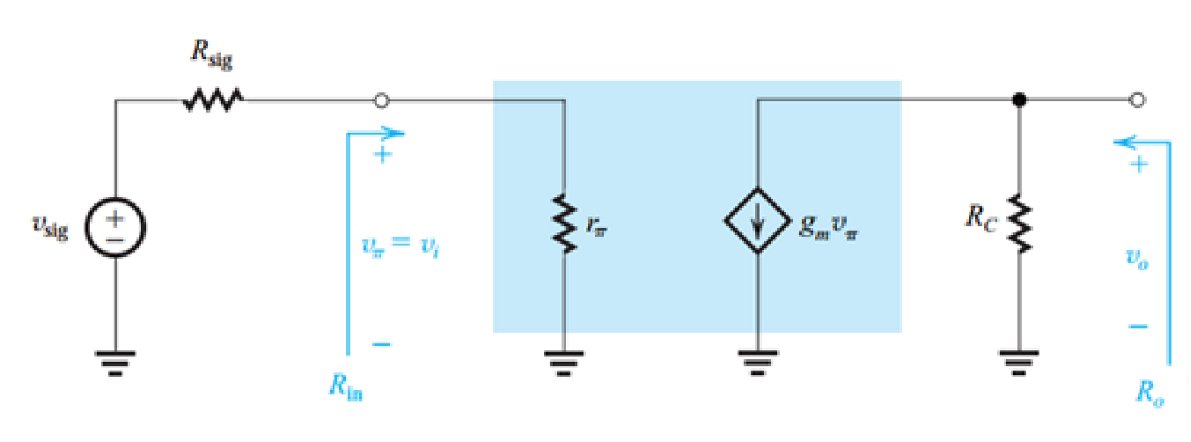
在该电路中，放大电路部分（图中蓝色框）的输入电阻：
\[R_{in}=\frac{v_i}{i_b}=r_π\] 而\(r_π=\frac{β}{g_m}\)，\(g_m=\frac{I_C}{V_T}\)，通常来说放大电路内部的输入电阻较小，但是数量级仍然在几千欧姆。
当\(v_{in}=0\)（端口输入电压）时，从输出端看电路电阻，可以得到放大电路部分的输出电阻：
\[R_o=R_C\] 可见放大电路部分的输出电阻由\(R_C\)的阻值决定，通常\(R_C\)的阻值都比较大，数量级在几千欧姆左右。
放大器的电压增益就可以表示为：
\[A_v=\frac{v_o}{v_{sig}}\] \[v_o=-g_mv_π×R_C\] \[v_π=v_{sig}\frac{r_π}{r_π+R_{sig}}\] \[A_v=-g_m\frac{r_π}{r_π+R_{sig}}R_C\] 由于放大电路的开环增益与电压增益的关系为:\(A_v=A_{vo}\frac{R_{in}}{R_{in}+R_{sig}}\)，因此电路的开环增益表示为：
\[A_{vo}=-g_mR_C\]

T模型电路分析

当发射极存在额外的电阻\(R_e\)时，采用T模型对电路进行分析：

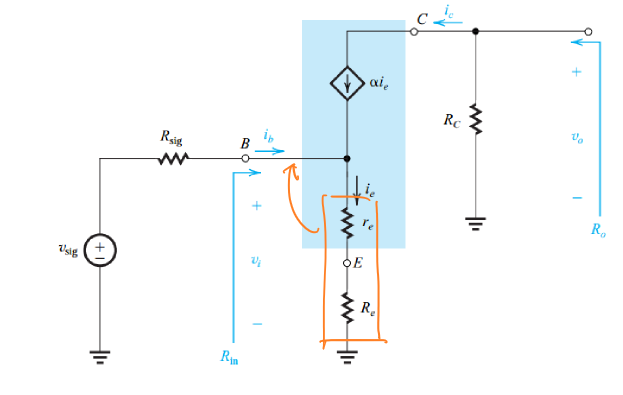
由于发射极接地，不便于电阻分析，因此采用电阻投射定理将发射极的电阻转到基极上进行计算。
那么输入电阻：
\[R_{in}=(r_e+R_e)(β+1)=r_π\] 输出电阻：
\[R_o=R_C\] 那么电压增益可以表示为：
\[A_v=\frac{v_o}{v_{sig}}\] 应用电阻投射定理将\(R_{sig}\)转到发射极以求出\(i_e\)：
\[i_e=\frac{v_{sig}}{(r_e+R_e)+\frac{R_{sig}}{β+1}}\] \[v_o=-i_cR_C=-αi_eR_C=-\frac{αv_{sig}R_C}{(r_e+R_e)+\frac{R_{sig}}{β+1}}\] \[A_v=-\frac{αR_C}{(r_e+R_e)+\frac{R_{sig}}{β+1}}\] 由\(α=\frac{β}{\beta+1}\):
\[A_v=-β\frac{R_C}{(r_e+R_e)(β+1)+R_{sig}}\] 由\(r_π=(r_e+R_e)(β+1)=\frac{β}{g_m}\):
\[A_v=-g_m\frac{r_π}{r_π+R_{sig}}R_C\] 电路的开环增益同样为：
\[A_{vo}=-g_mR_C\]

共射极放大电路的特性

由开环增益的表达式可以发现，输入电阻\(R_{in}=r_π\)增大，\(g_m\)下降，\(|A_{vo}|\)减小。根据反馈电路中对开环增益与稳定性的分析：开环增益越小，系统越稳定。
因此，输入电阻应该尽量地大，而输出电阻\(R_C\)也应当尽量地小才能保证系统的稳定性。
在实际中，可以在输入端之前加入一个缓冲器/跟随器，以提高输入电阻的阻值。

共基极(CB)放大电路

共基极放大电路如下图所示：

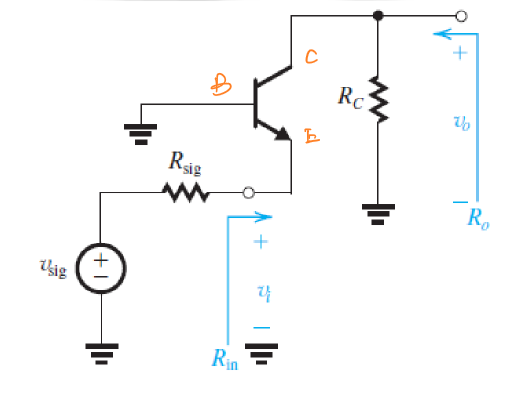
电压信号\(v_{sig}\)在发射极作为输入信号，集电极处\(R_C\)上的电压作为输出电压。

T模型电路分析

由于发射极存在电阻，因此采用T模型进行分析：

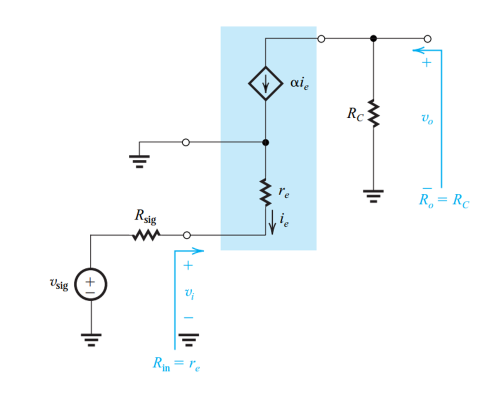
T模型中放大电路的输入电阻：
\[R_{in}=-\frac{v_i}{i_e}=r_e\] 由于\(r_e=\frac{α}{g_m}\)，因此放大电路内部的输入电阻比较小，在几十欧姆左右。

假设输入电压为0，从输出端看电阻，则输出电阻为：
\[R_o=R_C\] 可见放大电路部分的输出电阻由\(R_C\)的阻值决定，通常\(R_C\)的阻值都比较大，数量级在几千欧姆左右。
则放大电路的电压增益表示为：
\[A_v=\frac{v_o}{v_{sig}}\] \[\begin{aligned} v_o&=i_cR_C \\ &=-αi_eR_C \\ &=-α(-\frac{v_{sig}}{v_{sig}+r_e})R_C\\ \end{aligned}\] \[A_v=\frac{v_o}{v_{sig}}=α\frac{R_C}{R_{sig}+r_e}\] 其开环增益：
\[A_{vo}=α\] 由于\(α≈1\)，因此共基极放大器的电压增益与晶体管电流增益\(β\)无关。同时\(R_{sig}\)、\(R_C\)的阻值常处于同一数量级，因此共基极放大电路的电压增益很小。

共基极放大电路的特性

由于输入阻抗/阻值过于低，与理想放大器要求的“输入阻抗无穷大”矛盾，因此绝大多数情况下不适合作为放大电路工作。
但是，由于其开环增益相对独立，因此共基极放大电路不容易受到频率的影响，在高频部分表现较为稳定。
此外，其输入阻值的数量级正好和同轴线缆的阻值差不多，因此可以在使用同轴线缆的高频电路中使用，实现和线缆的阻抗匹配，以减小信号的能量反射损失。

共集极(CC)放大电路/发射极跟随器

共集极放大电路的结构如下图所示：

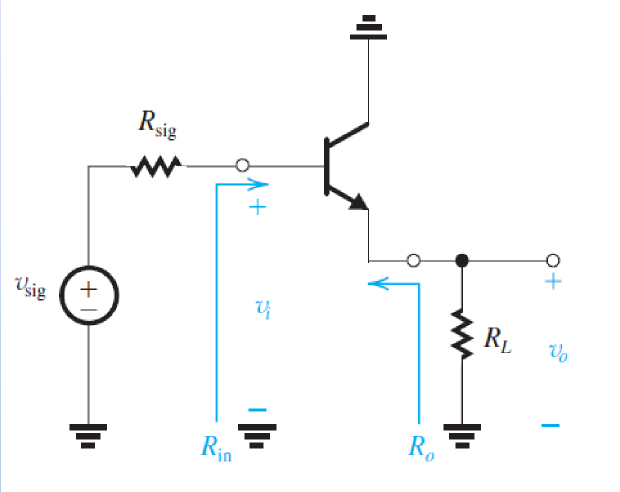
共集极以基极作为输入信号源，同时在发射极连接一个负载电阻\(R_L\)作为电路的输出。

T模型电路分析

由于发射极存在电阻，因此采用T模型进行分析：

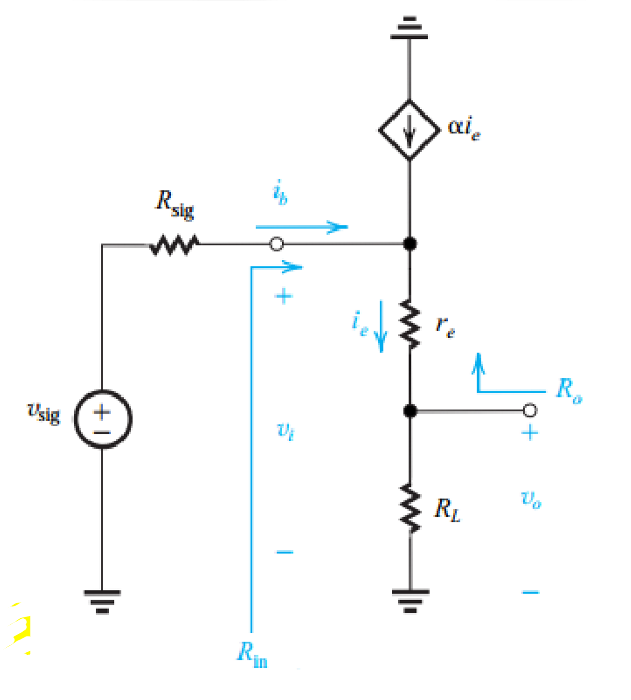
输入电阻：
\[i_b=\frac{v_i}{(β+1)(r_e+R_L)}\] \[R_{in}=(r_e+R_L)(1+β)\]

输出电阻：
如果端口输入电压\(v_{in}=0\)，那么从放大电路的输出端看电阻：
\[R_o=r_e\]

电路的电压增益为：
\[v_{in}=\frac{R_{in}}{R_{in}+R_{sig}}v_{sig}\] \[v_o=v_{in}\frac{R_L}{R_L+r_e}\] 其中\(v_{in}\)和\(v_{o}\)表示放大电路部分（对应晶体管）的输入电压和输出电压。
\[A_v=\frac{v_o}{v_{sig}}=\frac{R_L}{R_L+r_e}\frac{R_{in}}{R_{in}+R_{sig}}\] 带入\(R_{in}\),得到：
\[\begin{aligned} A_v&=\frac{R_L}{R_L+r_e}\frac{(r_e+R_L)(1+β)}{(r_e+R_L)(1+β)+R_{sig}}\\ &=\frac{(β+1)R_L}{(β+1)(r_e+R_L)+R_{sig}} \end{aligned}\]

电路的开环增益由\(R_L→∞\)给出：
\[A_{vo}=\lim_{R_L→∞}\frac{v_o}{v_{in}}=\lim_{R_L→∞}\frac{R_L}{R_L+r_e}=1\] \[A_{vo}=1\] 因此，电路的开环增益等于1。

共集极放大电路的特性

共集极放大电路的开环增益恒等于1，因此在电路中常常作为缓冲器/跟随器使用。

完整的晶体管放大电路

上述的电路分析都是基于小信号模型，在小信号模型中只考虑的交流信号所带来的影响。现在回到大信号模型，同时考虑输入信号的直流分量。此时电路需要在晶体管的三极各设置一个耦合电容以隔绝直流的影响，其余部分保持不变。电路的特性和增益等交流分析的结论仍然适用。

完整的放大电路结构

• 共发射极放大电路
  

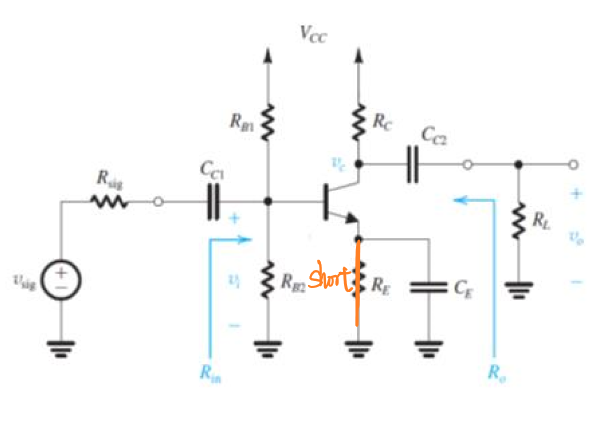
图中发射极处的电容称为旁路电容（By-pass Capacitor）其作用是在高频交流信号输入时将与其并联的电阻短路。

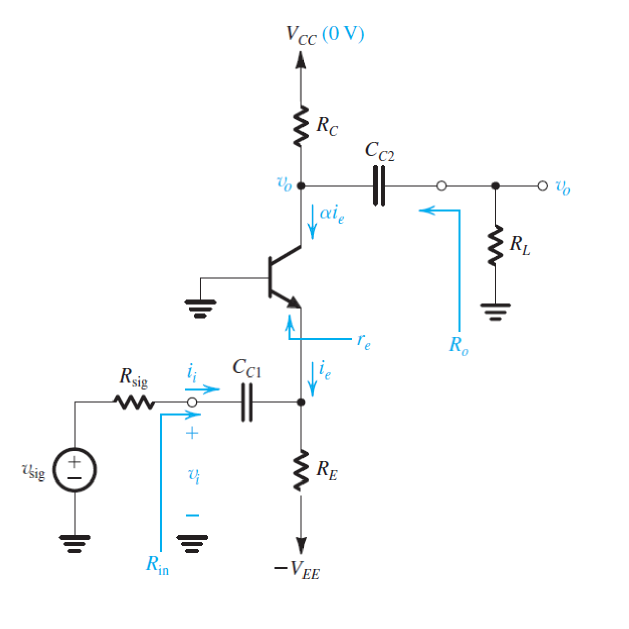
• 共基极放大电路
  

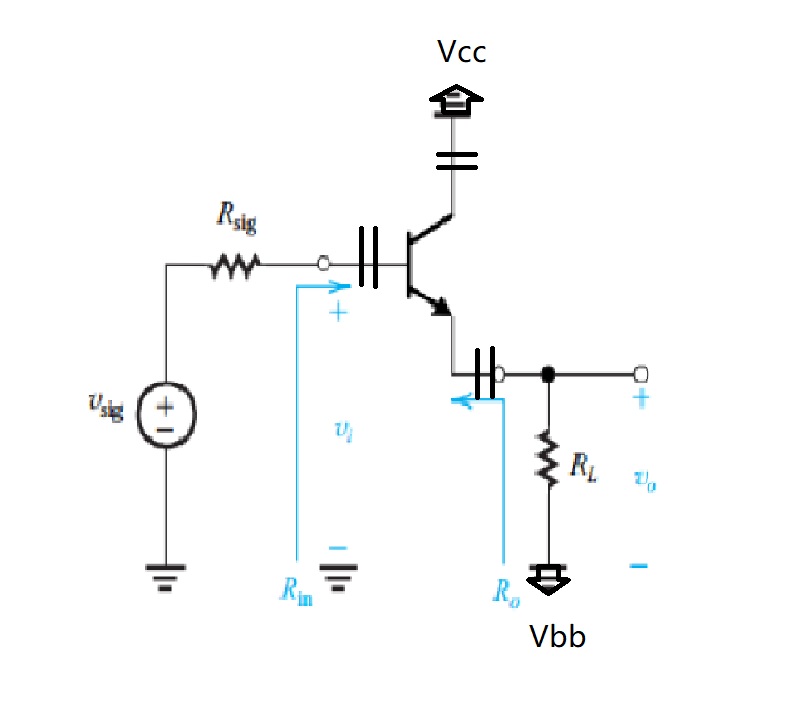
• 共集极放大电路
  

放大电路的频率响应

由于完整的放大电路中存在电容，当输入的电压信号频率较低时，这些电容的容抗无法在电路分析中忽略，因此放大电路的增益在输入信号为低频信号时有所损失。
下图表示了晶体管放大电路的频率响应特性曲线：

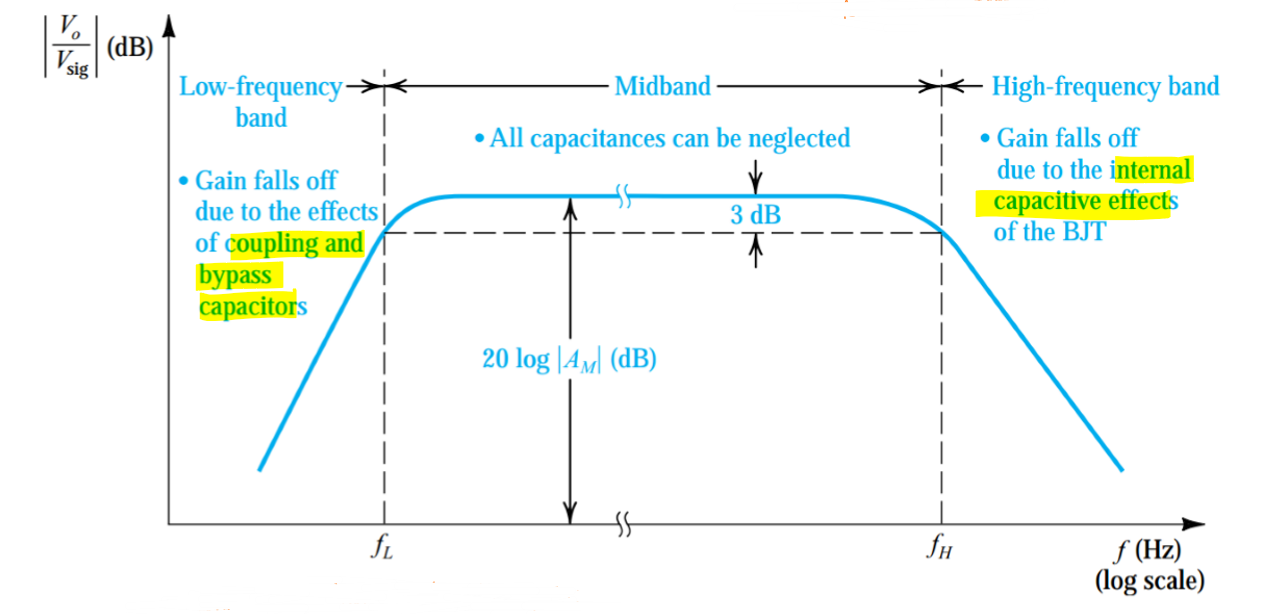
集成放大器中（比如第10讲的多级放大电路）不存在电容，因此其性能不会受到输入信号中低频分量的影响。但是高频时晶体管内部的类似电容的表现特性也会使得其性能在高频时存在损失。

在低频输入下，电路中电容不再视为短路。整个电路的低频截止频率\(f_L\)可以是电路中的每一个电容的截止频率的线性叠加：
\[f_L=\frac{1}{2π}∑_i\frac{1}{C_iR_{Ci}}\] 其中\(R_{Ci}\)为单看其中一个电容，其他电容视为短路时，电容电阻构成的滤波器电路中的等效电阻。
> 求电路的低频截止频率：
> 1. 单看其中一个电容，剩下电容视为短路。
> 2. 画出等效的滤波器电路模型，找到等效电阻。
> 3. 所有的电容对应的等效电阻都被找到，求每个电容的截止频率，再线性叠加。

放大电路类型	\(R_{in}\)	\(R_{o}\)	\(A_v\)	\(A_{vo}\)	特性
CE	\(r_π\) 越大越好	\(R_C\) 越小越好	\(-g_m\frac{r_π}{r_π+R_{sig}}R_C\)	\(-g_mR_C\)	内部的输入和输出阻值都在几千欧姆 相比之下输入阻值较小。
CB	\(r_e\)	\(R_C\)	\(α\frac{R_C}{R_{sig}+r_e}\)	\(α\)	输入阻值过小 电压增益很小 开环增益独立
CC	\((r_e+R_L)(1+β)\)	\(r_e\)	\(\frac{(β+1)R_L}{(β+1)(r_e+R_L)+R_{sig}}\)	\(1\)	开环增益恒等于1