滤波器

传输函数

输出值与输入值的比值，以电压的形式来表示： \[T(s)=\frac{V_{out}}{V_{in}}\]

电容的值是随着频率的变化而变化的：

\(τ=RC\), \(ω=\frac{1}{τ}\)

低通滤波器

传输函数：
\[T(Jω)=\frac{V_{out}}{V_{in}} =\frac{\frac{1}{S}C}{R+\frac{1}{S} C}\] 根据电容的位置，可以判断是高通还是低通。
低通滤波器的电容接在了输出端，如果电流的频率很底，输出端为开路，输出端电压=输入端电压，传输函数为1。
当频率增加到一定程度时，传输函数的值（\(|T|dB\)）比频率为0时的值低3dB（即下降0.707）时，可以认为传输函数的值开始下降。此时的频率为\(\frac{1}{RC}\)（称为低频截止频率）。
如果电流频率高，电容相当于短路，输出端短路，输出电压为0，所以能够阻断电压。

高通滤波器

传输函数：
\[T(Jω)=\frac{V_{out}}{V_{in}} =\frac{s τ}{1+s τ}\] 电容的位置接在输入端和输出端之间，如果电流的频率很低，输出端为短路。如果电流的频率很高，电容相当于断路。
低通滤波器和高通滤波器的截止频率是相同的。

带通滤波器

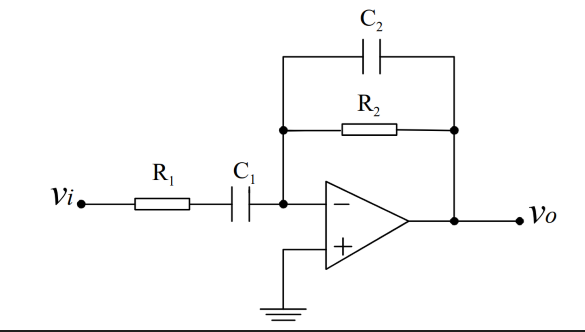
传输函数：
\[T(Jω)=\frac{V_{out}}{V_{in}} =−\frac{Kj 2πf}{1+\frac{j ω}{ω_1 }1+\frac{j ω}{ω_2 }}\] 如果要实现滤波器，必须要有一个电容或者电感。
\(C_1\)电流频率很低，\(C_1\)为开路，输入电压和放大器的反向输入端\(（-）\)被断开，放大器的输入信号为0.
\(C_2\)电流频率很高，\(C_2\)为短路，\(R_2\)为短路，运算放大器的输出端和反向输入端被短路，输出电压接地，输出电压为0.
输入电压的频率只能在\(f_1=\frac{1}{2 πR_1 C_1 }\)与\(f_2=\frac{1}{2 πR_2 C_2 }\)之间，才能够通过滤波器。