通信原理-知识点总结

信息和通信系统参数

信息

信息量： \[I=log_a\frac{1}{P(x)}=-log_aP(x)\] 信息熵： \[H=∑_{i=1}^MP(x_i)\log_2\frac{1}{P(x_i)}=∑_{i=1}^MP(x_i)I_i\]

通信系统的重要参数

有效性指标

传输速率：
\[R_b=R_Blog_2M\] \(R_b\)是比特率，\(R_B\)是符号速率。

记忆方法：通常一个符号对应多个字节，因此符号速率是小于比特率的。

频谱效率:
\[η=\frac{R_B}{B}\]

可靠性指标

误码率：
即原本信息为“1”判决后为“0”的概率和原本信息为“0”判决后为“1”的概率之和。
\[P_e=P(0|1)+P(1|0)\]

信噪比：
信噪比表示为信号的功率与噪声的功率之比：
\[SNR=\frac{P_S}{P_N}\]

香农容量：
在误码率为0的情况下，信息系统的理论最大速率\(R_b\)称为香农容量，即带宽利用率与系统带宽相乘。
\[C=Blog_2(1+SNR)=η_bB\]

通信系统的两次编码

信源编码（Source Encoding）：提升有效性
信道编码（Channel Encoding）： 提升可靠性

信号的数学和统计特性

信号的数学特性

如果信号可以表示为\(S(t)\):
直流信号是信号在一周期内的平均值：
\[S_{dc}=\lim_{T→∞}\int_{-\frac{T}{2}}^{\frac{T}{2}}S(t)dt\]

定义时间均值函数： \[\overline{f(t)}=\lim_{T→∞}\frac{1}{T}∫_{-\frac{T}{2}}^\frac{T}{2}f(t)dt\] 当\(f(t)\)是一个周期函数时，其时间均值为0。

其功率信号是其平方的时间均值：
\[P=\lim_{T→∞}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}|S(t)|^2dt\] 功率信号也可以表示为其功率谱密度函数\(P_f(t)\)的积分:
\[P=\frac{1}{2π}∫_{-π}^πP_f(ω)dω\]

其功率谱函数可以由维纳——辛钦定理得到：
功率信号的自相关函数和功率谱密度函数为傅里叶变换对。
\[P_f(t)=∫R_S(t)e^{-jωt}dt\]

随机过程的统计特征

• 期望 \[E_ξ(t)=∫ξ(t)f_1(x,t)dt\] 其中\(ξ(t)\)是含有随机变量\(x\)的随机过程，\(f_1(x,t)\)是\(x\)的概率密度函数。
• 方差 \[D_ξ(t)=E(ξ^2(t))-[E_ξ(t)]^2\] 随机过程的方差表示随机过程值围绕期望的摆动幅度。
  
• 自相关函数 \[R(t,t+τ)=E[ξ(t)ξ(t+τ)]=∫f_1(t)ξ(t)ξ(t+τ)dt\]

两种特殊的随机过程

• 平稳随机过程
  1. 期望是一个常数。
  2. 自相关函数只与τ有关。
     
• 遍历性随机过程
  遍历随机过程最大的特点是过程中的任意一个随机变量\(x(t)\)的在时间上的统计特性和这个随机过程\(ξ(t)\)的统计特性相等。
  1. 计算过程中任意一个随机变量的期望：\(E(x)=∫xf(t)dt\)
     
  2. 计算随机过程的时间均值：\(\lim_{T→∞}\frac{1}{T}∫_{-T/2}^{T/2}f(t)dt\)
     
  3. 证明两者相等

功率信号的统计性质

在通信系统中，功率信号是一个宽平稳随机过程，下面使用自相关函数研究其性质。
> 此处自变量为τ（如平均功率为τ=0）

功率信号	自相关函数	注解
平均功率	\(R(0)=E(ξ^2(t))\)
直流功率	\(R(∞)=E^2(ξ(t))\)	当τ→∞时，表示为两个不相关信号的自相关函数
交流功率	\(R(0)-R(∞)=σ^2\)	平均功率=交流功率+直流功率

求解平均功率的方式：
1. \(R(0)\) 2. \(E(ξ^2(t))\) 3. 谱密度函数的积分 - 对于角频率谱密度函数：\(\frac{1}{2π}∫P_ξ(ω)dω\) - 对于频率密度函数：\(∫P_ξ(f)df\)

随机过程通过线性系统

如果线性系统的输入信号是一个平稳随机过程，那么输出信号也必然是一个平稳随机过程。
假定线性系统的频域方程为\(H(ω)\)，有如下结论：

	输入过程	输出过程
分布类型	平稳随机过程	平稳随机过程
均值	\(a\)	\(aH(0)\)
功率谱密度	\(P(ω)\)	\(\lvert H(ω) \rvert ^2P(ω)\)

高斯白噪声

高斯白噪声指信号的功率谱密度函数在频域内符合均匀分布、概率密度函数符合高斯分布的噪声。高斯白噪声是一种可加性噪声。

高斯白噪声的统计特性

均值：\(E_ξ(ω)=0\)
方差：\(D_ξ(ω)=0\)
自相关函数：\(R_n(τ)=\frac{n_0}{2}δ(τ)\)

高斯白噪声通过滤波器

通过低通滤波器：
平均功率：即频谱的面积，\(n_0B\)
自相关函数：\(\frac{n_0}{2}G_{2B}(ω)↔R(τ)=\frac{n_0τ}{2}Sa(\frac{Bτ}{2}),B=ω_c\)

通过带通滤波器：
平均功率：即频谱的面积，\(n_0B\)
自相关函数：\(R_n(τ)=\frac{n_0B}{4π}Sa(\frac{Bτ}{2})cos(ω_0τ)\)。

波形成分及其统计特性

窄带高斯白噪声的谱密度函数可以以包络相位形式和同相正交形式表现：
- 包络相位 \[n_0(t)=a(t)cos[ω_ct+φ(t)]\] 其中\(a(t)\)为随机包络函数，服从瑞利分布(Rayleigh Distribution)；\(φ(t)\)为随机相位函数，服从均匀分布(Uniform Distribution)。 - 同相正交 \[n_0(t)=n_ccosω_ct-n_s(t)sinω_ct\] 同相分量和正交分量的统计特性： 一个均值为0的窄带平稳高斯过程，其同相分量和正交分量也是平稳高斯过程，且均值为0，方差和原信号相同。

高斯白噪声通过低通滤波器

设低通滤波器的带宽为\(B\):
此时的平均功率可以由谱密度函数的面积表示：
\[\overline{N(t)}=\frac{n_0}{2}×2B=n_0B\] 其自相关函数可以通过傅里叶变换来获得：
\[R_n(τ)=\frac{n_0B}{2π}Sa(Bτ)\]

模拟传输系统

调制的目的

使用调制的目的有三个：
1. 由于天线与传输信号的波长之间存在匹配关系，通常天线的尺寸在\(\frac{λ}{10}\)到\(\frac{λ}{4}\)之间，经过调制的信号波长会变小，因此对应的传输天线的尺寸会对应减小以便于传输。
2. 调制使得多频复用称为可能，多个基带信号可以与不同的载波结合，实现同时传输多个基带信号。
3. 扩展信号带宽，提高系统抗干扰能力。

线性调制方法

线性调制后，不会有新的频率成分产生。因此线性调制只能在受调参量为幅度时使用。
线性调制的方法分为：调幅（AM），双边带调制（DSB），单边带调制（SSB），残留边带调制（VSB）。这几种线性调制方法简图如下图所示：

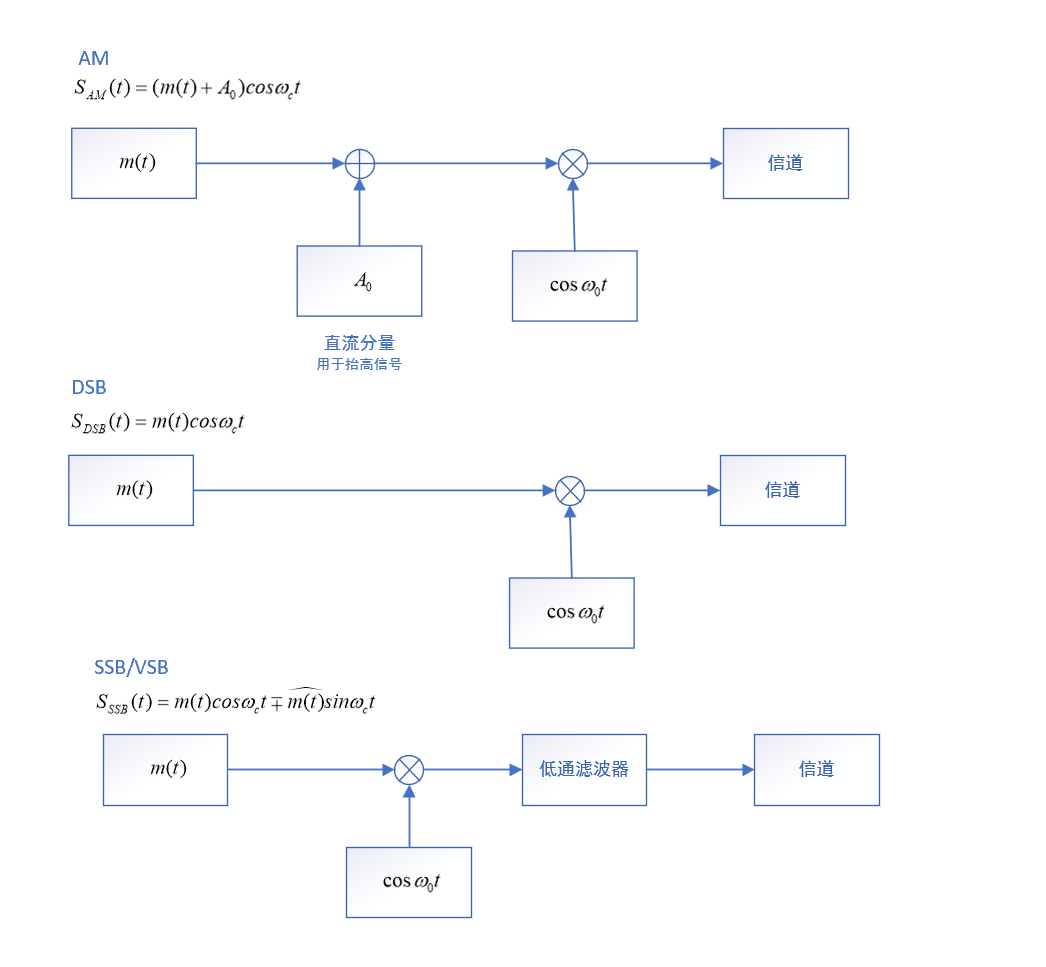
• AM： 输入信号加上直流分量后与载波相乘。
  
• DSB： 输入信号直接与载波相乘。
  
• SSB/VSB： 输入信号与载波相乘后通过低通滤波器。

线性调制的参数：

线性调制方法	输出表达式	带宽	调制后功率\(P_{TX}\)	调制端噪声	无衰减下的输入信噪比\(SNR_i\)
调幅(AM)	\(S_{AM}=(A_0+m(t))cosω_ct\)	\(2f_H\)	\(\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}\)	\(2n_0f_H\)	\(\frac{A_o^2+\overline{m^2(t)}}{4n_0f_H}\)
双边带调制(DSB)	\(S_{DSB}=m(t)cosω_ct\)	\(2f_H\)	\(\frac{\overline{m^2(t)}}{2}\)	\(2n_0f_H\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)
单边带调制(SSB) 残留边带调制(VSB)	\(S_{SSB}=\frac{1}{2} m(t)cosω_ct∓\frac{1}{2}\hat{m(t)}sinω_ct\) \(\hat{m(t)}\) 表示\(m(t)\) 相移 \(-\frac{π}{2}\) 的结果 即希尔伯特变换 保留上边带为“-”，下边带为“+”	\(f_H\)	\(\frac{\overline{m^2(t)}}{4}\)	\(n_0f_H\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)

线性调制的解调方法分为两类：相干解调和非相干解调，两者的简图如下图所示：

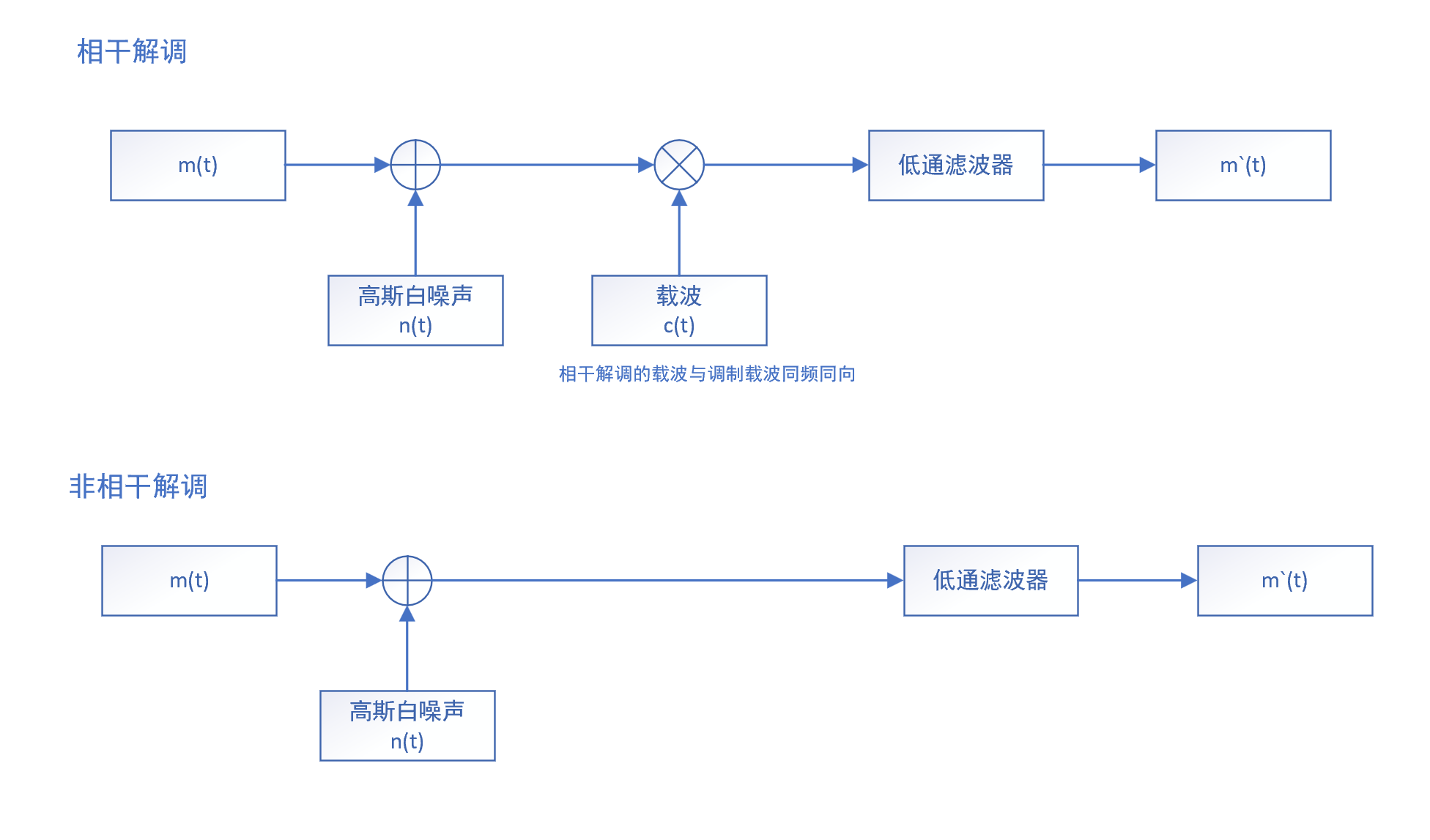
• 相干解调： 在解调端调制信号与一个同频同相的载波相乘。
  
• 非相干解调： 通过低通滤波器消除高频分量后直接得到包络线波形。

线性解调的参数：
- 相干解调之后，噪声功率只有原来的\(\frac{1}{4}\)。
- 非相干解调之后，噪声功率与原来相同。

信噪比增益：
\[G=\frac{SNR_o}{SNR_i}\] 即解调端的信噪比与调制端的信噪比之比。

线性调制方法	输出信号	解调后功率	解调后噪声	输出信噪比\(SNR_o\)	信噪比增益
调幅	\(\frac{1}{2}m(t)\)	\(\frac{1}{4}\overline{m^2(t)}_{co}\) \(\overline{m^2(t)}_{noc}\)	\(\frac{n_0f_H}{2}_{co}\) \({2n_0f_H}_{noc}\)	\(\frac{\overline{m^2(t)}}{2n_0f_H}_{co}\) \(\frac{\overline{m^2(t)}}{2n_0f_H}_{noc}\)	\(\frac{2\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}≤\frac{2}{3}\)
双边带调制	\(\frac{1}{2}m(t)\)	\(\frac{1}{4}\overline{m^2(t)}\)	\(\frac{n_0f_H}{2}\)	\(\frac{\overline{m^2(t)}}{2n_0f_H}\)	\(2\)
单边带调制	\(\frac{1}{4}m(t)\)	\(\frac{1}{16}\overline{m^2(t)}\)	\(\frac{n_0f_H}{4}\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)	\(1\)

调幅指数

由于对标准调幅的解调实质上是求得其包络线函数，在波形图上观察，当\(m(t)<A_0\)时，波形图的上下包络线会发生重叠从而无法还原之前的包络线函数，导致失真。
因此要求:
\[|m(t)|_{max}≤A_0\] 定义调幅指数\(β_{AM}\)反映\(|m(t)|_{max}\)与\(A_0\)的关系：
\[β_{AM}=\frac{|m(t)|_{max}}{A_0}\] - \(β_{AM}<1\)： 正常调幅 - \(β_{AM}=1\)： 满调幅 - \(β_{AM}>1\)： 过调幅

调制效率

由于载波不携带任何信息，定义调制效率为边带功率（\(P_s=\frac{\overline{m^2(t)}}{2}\)）与总功率（\(P_s+P_c=\frac{\overline{m^2(t)}}{2}+\frac{A^2_0}{2}\)）之比以反映调制时信息的占比：
\[η=\frac{P_s}{P_s+P_c}\]

信道衰减·输入信噪比

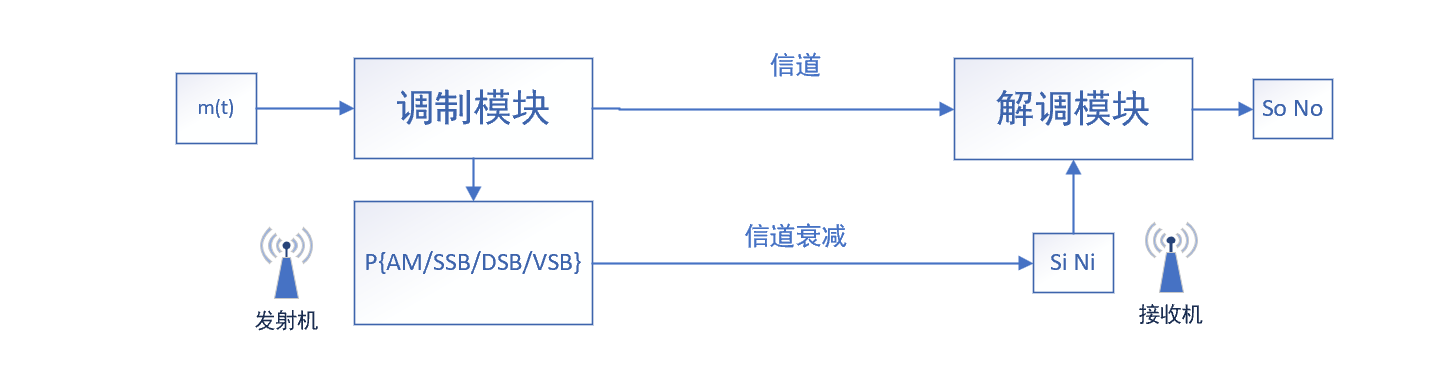
经过线性调制后的信号通过发射机(TX)发送，进入信道，在信道中由于干扰和噪声，导致信号功率出现损失，使得接收机(RX)接收的信号功率与发射机发射的信号功率不同，定义信道中的衰减（ATU）为发射机发射功率与接收机接收功率之比：
\[ATU|dB=10lg\frac{P_{TX}}{P_{RX}}\] 因此，在解调模块处，接收机接收到的功率可以表示为：
\[P_{TX}=P_{RX} × ATU=P_{AM/DSB/SSB}\] 在这个过程中，假设噪声通过信道时不会发生任何改变，噪声的功率仍然与基带信号中的噪声功率相同。

定义输入信噪比(\(SNR_i\))为输入进解调模块的信噪比：
\[SNR_i=\frac{S_i}{N_i}\] 其中，\(S_i=P_{RX}=P_{AM/DSB/SSB} / ATU\)。
\(N_i=N_{modulation}=n_0B\)。

非线性调制方法*

调相

调相后的波形：
\[\begin{aligned} S_{PM}(t)=&Acos(ω_ct+K_pm(t))\\ =&Acos(ω_ct+K_pA_mcosω_mt) \end{aligned}\] 其中\(K_p=ϕ(t)/m(t)\)为相位敏感度，\(m_p=K_pA_m\)称为调相指数。 最大相偏：\(K_pA_m\)

调频*

调频后的波形：
\[\begin{aligned} S_{FM}(t)=&Acos(ω_ct+K_f∫m(t)dt)\\ &=Acos(ω_ct+\frac{K_fA_m}{ω_m}sinω_mt) \end{aligned}\] 其中\(K_fm(t)=\frac{d}{dt}ϕ(t)\)，\(K_f\)为频率敏感度；\(m_f=\frac{K_fA_m}{ω_m}\)称为调频指数。

宽带下的调频特性：
- 带宽：\(2(m_f+1)f_H\)
- 调制后功率：\(\frac{A^2}{2}\) - 信噪比增益：\(3m^2_f(m_f+1)\) - 最大频偏：\(K_fA_m\)

调幅和调频的关系

\(m(t)\)积分后的信号通过积分器后调相的结果是其调频结果。
\(m(t)\)微分后的信号通过微分器后调频的结果是其调相结果。

所有调制方法的性能对比

可靠性
解调端输入信号能量\(S_i\)相同的前提下，信噪比越大，可靠性越高。
\[AM＜DSB=SSB＜FM\] 有效性
带宽越大，有效性越低。
\[FM＜AM=DSB＜VSB＜SSB\]

数字基带传输系统

模拟信号采样

对基带信号，最佳的采样频率为：
\[f_s=2f_H\]

对带通信号，最佳的采样频率为：
\[f_s=2B(1+\frac{M}{N})\] 其中\(M\)为\(|\frac{f_H}{B}|\)的小数部分，\(N\)为\(|\frac{f_H}{B}|\)的整数部分。

模拟信号的数字化方法：脉冲编码调制

脉冲编码调制的格式为：

	极性码	段落码	段内码
	\(C_1\)	\(C_2C_3C_4\)	\(C_5C_6C_7C_8\)
意义	极性	对应8个段落	对应每一个段落中的16个量化级

PCM编码与数字化的13折A压缩律对应如下：

段落编号	电平区间	段落码	量化间隔Δ
1	0-16	000	\(1=2^0\)
2	16-32	001	\(1=2^0\)
3	32-64	010	\(2=2^1\)
4	64-128	011	\(4=2^2\)
5	128-256	100	\(8=2^3\)
6	256-512	101	\(16=2^4\)
7	512-1024	110	\(32=2^5\)
8	1024-2048	111	\(64=2^6\)

脉冲调制编码过程

量化后的电平值转化为脉冲调制编码的步骤为：
1. 判断电平的正负，如果是正：\(C_1=1\)，如果为负，\(C_1=0\)。 > 注意“1正0负”

2. 根据电平值和电平区间，判断电平落在了哪一个段落，决定段落码\(C_2C_3C_4\)。
   
3. 将电平值减去段落的起始值，与量化间隔相除，结果转化为8421码即为\(C_5C_6C_7C_8\)。

与量化间隔相除结果的余数部分无法通过编码表示，称为编码噪声\(N_e\)。

脉冲调制解码过程

PCM编码在解码端首先会变成11位的自然二进制编码。
PCM编码转换为10进制后的结果与11位的自然二进制转换为10进制的结果相同。
\[I_{11-NBC}=I_{PCM}\] 因此PCM编码只需要转换为10进制，在开头补充0即可转换为11位NBC码。
由于PCM编码只考虑到了每个量化区间内的起始值\(m_{i-1}\)而并非量化电平\(p_i\)，在解码过程中需要补充每个量化段的半个量化区间\(\frac{Δ_i}{2}\)，由于最小的\(\frac{Δ_1}{2}=0.5\)，因此需要额外补充一个bit来弥补增加的精度，生成12位NBC码。
12位NBC的精度高于8位PCM编码，与PCM编码相比，12位NBC能额外表达一个当前量化段的一半的量化间隔，进而减少了量化噪声。
12位NBC可以通过在PCM转化为11位NBC码后，11位NBC码的最后一个“1”后增加一个“1”即可。
\[I_{12-NBC}=I_{PCM}+\frac{1}{2}Δ_i\] 因此，整个脉冲编码调制的量化噪声\(N_q\)为编码噪声减去\(\frac{Δ_i}{2}\): \[N_q=N_e-\frac{Δ_i}{2}\]

脉冲编码调制的性能

• 传输速率
  PCM的传输速率为：
  \[R_b=f_s×log_2M×n\] 其中\(f_s\)为采样速率，\(M\)为比特数，A律13折PCM中\(M=256\)。\(n\)为信号的路数。
  
• 信噪比
  整个过程的信噪比表示为：
  \[\frac{S_o}{N_o}_{PCM}=\frac{\overline{m^2(t)}}{N_q+N_e}\] 通过计算可以发现，当\(m(t)\)服从均匀分布时，量化信噪比表示为：
  \[\frac{S}{N_q}=M^2\]

码型选择

对每一帧而言，其中电平不为0的时间段（即信息传输的时间）称为符号持续时间\(τ\)（Symbol duration），定义占空比（Duty Cycle）表示符号持续时间和一个周期时间之比：
\[Duty.Cycle=\frac{τ}{T_s}×100\%\] 当\(τ=T_s\)时，表示一个周期内所有时间都在发送符号，称为归零码（RZ Code），\(τ≠T_s\)时，称为不归零码（NRZ Code）。

码型	有无直流分量	是否可以提取同步脉冲
单极性不归零码	有	否
单极性归零码	有	是
双极性不归零码	无	否
双极性归零码	无	是 注：需要通过整流器

双极性归零码虽然不能直接提取定时脉冲，但可以通过使用一个整流器转换为单极性归零码，从而提取出定时脉冲，且无直流分量。

HDB₃ 码

HDB₃的编码规则基本和AMI码相同，但相比于AMI码，其规定在连续三个0信号出现时加入一个破坏脉冲V以防止过长0信号导致定时脉冲难以提取的问题。HDB₃码的编码规则如下：
1. 给定一个初始符号以指定消息编码中起始1的极性，使用AMI编码方式对消息进行编码。起始1的极性与初始符号的极性相反。
2. 当有连续4个0信号出现时，第四个0信号改为破坏脉冲V，对破坏脉冲的极性有如下规定：
i）V的极性交替反转（高优先级）
ii）破坏脉冲的极性与前一个“1”或“V”的极性相同
3. 在V的极性不满足条件2时，连0信号的第一个0变为补性码B'，B'的极性与其后一个V的极性相同。B'后的1全部反转极性。
4. V和B'保留极性，并替换为“1”。

曼彻斯特码

曼彻斯特码/双向码

曼彻斯特码是一种双极性不归零码，其01编码为脉冲信号的上升沿和下降沿，巧妙地解决了长连0信号由于电平不发生变化而导致的定时脉冲提取困难的问题。其编码规则为：
脉冲波形在同步脉冲间隔周期50%时：
- 脉冲上升沿表示逻辑1
- 脉冲下降沿表示逻辑0

例如：

差分曼彻斯特码

差分曼彻斯特码的编码规则为：
脉冲间隔开始时：
- 脉冲电平不发生变化（无触发沿）表示逻辑1 - 脉冲电平发生变化（有触发沿）表示逻辑0

例如：

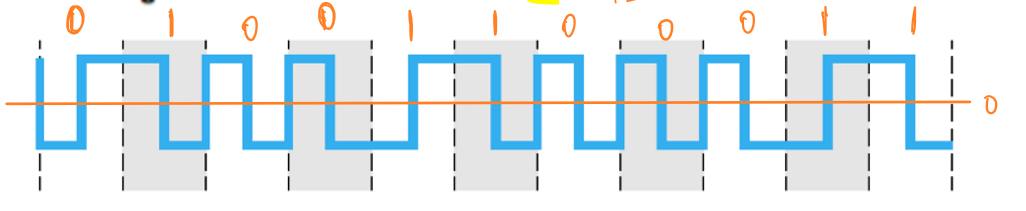
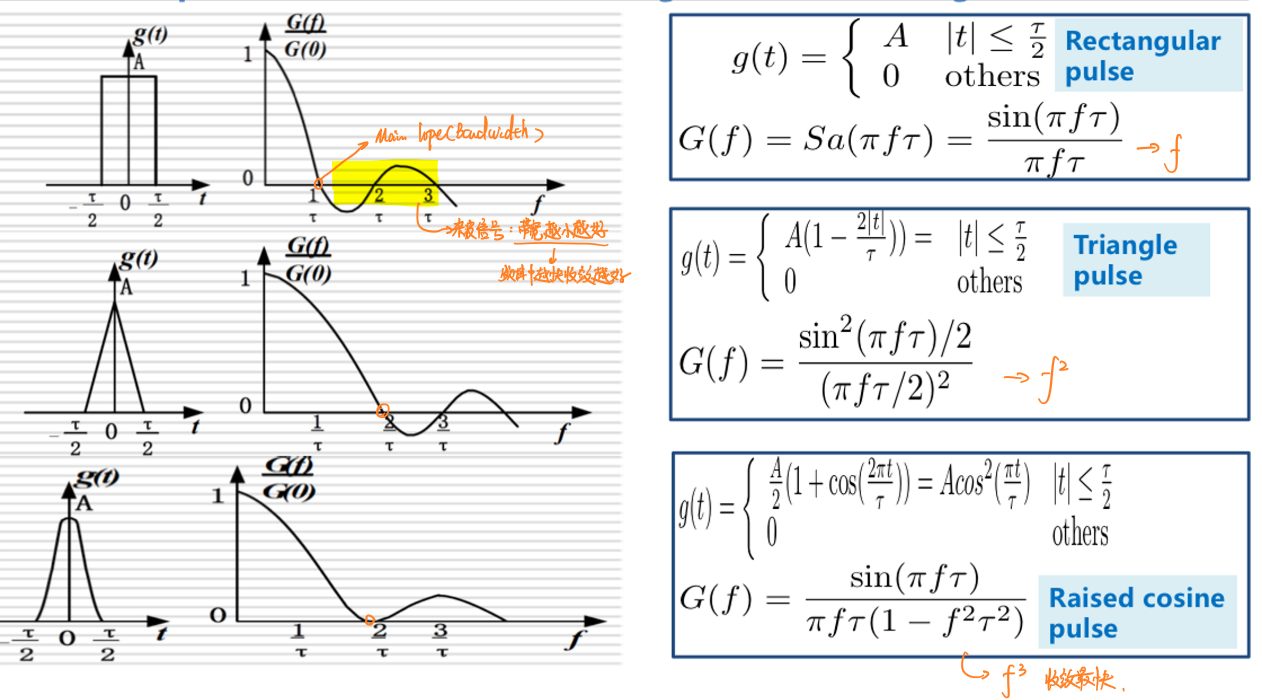
波形选择

对波形的选择标准要求频谱图上的主瓣（即信号的有用带宽）后杂波的带宽越小越好，换言之，频谱函数收敛速度越快越好。 在方波脉冲、三角脉冲、升余弦脉冲中，升余弦脉冲的收敛速度最快，意味着杂波的带宽通常比较小，因此在数字基带通信中常选择升余弦脉冲作为基带波形。
另外，对于归零码而言，符号持续时间越长，占用带宽越小。

消除码间串扰的方式

由于系统的带宽有限，单个字符信号的脉冲发生了失真，使得波形发生延展、含有拖尾，波形延展到其他码元时间间隔中时，会对其他字符的抽样产生干扰，称为码间串扰。码间串扰与系统的带宽有关，系统的带宽越小，字符脉冲的拖尾就会越长越严重，发生码间串扰的可能性越大。

无码间串扰的数学条件

在时域上表示为在抽样时间之外的其他采样时刻上对应波形的幅度为0。
在频域上满足奈奎斯特第一定律：
当且仅当系统的等效频谱在为一个在\(±\frac{π}{T_s}\)上的门函数时，这个系统可以满足没有码间串扰。
导出结论：
- 满足奈奎斯特第一定律时，频谱图的带宽称为奈奎斯特带宽\(B_N\),\(B_N=\frac{1}{2T_s}Hz\)。
- 奈奎斯特间隔为：\(T_s=\frac{1}{2B_N}\)。
- 当采样周期为奈奎斯特间隔的整数倍（\(T_s=\frac{Const}{2B_N}\)）时，可以使得每次采样时信号拖尾的采样值都为0，系统无码间串扰。对应的数据传输速率为：\(R_B=\frac{1}{nT_s}\)。
- 系统支持的最大的传输速率为\(R_{B|max}=\frac{1}{T_s}=2B_N\)，当且仅当： \[\frac{R_{B|max}}{R_B}=Const\] 时，系统无码间串扰。
- 由频谱利用率\(η=\frac{R_B}{B}\)，系统最大的频谱利用率为\(η=\frac{2B_N}{B_n}=2\)。

理想低通滤波器

理想低通滤波器的频谱正好是一个门函数：

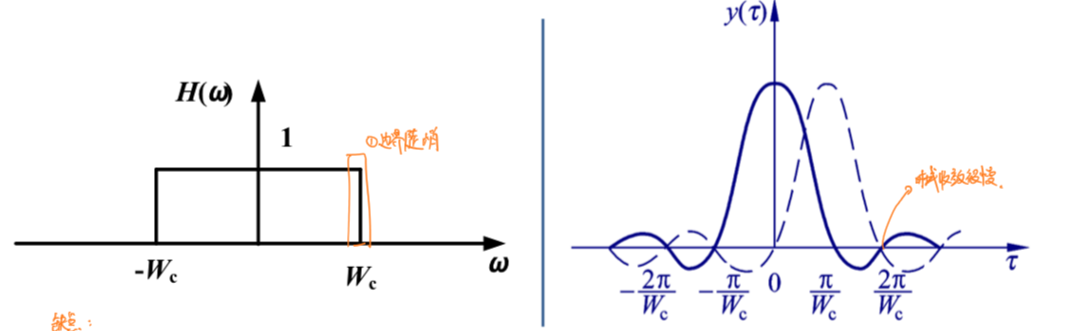
但是，可以从理想低通滤波器系统的频谱和波形图看出：理想低通滤波器有边界陡峭、难以实现、且时域中Sa函数收敛较慢的特点，因此考虑采用其他方法模拟等效理想低通滤波器的频谱。

滚降滤波器

滚降滤波器的基本思路是在理想低通滤波器频谱后加入一段奇对称的频谱，使得被剪切、时移、叠加后的等效频谱中奇对称的一半正好可以填充另一半，得到一个门函数的频谱，这种方法称为滚降。

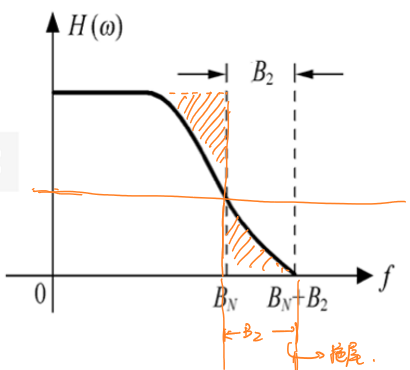
常常被选用的奇函数为反比例函数和升余弦函数（即余弦函数+常数）：

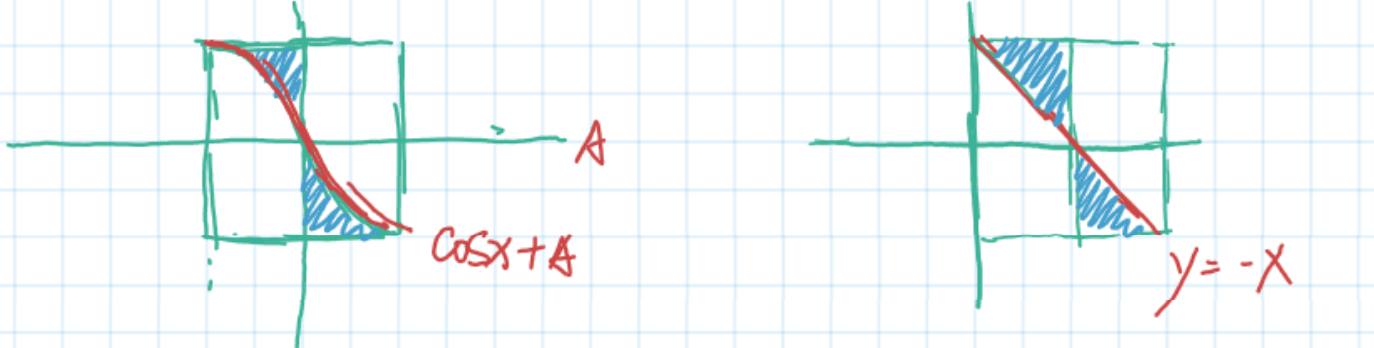
设奇对称信号的带宽为\(B_2\),那么滚降后的系统带宽为\(B_N+B_2\)。
滚降滤波器的系统方程可以表示为： \[H(ω)=\begin{cases} Const, 0≤ω≤B_N\\ f(ω), B_N≤ω≤B_N+B_2\\ 0,ω≥B_N+B_2 \end{cases}\] > 根据系统方程可以将滚降系统的频谱分为：非滚降区、滚降区和截止区。

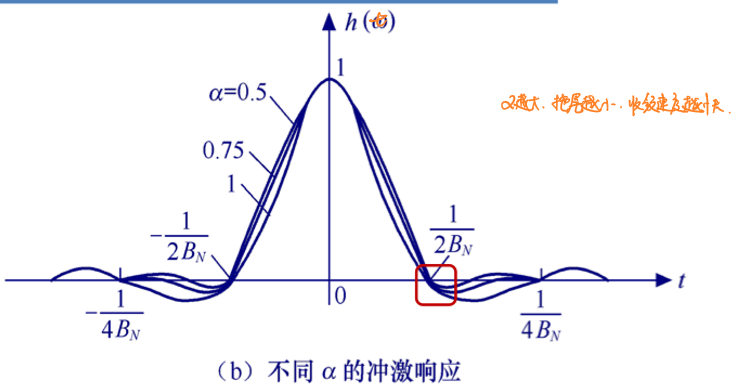
定义滚降系数\(α=\frac{B_2}{B_N}\)，那么系统带宽又可以写作：
\[B=(1+α)B_N,0≤α≤1\] 频谱利用效率为:\(η=\frac{2}{1+α}\)
系统所支持的无码间串扰的最大速率为:\(R_{B|max}=2B_N\) 可以发现，\(α\)越大，系统带宽就越大，系统有效性下降，但是从频谱图上来看，\(α\)越大，系统波形拖尾越小，可靠性上升。

系统类型	\(R_{Bmax}\)	\(B\)	\(η_{max}\)
理想低通滤波器	\(2B_N\)	\(B_N\)	\(2\)
滚降滤波器	\(2B_N\)	\((1+α)B_N\)	\(\frac{2}{1+α}\)
全滚降滤波器	\(2B_N\)	\(2B_N\)	\(1\)
部分响应系统	\(2B_N\)	\(B_N\)	\(2\)

数字基带传输系统的抗噪性

• 使用单极性信号时数字基带传输系统的信噪比： \[SNR_u=\frac{A^2}{2σ^2}\] 误码率为：
  \[P_e=\frac{1}{2}erfc(\frac{\sqrt{SNR_u}}{2})\]
• 使用双极性信号时数字基带传输系统的信噪比： \[SNR_b=\frac{A^2}{σ^2}\] 误码率为：
  \[P_e=\frac{1}{2}erfc(\sqrt{\frac{SNR_b}{2}})\]

数字带通传输系统

ASK

调制方式

有波形时为1，无波形时为0。
输出波形表达式为：
\[S_{2ASK}(t)=\begin{cases} cosω_ct,以概率P\\ 0,以概率1-P\\ \end{cases}\]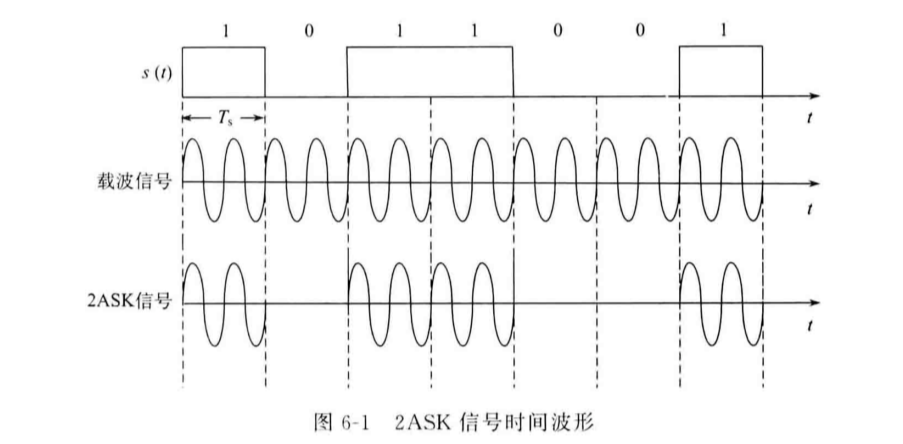

解调方式

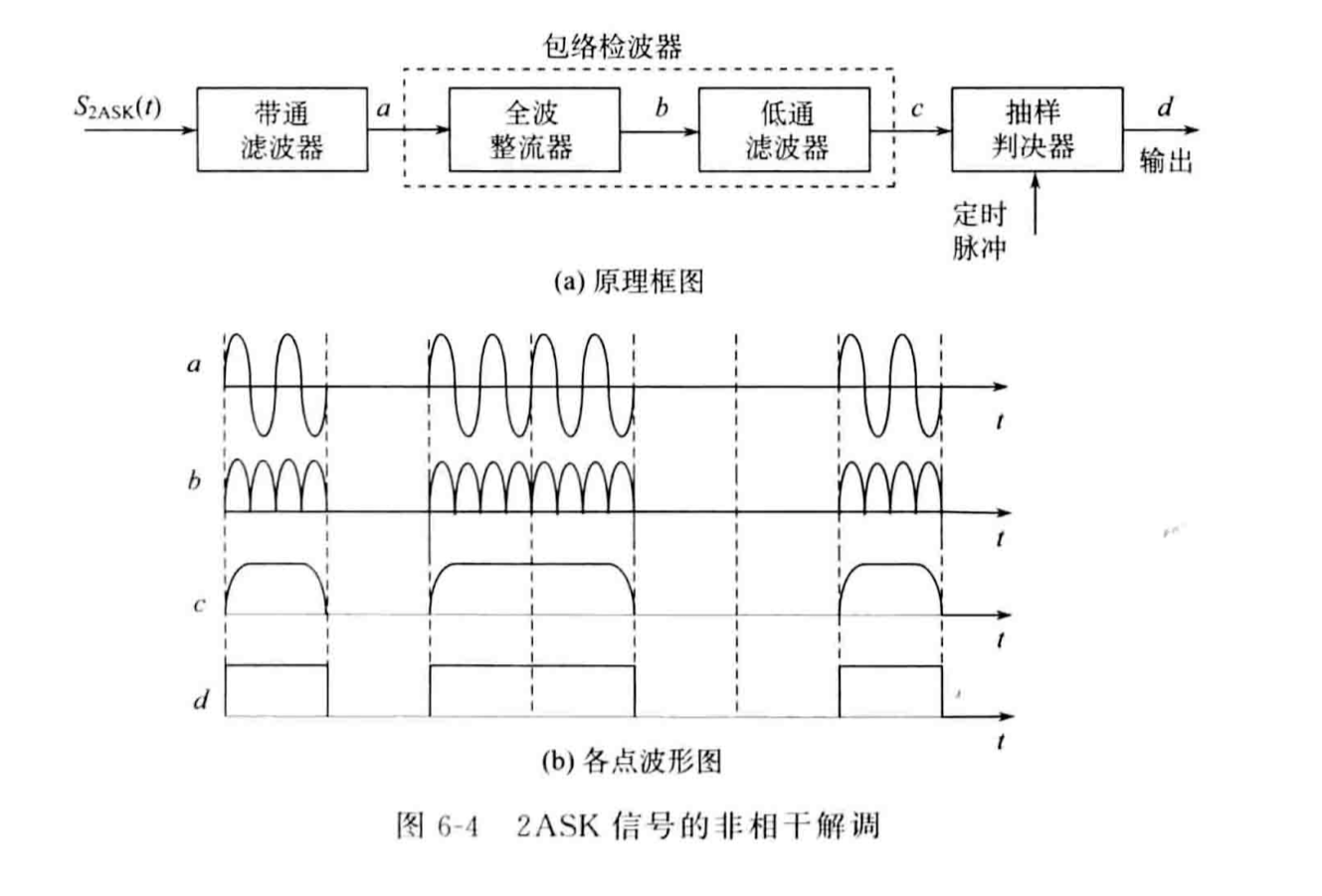
• 非相干解调
  使用包络检波法：使用全波整流器输出信号的绝对值波形以去除极性，然后使用低通滤波器过滤高频分量，最终通过抽样判决器输出数字信号。
  

  注意在模拟信号的解调中，包络检波法不需要全波整流器去除极性，注意区分。

  

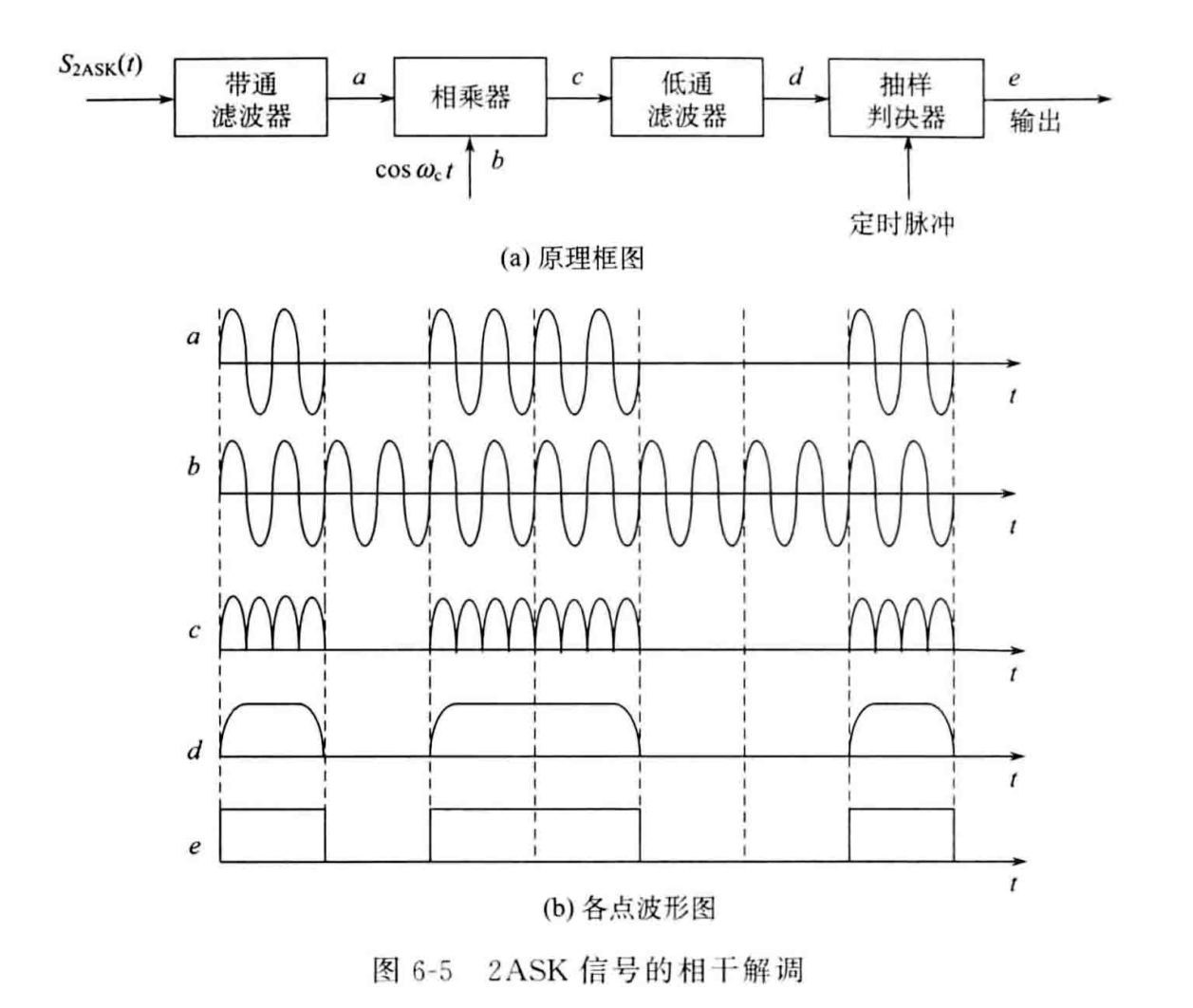
• 相干解调
  使用同频同相的载波与其相乘，通过低通滤波器。
  

FSK

调制方式

FSK使用两个不同频率的载波\(cos(ω_1t)\)、\(cos(ω_2t)\)来表示数字信号“1”和“0”。
输出波形的表达式为：
\[S_{FSK}=[∑_na_ng(t-nT_s)]cos(ω_1t)+[∑_n\overline{a_n}g(t-nT_s)]cos(ω_2t)\]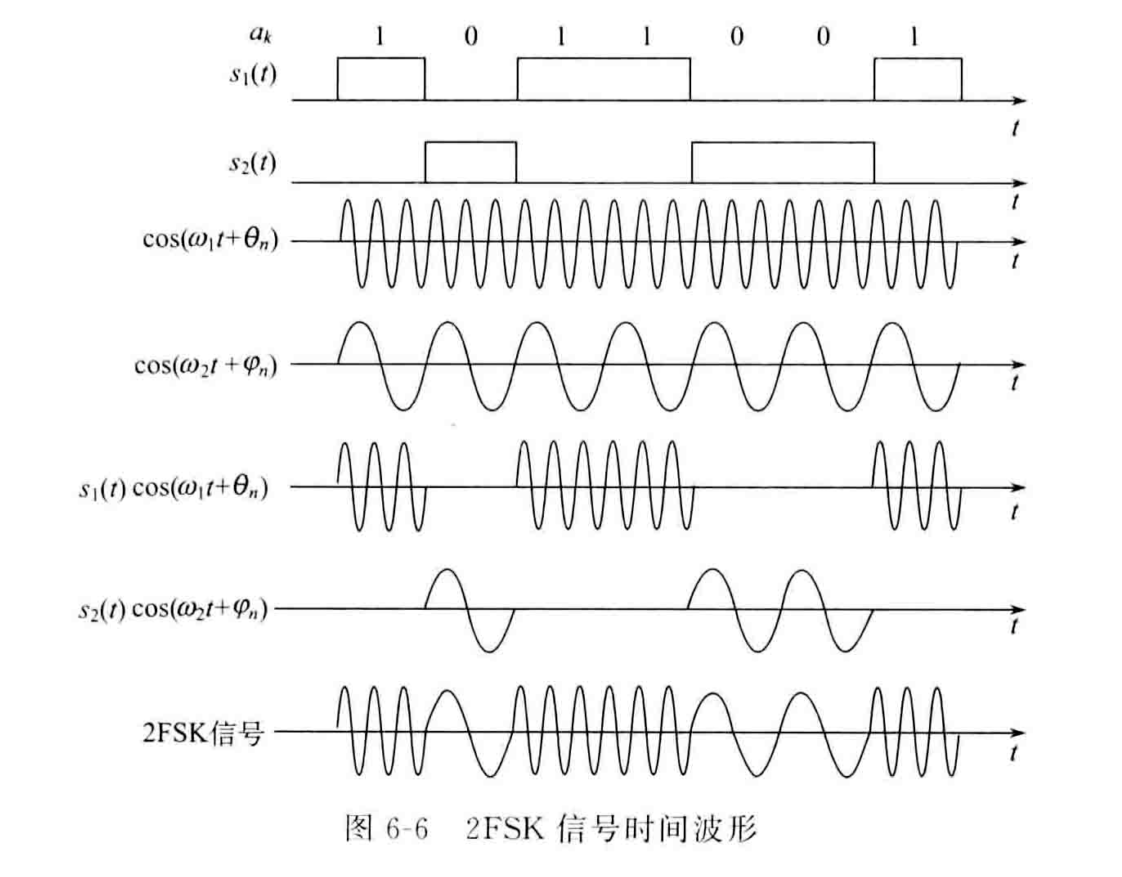

解调方式

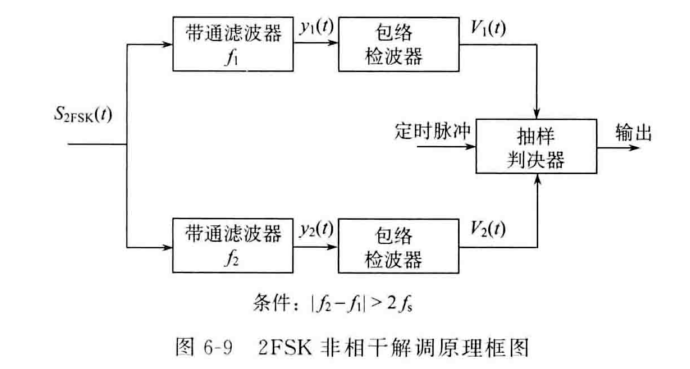
• 非相干解调（包络检波法）
  非相干解调的过程和相干解调基本相同，只不过每一路信号采用包络检波法取代与载波相乘。
  由于仍然需要带通滤波器分别提取两路信号的频谱分量，因此非相干解调也只适用于\(|f_1-f_2|≥2f_s\)的情况。
  抽样判决的过程和相干解调相同，也不需要设置判决门限。
  

• 相干解调
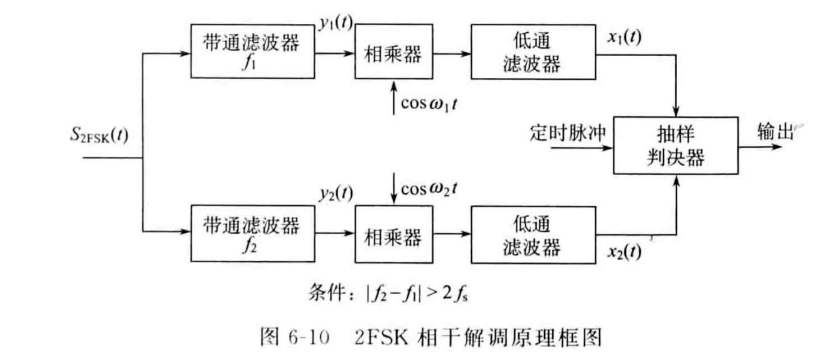
  在接收端，FSK信号\(S_{2FSK}(t)\)分为两路，各通过一个带通滤波器，只过滤出\(f_1\)或者\(f_2\)的频谱分量，每一路信号在通过带通滤波器之后与对应的同频同向的载波信号相乘去除极性，通过低通滤波器过滤掉高频分量后，送入抽样判决器进行判决。
  只有在\(f_1\)和\(f_2\)的连续谱分量完全分离时，带通滤波器才能准确提取出对应频率的分量，因此相干解调只适用于\(|f_1-f_2|≥2f_s\)的情况。
  抽样判决器的判决标准是两路信号在同一个码元周期\(T_s\)内的电平大小进行比较，哪路信号的电平高，则数字信号的值就为这一路所代表的逻辑值。因此，相干解调不需要设置判决门限。
  

• 过零检波法
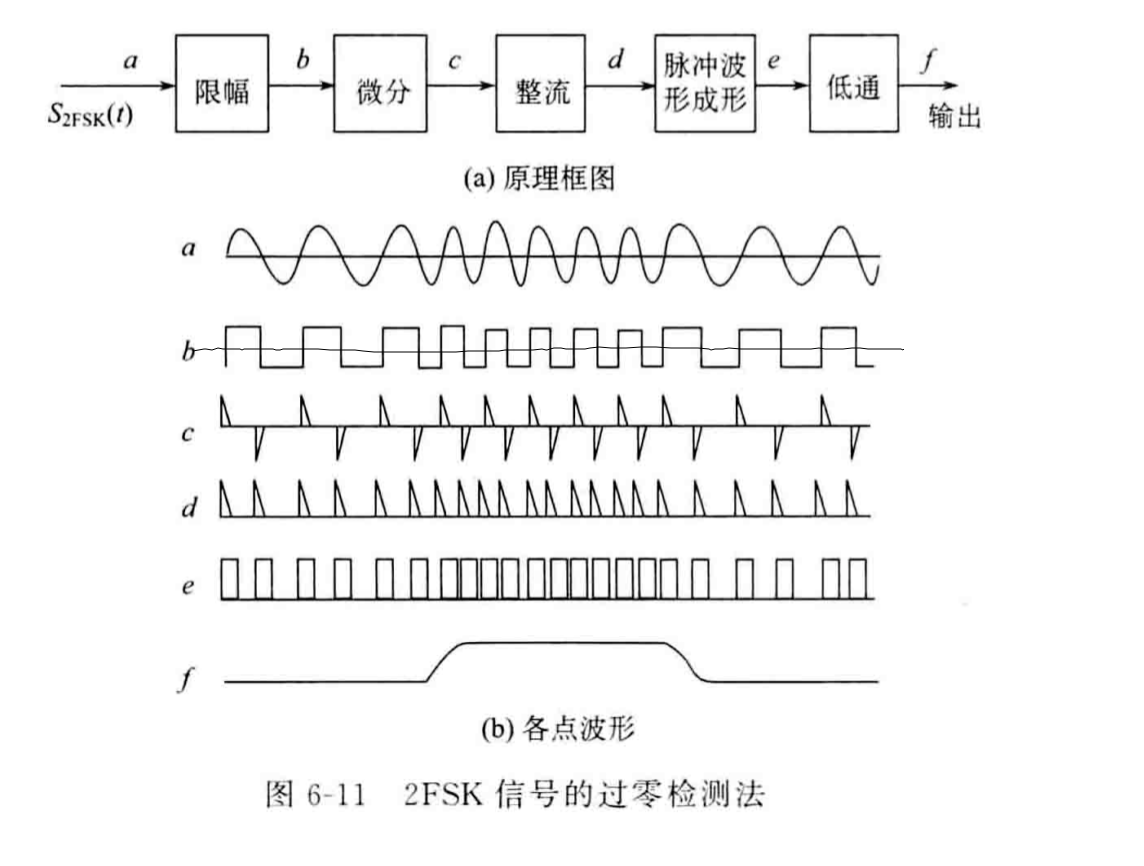
  非相干解调和相干解调都只适用于\(|f_1-f_2|≥2f_s\)的情况，而过零检波法没有这样的条件限制。
  过零检波法的原理是：在波形图上波形过0的次数越多代表码元周期内的频率越高，过零检波法的基本思路是用码元周期内平均幅度的大小来表示频率的高低。
  > 方波脉冲信号的直流分量：\(\frac{1}{T_s}∑τ_iA_i,τ_i\)为周期内第\(i\)个方波脉冲的持续时间。

过零检波法的具体过程是：FSK信号首先通过限制幅度将正弦波转变为方波，方波通过微分器后变为脉冲信号，经过整流器去除极性后，再用宽脉冲发生器依据脉冲信号重新生成无极性的方波信号。
方波信号会通过低通滤波器，低通滤波器只会允许低频分量（在此看做只有直流分量可以通过）通过滤波器，在单个码元周期中，方波脉冲的个数越多，代表其平均幅度越大，根据直流分量代表波形中的平均幅度可知，其直流分量也会更大。因此原波形中高频的部分通过低通滤波器之后的直流分量更大，低频部分通过低通滤波器后的直流分量更小。

最后信号通过抽样判决器，抽样判决器的最佳判决门限为\(\frac{a}{2}\)。

PSK

调制方式

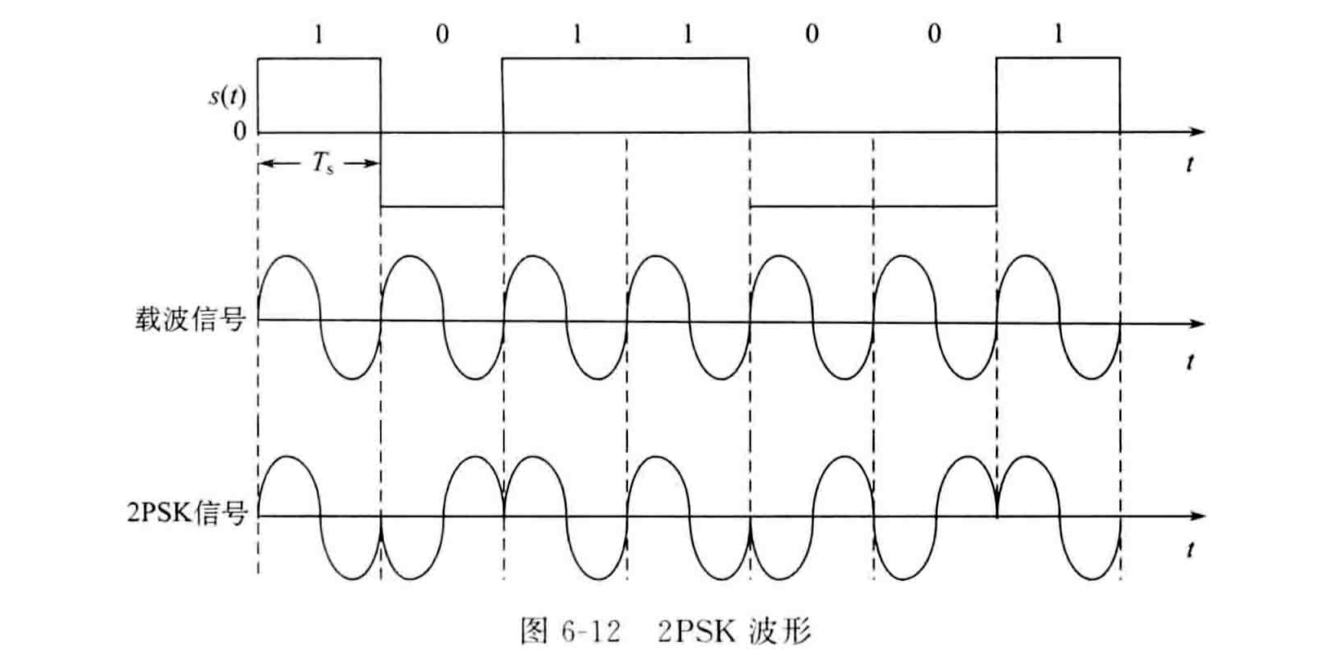
PSK使用两个反相的载波\(Acos(ω_ct)\)和\(-Acos(ω_ct)\)表示数字信号“1”和“0”。
PSK信号的波形可以表示为： \[S_{2PSK}(t)=∑_nb_ng(t-nT_s)cos(ω_ct)\] \(b_n\)是\(a_n\)的双极性码表达。

解调方式

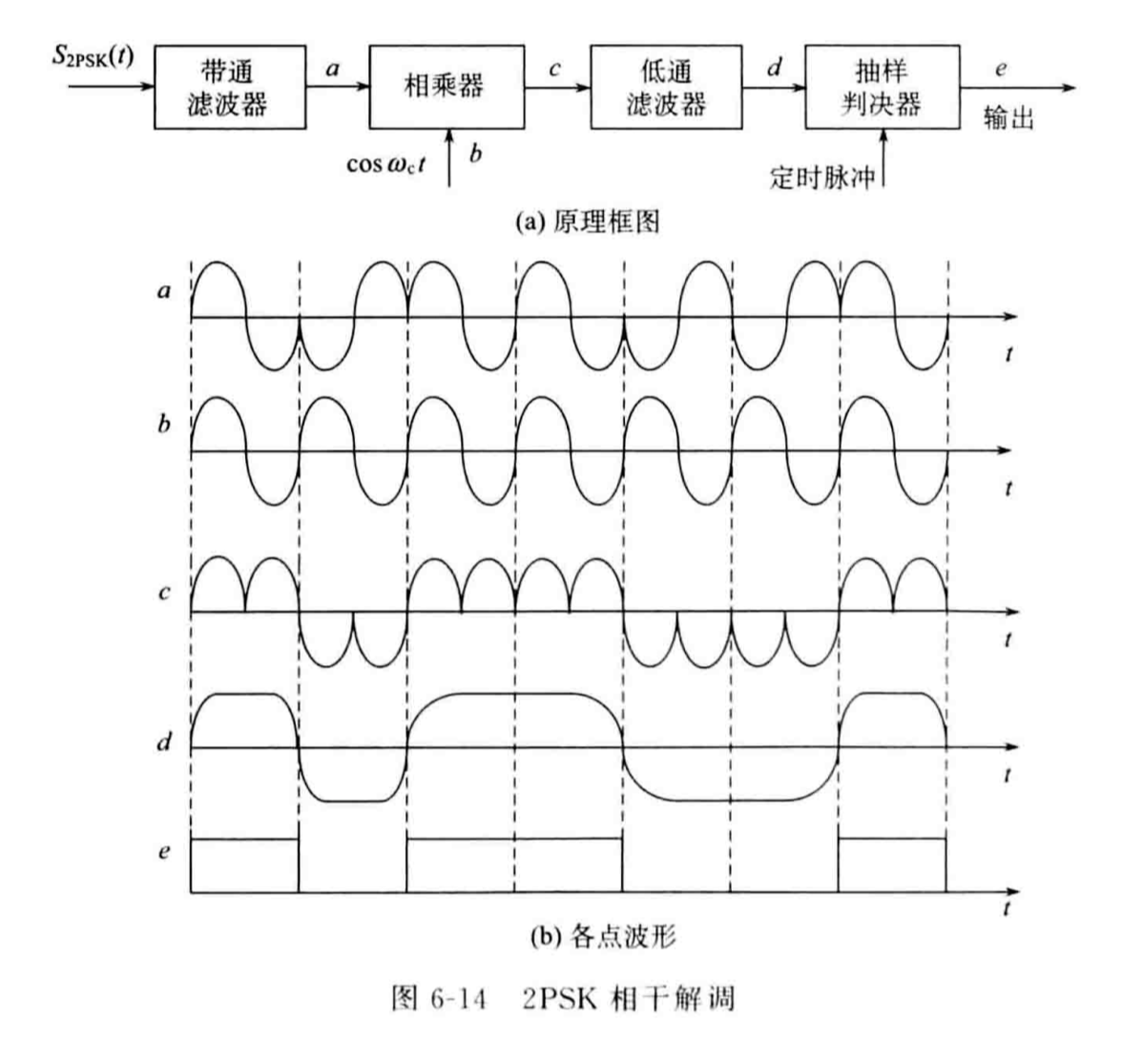
• 相干解调
  

  由于PSK信号通过全波整流器后各个码元周期内的信号完全相同，无法辨认“0”或“1”，因此PSK信号不能使用非相干解调，只能使用相干解调。

  在相干解调中，PSK信号通过带通滤波器后和同频同向的载波相乘，表示“-1”的波形与载波相乘，得到的波形会完全在小于0的一侧，表示“1”的波形与载波相乘，得到的波形会完全在大于0的一侧。信号通过低通滤波器消除高频分量后送入抽样判决器进行判别。抽样判决器的最佳判决门限为0。
  

DPSK

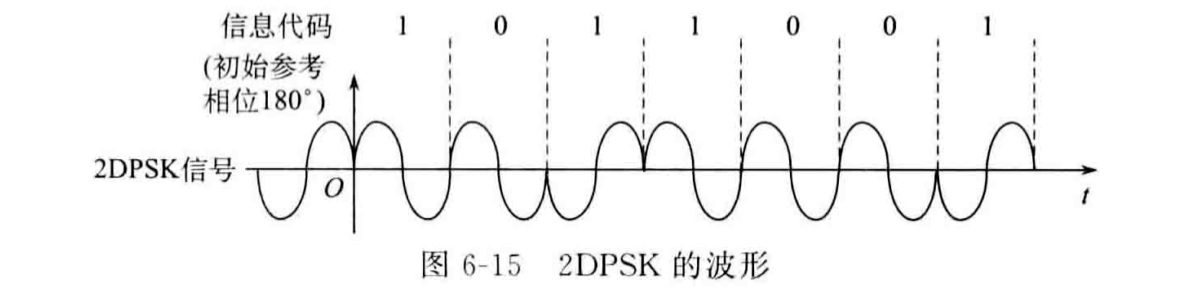
调制方式

传统的PSK在解调过程中需要依赖未调制载波\(cosω_ct\)的相位，如果载波相位发生反转，调制结果会随之发生反转，这种现象称为倒π现象。
为了解决倒π现象以及相位模糊（Phase ambiguity）问题，DPSK（相对相移键控）选择使用相对码来取代PSK中使用的绝对码，以使得解调结果不依赖\(cosω_ct\)的相位。
DPSK的具体做法是:假设\(b_n\)为\(a_n\)的差分码，有： \[b_n=a_n⊕b_{n-1} \] 即当前差分码\(b_n\)是前一个差分码\(b_{n-1}\)与当前绝对码\(a_n\)的模二加法（异或）结果。
再将差分码做PSK调制即可。

解调方式

• 相干解调
  同PSK相干解调

• 差分解调
  除了使用同频同相的载波与DPSK信号相乘外，还可以使用延时一个码元周期的原DPSK信号与自身信号相乘，两者都能够达到“表示-1的波形与载波相乘，得到的波形会完全在小于0的一侧，表示1的波形与载波相乘，得到的波形会完全在大于0的一侧。”的效果。
  

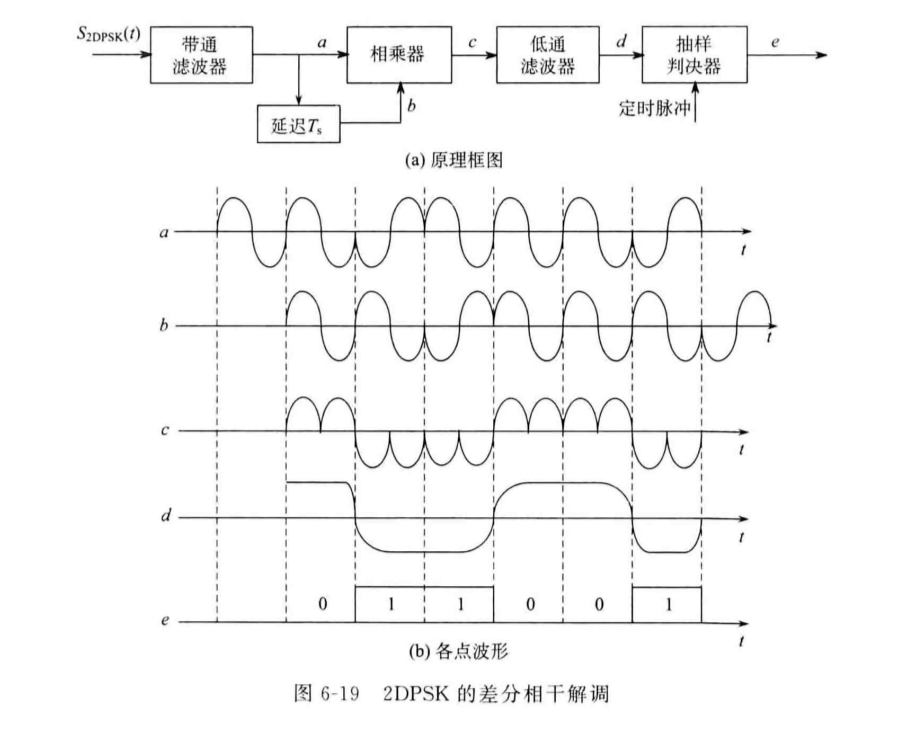
实际设计中往往采用差分解调，原因是差分解调中所使用的延时模块成本比相干解调中用于产生本地载波的振荡器成本更低。

调制方式	受调信号的码型	受调信号的带宽	解调方法	解调的最佳判决门限
ASK	单极性码	\(2B_s\)	相干解调 包络检波法	\(\frac{a}{2}\)
FSK	单极性码	\(\lvert f_1-f_2\rvert +2B_s\)	相干解调 包络检波法 过零检波法	无 无 \(\frac{a}{2}\)
PSK	双极性码	\(2B_s\)	相干解调	0
DPSK	双极性码	\(2B_s\)	相干解调 相位比较法	0

数字调制方式的性能对比

• 抗噪性
  \[PSK>DPSK>FSK>ASK\] \[相干解调>非相干解调\]
• 信噪比
  系统的误码率下降时，系统的信噪比上升。
• 有效性
  ASK/PSK和DPSK的带宽相同，FSK的带宽大于前三者，因此FSK的频谱利用效率最低，有效性最差，其余三者相同： \[ASK=PSK=DPSK>FSK\]

调制方式	受调信号的码型	受调信号的带宽	解调方法	解调的最佳判决门限	最大频谱利用效率	误码率
ASK	单极性码	\(2B_s\)	相干解调 包络检波法	\(\frac{a}{2}\)	\(\frac{1}{2}\)	\(\frac{1}{2}erfc(\frac{\sqrt{SNR}}{2})\) \(\frac{1}{2}e^{-\frac{SNR}{4}}\)
FSK	单极性码	\(\lvert f_1-f_2\rvert +2B_s\)	相干解调 包络检波法 过零检波法	无 无 \(\frac{a}{2}\)	\(\frac{R_B}{\lvert f_1-f_2\rvert +2R_B}\)	\(\frac{1}{2}erfc(\sqrt{\frac{SNR_{FSK}}{2}})\) \(\frac{1}{2}e^{-\frac{SNR_{FSK}}{2}}\)
PSK	双极性码	\(2B_s\)	相干解调	0	\(\frac{1}{2}\)	\(\frac{1}{2}erfc(\sqrt{SNR_{PSK}})\)
DPSK	双极性码	\(2B_s\)	相干解调 相位比较法	0	\(\frac{1}{2}\)	\(\frac{1}{2}e^{-SNR_{PSK}}\)

所有调制方法的信噪比均为： \(SNR=\frac{\frac{a^2}{2}}{2n_0B_{S}}\)。