10. FIR滤波器设计方法

FIR滤波器设计方法

在实际的滤波器设计中，需要通过各种各样的方法来近似理想滤波器的幅度值响应，从而近似实现理想滤波器的功能。

加窗法

加窗法（Windowing）基于离散时间傅里叶变换（DTFT）进行设计，其基本思想是由于理想滤波器的带宽是无限长的，通过截取理想滤波器系统冲激响应的一段序列，并用窗函数序列加权来替代整个理想滤波器的波形。

实现流程

加窗法的实现依赖于理想低通滤波器，理想低通滤波器的冲激响应为：
\[h[n]=\frac{sin(ω_cn)}{πn}\] 其中\(ω_c\)表示其截止频率。
1. 设置滤波器的长度\(L=2N+1\)，并在理想低通滤波器冲激响应上截取\(L\)个采样点。为了满足线性相位滤波器的条件，通常使用以\(h[0]\)为对称轴的奇数\(L\)个序列。定义滤波器的阶数\(M\)为滤波器序列长度减一： \[M=L-1\] 此时的序列为\(\{h[-N],h[-N+1],..,\underset{n=0}{h[0]},..,h[N-1],h[N]\}\),是一个非因果序列。 2. 对截取的序列做时移以满足系统的因果性，时移量为\(α=\frac{L-1}{2}=N\)，称为滤波器的群时延(Group delay)。
此时的序列为：\(\{\underset{n=0}{h[-N]},h[-N+1],..,h[0],..,h[N-1],h[N]\}\) 3. 为了使得滤波器性能更好，还需要对产生的序列进行赋权，产生赋权序列的函数称为窗函数（Window function），赋权的操作为： \[fl[n]=h_d[n]×w[n]\] 其中\(h_d[n]\)为截取和时移之后的理想低通滤波器序列，\(w[n]\)由窗函数产生，对于矩形窗：\(w[n]=1\)，之后会对窗函数做更加详细的介绍。

需要注意的是，窗函数的阶数比序列阶数高2，再截掉窗函数序列两端的0后，与理想低通滤波器序列相乘。

加窗法的频谱分析·滤波器波形的影响因素

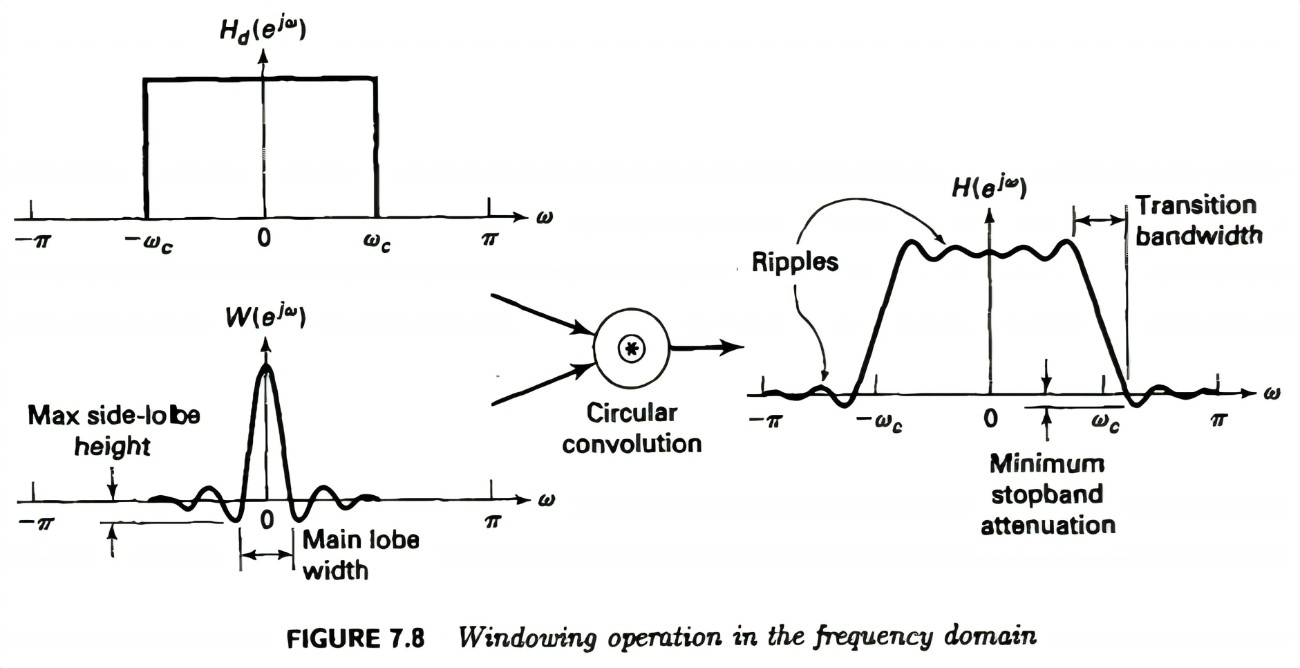
在频域中，赋权表示为实际滤波器\(h_d[n]\)的频率响应与窗函数频率响应的周期卷积：
\[fl(e^{jω})=H_d(e^{jω}) \tilde{⊕} W(e^{jω})\] 在频域中\(H_d(e^{jω})\)是一个门函数，对矩形窗，\(W(e^{jω})\)是采样函数。
两者周期卷积的过程如下图所示：

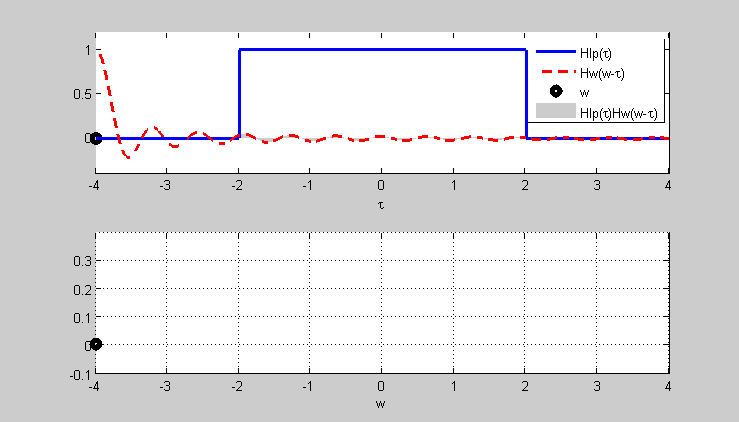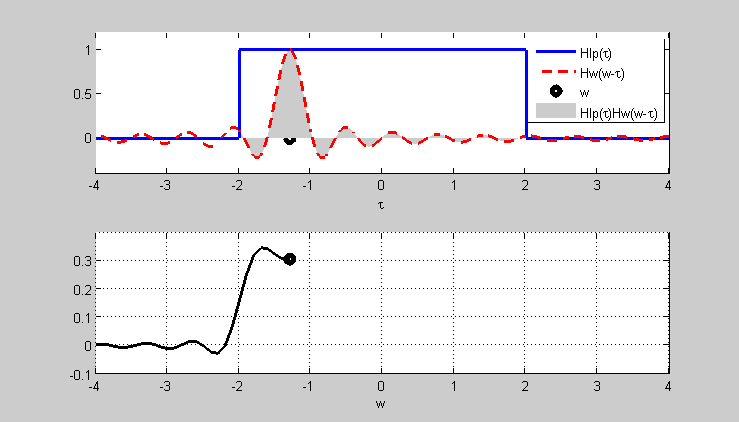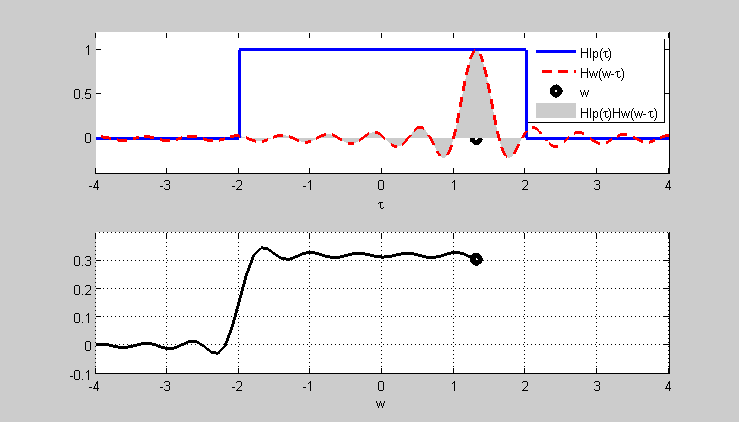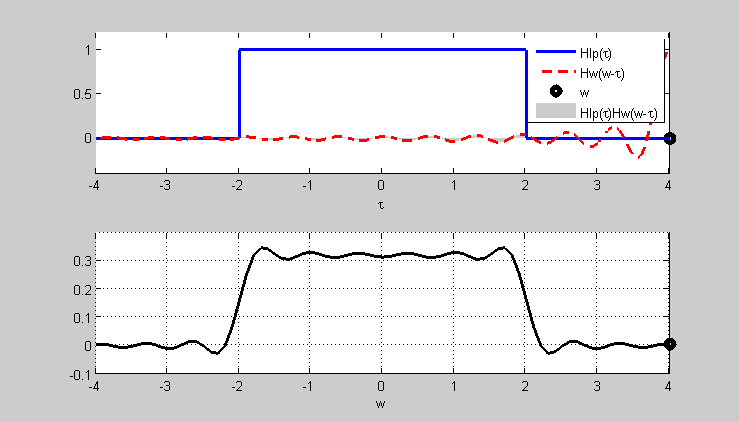
两者的卷积结果如下图所示：

波纹

可以发现，由于窗函数旁瓣在频域上的振荡，使得卷积后的频率响应中在通带和止带都出现了振荡，称为滤波器的波纹(Ripple)。同时可以发现，波纹在周期卷积过程中的形成只和窗函数频谱的主瓣和旁瓣的相对幅值有关，定义峰值旁瓣比(PSLR，peak side lobe ratio) 表示dB化后的主瓣相邻旁瓣幅值和主瓣幅值之比： \[r_p|dB=20lg(\frac{A_{sidelope}}{A_{mainlope}})\] 可以发现，窗函数频谱中峰值旁瓣比越小，波纹的振荡就越小。

过渡带带宽

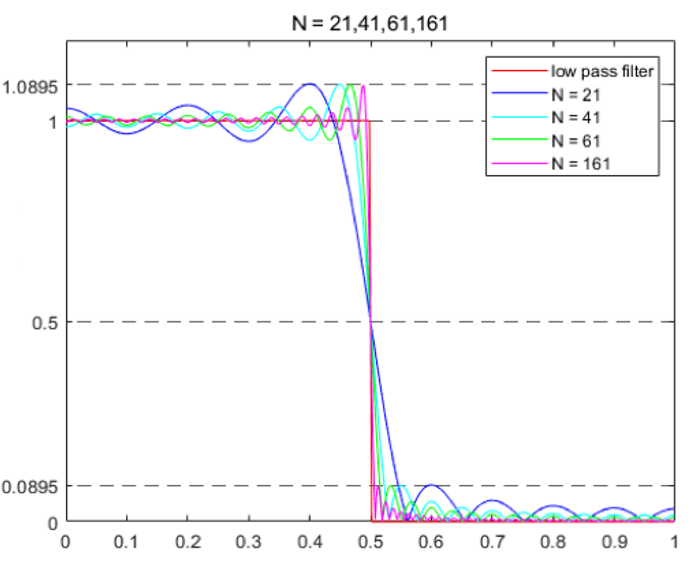
由上图可以看出，采样点的个数和过渡带带宽成反比关系。 并且，过渡带带宽为主瓣带宽。
增大采样点的个数（实际设计中增大抽头数\(N\)），其过渡带会减小。

吉布斯效应

同时，增大抽头数\(N\)还会改变波纹的密度，抽头数增多，其波纹密度增大 ，但是每个波纹的幅值并不会改变，这个效应称为吉布斯效应。 吉布斯效应可以通过设计窗函数时让窗函数的时域表达平缓的由1减小到0来消除。

宽容度

上述影响因素都是基于幅度值-频率响应得出的，定义滤波器的幅度-频率响应为：
\[A_e(e^{jω})=H_e(e^{jω}) \tilde{⊕} W_e(e^{jω})\] 对于第一类FIR滤波器(序列对称，长度为奇数)，有：
\[A_e(e^{jω})=H(e^{jω})e^{-jαω}\] \(H\)和\(W\)为原始滤波器和窗函数的幅度-频率响应。
低通滤波器的幅度响应图如下：

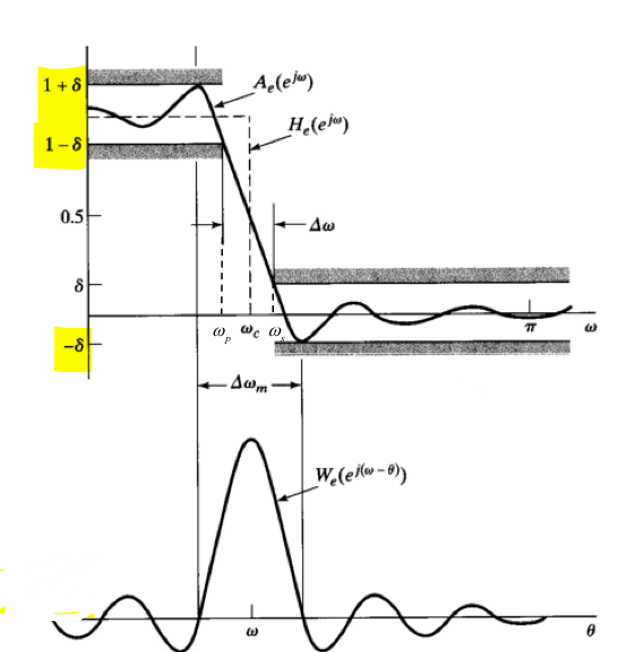
定义波纹偏离1或0的最大幅值为滤波器的宽容度(Tolerance)\(δ\)，上下波纹的宽容度相同。峰值近似误差（Peak approximation error）用dB表示波纹的宽容度：
\[e_p=20lgδ\]

常见窗函数

矩形窗

矩形窗函数： \[w[n]=\begin{cases} 1, 0 ≤n≤N-1\\ 0, otherwise \end{cases}\] 矩形窗函数的峰值旁瓣比：\(r_p=-13dB\)
主瓣宽度\(Δω_m=\frac{4π}{N}\)
由于矩形窗从1到0的变化过快，因此难以消除吉布斯效应。

三角窗

三角窗函数：
\[w[n]=\begin{cases} \frac{2n}{M}, 0≤n<\frac{M}{2}\\ 2-\frac{2n}{M}, \frac{M}{2}≤n≤M\\ 0, otherwise \end{cases}\] 矩形窗函数的峰值旁瓣比：\(r_p=-27dB\)
主瓣宽度\(Δω_m=\frac{8π}{N}\)

汉宁窗（Hanning）

汉宁窗函数：
\[w[n]=0.5-0.5cos(\frac{2πn}{M}),0≤n≤M\] 矩形窗函数的峰值旁瓣比：\(r_p=-31dB\)
主瓣宽度\(Δω_m=\frac{8π}{N}\)

汉明窗（Hamming）

汉宁窗函数：
\[w[n]=0.54-0.46cos(\frac{2πn}{M}),0≤n≤M\] 矩形窗函数的峰值旁瓣比：\(r_p=-41dB\)
主瓣宽度\(Δω_m=\frac{8π}{N}\)

布莱克曼窗（Blackman）

布莱克曼窗函数：
\[w[n]=0.42-0.5cos(\frac{2πn}{M})+0.08cos(\frac{4πn}{M}),0≤n≤M\] 矩形窗函数的峰值旁瓣比：\(r_p=-57dB\)
主瓣宽度\(Δω_m=\frac{12π}{N}\)

凯撒窗

凯撒窗函数：
\[w[n]=\begin{cases} \frac{I_0[β(1-[\frac{n-α}{α}]^2)^{\frac{1}{2}}]}{I_0(β)},0≤n≤M\\ 0, otherwise \end{cases}\] 凯撒窗的过渡带带宽由凯撒窗的阶数和宽容度决定：
\[M=\frac{-e_p-8}{2.285Δω}\] 宽容度由形状参数决定：
\[β=\begin{cases} 0.1102(-e_p-8.7),-e_p>50\\ 0.5842(-e_p-21)^{0.4}+0.07886(-e_p-21),21≤-e_p≤50\\ 0, -e_p<21 \end{cases}\] 凯撒窗可以通过控制阶数和形状参数\(β\)来控制宽容度和过渡带带宽。
对于给定宽容度和过渡带带宽的设计要求，应用凯撒窗函数设计滤波器的步骤：
1. 根据宽容度\(δ\)计算出\(e_p\)
2. 根据\(e_p\)计算出\(β\)。
3. 根据\(e_p\)和过渡带带宽计算出凯撒窗的阶数。

高通和带通、带阻滤波器设计

高通和带通、带阻滤波器的频率响应都可以通过对低通滤波器频率响应加以一定的数学变换得到。
#### 高通滤波器 高通滤波器的频率响应可以表示为1-低通滤波器：
\[H_{HP}(e^{jω})=1-H_{LP}(e^{jω})\] 对应时域冲激响应表示为：
\[h[n]=δ[n]-\frac{sin(ω_cπ(n-α))}{πn}\]

带通滤波器

带通滤波器的频率响应可以表示为两个截止频率不同的低通滤波器频率响应相减：
\[H_{BP}(e^{jω})=H_{LP1}(e^{jω})-H_{LP2}(e^{jω})\] 对应时域冲激响应表示为：
\[h[n]=\frac{sin(ω_{ca}π(n-α))}{πn}-\frac{sin(ω_{cb}π(n-α))}{πn}\]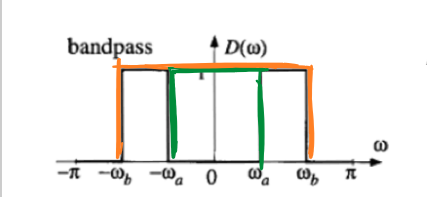

带阻滤波器

带阻滤波器的频率响应可以表示为1-带通滤波器的频率响应。
\[H_{HP}(e^{jω})=1-H_{LP}(e^{jω})\] 对应时域冲激响应表示为：
\[h[n]=δ[n]-\left(\frac{sin(ω_{ca}π(n-α))}{πn}-\frac{sin(ω_{cb}π(n-α))}{πn}\right)\]

使用MATLAB进行滤波器设计

MATLAB中，可以使用fir1()函数来进行加窗法的程序设计，其具体表达为：
fir1(order,omega_c,filtertype,windowtype,"noscale/scale")
其中order表示滤波器的阶数；omega_c是π归一化后的滤波器截止频率；filtertype表示设计的滤波器类型，缺省值为低通滤波器"low"；windowtype表示使用的窗函数，缺省值为海宁窗；"noscale/scale"表示是否需要归一化。
其中常见的窗函数有：
- boxcar(l)：矩形窗
- hann(l)：海宁窗
- kaiser(l,beta)：凯撒窗
l 表示的是滤波器的序列长度，注意与滤波器的阶数作区分。

fir1()函数会返回滤波器的冲激响应序列，返回的冲激序列使用[H_f,w]=freqz(h)返回其幅度-频率响应H_f和角频率轴w。
其幅度值-频率响应可以通过求其绝对值abs(H_f)得到，相频响应可以通过angle(H_f)得到。
下面的例程展示了如何用MATLAB绘制一个序列长度为7，截止频率为0.5π的理想低通滤波器：

h = fir1(6, 0.5, "low",boxcar(7),"noscale"); % generate the filter
[hf,w] = freqz(h); % 频率响应
figure(1);
plot(w/pi,abs(hf)); % 幅频响应
xlabel("\omega / \pi")
title("Magnitude response");
figure(2);
plot(w/pi,angle(hf)); % 相频响应
xlabel("\omega / \pi");
title("Phase response");

下面例程用于生成一个序列长度131，截止频率0.5π，β=4.966的凯撒窗低通滤波器，例程如下：

% 生成一个序列长度131，截止频率0.5π，β=4.966的凯撒窗滤波器
h = fir1(130, 0.5, "low",kaiser(131,4.966),"noscale"); 
[hf,w] = freqz(h); % 幅度-频率响应
figure(1);
plot(w/pi,abs(hf)); % 幅度值-频率响应
xlabel("\omega / \pi")
title("Magnitude response");
figure(2);
plot(w/pi,angle(hf)); % 相频响应
xlabel("\omega / \pi");
title("Phase response");

频率采样法*

频率采样法的核心思想是滤波器的冲激响应\(h[n]\)的离散傅里叶变换的本质是对其频率响应\(H(e^{jω})\)进行采样。采样后通过在每个采样点之间插值，来近似拟合滤波器的频率响应。
因此，对于给定的理想滤波器频率响应\(H(e^{jω})\)，其对应的离散傅里叶变换应当为：
\[H(e^{jω})|_{ω=\frac{2πk}{N}}=H[k]\] \(H(e^{jω})\)中\(\frac{N-1}{2}\)的序列通过采样生成后做对称生成后半部分的序列，以满足滤波器的线性相位特性。
最后，对整个序列做群时延\(α=\frac{N-1}{2}\)以满足因果性。即可生成实际的滤波器序列。

优化方法*

相当多的通信调制方法中对于滤波器的波纹要求很高，因此需要对滤波器函数做进一步的优化，优化的基本思想是对滤波器的波纹进行赋权，权值函数为\(w_{rp}[n]\)，使得滤波器在频域上的表现更加接近于理想滤波器。
定义滤波器优化方法的损失函数为：
\[ϵ^2=\frac{1}{2π}∫_{-π}^π\lVert W_{rp}(e^{jω})\left(H_d(e^{jω})-H(e^{jω})\right)\lVert ^2dω\] 其中，\(H_d(e^{jω})\)是实际设计的滤波器的频率响应，\(H(e^{jω})\)对应理想滤波器的频率响应。
基本上所有的优化方法的思路都是寻找损失函数取得最小值时所对应的权重\(W_{rp}\)。
常见的优化算法有：帕克斯-麦克莱伦算法（Parks–McClellan algorithm）或者梯度下降算法（Gredient Desent），都是寻找全局最小值问题的常用方法，在此不做过多介绍。