11. IIR滤波器设计方法

IIR滤波器设计方法

IIR系统的频率响应：
\[H(z)=\frac{∑_{k=0}^Mb_kz^{-k}}{∑_{k=0}^Na_kz^{-k}}\] IIR滤波器设计的基本思路是通过对模拟滤波器进行参数调整，再通过数字采样将模拟滤波器转换为数字滤波器。

模拟滤波器原型

IIR滤波器设计的两种基本原型是巴特沃斯低通滤波器和切比雪夫低通滤波器，两种滤波器的幅频特性都不含有相位信息，因此IIR滤波器的相位不可控。
这两种滤波器的幅频特性如图所示：

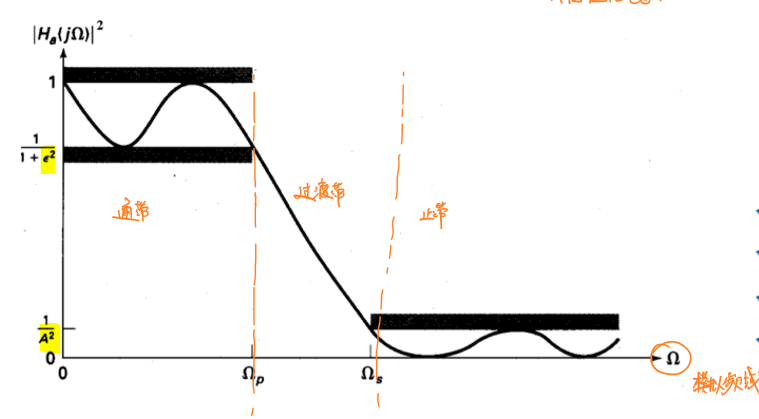
其幅度的模的平方与频率的关系表示为：
\[\frac{1}{1+ϵ^2}≤\lvert H_a(jΩ)\lvert ^2≤1,\lvert Ω \lvert≤Ω_p\] \[0≤\lvert H_a(jΩ) \lvert^2≤\frac{1}{A^2},\lvert Ω \lvert≥Ω_s\] 其中\(ϵ\)称为通带波纹系数，\(Ω_p\)是通带截止频率，\(A\)是止带衰减系数，\(Ω_s\)是止带截止频率。
在通带截止频率时：
\[\lvert H_a(jΩ) \lvert^2=\frac{1}{1+ϵ^2}\] 在止带截止频率时：
\[\lvert H_a(jΩ)\lvert^2=\frac{1}{A^2}\] 定义其通带波纹\(R_p\)为：
\[R_p\lvert_{dB}=-10lg\lvert H_a(jΩ_p)\lvert^2=-10lg\frac{1}{1+ϵ^2}\] 止带衰减\(A_s\)为：
\[A_s=-10lg\lvert H_a(jΩ_s)\lvert^2=-10lg\frac{1}{A^2}\]

巴特沃斯滤波器

巴特沃斯滤波器的特点是在通带和止带都没有波纹，但是过渡带相对较大。巴特沃斯滤波器的幅频响应表示为：
\[\lvert H_a(jΩ) \lvert^2=\frac{1}{1+(\frac{Ω}{Ω_c})^{2N}}\] 其中\(N\)称为巴特沃斯滤波器的阶数，\(ω_c\)为其截止频率，知道这两个参数便可以确定一个巴特沃斯滤波器。

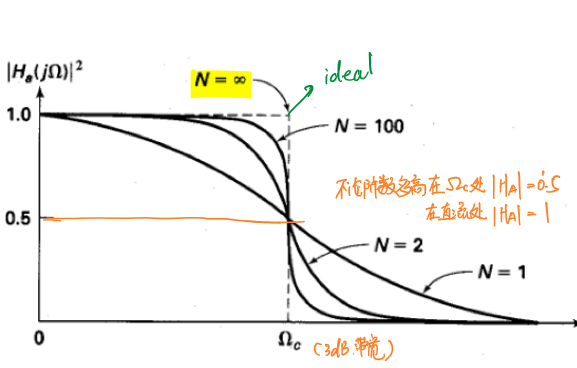
从图中可以发现，阶数越高，巴特沃斯滤波器的过渡带宽越窄，\(N→∞\)时成为理想低通滤波器。同时，无论任何阶数，其截止频率下\(\lvert H_a(jΩ_c) \lvert^2=\frac{1}{2}\)。

巴特沃斯滤波器的s域分析

在s域下，由拉普拉斯变换中定义\(Ω=\frac{s}{j}\)，其幅频响应可以写作：

\[\begin{aligned} \lvert H_a(jΩ) \lvert^2&=H_a(s)H_a(-s) \\ &=\frac{1}{1+(\frac{s}{jΩ_c})^{2N}}\\ &=\frac{(jΩ_c)^{2N}}{(jΩ_c)^{2N}+s^{2N}} \end{aligned}\]

求得极点为： \[p_k=Ω_ce^{j\frac{kπ}{N}},k=0,1,...,2N-1\]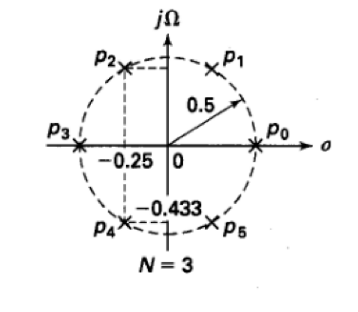

即在幅频响应中令\(Ω=\frac{s}{j}\)，带入后得到\(\lvert H_a(jΩ)\lvert^2=\frac{1}{1+(\frac{s}{jΩ_c})^{2N}}=H(s)H(-s)\)，令下方为0后得到的\(1+(\frac{s}{jΩ_c})^{2N}=0\)的方程解。

可以发现2N个极点均匀的分布在半径为\(Ω_C\)的圆上，由于只有s域左半部分表示稳定一同，因此只选取位于s域左半部分的极点构建滤波器。

由于其所有的极点在s域以\(Ω_c\)为半径的圆上均匀分布，因此极点可以根据下图快速求得：

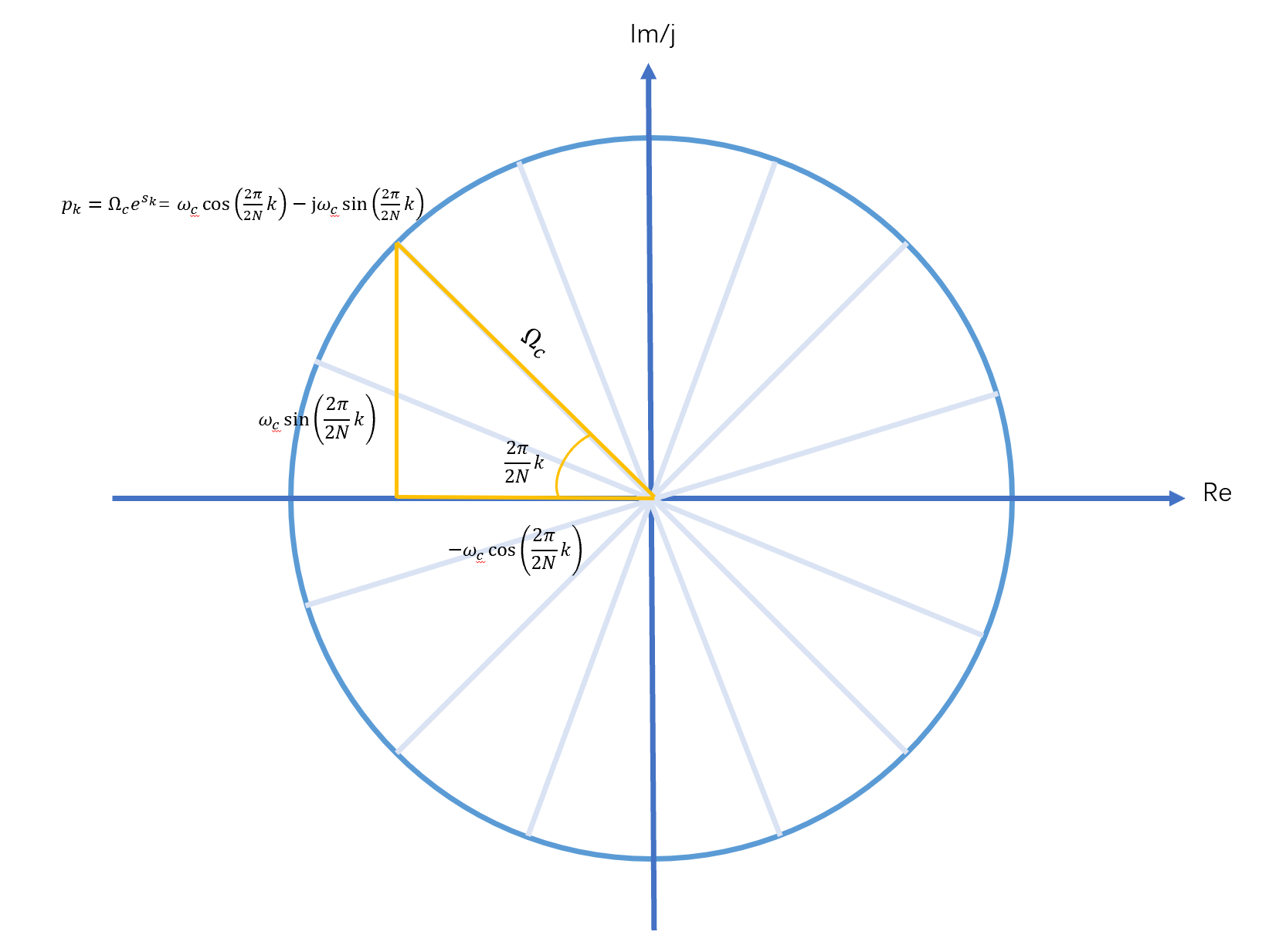
可以求得：
\[s_k=Ω_ccos(\frac{π}{N}k)-jΩ_csin(\frac{π}{N}k)\]

巴特沃斯滤波器的幅频响应在s域上表示为：
\[H_a(s)=\frac{Ω_c^N}{\prod(s-p_k)}\]

巴特沃斯滤波器设计

如果设计要求为指定的通带和止带截止频率，以及通带和止带的波纹：
根据\(R_p=-10lg|H_a(jΩ_p)|\)，\(A_s=-10-10lg|H_a(jΩ_s)|\)，有：
\[R_p=-10lg\frac{1}{1+(\frac{Ω_p}{Ω_c})^{2N}}\] \[A_s=-10lg\frac{1}{1+(\frac{Ω_s}{Ω_c})^{2N}}\] 两式相比可以得到：
\[N=\frac{lg[\frac{10^{R_p/10}-1}{10^{A_s/10}-1}]}{2lg(\frac{\omega_p}{\omega_s})}\] 向上取整。
根据\(R_p\)、\(A_s\)的表达式可以得到两个截止频率，截止频率\(Ω_c\)应当为这两式得出结果区间内的某个值：
\[Ω_c=(\frac{Ω_p}{\sqrt[2N]{10^{R_p/10}-1}},\frac{Ω_s}{\sqrt[2N]{10^{A_s/10}-1}})\]

切比雪夫滤波器

根据通带或止带存在波纹将切比雪夫滤波器分为两类：

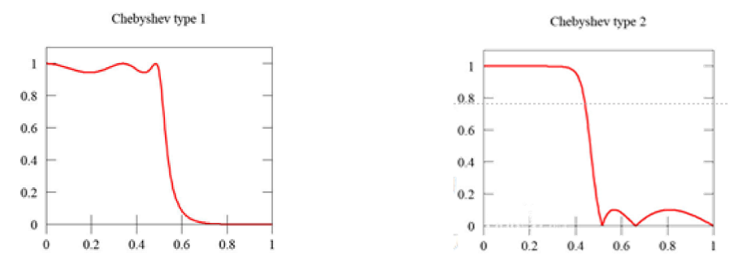
I型切比雪夫滤波器

I型切比雪夫滤波器的通带存在波纹，其频率响应为：
\[\lvert H_a(jΩ)\lvert^2=\frac{1}{1+ϵ^2T_N^2(\frac{Ω}{Ω_c})}\] \(T_N(x)\)为N阶切比雪夫多项式：
\[T_N(x)=\begin{cases} cos(Narccos(x)),0≤x≤1\\ cosh(Narccosh(x)),1≤x≤∞ \end{cases}\] > \(cosh(x)=\frac{e^x+e^{-x}}{2}\)

切比雪夫I型滤波器的s域分析

根据对s的定义：
\[H_a(s)H_a(-s)=\frac{1}{1+ϵ^2T^2_N(\frac{s}{jΩ_c})}\] 极点可以表示为：\(p_k=σ_k+jΩ_k\)
\[Ω_k=(bΩ_c)sin[\frac{π}{2}+\frac{(2k+1)π}{2N}]\] \[σ_k=(aΩ_c)cos[\frac{π}{2}+\frac{(2k+1)π}{2N}]\] \(a=\frac{1}{2}(\sqrt[n]{α}-\sqrt[n]\frac{1}{α})\)，\(b=\frac{1}{2}(\sqrt[n]{α}+\sqrt[n]\frac{1}{α})\)，\(α=\frac{1}{ϵ}+\sqrt{1+\frac{1}{ϵ^2}}\).

即在幅频响应中令\(Ω=\frac{s}{j}\)，带入后得到\(\lvert H_a(jΩ)\lvert^2=\frac{1}{1+ϵ^2T_N^2(\frac{s}{jΩ_c})}\)，令下方为0后得到的\(1+ϵ^2T_N^2(\frac{s}{jΩ_c})=0\)的方程解。

切比雪夫I型滤波器设计

根据\(R_p\)的定义，有\(Ω_c=Ω_p\)时， \[ϵ=\sqrt{10^{0.1R_p}-1}\] 滤波器的阶数为：
\[N=\frac{lg[g+\sqrt{g^2-1}]}{lg[\frac{Ω_s}{Ω_c}+\sqrt{(\frac{Ω_s}{Ω_c})^2-1}]}\] 其中：\(g=\sqrt{\frac{A^2-1}{ϵ^2}}\)

切比雪夫II型滤波器

切比雪夫II型滤波器在止带上有波纹，其系统幅频响应为：
\[|H_a(jΩ)|^2=\frac{1}{1+\left[ϵ^2T_N^2(\frac{Ω}{Ω_c})\right]^{-1}}\] 其余设计思路与切比雪夫I型滤波器相同。

模拟/数字滤波器转换

脉冲响应不变法

脉冲响应不变法的基本思路是在模拟滤波器的时域表达上等距采样，生成数字滤波器的序列。在脉冲响应不变法中，数字角频率和模拟角频率之间的关系是线性的：\(Ω=\frac{ω}{T}\)
\[h[n]=Th_c(nT)\] 如果模拟滤波器\(h_c\)的频率响应：
\[H_c(s)=∑_{k=1}^N\frac{A_k}{s-s_k}\] 在时域上：
\[h_c(t)=∑_{k=1}^NA_ke^{s_kt},t≥0\] 对其采样：
\[\begin{aligned}h[n]=&Th_c(nT)\\ =&\sum_{k=1}^NTA_ke^{s_knT}u[n]\\ =&\sum_{k=1}^NTA_k(e^{s_kT})^nu[n] \end{aligned}\] 对其做Z变换，得到对应的数字滤波器的频率响应：
\[H(z)=∑_{k=1}^N\frac{TA_k}{1-e^{s_kT}z^{-1}}\]

脉冲响应不变是一种一对多的映射：

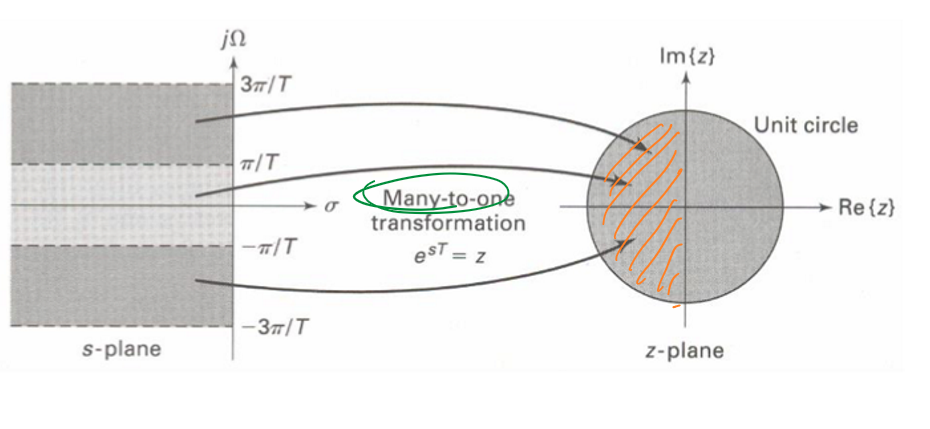
在采样的过程中，由于一对多的映射关系，采样信号会在频谱上发生混叠。

脉冲响应不变法的流程：
1. 根据设计要求的通带截止频率和止带截止频率将数字角频率还原为模拟角频率：\(Ω_p=\frac{ω_p}{T},Ω_s=\frac{ω_s}{T}\)。
2. 设计出对应的模拟滤波器。
3. 求出模拟滤波器的频率响应：\(H_c(s)=∑_{k=1}^N\frac{A_k}{s-s_k}\)。 4. 根据映射律：\(H(z)=∑\frac{A_k}{1-e^{s_kT}z^{-1}}\)，得到数字滤波器的频率响应。

双线性法

双线性法的映射律为：
\[s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\] 因此:
\[H(z)=H_a(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}})\]

这是一种一对一的映射律，因此不会发生混叠。

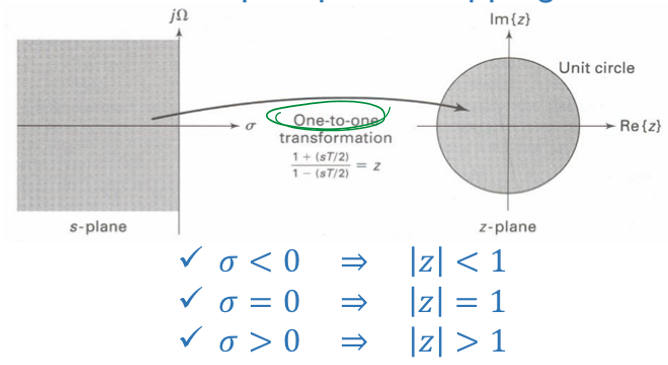
在这种映射律下，其数字角频率和模拟角频率之间的关系是非线性的： \[Ω=\frac{2}{T}tan\frac{ω}{2}\] 其频率响应表示为：
\[|H(e^{jω})|^2=\frac{1}{1+(\frac{tan(ω/2)}{tan(ω_c/2)})^N}\]

其他类型的IIR滤波器设计*

在模拟域中，滤波器类型的转换是线性的，但是在经过模数转换后，数字滤波器的类型转换是非线性的。
简单来说，IIR滤波器的类型转换通过映射律将低通滤波器频率响应的\(z^{-1}\)重新映射，进而得到其他类型的IIR滤波器的频率响应。
\[z^{-1}=G(z^{-1})\] \[H(z)=H_{LP}(z)|_{z^{-1}=G(z^{-1})}\] 并且映射律需要满足：\(|z^{-1}|=|G(z^{-1})|=1\)。

常见的映射律如下表所示：