电子系统-知识点总结
本文最后更新于 2025年6月4日 晚上
电子系统-知识点总结
晶体管电路部分
晶体管的直流分析
晶体管的直流分析普遍从\(i_b\)入手,利用三极电流之间的关系:\(i_c=βi_b=αi_e\),\(i_c≈i_e\)来求得整个电路各部分的值。
负载线
直流负载线是用来探究\(V_{CE}\)和\(I_C\)关系的直线:
\[V_{CE}=V_{CC}-I_CR_C\] \[I_C=-\frac{1}{R_C}V_{CE}+\frac{V_{CC}}{R_C}\] 知道\(I_S=\frac{V_{CC}}{R_C}\),即负载线的截距;和\(V_{CE}|_{max}=V_{CC}\),即直线与x轴的交点,就能确定晶体管电路的负载线。
晶体管的交流分析
由于电路中耦合电容的存在,因此交流分析和直流分析可以分别对同一个晶体管电路使用。基本步骤是:
- 只看直流,确定电路中的\(I_E\)、\(I_C\)、\(I_B\)。
- 将所有的直流电压源全部视为接地,直流电流源/电流镜电路全部视为短路,并根据发射极是否有额外的电阻画出电路的小信号模型。
发射极有额外的电阻\(R_e\):T模型
没有额外的电阻:π模型
两个晶体管发射极相连:T模型 - 根据直流分析中的\(I_E\)、\(I_C\)、\(I_B\),确定小信号模型中的\(r_e\)、\(r_π\)、\(g_m\)和\(R_0\)(厄利效应的等效电阻)。
- 一般而言,从基极开始分析,求出\(i_b\)后利用\(i_c=βi_b\)转到集电极分析。得到输出电压。
输入阻抗和输出阻抗
晶体管电路的输入阻抗和输出阻抗都是指的晶体管本身的阻抗,分析时应当去掉电路中的全部负载(如输出端电阻\(R_L\)、输入端电阻\(R_{sig}\))。
其次,在T模型中分析输入阻抗时,应当把发射极上的全部电阻通过等效\((β+1)(r_e+R_e)\)转到基极。
输入阻抗和输出阻抗的基本判断方法是当\(v_{in}=0\)时,从晶体管的输入端口和输出端口看到的电阻。
基本的两个双晶体管电路
电流镜
电流镜的分析从晶体管的集电极入手,将基极电流用\(I_B=\frac{I_C}{β}\)表达后求出\(I_{REF}\)与\(I_C\)的关系。
集电极电压/基极电压需要利用\(V_C=V_B=V_{BE}+V_E\)求解,再求出\(I_C\)。
电流镜的输出电流与输入电流的关系为:
\[I_{o}=area × I_{REF}\] \(area\)是pn结的面积比。
差分对
对于差分放大电路,求其差分增益,其分析思路有两个:
- \(A_d=\frac{v_{od}}{v_{id}}\frac{v_{id}}{v_{sig_d}}\)
这是一种“两边一起看”的分析思路,\(\frac{v_{od}}{v_{id}}\)可以通过晶体管内部输出端电阻和输入端电阻之比\(\frac{R_{od}}{R_{id}}\)得到。\(\frac{v_{id}}{v_{sig_d}}\)通过分析基极的分压情况得到。
- 对每个晶体管分开来看
通过对基极的分析得到\(i_b\),利用\(i_c=βi_b\)的关系转入集电极分析,用\(v_{sig1}\)表达\(v_{o1}\)。最后用\(v_{od}=v_{o1}-v_{o2}\)求得含有\(v_{sigd}\)的表达式,移动表达式即可得到差分增益。
其他交流分析中用到的重要概念
- 差分输入
交流分析下\(i_C=I_Se^{\frac{V_{BE}}{V_T}}\)。
在差分放大器电路中可以利用\(V_{BE}=V_B-V_E\)分别带入两晶体管电路,两式相比可以求得差分输入。
- 晶体管的开环增益
开环增益指的晶体管输出端口和输入端口的电压之比:\(A_{ol}=\frac{v_{o}}{v_{i}}\)。
- 晶体管电路的差分增益
差分增益指差分电路中差分电路的输出信号之差与输入信号之差的比:\(A_d=\frac{v_{od}}{v_{sigd}}\)。
- 共模增益和共模抑制比
共模增益指的当输入信号相同,但是两个\(R_C\)不同引起输出信号不同时的差分增益。 定义共模增益为差分电压和输入电压之比:
\[A_{cm}=\frac{v_{od}}{v_{icm}}=-\frac{αΔR_C}{r_e+2R_{EE}}\] 定义共模抑制比为其差分增益与共模增益之比:
\[CMRR=\frac{A_d}{A_{cm}}\]
放大电路的频率响应
由于完整的放大电路中存在耦合电容,当输入的电压信号频率较低时,这些电容的容抗无法在电路分析中忽略,因此放大电路的增益在输入信号为低频信号时有所损失。
下图表示了晶体管放大电路的频率响应特性曲线:
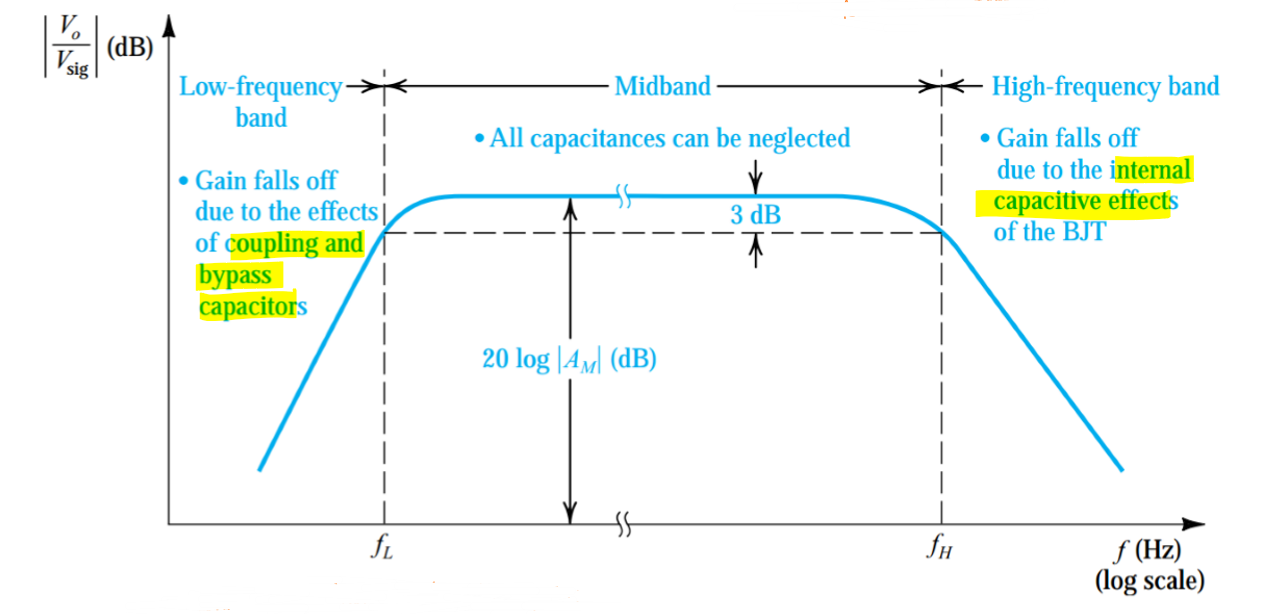
集成放大器中(比如第10讲的多级放大电路)不存在电容,因此其性能不会受到输入信号中低频分量的影响。但是高频时晶体管内部的类似电容的表现特性也会使得其性能在高频时存在损失。
集成放大器电路部分
运算放大器的参数特性
增益带宽积(GBP)
频率响应图中某时刻下的增益和带宽的乘积。
\[GBP=Gain × Bandwidth\]
共模抑制比
运算放大器的共模增益将放大直流噪声。共模抑制比(Common Mode Rejection Ratio,CMRR),定义为差模增益与共模增益的比值:
\[CMRR=\frac{A_d}{A_{cm}}\] \[CMRR(dB)=20lg\frac{A_d}{A_{cm}}\]
压摆率
理想的运算放大器在输入电压接入运算放大器的同时就会立即有稳定的输出电压,然而实际的运算放大器由于内部电容充电过程的存在,需要经过一小段时间才能达到稳定输出电压\(V_o\),达到稳定输出电压的最大速率称为压摆率或电压转换速率(Slew Rate)。
\[S.R.=\frac{dV_o}{dt}|_{max}\]
输入信号为频率\(f\)的正弦交流电时: \[S.R.=2πAf\] 可以得到运算放大器所支持的某峰值下的最大信号频率(全功率带宽)为:
\[f_{max}=\frac{S.R.}{2πA}\]
泄露和补偿
在真实的放大器中,输入端\(V_+\)和\(V_-\)之间是有电流的,这个电流称为泄露电流,在反相放大器中这个电流会流向\(V_+\)的接地端。泄露电流的存在会造成假设\(V_+=V_-\)不成立,因此在运算放大器的内部需要添加一个补偿电容来对\(V_+\)和\(V_-\)的电压进行补偿。
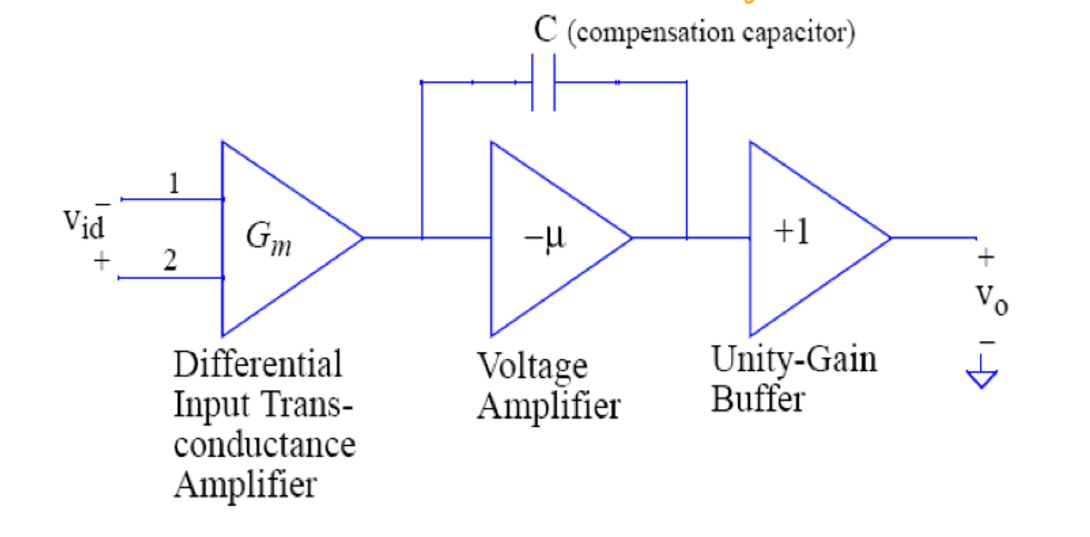
同时在接地端需要额外增加一个补偿电阻以减小泄露电流的影响。在集成化的仪用放大器中,有两个pin:offset用于额外连接一个变阻器,调节补偿电阻的大小。
反馈放大器电路
反馈放大器的类型
反相放大器
信号从反相输入端输入,其增益为:
\[\frac{V_{out}}{V_{sig}}=-\frac{R_f}{R_i}\]同相放大器
信号从同相输入端输入,其增益为:
\[\frac{V_{out}}{V_{sig}}=1+\frac{R_f}{R_i}\]
反馈放大器电路的分析原则:
- 有多个输入的情况下,将其他输入暂时视为接地,单独分析每一个输入对输出电压的影响。在分析每一个输入时:
- 需要关注放大器端口的输入电压。
- 利用理想放大器同相输入端口和反相输入端口电压相等,建立关于电流的方程。
- 需要关注放大器端口的输入电压。
- 利用叠加定理,求和求解即可。
反馈放大器的频率响应
反馈放大器的频率响应如图所示:
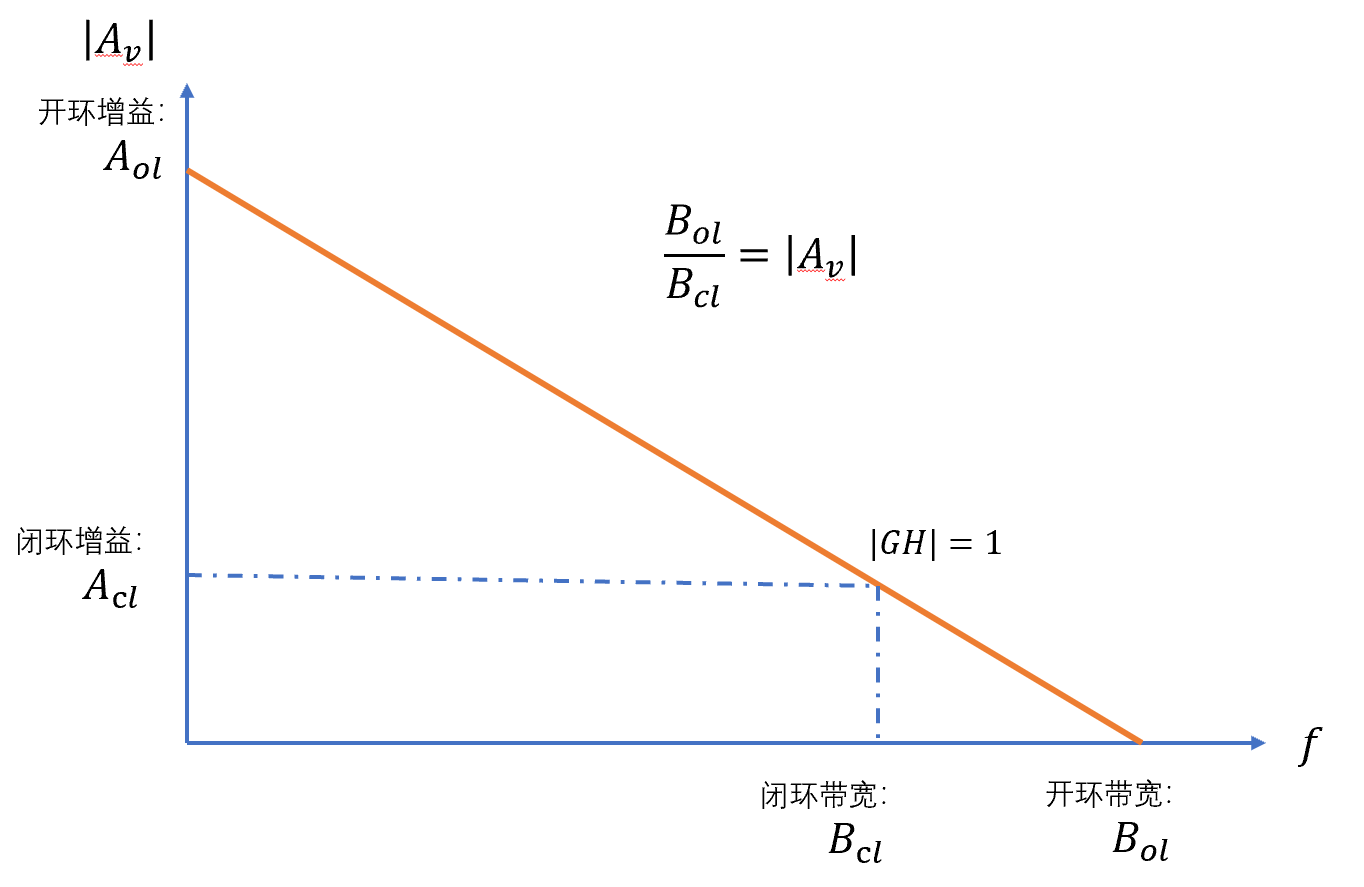
反馈放大器的开环带宽和闭环带宽之间存在着如下关系:
\[B_{cl}=\frac{B_{ol}}{A_v}\] 其中\(A_v\)是运算放大器的电压增益。
反馈电路的类型
最简单的判断电路属于哪种反馈类型的方式为看电路中反馈部分两端是否存在额外的接地电阻,如下图所示:
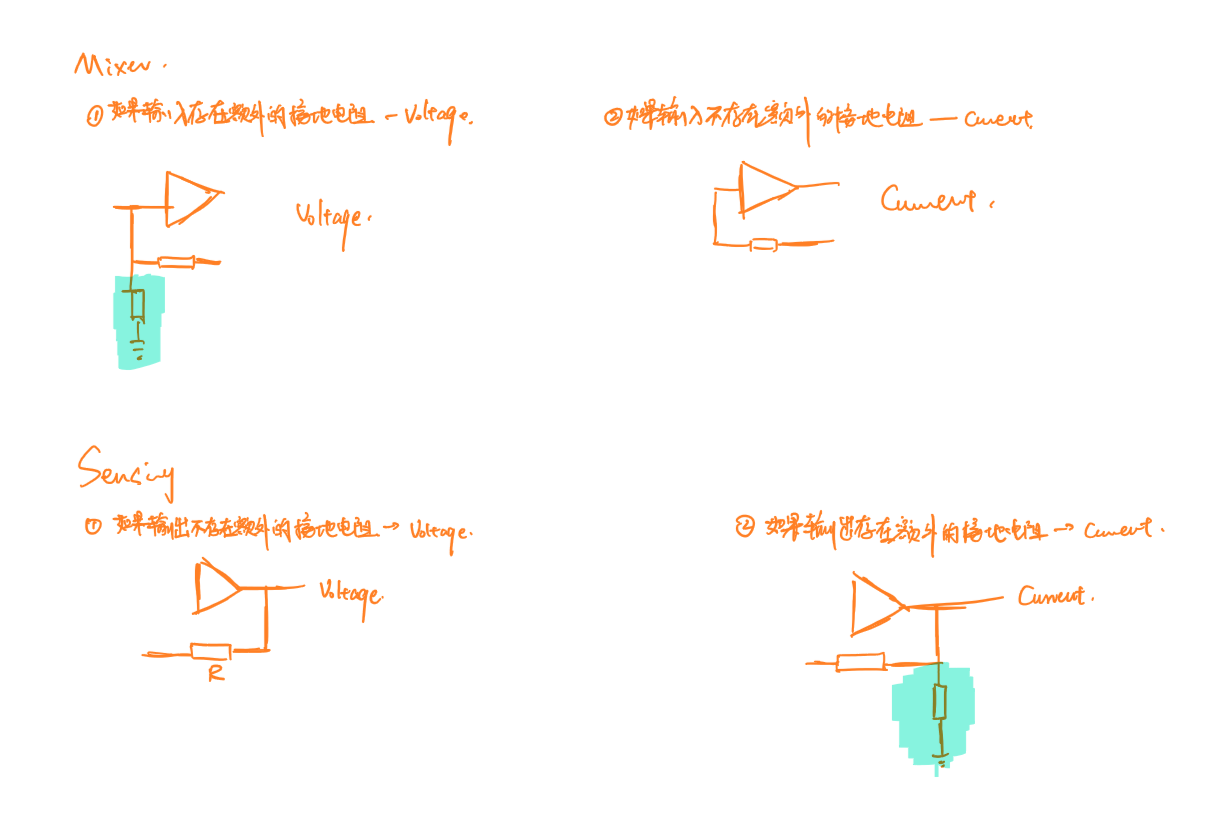
注意反馈电路的类型名称是先写出输出端(sensing)的反馈类型,再写出输入端(mixer)的反馈类型。
滤波器电路
基本的滤波器有高通,低通两种类型,其截止频率都为:
\[f_c=\frac{1}{2πRC}\] 对于多级高通/低通滤波器,其截止频率为:
\[f_c=\frac{1}{2π\sqrt[n]{∏_iR_iC_i}}\]
| 名称 | 电路图 | 被测目标 | 截止频率 | 下降/上升斜率 | 达到截止频率时的相移 |
|---|---|---|---|---|---|
| 一阶低通滤波器 | 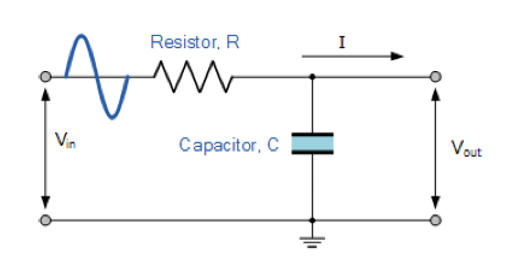 |
C | \(\frac{1}{2πRC}\) | -20dB | -45° |
| 一阶高通滤波器 | 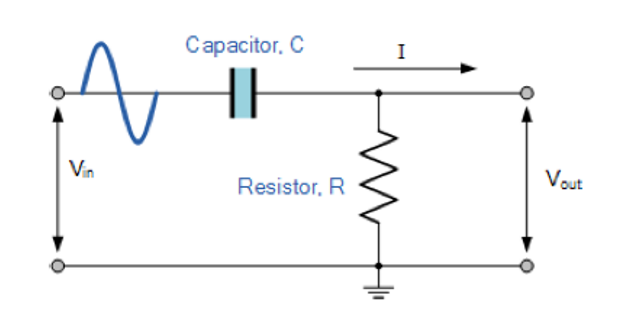 |
R | \(\frac{1}{2πRC}\) | 20dB | 45° |
| 二阶低通滤波器 | 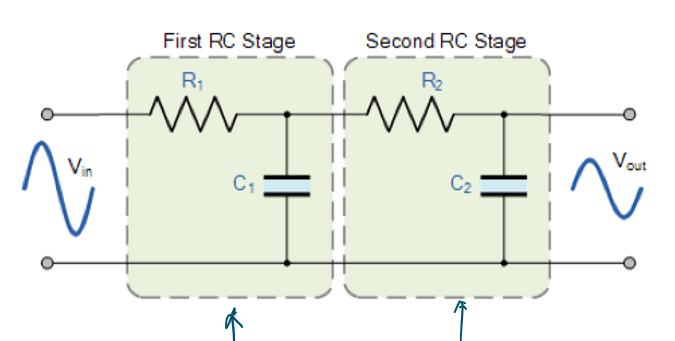 |
C | \(\frac{1}{2π√(R_1R_2C_1C_2)}\) | -40dB | -90° |
| 二阶高通滤波器 | 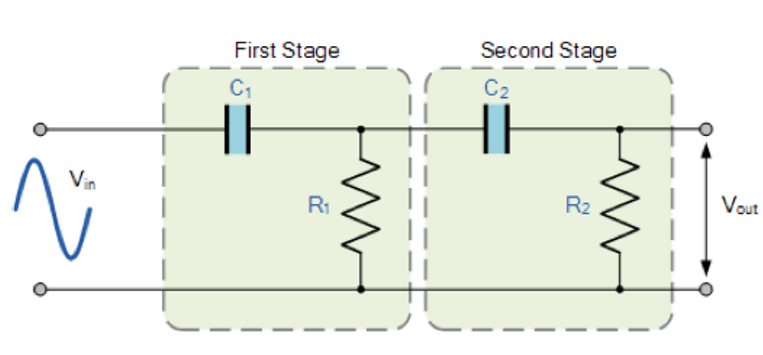 |
R | \(\frac{1}{2π√(R_1R_2C_1C_2)}\) | 40dB | 90° |
| 带通滤波器 | 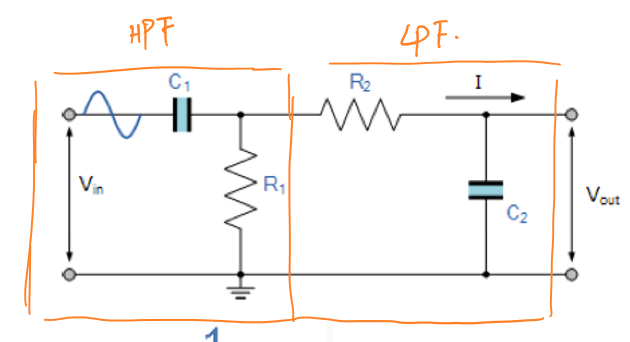 |
R、C | \(f_r=\frac{1}{2π√(R_1R_2C_1C_2)}\) \(f_H=\frac{1}{2πR_1C_1}\) \(f_L=\frac{1}{2πR_2C_2}\) |
20dB -20dB |
0° 90° -90° |
分析滤波器电路的方法:
- 模拟电路中输入信号为高频输入信号或者低频输入信号时的情况,通过电容“隔直流,通交流”的特性,分析电路中每个电容的开闭对输出的影响,以此来判断是高通滤波器还是低通滤波器。
- 对每个电容单独分析,判断其截止频率。
- 如果为有源滤波器,还需要对放大电路分析其增益。
放大电路部分和滤波器电路部分相互隔离,其中的电阻阻值互不影响。
滤波器的频率响应
滤波器的频率响应图中应当关注:
- 最大增益\(A_m\)
- -3dB处,对应截止频率。
需要注意的是带通滤波器的频率响应图中,较低的截止频率对应的是高通滤波器部分的截止频率,较高的截止频率对应的是低通滤波器部分的截止频率。
振荡器电路
满足稳定振荡的两个条件:
- \(|GH|=1\).
- 相移为0°
有两种策略来实现稳定的振荡器:文氏电桥振荡电路和相移振荡器。
文氏电桥振荡器
文氏电桥电路图如下,这是一个带通滤波器:
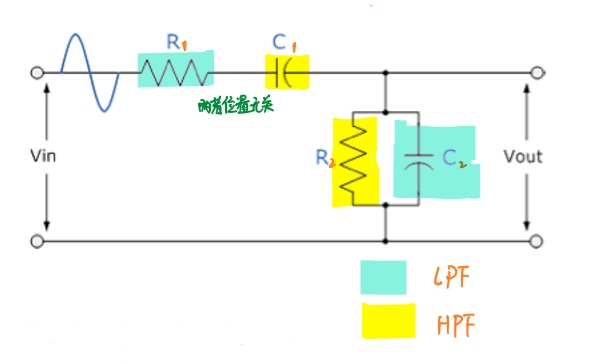
其在输入信号为中心响应频率时可以满足相移为0°的条件: \[f_r=\frac{1}{2π\sqrt{R_1R_2C_1C_2}}=\frac{1}{2πRC},R_1=R_2=R,C_1=C_2=C\]
电桥电路输出到放大器的同相输入端,以确保相移为0°,产生稳定的振荡。
同相输入端的电阻需要满足:
\[1+\frac{R_f}{R_{in}}>3\] 才能够确保\(|GH|=1\)。
同时放大器的反相输入端可视为一个反相放大器,以负反馈确保电路输出稳定。
相移振荡器
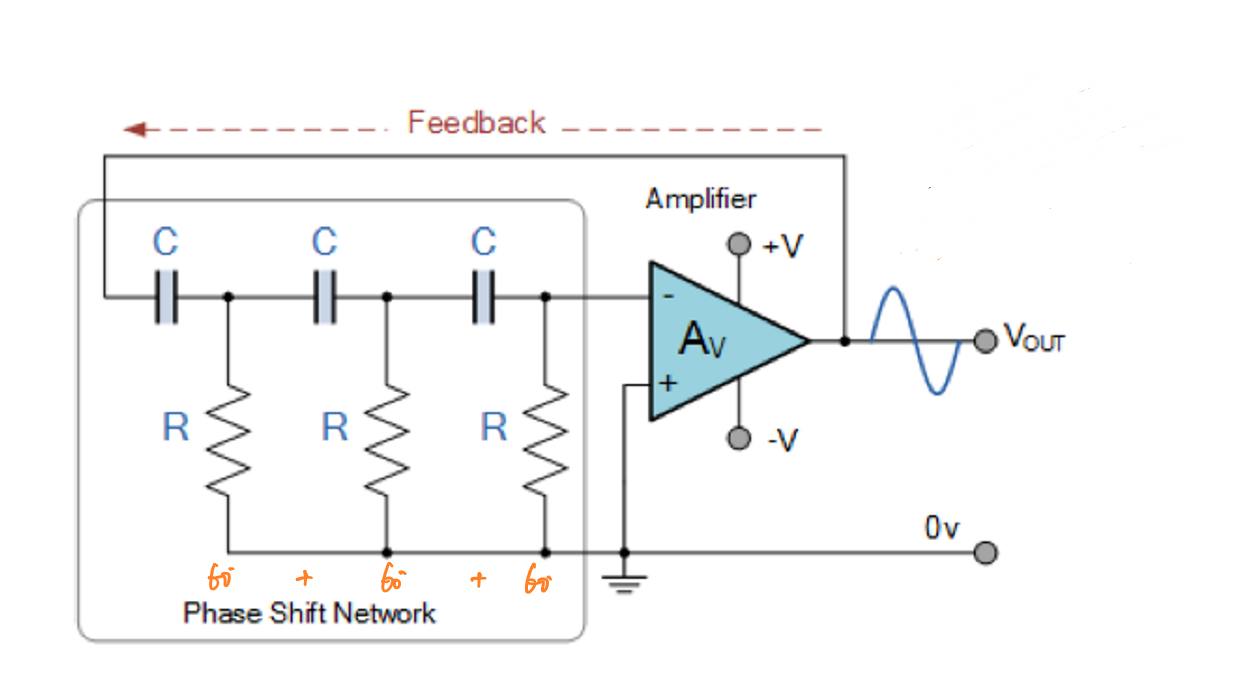
相移器通过高通滤波器的并联实现,根据高通滤波器的频率响应关系和相移公式可知,每个相移器的相移为:
\[Δφ=arctan\frac{X_c}{R}\] 通过调整电路中RC的值即可使其在输入信号频率\(f_r\)固定的情况下产生特定的相移。
当高通滤波器并联时,要使相移平均到高通滤波器,有如下公式:
\[f_r=\frac{1}{2πRC\sqrt{2N}}\] 其中\(N\)代表高通滤波器的个数,它与相移之间满足如下关系: \[Δφ=\frac{180°}{N}\] 需要注意的是,\(N\)的值越大,所需要的器件越多,同时由于每个高通滤波器在\(f_r\)处的增益都小于0,对所连接的运算放大器电压增益的要求也更高:运算放大器的电压增益需要大于所有高通滤波器在\(f_r\)的增益之和,该电路才能正常工作。通常认为\(A_v≥29\)。
555定时器
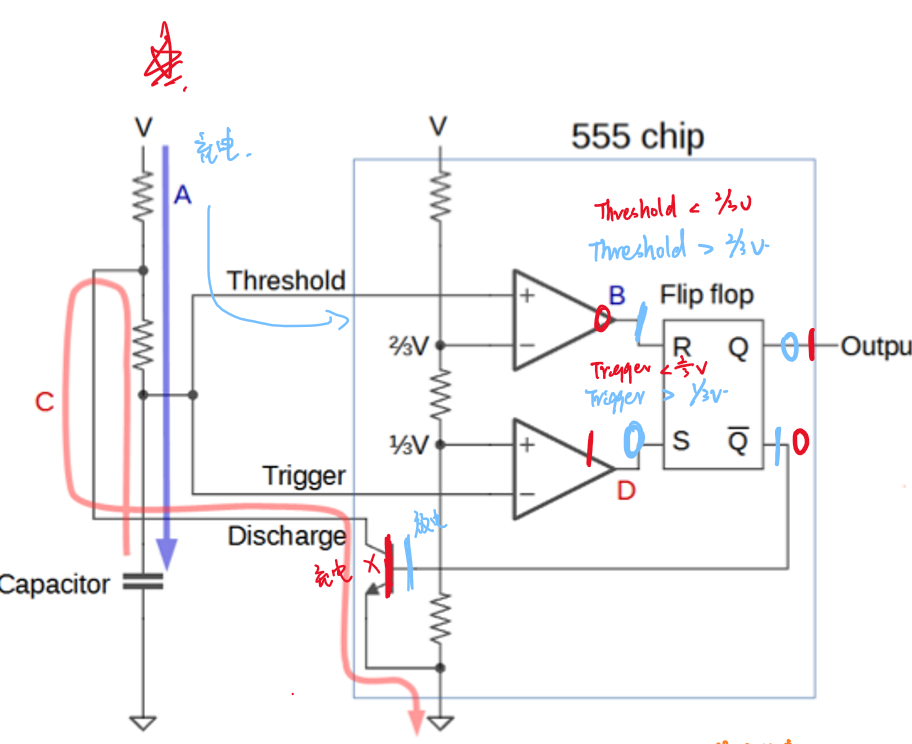
55定时器是一种利用电容器充放电性质的电路元件,它可以通过直流电压输出稳定的方波。其元件内部结构如图所示:
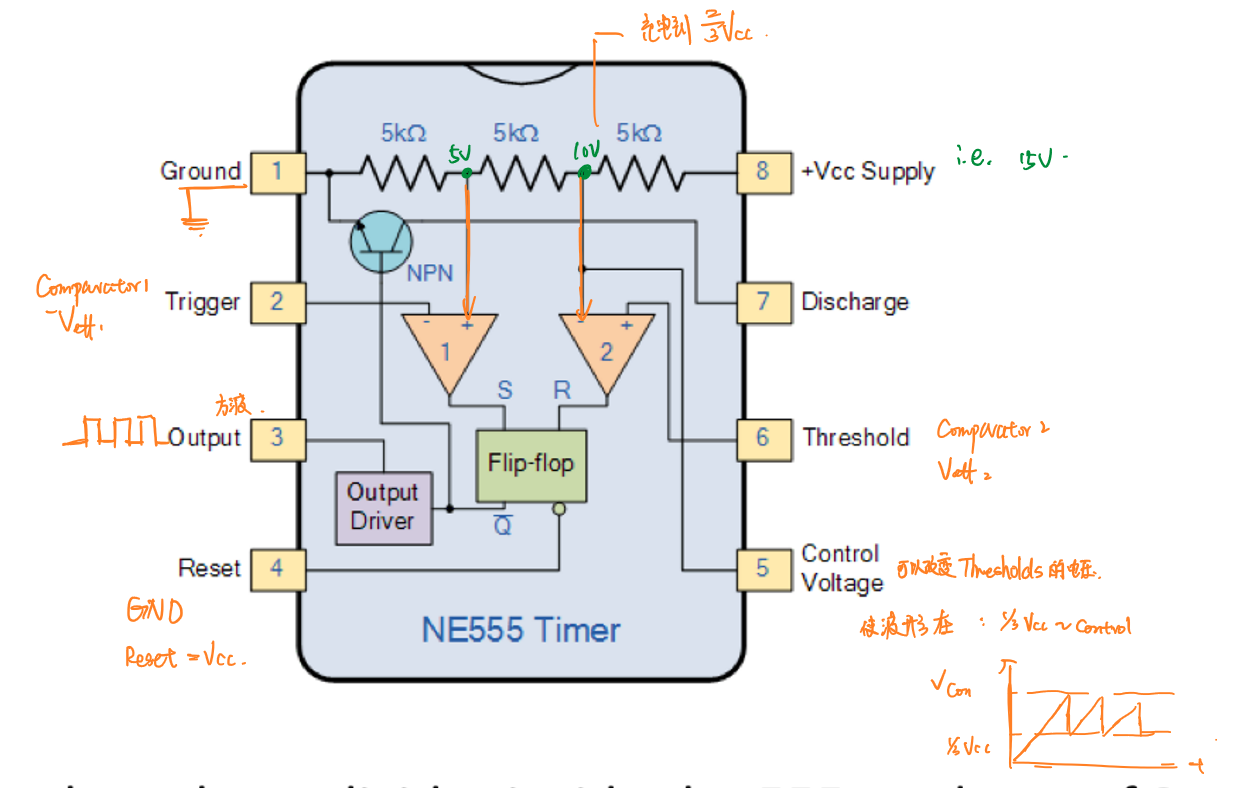
其中的NPN晶体管作用类似于开关。上方三个\(5kΩ\)的分压器将输入电压\(V_{cc}\)分割成\(\frac{2}{3}V_{cc}\)和\(\frac{1}{3}V_{cc}\)并分别送入比较器2、1。其中比较器2将\(\frac{2}{3}V_{cc}\)与外接电压Threshold进行比较,比较器1将\(\frac{1}{3}V_{cc}\)与外接电压Trigger进行比较,以控制SR触发器的输入。
同时,555定时器还支持使用ControlVoltage替代\(\frac{2}{3}V_{cc}\)作为比较电压。SR触发器的输出为Ouput和Reset。
555定时器有三种工作状态(电路连接方式):非稳态、单稳态和多稳态,这三种连接分别可以产生三种不同的方波波形。
非稳态模式
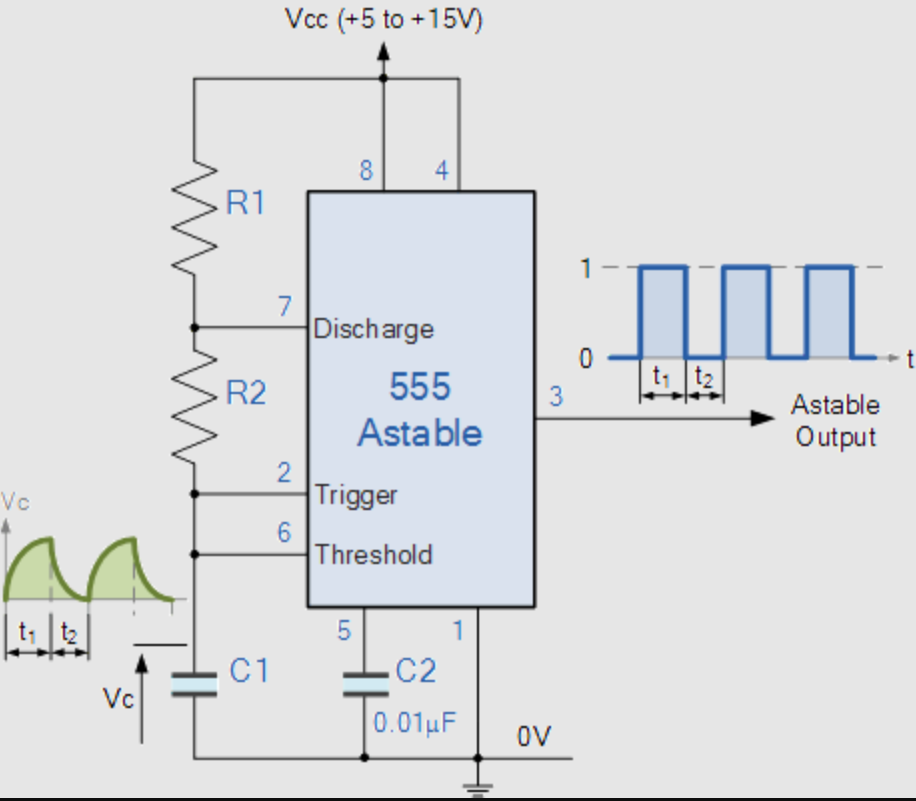
非稳态模式(Astable)下555定时器的连接图如下图所示:
如图,VCC分别作为内部和外部电路的电压源,外部电路是一个基本的RC电路。而外部电路的输出端与Threshold和Trigger连接,从而起到自我触发的效果。
开始时电容器充电,当\(Threshold>\frac{2}{3}V_{cc}\)时,SR触发器输入逻辑为:\(R=1,S=0\),输出为低电平,同时由于\(\overline{Q}=1\),NPN晶体管被导通,电容器开始放电。
当\(Threshold<\frac{2}{3}V_{cc}\)时,SR触发器输入逻辑为:\(R=0,S=1\),输出为高电平,同时由于\(\overline{Q}=0\),NPN晶体管关断,电容器充电。
此后,由于Threshold/Trigger电压的变化,电容器会不断地进行充放电,从而在输出端产生稳定的高低电平方波,而电容器处产生稳定的锯齿波三角波,且周期占空比与输出的方波信号完全相同:
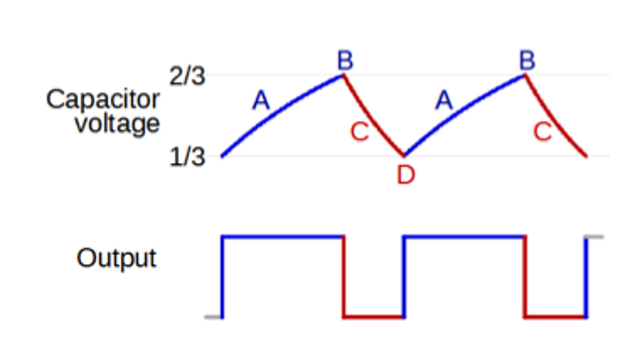
可以发现锯齿波/三角波的上下限为\(\frac{2}{3}V_{CC}\)(或者ControlVoltage)和\(\frac{1}{3}V_{CC}\)。
在电路连接时往往还会增加另一个电容\(C_2\)以提高电路的稳定性。
有关计算
在电容器充电过程,电流实际上流过了外部的两个电阻\(R_1、R_2\),因此充电过程的时间常数:\(τ_1=(R_1+R_2)C_1\)。
放电过程中电流只流过了\(R_2\),因此放电过程的时间常数:\(τ_2=R_2C_1\)。
根据数学推导得到充电时间:
\[t_{char}=ln2(R_1+R_2)C_1\] 放电时间:
\[t_{Discr}=ln2R_2C_1\] 周期:
\[T=t_{char}+t_{Discr}=ln2(R_1+2R_2)C_1\] 振荡频率:
\[f_r=\frac{1}{T}=\frac{1.44}{(R_1+2R_2)C_1}\] 定义输出波形一周期内的高电平出现时间占整个周期时间的比例为占空比,有:
\[Duty Cyecle=\frac{R_1+R_2}{R_1+2R_2}× 100\%\] 因此,非稳态的555定时器输出的方波可以通过改变\(R_1\)和\(R_2\)的值改变占空比。
可以发现这种基本的非稳态555振荡器配置的问题在于占空比,因为电阻\(R_2\)的存在使得占空比永远大于50%。
换句话说,该电路不能使输出“ON”时间短于“OFF”时间,因为\((R_1 + R_2)C\) 总是大于\(R_1C\)的值。
> 当\(R_2\)远大于\(R_1\)时,\(Duty Cyecle=50\%\)。
\(V_{Control}\)对输出波形的影响:
充放电时间中的参数\(ln2\)实际上是由\(\frac{1}{3}V_{CC}\)和\(\frac{2}{3}V_{CC}\)进行决定的:
\[Const=ln\frac{V_{CC}-0.5V_{Control}}{V_{CC}-V_{Control}}\] 当\(V_{CC}=15V,V_{Control}=\frac{2}{3}V_{CC}\)时,\(Const=ln2\)。
如果Pin5:Control-Voltage接入直流电压,则\(V_{Control}≠\frac{2}{3}V_{CC}\)。
此时产生的三角波的上下限应该为:\(\frac{1}{3}V_{CC}-V_{Control}\)。
输出的方波周期发生变化,高电平和低电平的持续时间同比例增加或者减小,占空比仍然保持不变。