01. 控制系统的组成和模型表示
本文最后更新于 2025年6月4日 晚上
控制系统的组成和模型表示
控制系统概述及其结构
一个基本的系统由输入、输出和处理(Process)三部分构成。其中的处理是用于实现系统功能的装置(Device),比如某些函数、子系统、功能等。

控制系统是一种可以调整内部配置达到所需要的响应的系统。控制系统同时是为了使被控制对象达到预定的理想状态而实施的。控制系统使被控制对象趋于某种需要的稳定状态。下图反映了一个基本的反馈控制系统。
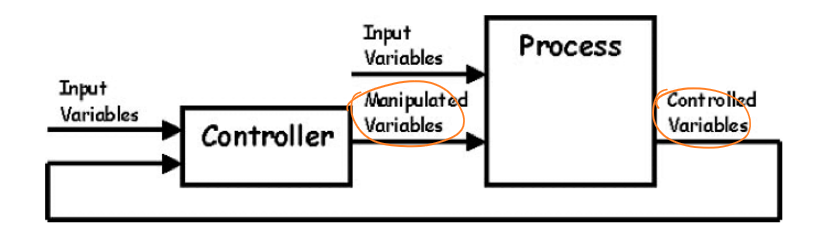
如上图所示,基本的反馈控制系统包括控制器(Controller)和处理(Process)两部分,通过对控制器和处理进行输入和可能含有的系统反馈来调整当前的系统输出。
在控制系统中有如下的输出变量:
- 受控变量(Controlled Variable):整个控制系统的输出变量,是一种可被测量和控制的状态或值。
- 操纵变量(Manipulated Variable):控制器的输出变量,并且该输出变量可以影响整个控制系统的输出,即受控变量。
此外,控制系统中还可能存在一些其他可能对系统产生不利影响的杂信号,称为干扰(Disturbance)。
在电子系统中,控制系统还包括其他两个组成部分:
- 传感器(Sensor):将物理参数转换为电子信号输出的转置,通常在转换过程中含有噪声。
- 驱动器(Actuator):将电子信号转换为物理输出的转置。
控制系统的分类
无反馈称为开环控制系统(open-loop control system),这种系统的输入直接供给控制器,并通过控制器对受控对象产生控制作用。其主要优点是结构简单、价格便宜、容易维修;缺点是精度低,容易受环境变化(例如电源波动、温度变化等)的干扰。

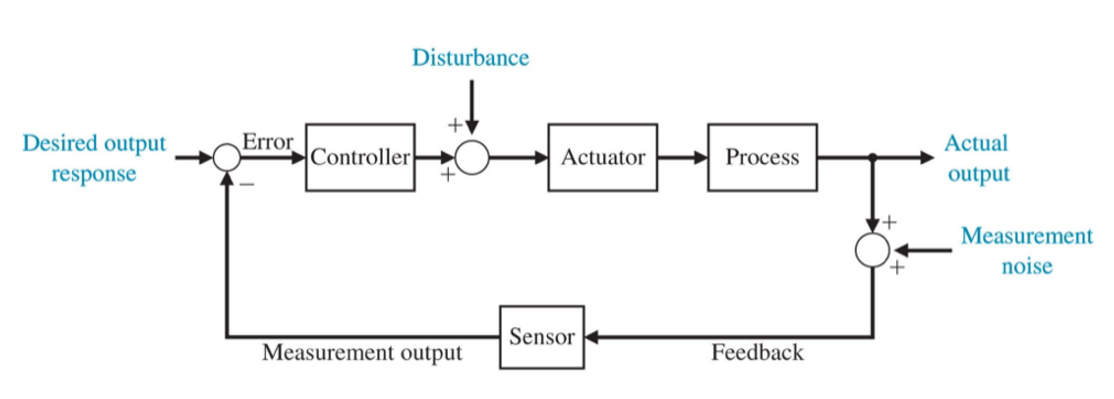
有反馈称为闭环控制系统(closed-loop control system),输入与反馈信号比较后的差值(即偏差信号)加给控制器,然后再调节受控对象的输出,从而形成闭环控制回路。所以,闭环系统又称为反馈控制系统,这种反馈称为负反馈。与开环系统相比,闭环系统具有突出的优点,包括精度高、动态性能好、抗干扰能力强等。它的缺点是结构比较复杂,价格比较贵,对维修人员要求较高。
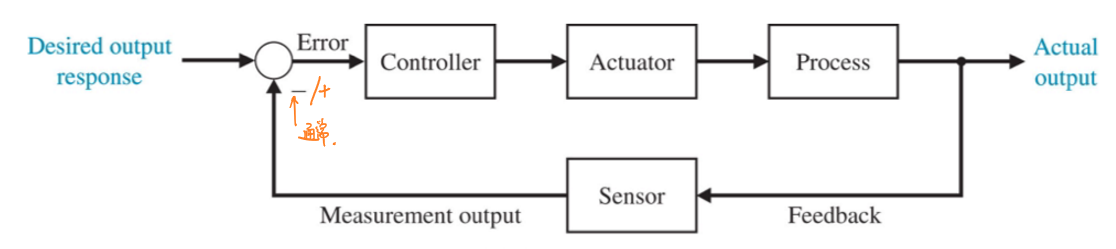
反馈控制可以存在多个,或者嵌套关系,如下图所示:
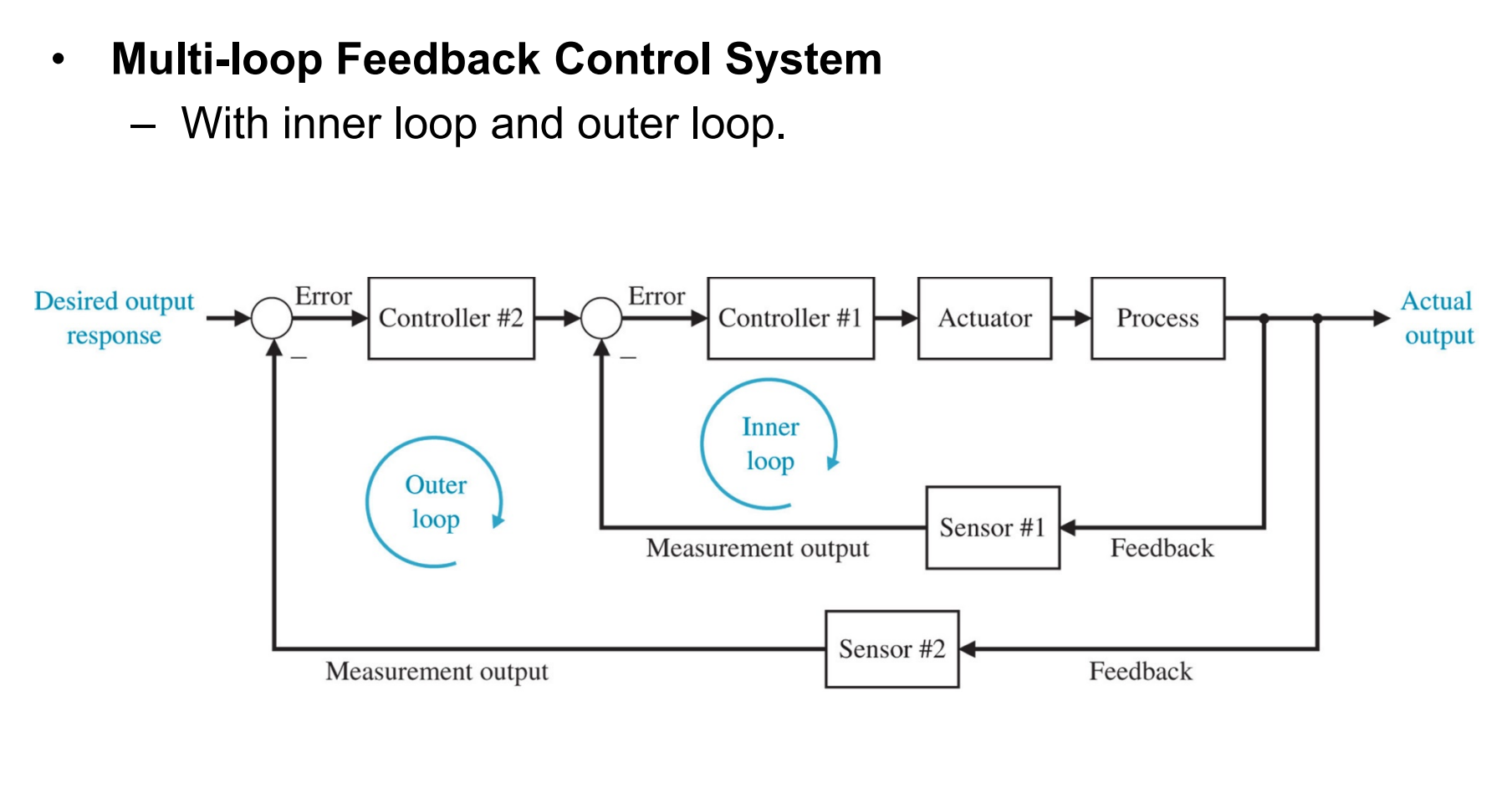
由于正反馈存在不稳定性,因此本课程的研究对象主要为负反馈系统。
反馈控制的目的在于:
- 让系统实现定式功能
- 减小系统的变化和干扰对系统的影响
- 让系统动态地根据需求而变化
- 让原本不稳定的系统持续地稳定
此外,系统还可以分为:
- 线性/非线性系统:如果输入和输出的关系为线性,则为线性系统,否则为非线性系统。
- 时变/时不变系统:如果系统输出与时间无关,则为时不变系统,否则为时变系统。
- 因果/非因果系统:如果系统输出仅与当前输入和之前的输出有关,与未来输入无关,则为因果系统,否则为非因果系统。
- 连续/离散系统:如果系统所有的变量都随时间连续变化,则为连续系统。如果系统存在一个或多个变量,其值仅在某些特定时刻已知,则为离散系统。
- 确知/随机系统: 如果系统随输入的响应是可重复可预测的,则为确知系统,否则为随机系统。
本课程主要讨论线性时不变系统(LIT system)。
系统模型:描述系统的方式
微分方程
系统可以描述为系统输入\(x(t)\)和系统输出\(y(t)\)之间的线性微分方程:
\[\frac{d^n}{dt^n}y+a_{n-1}\frac{d^{n-1}}{dt^{n-1}}y+...+a_1\frac{d}{dt}y+a_0y=b_m\frac{d^m}{dt^m}x+...+b_1\frac{d}{dt}x+b_0x\]
传输方程
在s域下,系统的微分方程表示为:
\[Y(s)[s^n+a_{n-1}s^{n-1}+...+a_1s+a_0]=X(s)[b_ms^m+b_{m-1}s^{m-1}+...+b_1s+b_0]\] 定义系统的转换方程为:
\[H(s)=\frac{Y(s)}{X(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+...+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_1s+a_0}\] 其中:\(n\)是系统的阶
定义系统的特征方程为:\(s^n+a_{n-1}s^{n-1}+...+a_1s+a_0=0\) 特征方程的根称为系统的极点(Pole),以×表示。
\(H(s)=0\)的根称为系统的零点(Zero),以○表示。
系统框图
标准反馈控制系统的系统框图
标准的反馈控制系统框图如下所示:
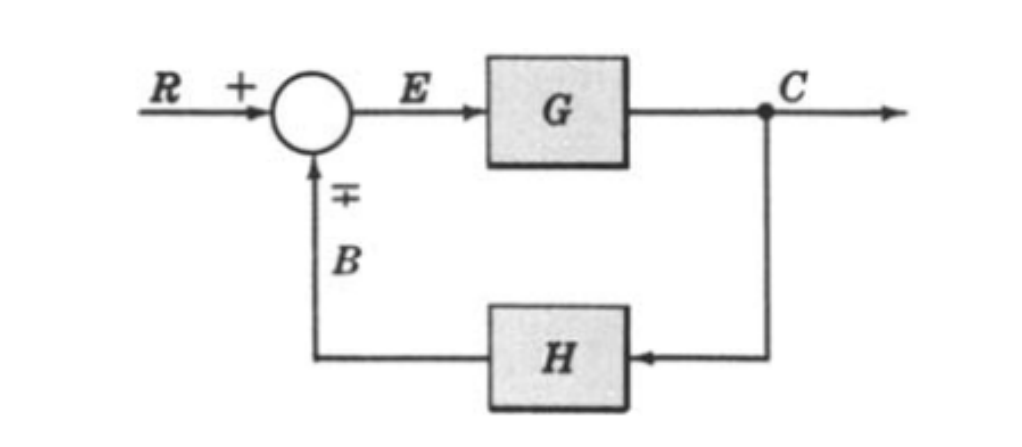
其中\(G(s)\)为前向传递函数,\(H(s)\)为反馈传递函数,\(E(s)\)为误差,是输入与输出的差值,有\(E(s)=R(s)-C(s)\)。
\(G(s)H(s)\)为系统的开环传递函数。
整个反馈系统的转换方程为:
\[\frac{C}{R}=\frac{G}{1± GH}\] 这也称为系统的控制比(Control ratio)。
系统的误差比为:
\[\frac{E}{R}=\frac{1}{1± GH}\]
系统框图化简
系统框图化简遵循如下的六个规则:
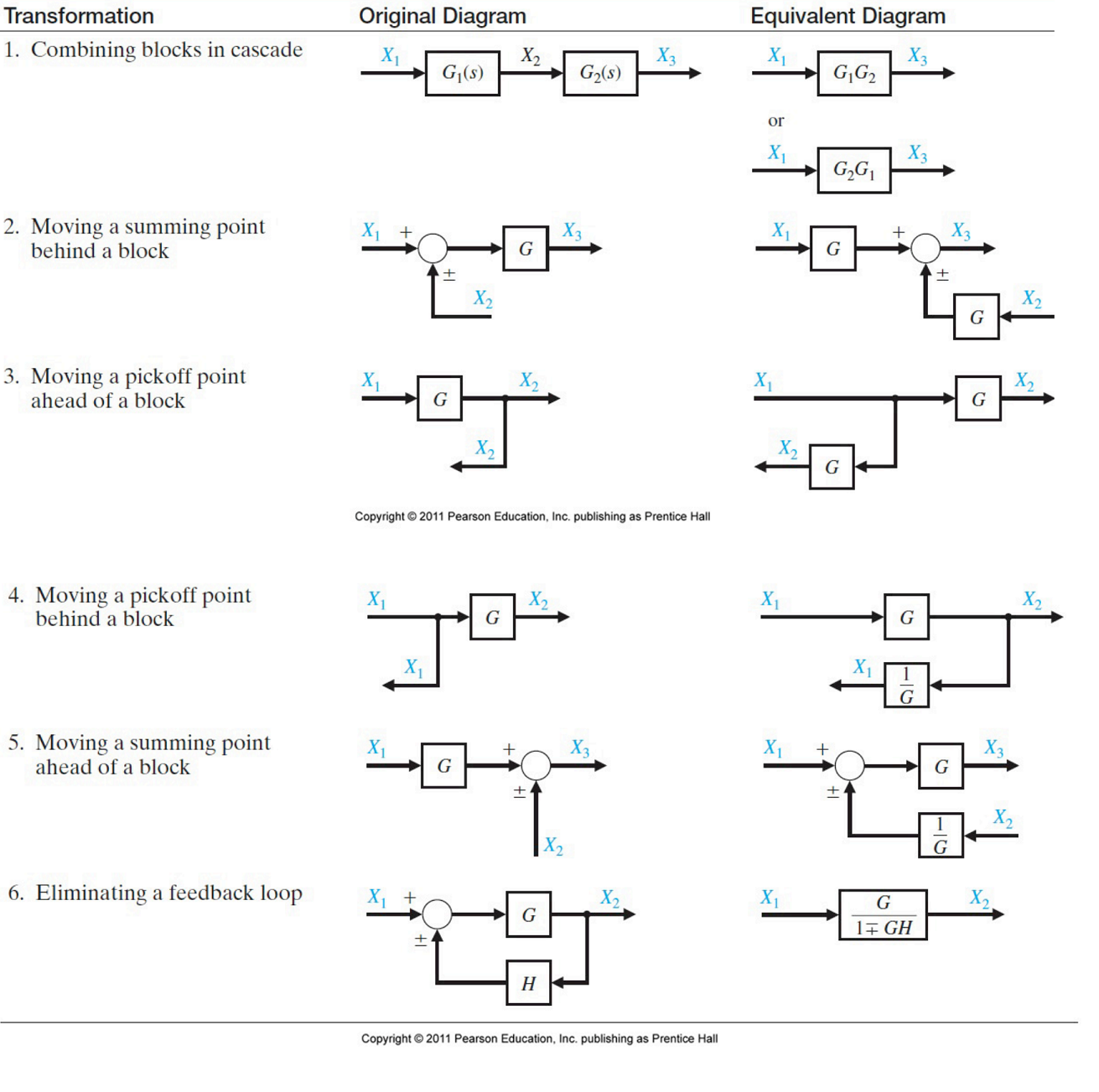
信号流图
信号流图的基本组成部分包括:
- 节点:表示求和
- 箭头:表示流动的方向
- 箭头上方的标注表示乘法器或者其他系统
一个基本的信号流单元如下图所示:

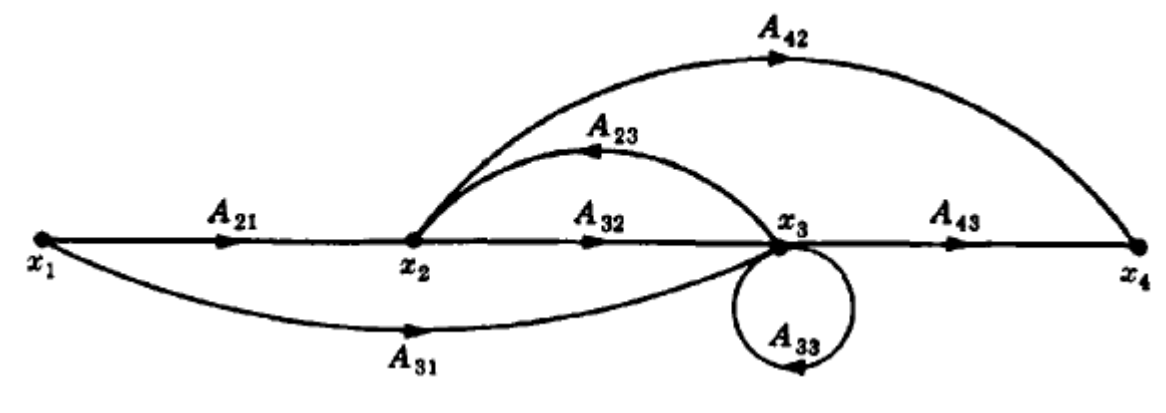
信号流图中可能会出现自循环(Self-loop),自循环中箭头的方向对信号流分析没有影响,一般规定为顺时针。
如下图的\(x_3=A_{31}x_1+A_{32}x_2+A_{33}x_3\)