02. 控制系统的瞬态和稳态响应分析

控制系统的瞬态和稳态响应分析

对于控制系统而言，其系统方程由两部分组成：系统在到达稳定状态前的响应——称为瞬态响应（\(c_{tr}(t)\)，Transient response）和系统在达到稳定状态后的响应——称为稳态响应（\(c_{ss}(t)\)，Steady-state response），整个系统响应\(c(t)\)表示为：
\[c(t)=c_{tr}(t)+c_{ss}(t)\] 定义系统的误差信号(error signal)为\(e(t)\)，是输入与输出的差值：
\[e(t)=r(t)-c(t)\] 如果系统在稳态条件下的输出与输入不等，其输入与输出的差值称为稳态误差（\(e_{ss}(t)\)，Steady-state error），它反映了系统的准确性：
\[e_{ss}(t)=r(t)-c_{ss}(t)\]

基本信号类型

由于基本信号类型已在课程“信号与系统”中详述，在此不做过多描述。
在控制系统分析中会用到的基本信号如下表所示：

信号类型	表达式（时域）	表达式（s域）	图示
单位冲击信号	\(δ(t)=1,t=0\)	\(δ(s)=1\)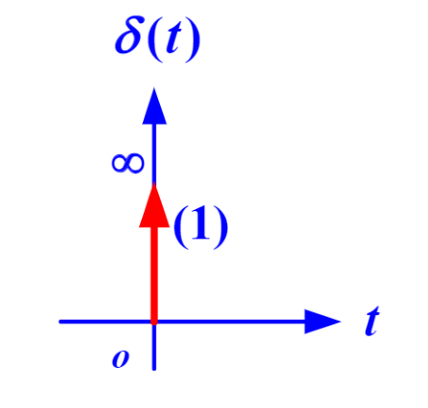
单位阶跃信号	\(u(t)=\begin{cases}1,t≥0 \\0,t>0 \end{cases}\)	\(u(s)=\frac{1}{s}\)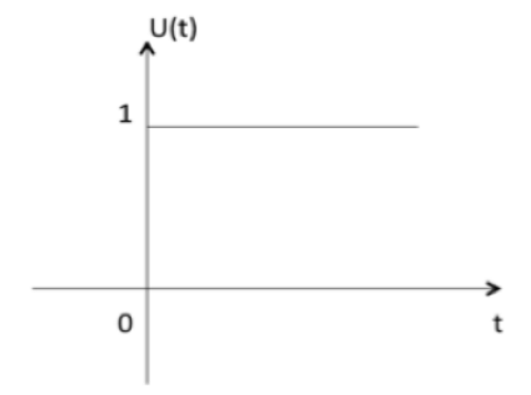
单位斜坡信号	\(r(t)=tu(t)=\begin{cases}t,t≥0 \\0,t>0 \end{cases}\)	\(r(s)=\frac{1}{s^2}\)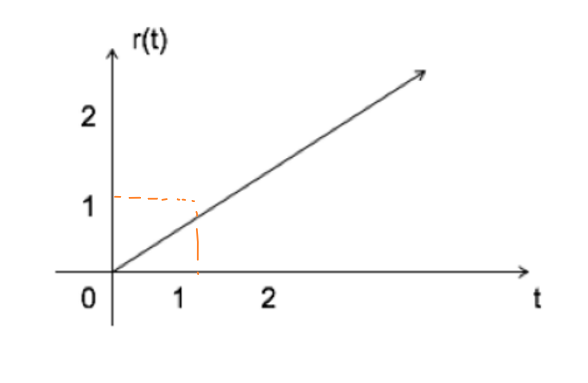
单位圆锥信号	\(x(t)=\begin{cases}\frac{1}{2}t^2,t≥0 \\0,t>0 \end{cases}\)	\(x(s)=\frac{1}{s^3}\)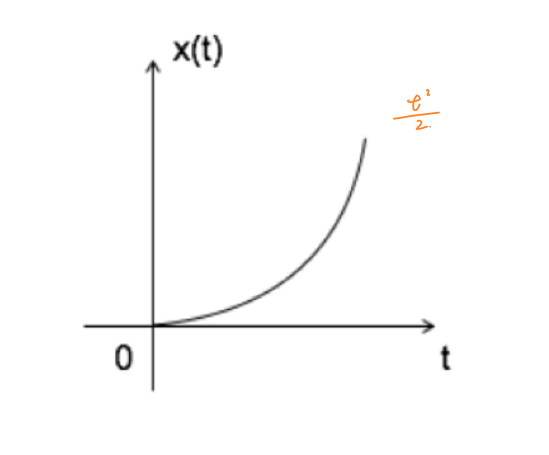

瞬态响应分析

对系统进行瞬态响应分析时，应当对系统的转换方程进行分析。

一阶系统的瞬态响应分析

一阶系统框图如下图所示，该框图可以被化简为开环系统：

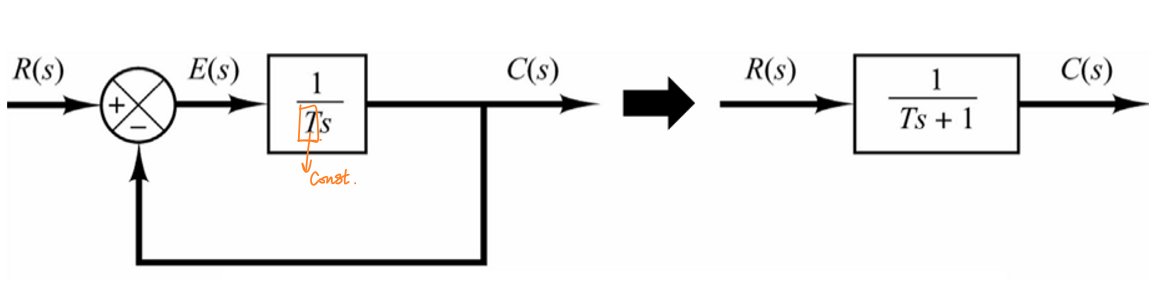
一阶系统的转换方程为：
\[T(s)=\frac{1}{Ts+1}\] 其中\(T\)是一个常数。

单位阶跃响应

带入输入为单位阶跃信号，即\(R(s)=\frac{1}{s}\)，求得：
\[C(s)=\frac{1}{(Ts+1)s}\] 利用部分分式展开求得\(C(s)\)的拉普拉斯反变换：
\[c(t)=1-e^{-\frac{t}{T}},t≥0\] 可以发现\(c(0)=0\)，\(\lim_{t→∞}c(t)=1\)，\(c(t)\)的图像整体是一条从0出发，渐近线为1的指数曲线：

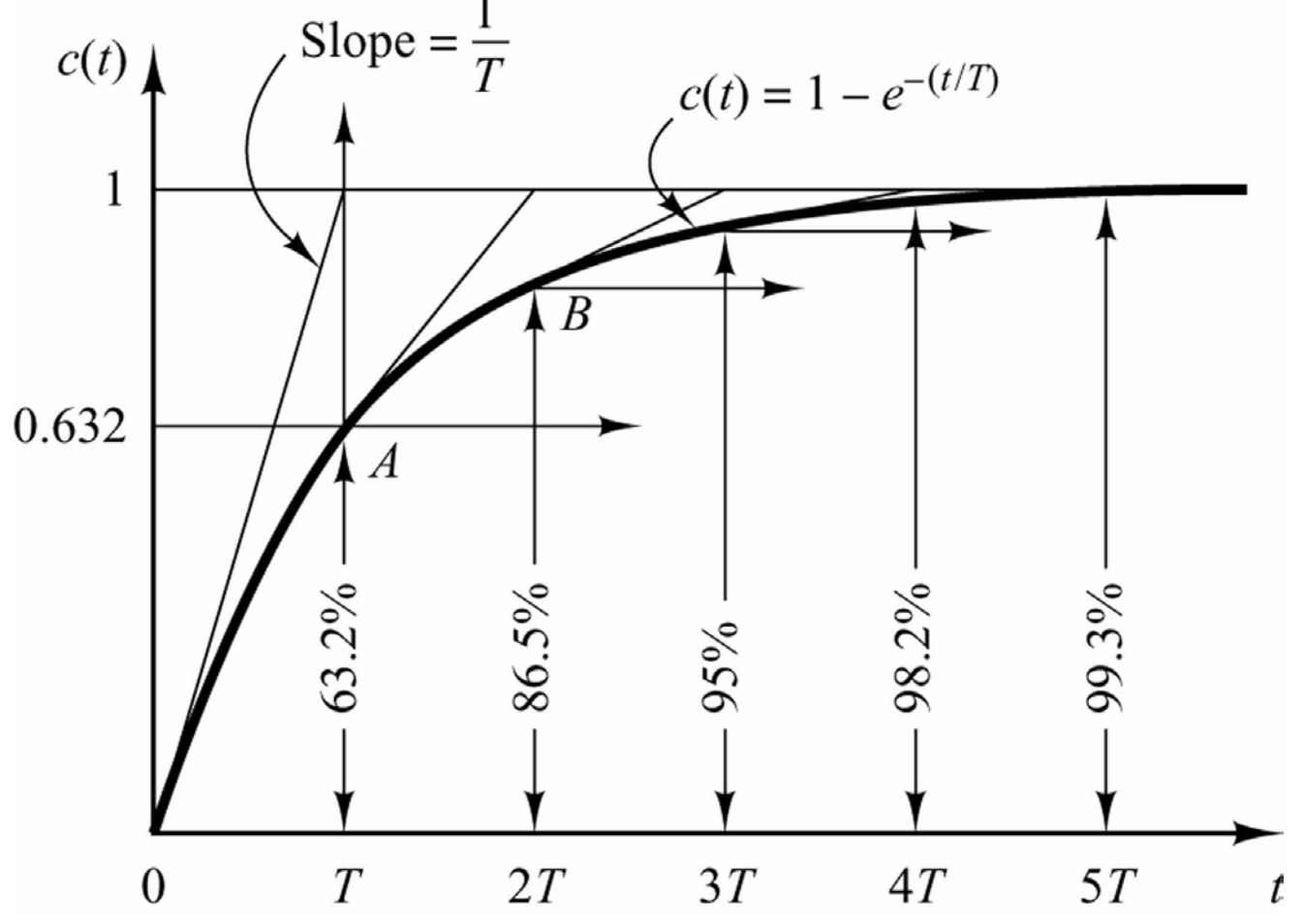
根据图像可以发现：
- \(t=T\)时，\(c(T)=0.632\)，\(t=5T\)时，\(c(T)=0.993\)，此时可以认为系统已经达到最大峰值。
- 图像在\(t=0\)时的斜率为：\(\frac{d}{dt}c(t)|_{t=0}=\frac{1}{T}\)

系统的其他类型响应

相同地，带入\(R(s)=\frac{1}{s^2}\)、\(R(s)=1\)对应求得其单位斜坡响应和单位冲激响应。

对于线性系统而言，系统的单位斜坡响应也可以通过在时域对系统的单位阶跃响应在0到t上积分得到：
\[c_{ramp}(t)=\int_0^tc_{step}(t)dt\] 同样地，线性系统的单位冲击响应也可以通过在时域对系统的单位阶跃响应求导得到：
\[c_{impluse}(t)=\frac{d}{dt}c_{step}(t)\]

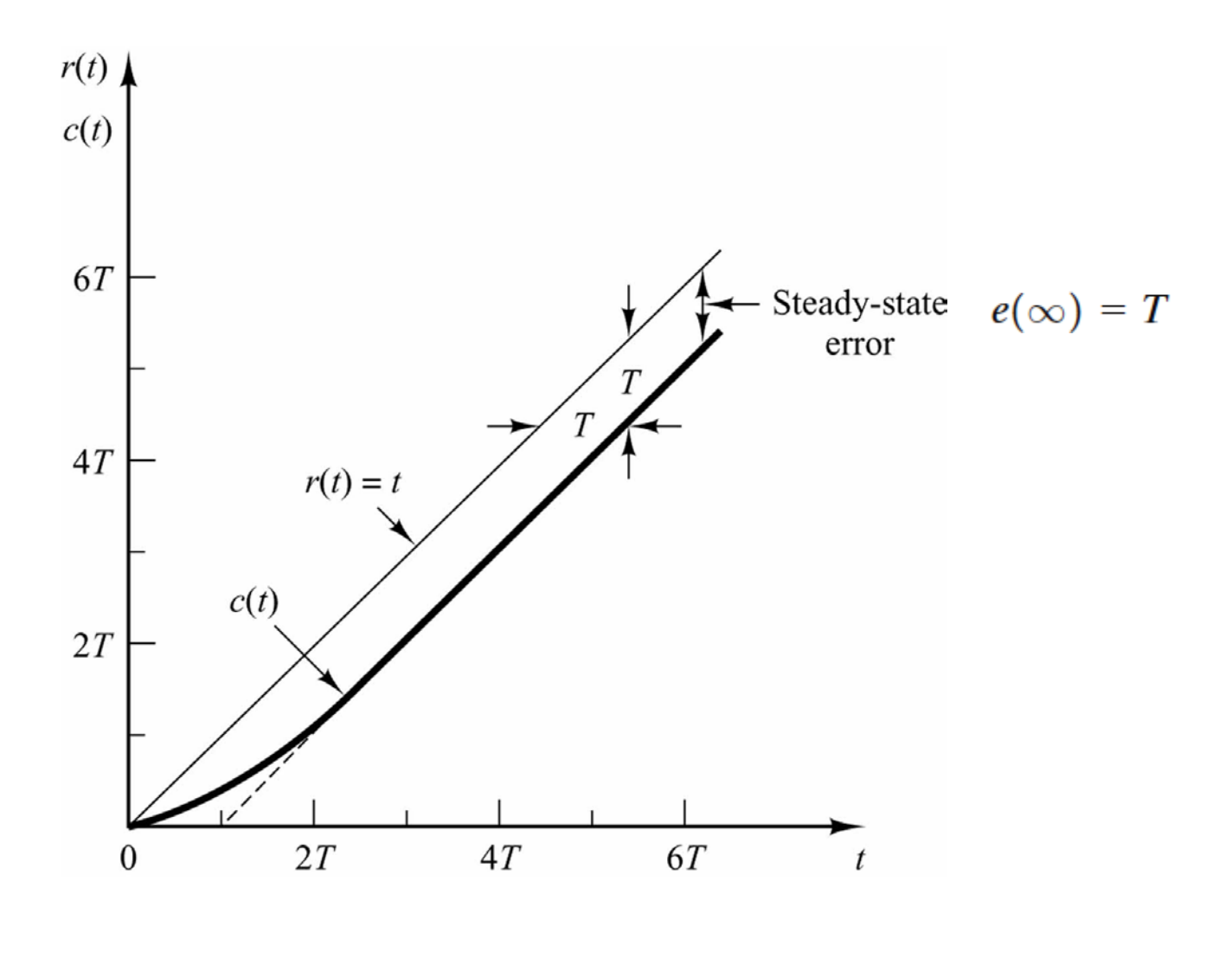
对系统单位斜坡响应：\(c(t)=t-T+Te^{-\frac{t}{T}},t≥0\)，其误差最终(即稳态误差)会趋近于\(T\):

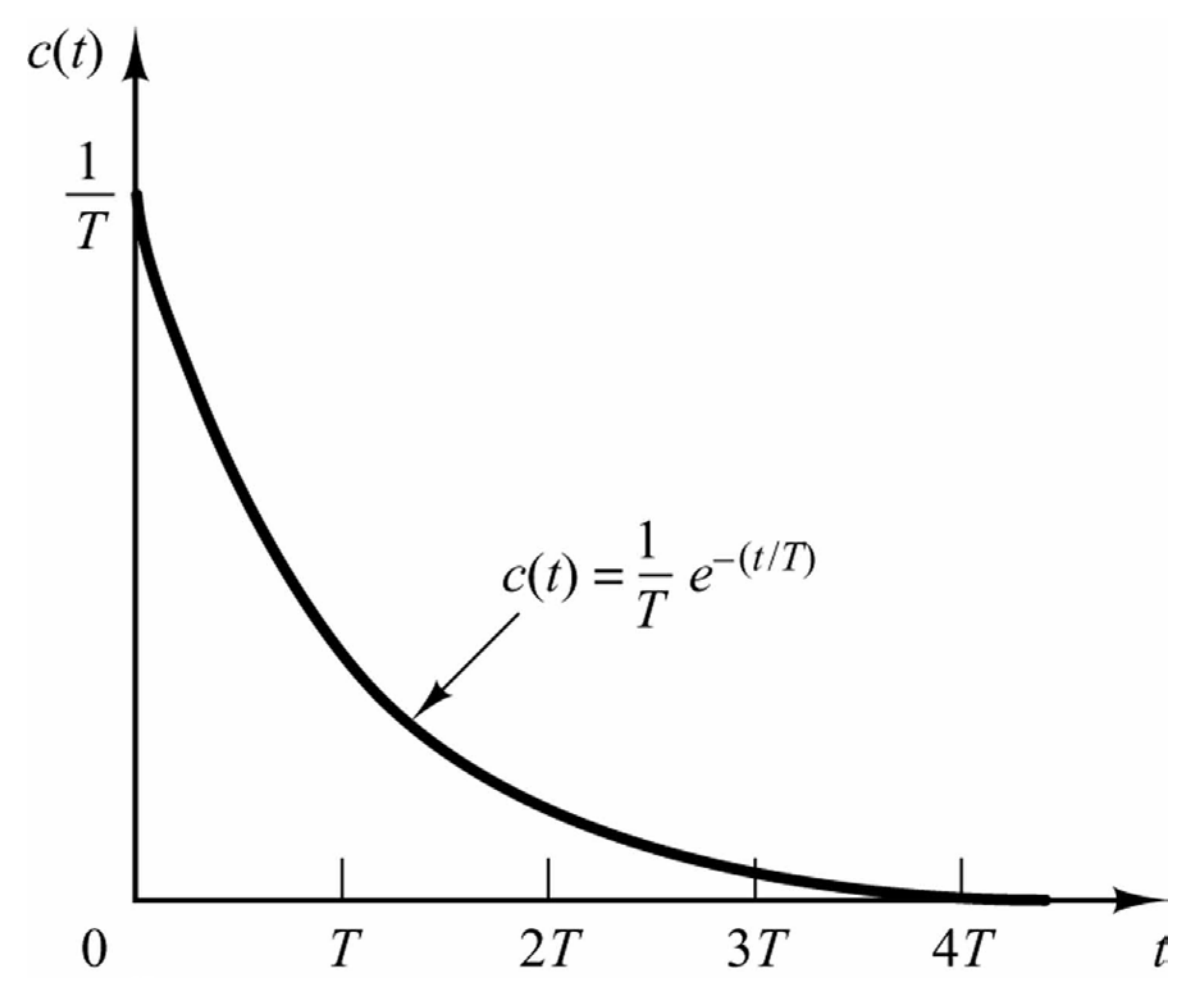
系统的单位冲激响应的可通过系统的转换方程的反拉普拉斯变换得到，单位冲激响应为：\(c(t)=\frac{1}{T}e^{-\frac{t}{T}},t≥0\)：

二阶系统的瞬态响应分析（控制系统视角）

最经典的二阶系统是伺服系统（Servo system/servomechanism），它是一种通过力学装置实现的反馈控制系统，伺服系统通过反馈控制达到对一个机械系统的位置、速度和加速度的控制。伺服系统由伺服控制器\(K\)，负载(包括惯性\(J\)和粘性摩擦\(B\))组成，系统模型可以表示为：

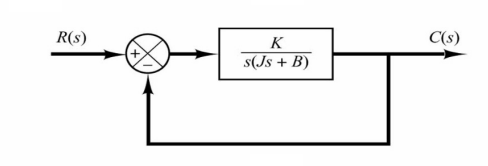
系统转换方程为：
\[T(s)=\frac{K}{Js^2+Bs+K}\] 其中判别式\(Δ=B^2-4JK\)决定了极点的分布情况。
伺服系统是一种机械装置。在结构力学中，定义材料的固有频率\(ω_n\)、衰减\(σ\)和阻尼比（damped ratio）\(ζ\)与上述参数存在下列关系：
\[\frac{K}{J}=ω^2_n,\frac{B}{J}=2ζω_n=2σ\]

结构力学视角下的二阶伺服系统瞬态分析过程请参阅:
[如何理解单自由度系统振动-知乎]https://zhuanlan.zhihu.com/p/263045899
推荐查阅以便获得对本小节形象化的理解。

带入可以得到：

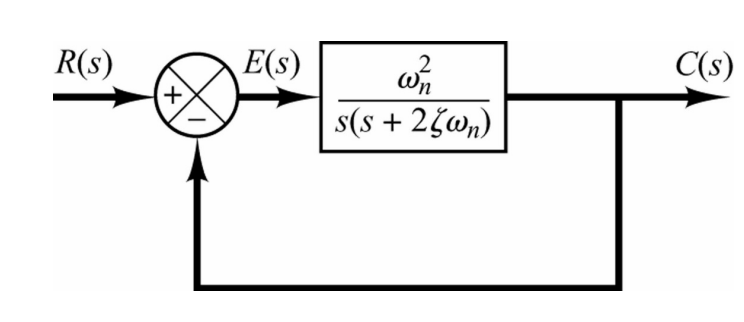
系统的转换方程为：
\[T(s)=\frac{ω_n^2}{s^2+2ζω_ns+ω_n^2}\]

信号与系统中对于阻尼比的定义，对于二阶系统的特征多项式：\((s+p_1)(s+p_2)\)，可以整理出\(s^2+2ζω_ns+ω_n^2\)的形式，其中\(ζ\)为阻尼比(Damping ratio)，\(ω_n\)称为系统的固有频率(Nature Frequency)。

此时使用判别式进行检验，当\(B^2=4JK\)时，计算得到\(\frac{B}{J}=4\frac{K}{B}\)，带入阻尼比等参数，最终得到\(ζ=1\)。可以发现，极点的分布始终只与\(ζ\)与0、1的关系有关。
根据阻尼比的不同，可以分为\(ζ=0\)（零阻尼，Undamped），\(0<ζ<1\)(欠阻尼，underdamped)，\(ζ=1\)(临界阻尼，critically damped)和\(ζ>1\)（过阻尼，over damped）四种情况。

单位阶跃响应

带入\(R(s)=\frac{1}{s}\)，得到系统的单位阶跃响应：
\[\begin{aligned} C(s)=&\frac{ω_n^2}{(s^2+2ζω_ns+ω_n^2)s}\\ =&\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+ω_d^2}-\frac{ζω_n}{(s+ζω_n)^2+ω_d^2} \end{aligned}\] 其中\(ω_d\)称为阻尼固有频率\(ω_d=ω_n\sqrt{1-ζ^2}\)。

• 零阻尼：\(ζ=0\)
  \(ζ=0\)时，根据判别式得出，全部的极点都位于s域的虚轴上。
  此时对其做反变换得到：
  \[c(t)=1-cosω_nt,t≥0\]
• 欠阻尼：\(0<ζ<1\)
  此时特征方程的根由实部和虚部组成，极点在s域左半平面上。
  反变换结果为：
  \[c(t)=1-\frac{e^{-ζω_nt}}{\sqrt{1-ζ^2}}sin(ω_dt+arctan\frac{\sqrt{1-ζ^2}}{ζ})\] 同理，可以通过拉普拉斯反变换得到其他两种情况的系统输出方程，并且根据特征方程的根的情况找到极点在s域的分布。四种情况如下图所示：
  

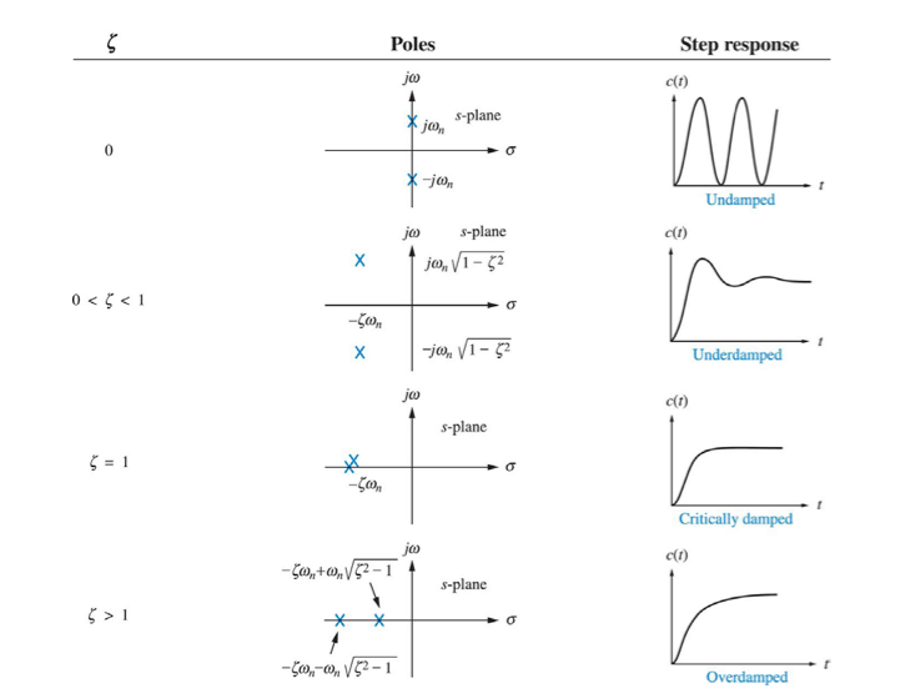
可以发现，相比于其他情况，临界阻尼时系统达到稳定用时最短；而过阻尼时系统的响应总是滞后于输出；系统在零阻尼状态下永远不可能稳定。

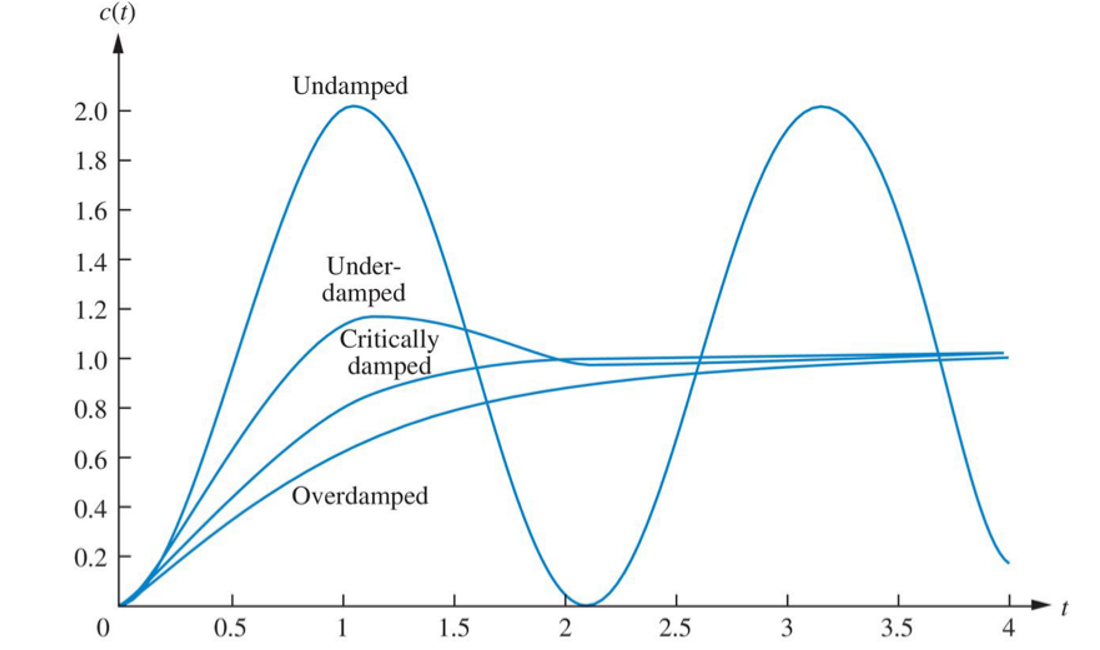
欠阻尼情况的分析

阻尼比在传输线理论中的意义是反映了负载吸收能量与发射能量之间的关系。
如果负载阻抗大于传输线的特征阻抗，那么负载端多余的能量就会反射回源端，由于负载端没有吸收全部能量，故称这种情况为欠阻尼。
如果负载阻抗等于传输线的特征阻抗，即阻抗匹配，那么负载正好吸收发射源发射的全部能量，这种情况是临界阻尼。
如果负载阻抗小于传输线的特征阻抗，负载消耗比当前源端提供的能量更多的能量，故通过反射来通知源端输送更多的能量，这种情况称为过阻尼。
通信工程中经常遇到的是欠阻尼情况。在欠阻尼的情况下，系统特征方程的根为：
\[s=-ζω_n±jω_n\sqrt{1-ζ^2}\] 定义滞后角\(β=arctan\frac{\sqrt{1-ζ^2}}{ζ}\):

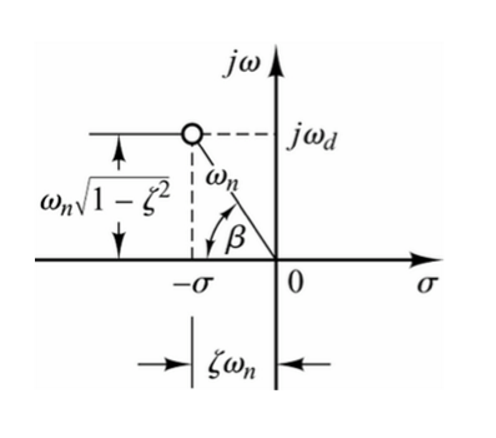
有如下衡量系统达到稳定性快慢的指标：
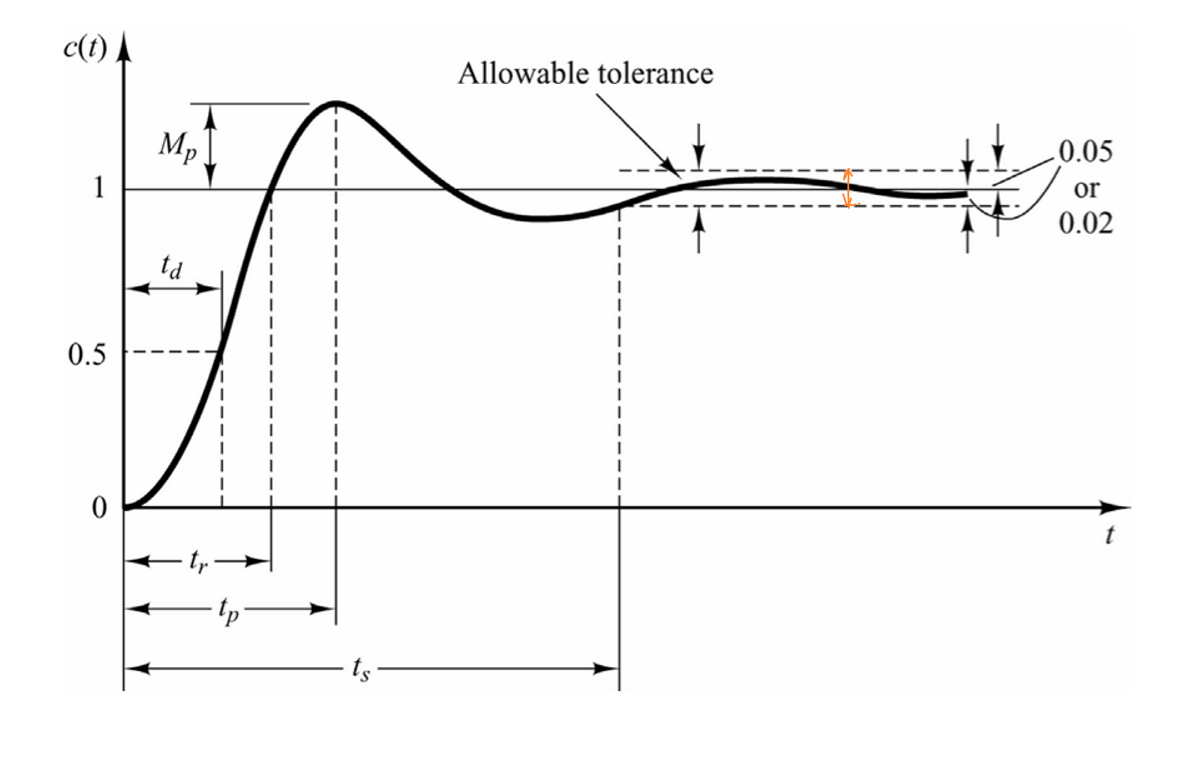
- 上升时间\(t_r\)（rise time）：对于二阶过阻尼系统，定义为阶跃响应曲线从稳态值的10%上升到90%所需的时间。对于二阶欠阻尼系统，也可定义为响应从0第一次上升到终值所需的时间。
令\(c(t)=1\)，得到\(t=\frac{kπ-β}{ω_d},k∈Z^*\).
\[t_r=\frac{π-β}{ω_d}\] - 滞后时间\(t_d\)（delay time）：系统响应第一次达到0.5倍终值时所需要的时间。
- 峰值时间\(t_p\)（peak time）：阶跃响应曲线越过稳态值达到第一个峰值所需要的时间。
根据导数在极值点为0可以得到：
\[\begin{aligned} \frac{dc(t)}{dt}&=0\\ &=\frac{e^{-ζω_nt}}{\sqrt{1-ζ^2}}[ζω_nsin(ω_dt+β)-ω_dcos(ω_dt+β)] \end{aligned}\] 由于\(\frac{e^{-ζω_nt}}{\sqrt{1-ζ^2}}≠0\)，解得\(ω_dt+β=kπ+arctan\frac{ω_d}{ζω}\).
最终得到：
\[t_p=\frac{π}{ω_d}\] 此时峰值为:
\[c(t_p)=1+e^{-\frac{πζ}{\sqrt{1-ζ^2}}}\] - 调节时间\(t_s\)(settling time)：阶跃响应曲线达到并永远保持在一个允许误差范围(误差带：通常取±5%或±2%)内，所需的最短时间。
\[t_s=4T=\frac{4}{ζω_n}(\text{达到0.98})\] \[t_s=3T=\frac{3}{ζω_n}(\text{达到0.95})\]
- 超调量/过冲率\(M_p\)（maximum perent overshoot）：阶跃响应曲线的最大偏离量\(c(t_p)\)与终值之差的百分比。
\[M_p=\frac{c(t_p)-c(∞)}{c(∞)}×100\%,c(∞)=1\] \[M_p=e^{-\frac{πζ}{\sqrt{1-ζ^2}}}×100\%\]

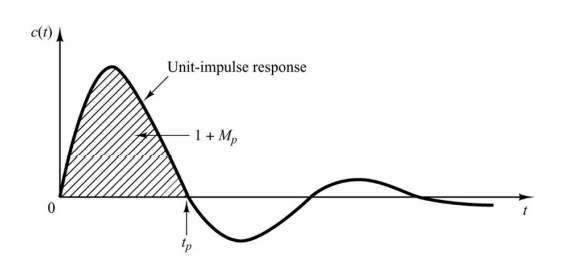
由于线性系统的单位冲激响应和单位阶跃响应互为导数关系，因此在单位冲激响应第一次达到零时，对应峰值时间，此时累计时间面积最大，对应峰值\(1+M_p\)。

稳态响应分析

系统的稳定性

系统要具有稳定性，对系统的稳态响应分析才有意义。系统的稳定性分为绝对稳定性和相对稳定性，绝对稳定性则是根据稳定性定义直接判断当时间趋于无穷时系统时候收敛，而相对稳定性(relative stability)关注的是系统达到稳定的快慢。
相对稳定性可以通过调节时间\(t_p\)反映，\(t_p\)越长则系统达到稳定的时间越长。此外，在\(s\)域上，系统的极点分布越远离虚轴，系统达到稳定的时间越短。

劳斯–赫尔维茨稳定性判据/劳斯判据

劳斯–赫尔维茨稳定性判据/劳斯判据(Routh–Hurwitz stability criterion)是控制理论中的一个数学判据，是线性时不变系统稳定的充分必要条件。
对于n阶系统的特征多项式：
\[D(n)=a_ns^n+a_{n-1}s^{n-1}+...+a_1s+a_0\] 以下列递推方法计算：
\[b_i=\frac{a_{n-1}×a_{n-2i}-a_n×a_{n-(2i +1)}}{a_{n-1}}\] \[c_i=\frac{b_1×a_{n-2i}-a_{n-1}×b_{i +1}}{b_{1}}\] \[...\] 带入如下的劳斯表中：

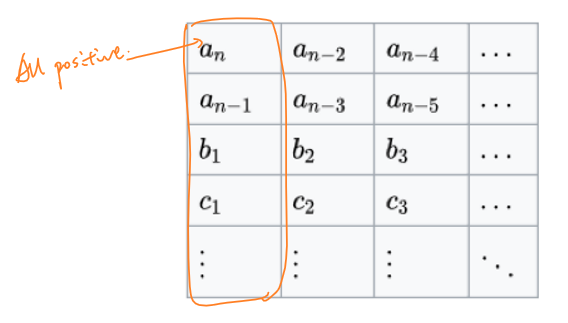
对劳斯表的每一行提取公因式化简，如果化简后的劳斯表中的第一列全为正，则该LTI系统是稳定系统。

常用的劳斯表元素：
\[b_1=-\frac{1}{a_{n-1}}\left|\begin{matrix} a_n & a_{n-2}\\ a_{n-1} & a_{n-3} \end{matrix}\right|\] \[b_2=-\frac{1}{a_{n-1}}\left|\begin{matrix} a_n & a_{n-4}\\ a_{n-1} & a_{n-5} \end{matrix}\right|\] \[c_1=-\frac{1}{b_{1}}\left|\begin{matrix} a_{n-1} & a_{n-3}\\ b_1 & b_2 \end{matrix}\right|\]

稳定系统的前向传递函数和稳态类型

对于稳定系统当时间趋于无穷时，系统达到稳定。此时传递函数退化为前向传递函数\(G(s)\).
因此稳态响应的分析是基于前向传递函数的。
系统的前向传递函数可以表示为：
\[G(s)=\frac{K(T_as+1)(T_bs+1)...(T_ms+1)}{s^v(T_1s+1)(T_2s+1)...(T_ps+1)}\] 根据前项传递函数的分母的\(s^v\)对系统进行分类：前项传递函数的分母为分母的\(s^v\)则系统为\(v\)型系统(V-type system)，是系统在s域上的重极点数目。其物理意义是开环传递函数中含有的积分环节的个数。工程上按照\(v\)的值分别称系统为0型，1型，2型，\(v>2\)的系统实际上极少遇到，因为含有多于两个积分单元的系统很难使之稳定，因此一般情形下只使用0型，1型和2型的系统。

稳态误差

对稳定的系统计算稳态误差才有意义。

根据误差比的定义：\(\frac{E(s)}{R(s)}=\frac{1}{1+G(s)}\), 可以得到：
\[E(s)=\frac{1}{1+G(s)}R(s)\] 由稳态误差的定义：\(e_{ss}=\lim_{t→∞}e(t)\)，由终值定理：
\[e_{ss}=\lim_{s→0}sE(s)=\lim_{s→0}\frac{sR(s)}{1+G(s)}\]

静态误差系数

静态误差系数(static error coefficient)分为静态位置误差系数、静态速度误差系数、静态加速度误差系数。分别代表了控制系统中，一个系统对阶跃输入、斜坡输入、抛物线信号输入响应消除或减少稳态误差的能力。当系统输入信号形式、输出量的期望及容许的稳态位置误差确定后，可以方便的根据静态误差系数去选择系统的型别和开环增益，进行控制系统设计。但是静态误差系数仅对单位反馈控制系统有着明确的物理意义。
- 静态位置误差系数(static position error constant)
定义静态位置误差系数\(K_p\)表示各型系统在阶跃输入\(r(t)=Ru(t)\)作用下的位置误差，其中\(R\)为输入阶跃函数幅值。
可以计算得出稳态误差为：
\[e_{ss}(∞)=\begin{cases} \frac{R}{1+K},v=0\\ 0,v≥1 \end{cases}\] 在单位阶跃输入\(r(t)=u(t)\)（即\(R(s)=\frac{1}{s}\)）作用下，其稳态误差是期望输出1和实际输出\(\frac{K}{1+K}\)之间的位置误差，定义为： \[K_p=\lim_{s→0}G(s)=G(0)=\lim_{s→0}\frac{K}{s^v}\]

• 静态速度误差系数(static velocity error constant)
  在速度输入作用下，即\(r(t)=Rt\)，其中\(R\)为输入速度函数斜率，可以算出稳态误差为:
  \[e_{ss}(∞)=\begin{cases} ∞,v=0\\ \frac{R}{K},v=1\\ 0,v≥2 \end{cases}\] 定义静态速度误差系数：
  \[K_v=\lim_{s→0}sG(s)=\lim_{s→0}\frac{K}{s^{v-1}}\]

• 静态加速度误差系数(static acceleration error constant)
  在加速度输入作用下，即\(r(t)=\frac{1}{2}Rt^2\)，其中\(R\)为输入加速度函数速度变化率，可以算出稳态误差为：
  \[e_{ss}(∞)=\begin{cases} ∞,v=0,1\\ \frac{R}{K},v=2\\ 0,v≥3 \end{cases}\] 定义静态加速度误差系数：
  \[K_a=\lim_{s→0}s^2G(s)=\lim_{s→0}\frac{K}{s^{v-2}}\]

可以将三种稳态误差系数总结表格如下：

系统类型	位置误差 \(r(t)=1\) \(K_p=\lim_{s→0}\frac{K}{s^{v}}\)	速度误差 \(r(t)=t\) \(K_v=\lim_{s→0}\frac{K}{s^{v-1}}\)	加速度误差 \(r(t)=\frac{1}{2}t^2\) \(K_a=\lim_{s→0}\frac{K}{s^{v-2}}\)
0型	\(\frac{1}{1+K_p}\)	\(∞\)	\(∞\)
I型	\(0\)	\(\frac{1}{K_v}\)	\(∞\)
II型	\(0\)	\(0\)	\(\frac{1}{K_a}\)

非单位反馈系统的瞬态稳态响应分析方法

上述对系统的瞬态稳态响应分析都建立在反馈系数\(H(s)=1\)的条件下，这种系统称为单位反馈系统，当\(H(s)≠1\)时，只需要利用系统框图化简为单位反馈系统即可：

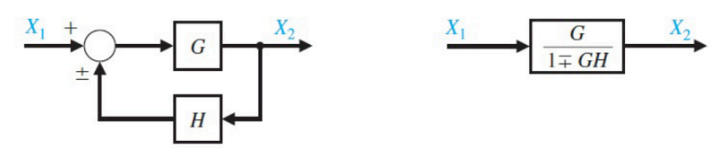
非单位反馈系统的稳态误差系数

• 静态位置误差系数 \[K_p=\lim_{s→0}G(s)H(s)\]
• 静态速度误差系数 \[K_v=\lim_{s→0}sG(s)H(s)\]
• 静态加速度误差系数 \[K_a=\lim_{s→0}s^2G(s)H(s)\]