04. 波特图的绘制和分析·电路实现
本文最后更新于 2025年6月4日 晚上
波特图·电路实现
波特图(Bode plot)是一种直接表示系统幅度值和相位随着频率变化的图像,是最简单的对系统频率响应的可视化工具。其横轴为\(ω\),纵轴为\(|H(jω)|_{dB}\)和\(∠H(jω)\),如下图所示:
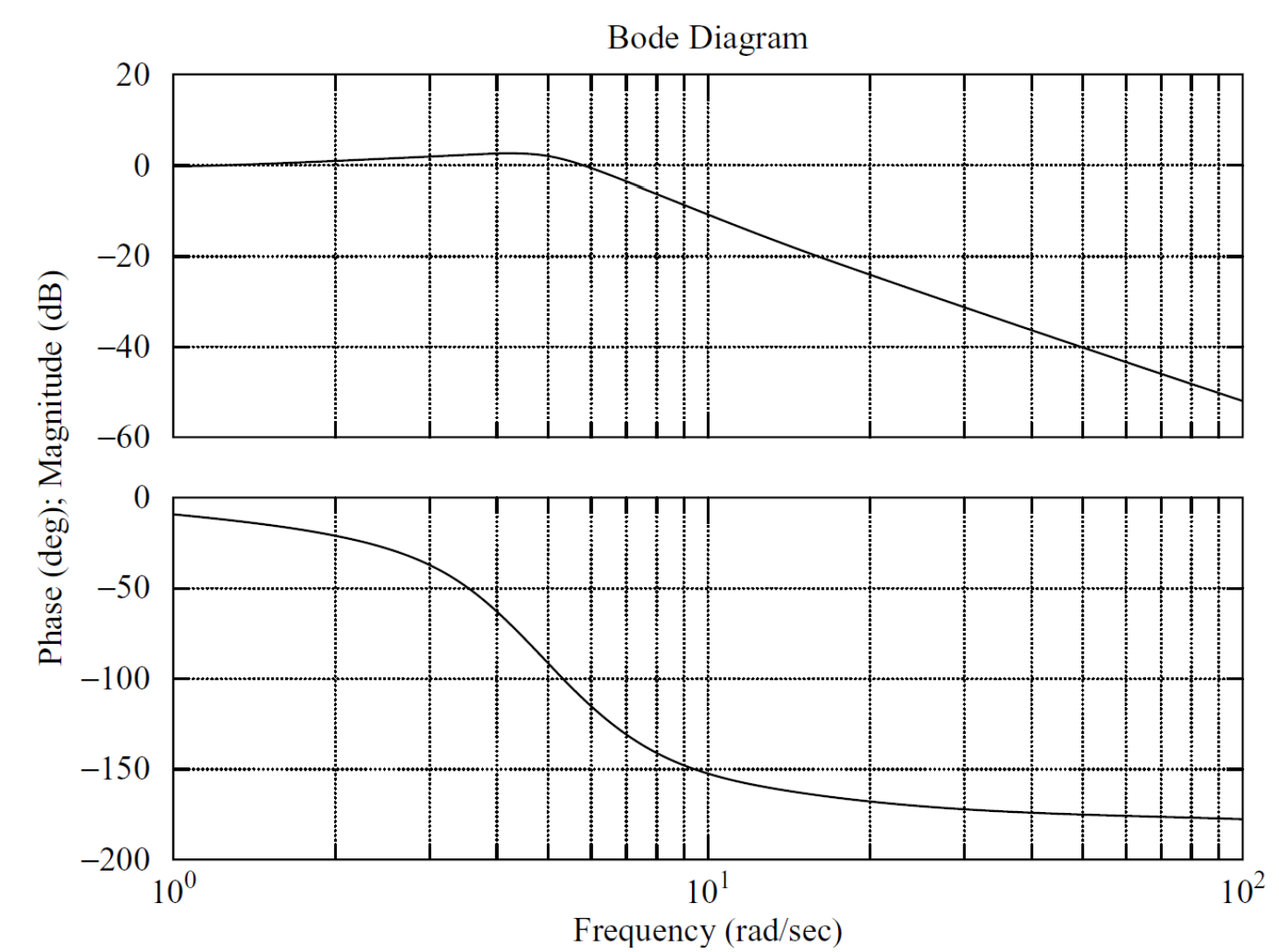
使用MATLAB绘制波特图
在MATLAB中,当系统传递函数已知的情况下,可以使用函数bode()直接生成对应系统的波特图,例如:
1
2
3
4num=[8,18,32] %传递函数的分子系数
den=[1,6,14,24] %传递函数的分母系数
sys=tf(num,den) %构建系统传递函数
bode(sys)
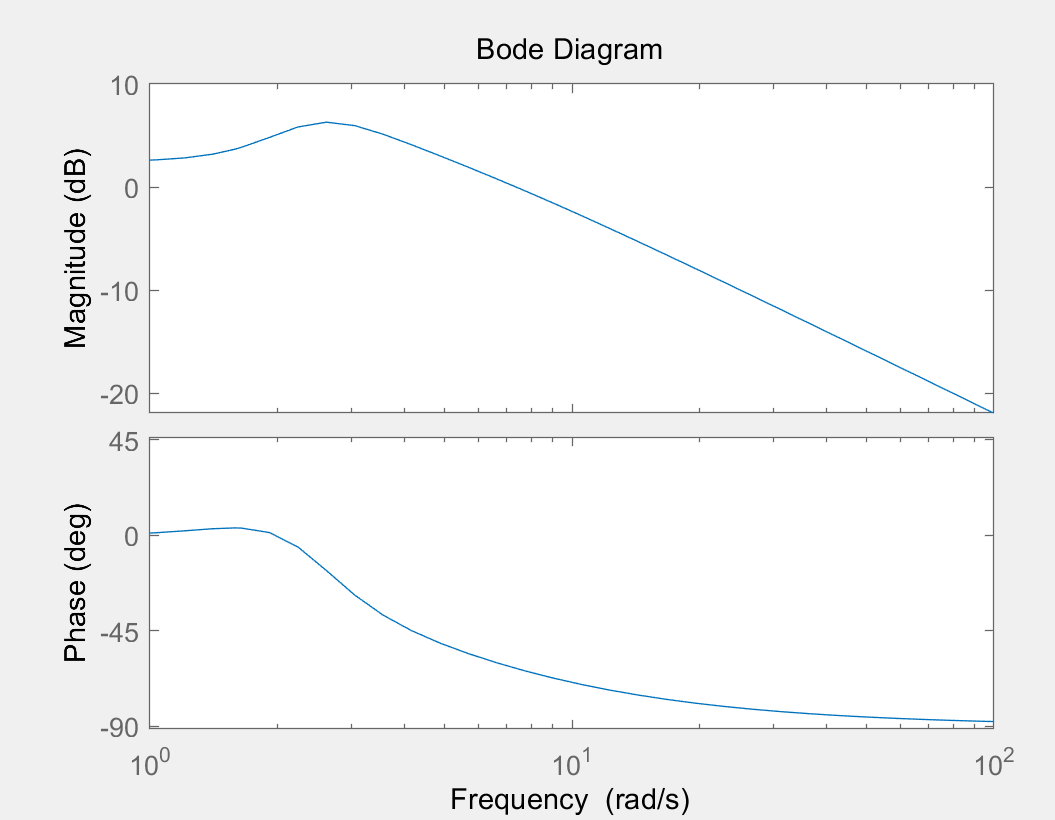
采样法绘制波特图
使用采样来绘制波特图的方法是:
- 令传递函数中的\(s=jω\),得到\(G(jω)\)
- \(G(jω)\)的分子分母同时乘以分母表达式的共轭形式,以化简得到:
\[G(jω)=A(ω)+jB(ω)\] 的形式。
- 取不同的\(ω\)值对其幅频响应和相频响应进行采样,利用采样点绘制波特图。
使用采样绘制波特图的难点是波特图的准确性取决于采样点的数目和采样点的位置。如果传递函数结构复杂,那么计算所有采样点所需要的计算量太大。
渐近线近似绘制的理论基础
渐进线近似法(Asymptotic Bode Plot)是一种将传递函数结构分为若干个区间,对每个区间使用直线来渐进拟合每个区间的频率响应情况。相比于采样法,渐近线近似法的计算量更小,并且渐进误差在可允许的范围内,是一种便捷的手绘波特图的方法。
传递函数的级联形式
对于系统传递函数:
\[H(s)=\frac{K∏(s+z_i)}{∏(s+p_i)}\] 如果将每一个括号的常数项进行归一化,就得到系统传递函数的级联形式:
\[H(s)=\frac{K∏z_i(\frac{1}{z_i}s+1)}{∏p_i(\frac{1}{p_i}s+1))}\]
传递函数的元素及其渐进线近似波特图
对于任意系统的传递函数,其分子分母都由如下几项相乘得到:
- 常数项\(K\):称为增益
- \(s\):称为积分环节(分母)或者微分环节(分子)
- 一阶项\((s+1)\):称为惯性环节(分母)
- 二阶项\((s^2+2ζs+1)\)
通过分别讨论这几个元素的波特图,进而可以推理出任意传递函数的波特图。
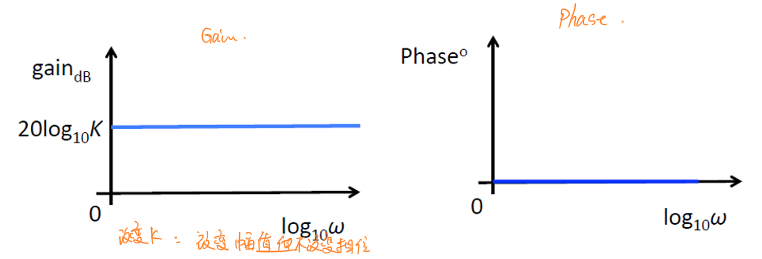
常数项\(K\)
常数项\(K\)在波特图上表示时,其幅值和相位都不随着频率而变化,其幅值恒定为\(20lgK\),相位恒定为\(0°\)不变。
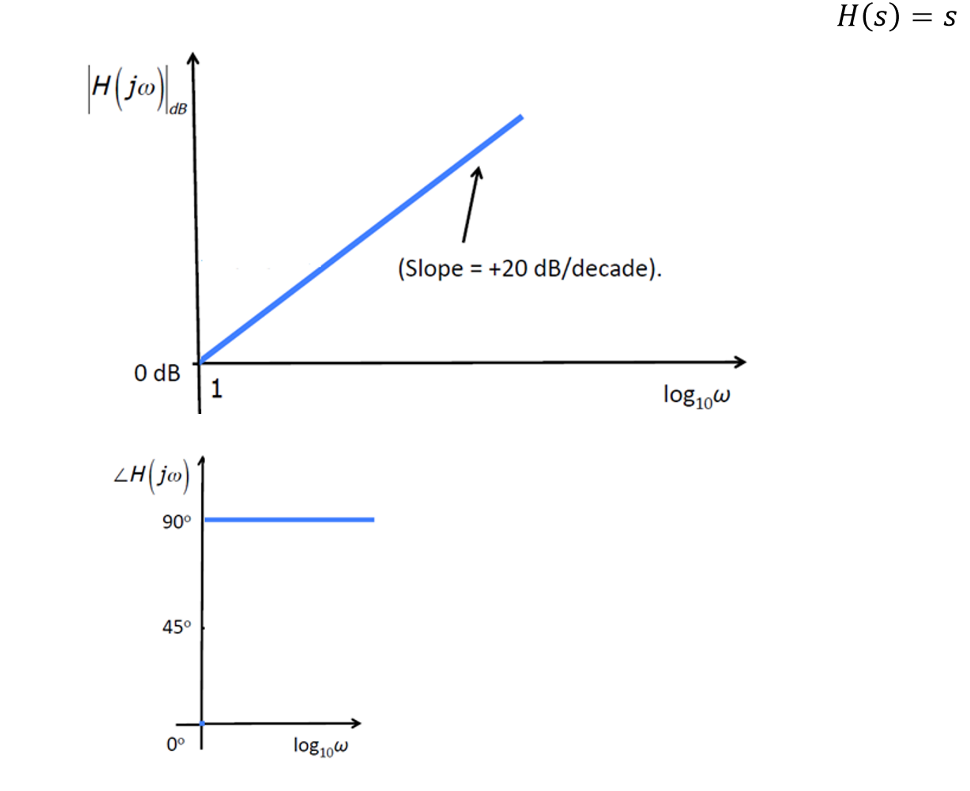
\(s\)
对分子中的\(s\)项(表示为\(s^{+1}\)):
幅值: \(20lg(s)=20lg(ω_0)\),\(ω_0\)表示作图的起始频率。当波特图的横轴为\(lg(ω)\)时,其在波特图上为从零点向上,斜率为\(20dB/decade\)的直线。
相位:\(arctan(\frac{ω}{0})=90°\),其相位恒定为90°不变。
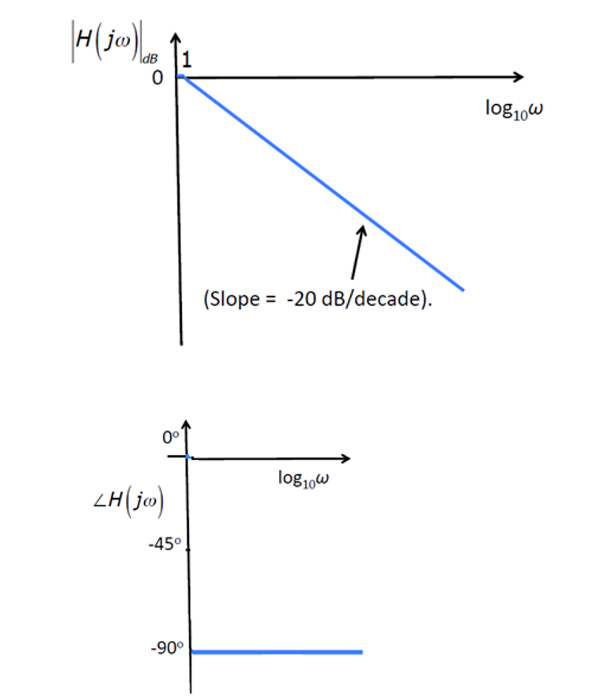
对分母中的\(s\)项(表示为\(s^{-1}\)):
幅值: \(20lg(\frac{1}{s})=-20lg(ω_0)\),当波特图的横轴为\(lg(ω)\)时,其在波特图上为从零点向下,斜率为\(-20dB/decade\)的直线。
相位:\(-arctan(\frac{ω}{0})=-90°\),其相位恒定为-90°不变。
注意,使用对数方格纸作图时,需要选取起始频率\(ω_0\)(横轴原点为:0.1rad/s或者0.001rad/s),如果存在\(s\)项,波特图的起始幅值应当为:
\[±20lg(ω_0)+20lg(K)\] \(+20lg(ω_0)\):\(s\)位于分子;\(-20lg(ω_0)\):\(s\)位于分母。
对数方格纸的横轴是非均匀的,表示其坐标轴上数值对数分布,横轴是均匀的数值分布。因此,对于坐标轴横轴上的两个点:\(x_1\)、\(x_2\)。满足关系:
\[k(x_1-x_2)=y(x_1)-y(x_2)\] 其中\(k\)称为对数斜率:
\[k=\frac{y(x_1)-y(x_2)}{x_1-x_2}\] 单位为\(dB/decade\)。
一阶项\((Ts+1)\)
对\((\frac{s}{T}+1)^{+1}\):
幅值:\(20lg(1+jωT)=20lg(\sqrt{1+ω^2T^2})\),其波特图近似为:- 当\(0<ω<\frac{1}{T}\),幅值为0
- 当\(ω>\frac{1}{T}\),幅值为\(20lg(ω)\)
相位:\(arctan(ωT)\),其波特图近似为:
当\(0<ω<\frac{0.1}{T}\),相位为0°
当\(\frac{0.1}{T}<ω<\frac{10}{T}\),斜率为\(5°T\)(\(45°/decade\))的直线
当\(ω>\frac{10}{T}\),相位为90°
同理,\((\frac{s}{T}+1)^{-1}\)的波特图如下图所示:
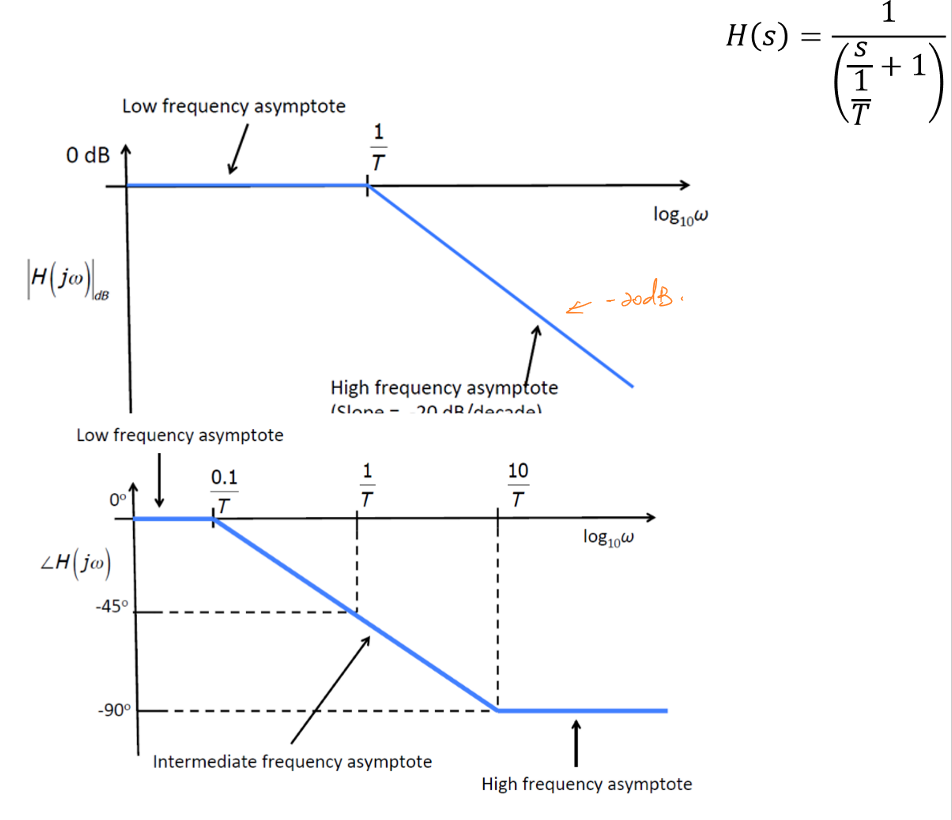
- 当\(0<ω<\frac{1}{T}\),幅值为0
二阶项\((s^2+2ζs+1)\)
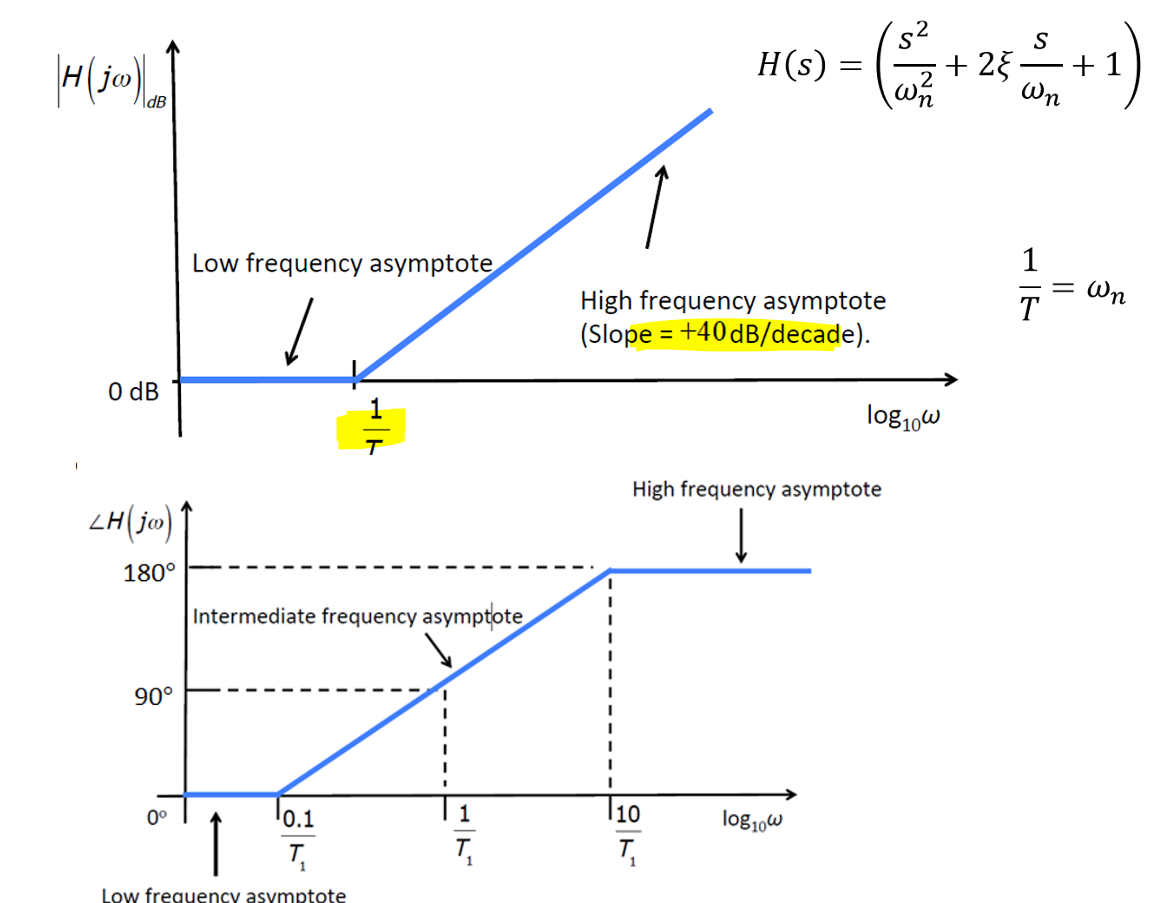
对\((\frac{s^2}{ω_n^2}+2\frac{ζ}{ω_n}s+1)^{+1}\),有: \[\frac{1}{T}=ω_n\]
幅值:\(20lg(\sqrt{(1-\frac{ω^2}{ω_n^2}+(2ζ\frac{ω^2}{ω_n^2}))})\),其波特图近似为:- 当\(0<ω<\frac{1}{T}\),幅值为0
- 当\(ω>\frac{1}{T}\),幅值为\(40lg(ω)\)
相位:\(arctan\frac{2ζ\frac{ω}{ω_n}}{1-\frac{ω}{ω_n^2}}\),其波特图近似为:
- 当\(0<ω<\frac{0.1}{T}\),相位为0°
- 当\(\frac{0.1}{T}<ω<\frac{10}{T}\),斜率为\(10°T\)(\(90°/decade\))的直线
- 当\(ω>\frac{10}{T}\),相位为180°
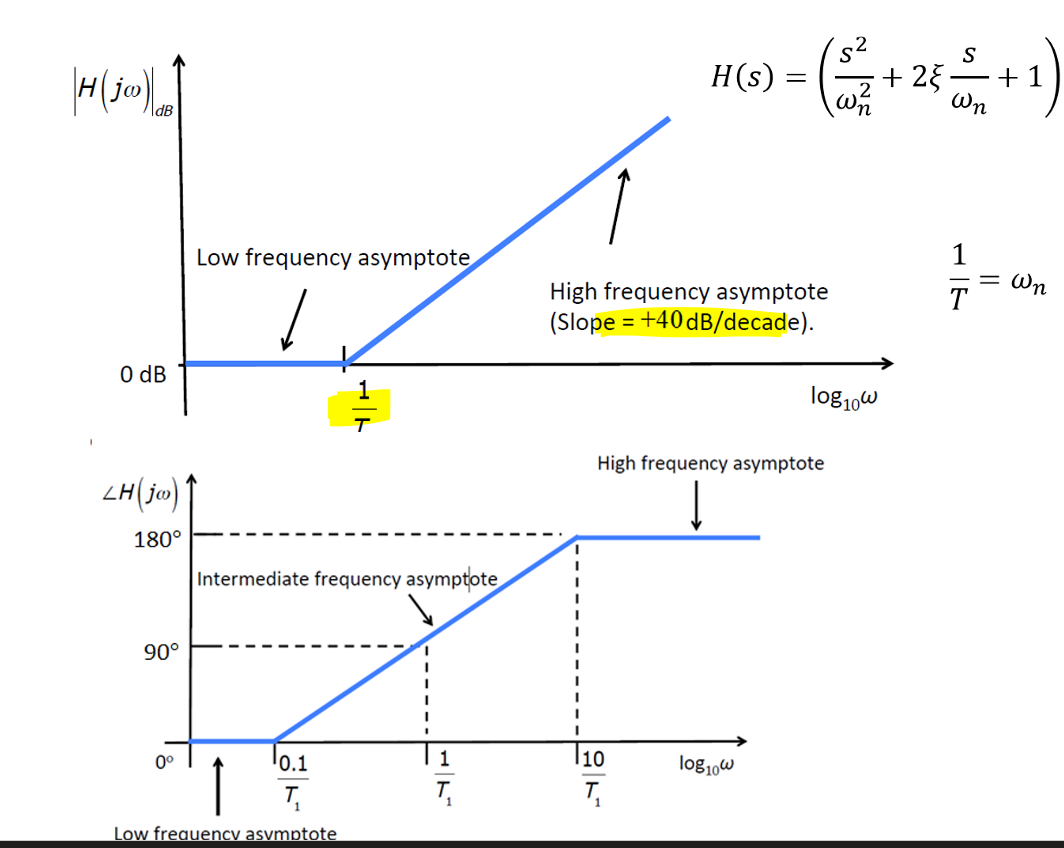
同理,\((\frac{s^2}{ω_n^2}+2\frac{ζ}{ω_n}s+1)^{-1}\)的波特图如下图所示:
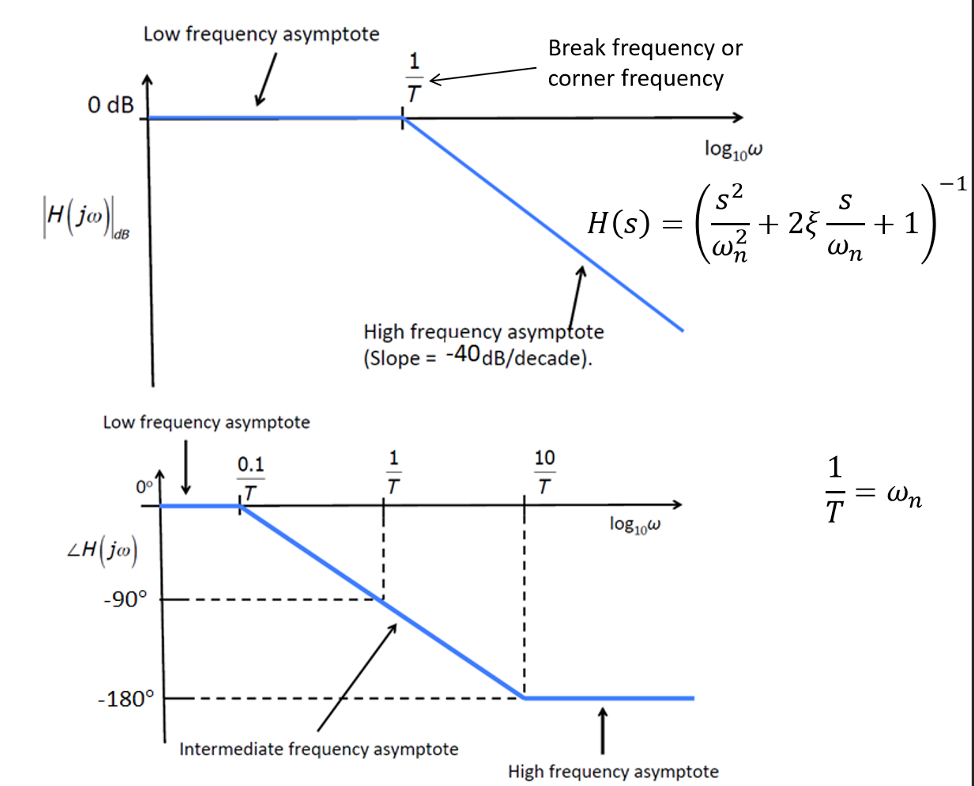
此外,二阶系统由于存在阻尼,在峰值位置\(ω_p\)需要对峰值进行修正:
在峰值处,有\(\frac{d}{dω}|H(jω)|=0\),其中\(ω_p=ω_n\sqrt{1-2ζ^2}\),代回求得峰值为:
\[|H(jω_p)|_{dB}=-20lg(2ζ\sqrt{1-ζ^2})\] 当\(0<ζ<\frac{1}{√2}\)时,可以视为\(ω_p=ω_n\),那么该点的值可以近似为:
\[|H(jω_n)|_{dB}=-20lg(2ζ)\]因此,当\(0<ζ<\frac{1}{√2}\)时,需要在\(\frac{1}{T}\)处增加\(-20lg(2ζ)\)进行修正。
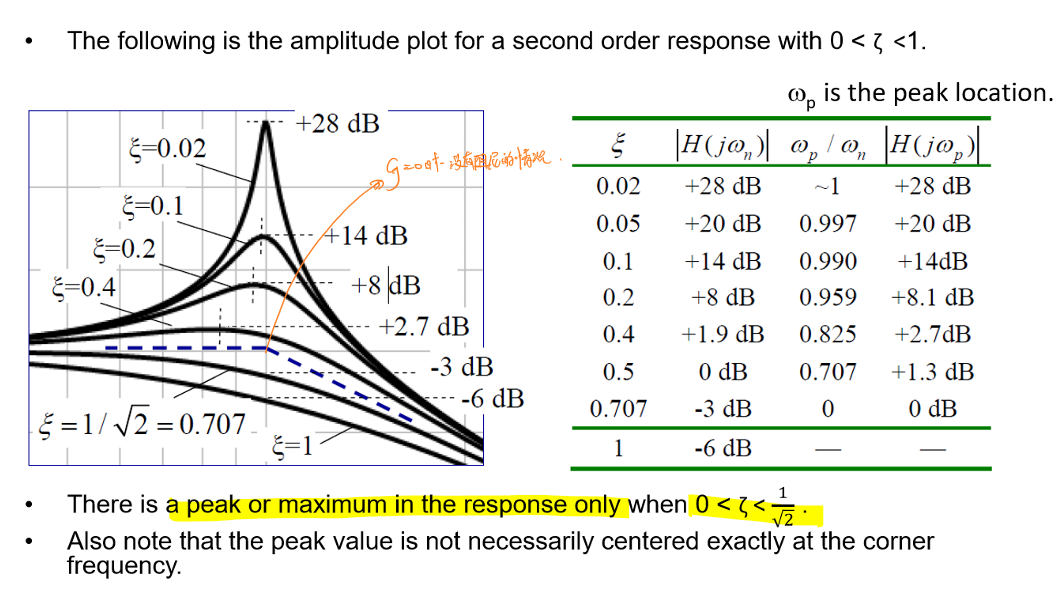
- 当\(0<ω<\frac{1}{T}\),幅值为0
总结
对幅频响应:
- 对每一个\(n\)阶数项,其极点会给幅频响应带来一个\(-20×n dB/decade\)频程斜率的变化;其零点会给幅频响应带来一个\(+20×n dB/decade\)频程斜率的变化。
对相频响应:
对每一个\(n\)阶数项,其极点会在\(ω∈(\frac{0.1}{T},\frac{10}{T})\)提供\(-45°×n /decade\)的斜率变化;其零点会在\(ω∈(\frac{0.1}{T},\frac{10}{T})\)提供\(+45°×n /decade\)的斜率变化。
对每一个\(n\)阶数项,其极点会给相频响应带来一个\(-90°×n\)的相位变化;其零点会给相频响应带来一个\(+90°×n\)的相位变化。
传递函数的级联
对级联系统,其每一个子系统的传递函数为\(F_i(jω)\),有整个系统的传递函数:
\[F(jω)=∏F_i(jω)\] 系统的幅值和相位为:
\[|F(jω)|_{dB}=|F_i(jω)|_{dB}\] \[∠F(jω)=∑∠F_i(jω)\] 可以发现,整个系统的波特图可以通过各子部分的波特图叠加得到。因此,对任何一个传递函数,其整个波特图都可以被分解为若干个元素的波特图的叠加。
绘制渐近线波特图的方法
图形法
- 在对数格纸上画出每一个子部分的波特图
- 将每个部分的波特图叠加,最终得到整个系统的波特图
下面几张图展示了图形法画出\(G(s)=\frac{20s}{s+10}\)的幅值波特图:
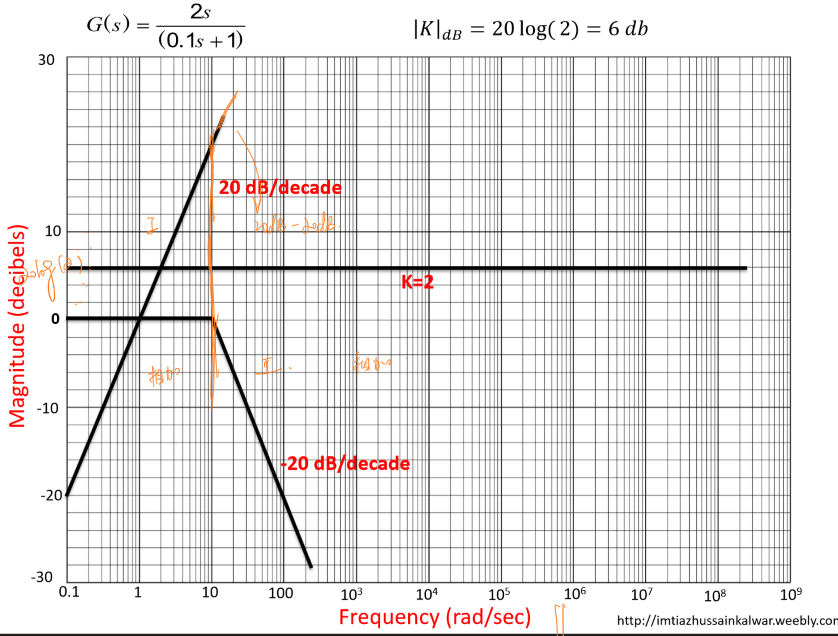
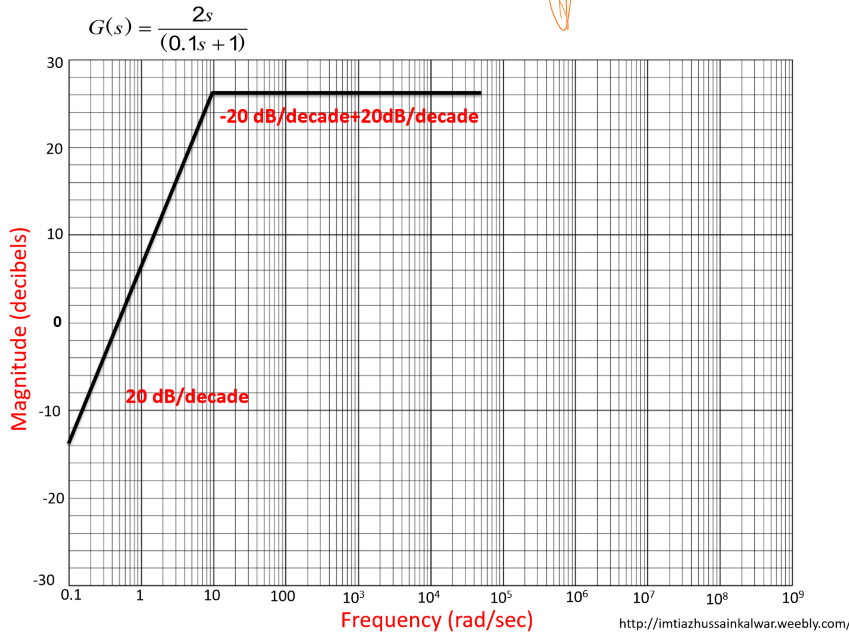
表格法
- 首先将系统传递函数改写为级联形式
- 列出系统传递函数中所有的零点和极点,从小到大排列,从而将整个系统的波特图分为几个区间
- 看系统方程的每个元素在对每段区间波特图的斜率贡献
- 将每个元素的斜率贡献全部叠加,得到系统在每段区间上的斜率。
- 找到初始值。
- 利用:
在区间\((x_1,x_2)\)上,纵轴的变化量\(Δ=y_1-y_2\)可以求得为:
\[Δ=klg\frac{x_2}{x_1}\] 因此每一段区间的起始值为:
\[O=O_{-1}+Δ\] \(O_{-1}\)是上一段区间的起始值。
找到每一段区间的起点。
- 连接所有点,画图。
下表展示了表格法画出\(G(s)=\frac{s+1}{s(0.1s+1)(0.4s+1)}\)的幅值波特图对应的表格:
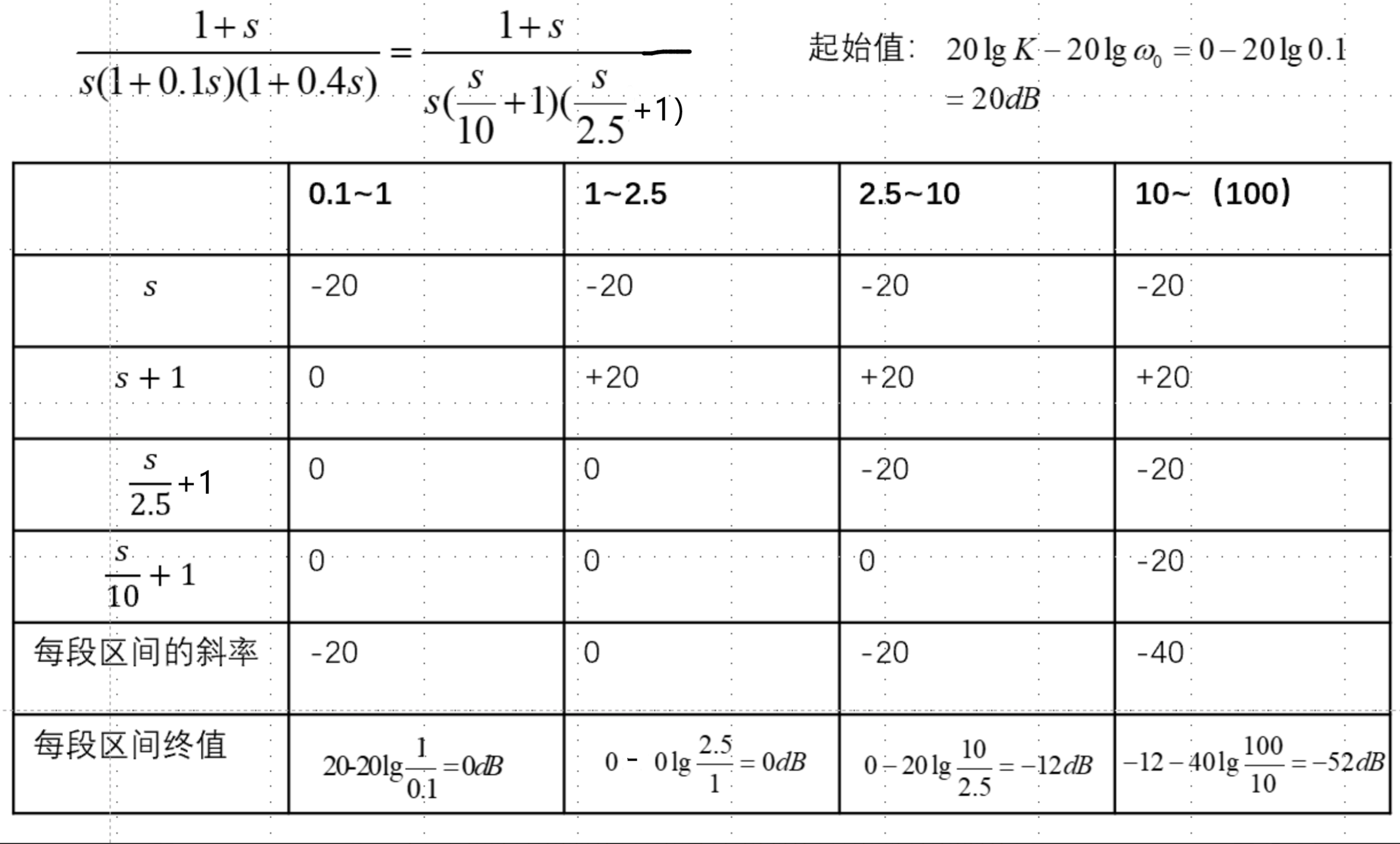
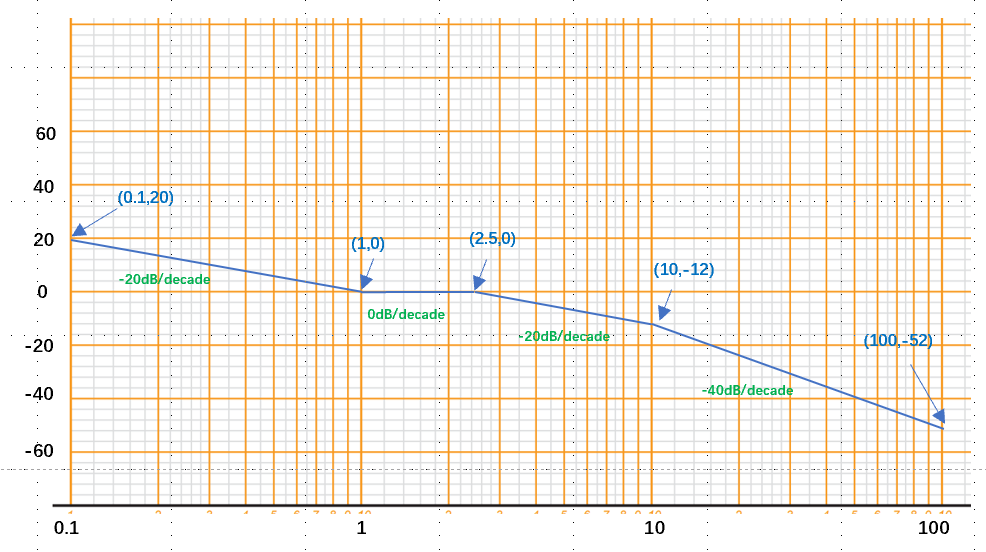
真实的波特图可以通过MATLAB中使用命令bode()得到,下图展示了\(G(s)=\frac{s+1}{s(0.1s+1)(0.4s+1)}\)的幅值波特图。
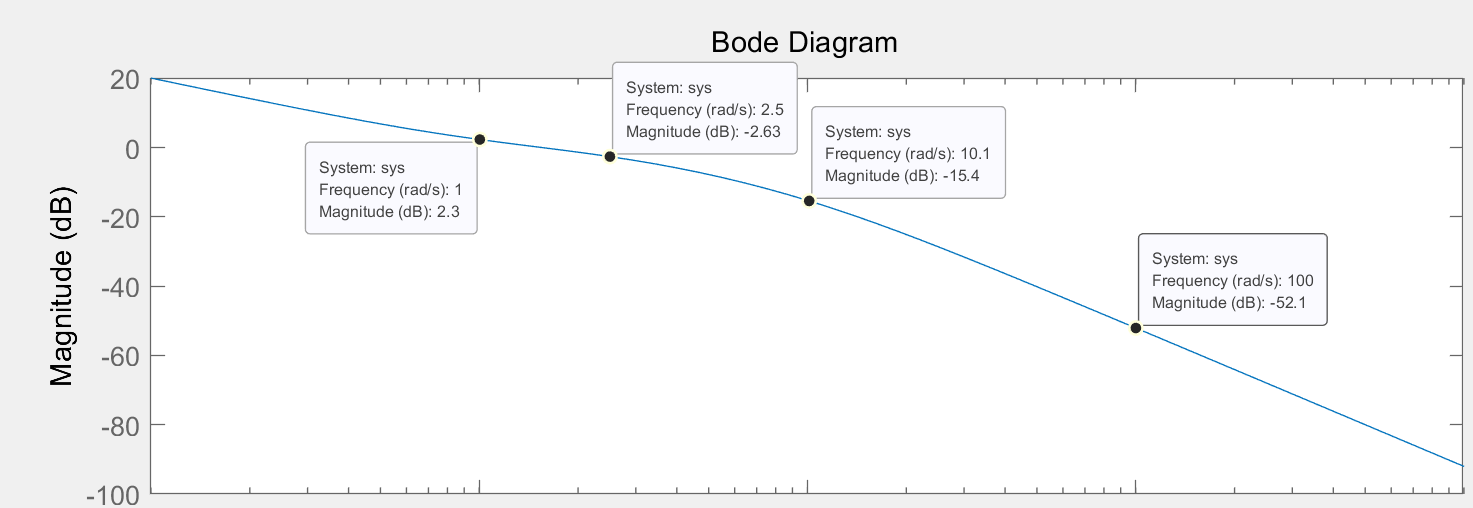
波特图特征
穿越频率
定义相位穿越频率(Phase crossover frequency)为相位波特图在-180°时对应的最小频率\(ω_{pc}\)。
增益穿越频率(Gain crossover frequency)为幅值波特图在0dB时对应的最小频率\(ω_{gc}\)。
增益裕量和相位裕量
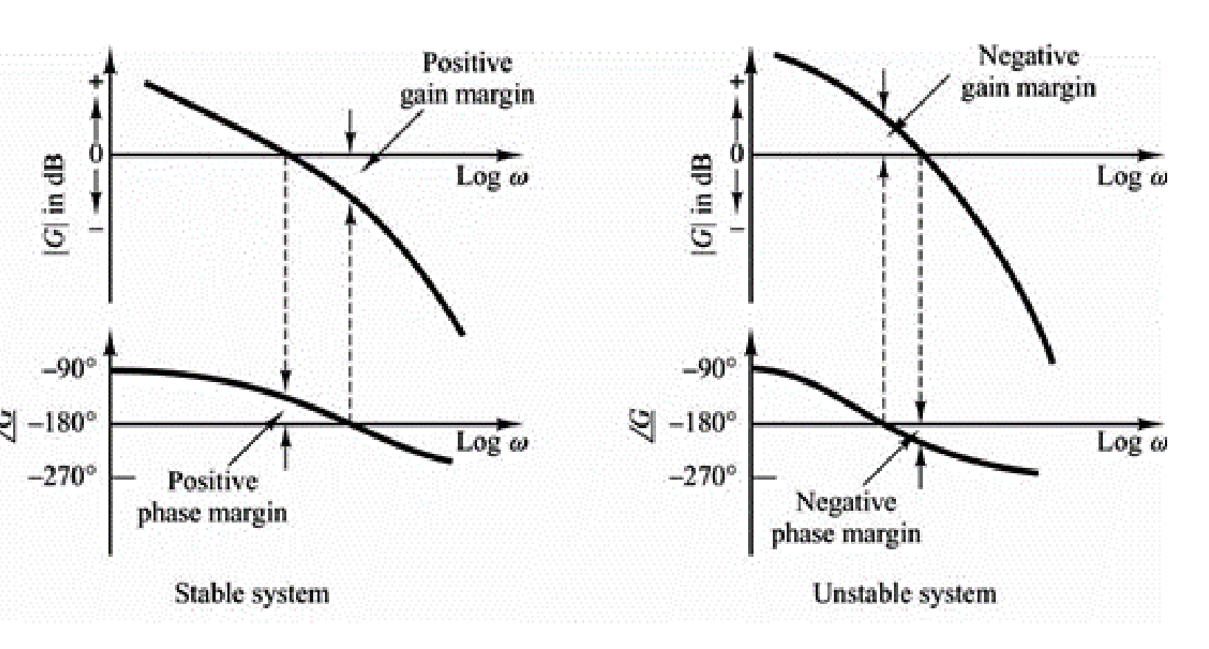
在波特图上,
增益裕量是0dB与相位穿越频率对应的幅值之差:
\[GM|_{dB}=0-|H(jω_{pc})|\] 相位裕量是增益穿越频率对应的相位与-180°之差:
\[PM=∠H(jω_{gc})-(-180°)\] 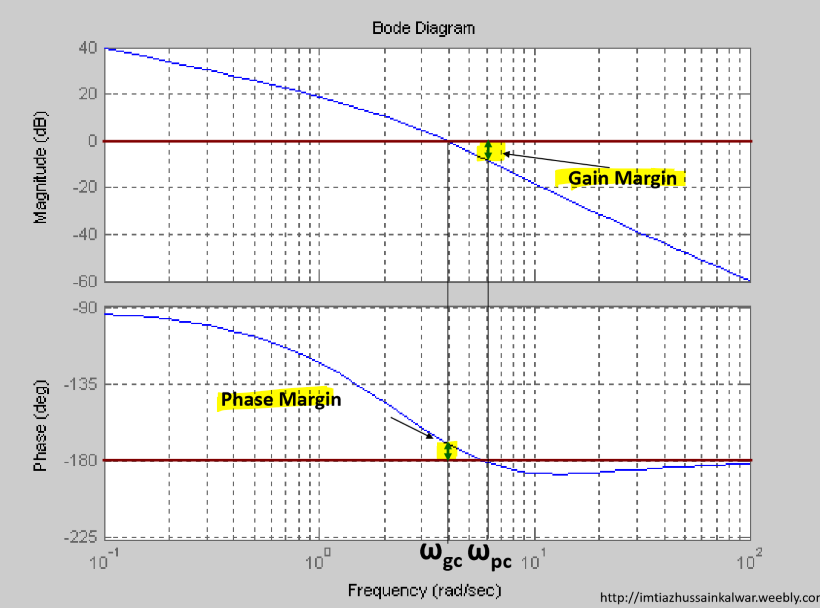
增益裕量和相位裕量与稳定性
如果相位裕量和增益裕量都大于0,则系统稳定。
如果相位裕量和增益裕量都为0,则系统处于临界稳定。
如果相位裕量和增益裕量中有一个小于零,则系统不稳定。
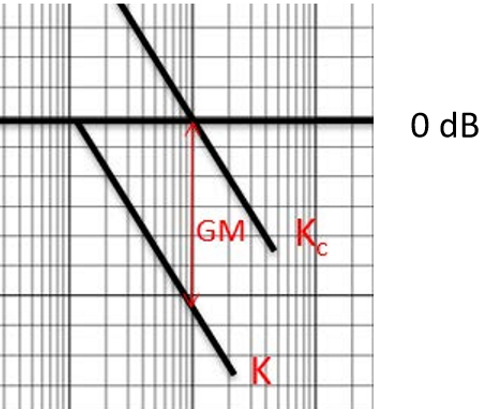
系统处于临界稳定时导致系统临界的增益部分\(K_c\)可以由如下公式给出:
\[GM=20lg\frac{K_c}{K}\] 其中\(K\)为系统增益。
从波特图反推开环传递函数
阻尼和固有频率
当相位裕量小于60°时,相位裕量、阻尼、带宽之间有如下关系:
\[PM=100°ζ\] \[\frac{B}{ω_n}=1-0.5ζ\] 其中\(B\)是系统带宽,是幅值为-3dB对应的频率。
可以通过波特图找出相位裕量和带宽,以此求得二阶系统的阻尼和固有频率。
初始值与系统类型
系统类型与其波特图关系如下所示:
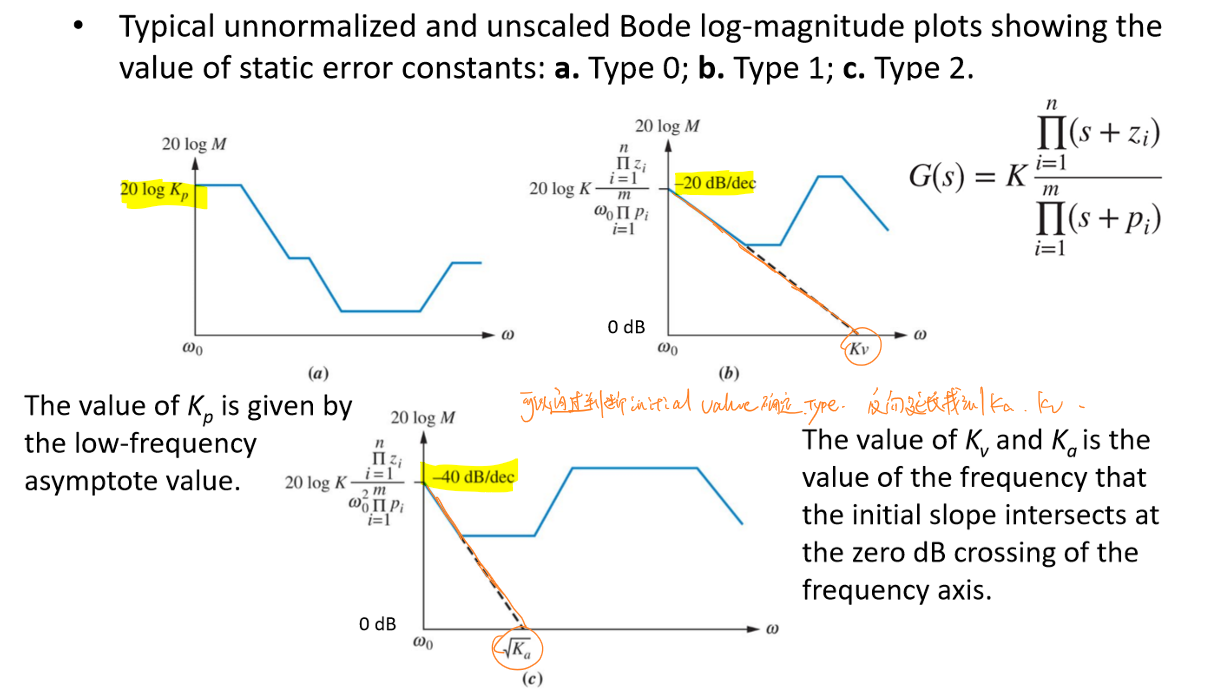
可以发现,通过初始值即可确定系统类型,即分母中\(s^N\)项的次数。0型系统的初始值为\(20lgK_p\),I型系统的初始值为-20dB,II型系统的初始值为-40dB。
终段斜率与系统阶数
系统波特图的最后一段斜率与系统阶数关系为:
\[k=-20O\]
零极点推断
系统增益
系统增益满足:
\[α=20lgK±20N_0lgω_0\] 其中\(ω_0\)为初始频率,\(α\)为初始频率对应的幅值。
积分和微分环节
可以根据初始斜率判断积分/微分环节\(s\)的存在:
初始斜率为\(±20N_0\),如果初始斜率为正,则代表系统存在\(N_0\)个积分环节,如果初始斜率为负,则代表系统存在\(N_0\)个微分环节。
一阶和二阶项结构
根据之前的讨论可以知道:
- 系统波特图上的转折点对应频率为系统的零点或者极点
- 波特图上发生斜率变化一定由加入的零点/极点极点造成:一阶项对初始斜率的贡献为\(20dB\),二阶项对斜率的贡献为\(40dB\)。如果元素位于分母(极点),则斜率贡献为负,如果元素位于分子(零点),则斜率贡献为正。
根据这两条理论则可以判断每一个区间上影响其斜率变化的极点/零点结构类型。
如果存在修正,可以根据在固有频率处修正前后的幅值差求得\(ζ\):
\[M_c=20lg(2ζ)\]
控制系统的电路实现
根据波特图的理论分析,任何一个系统的传递函数都可以表示为前文提到的元素组成,这些元素的电路图如下表所示:
| 名称 | 传递函数 | 电路图 |
|---|---|---|
| 比例环节 | \(G(s)=\frac{R_2}{R_1}=K\) | 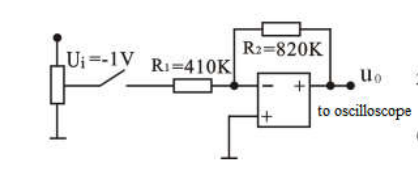 |
| 惯性环节 | \(G(s)=\frac{R_2}{R_1}\frac{1}{R_2Cs+1}=\frac{K}{Ts+1}\) | 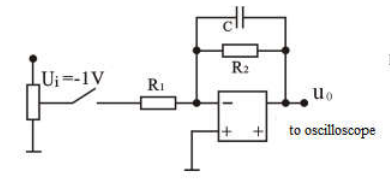 |
| 积分环节 | \(G(s)=\frac{1}{R_1Cs}=\frac{1}{Ts}\) | 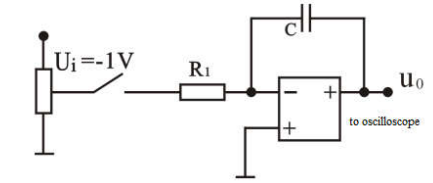 |
| 振荡环节 | \(G(s)=\frac{\frac{K}{T_1}}{s^2+\frac{s}{T_1}+\frac{K}{T_1}}\) \(K=\frac{R_2}{R_1},T_1=R_2C_1\) |
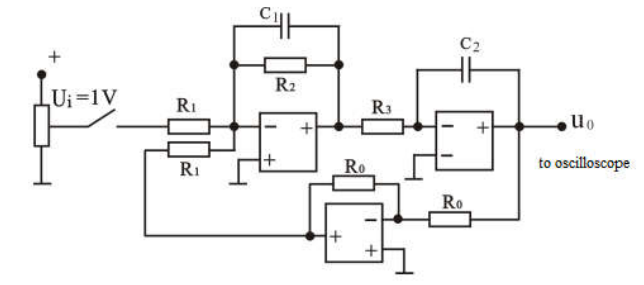 |
更多有关控制系统电路实现的内容请参考专为本专业、本课程设计的实验用具:THKKL-1 Control Theory Experimental Box,浙江天煌教仪的实验指导书:点此链接下载