06. 时延·非最小相位·系统近似方法

时延·非最小相位·系统近似方法

时延的影响

时延(Time-delay)指系统输入到对该输出进行响应之间的一段时间，在s域中长度为\(T\)时间的时延表示为：\(e^{-sT}\)。
由\(s=jω\)，系统\(G(jω)\)时移后的结果为：
\[G'(jω)=|G(jω)|e^{j∠G(jω)}e^{-jωT}=|G(jω)|e^{j∠[G(jω)-ωT]}\] 可以发现，时延对系统的幅频响应没有影响，而使相频响应下降\(-ωT\)。
因此，此时的相位裕度应该为：
\[PM_{delay}=PM-ω_{gc}T\]

对系统稳定性的影响

下图展示了\(TF(s)=\frac{5}{s+5}\)在不同时延下的奈奎斯特图：

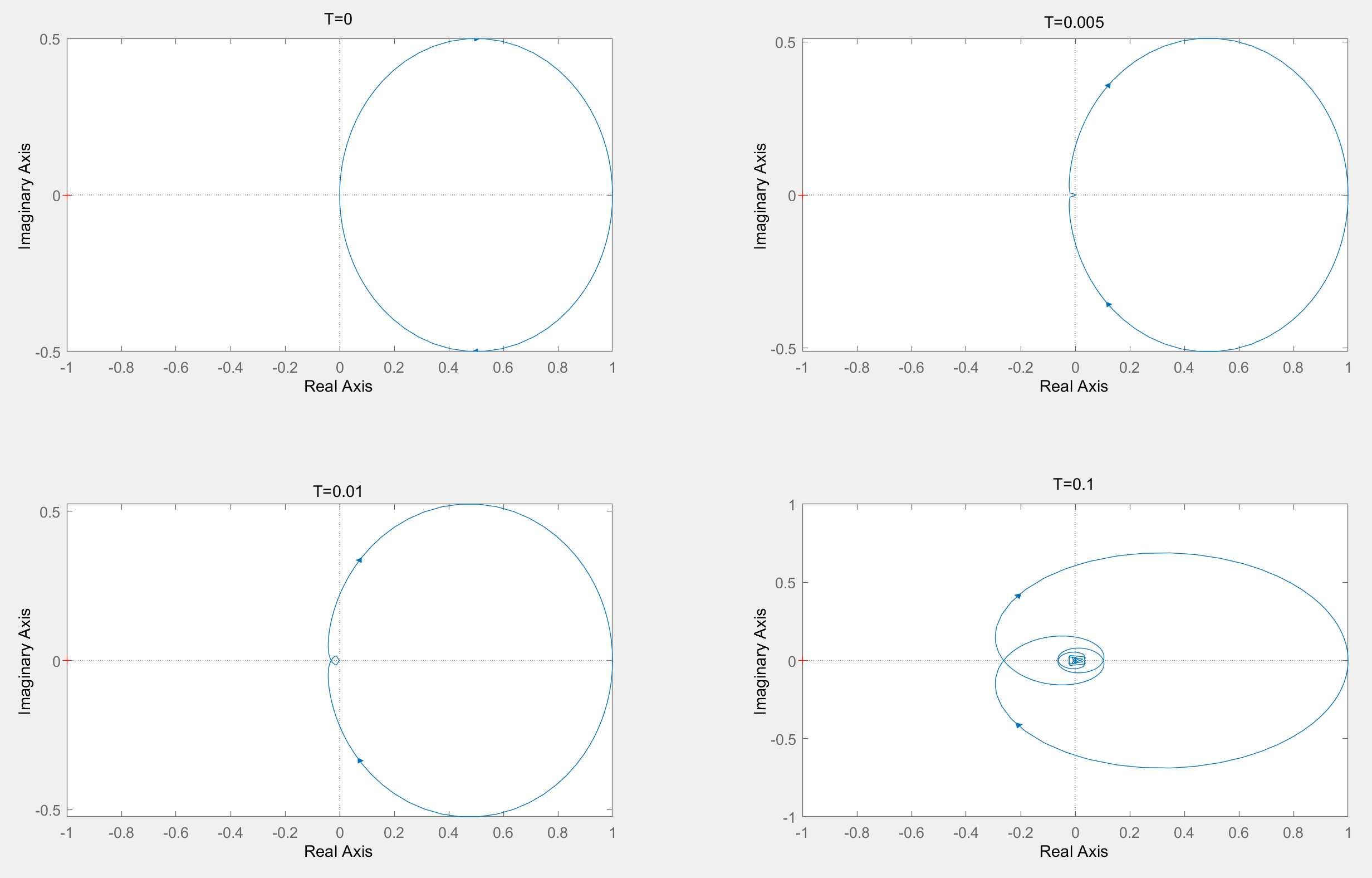
可以发现，加入时延之后，系统的奈奎斯特图会在实轴交点处出现更多的对数螺旋曲线。
此时规定，以第一过零点来判断系统的幅值裕度。

对阶跃响应的影响

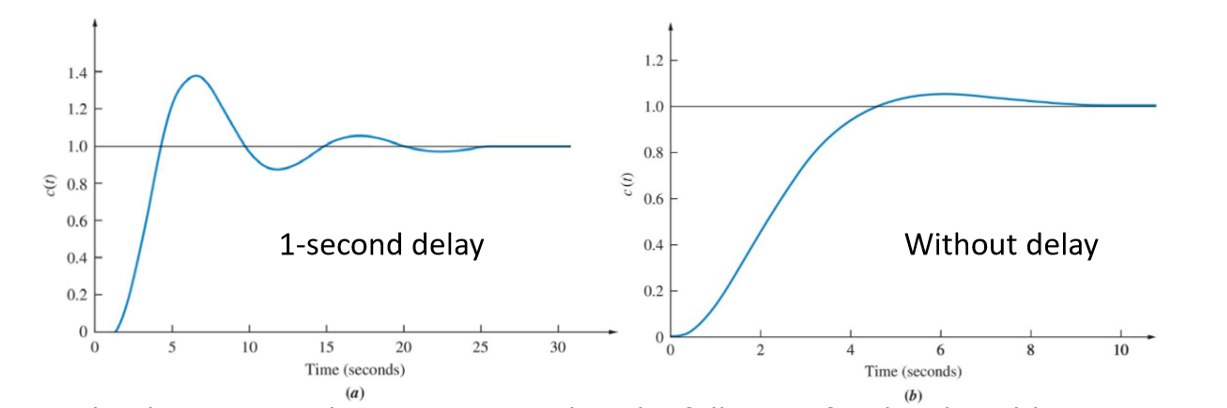
加入时延之后，系统的阻尼比减小，阶跃响应的图像的振荡更加剧烈。

非最小相位系统

真分传递函数（exactly proper transfer function/proper transfer function）指传递函数分子多项式的次数不超过分母多项式的次数。若分子的次数小于分母的次数，则称为严格真分传递函数（strictly proper transfer function）。
当系统的传递函数稳定，且在s域右半平面存在零点时，称系统是非最小相位系统。最小相位系统在波特图上高频稳定区域的相位角应当为\(-90°r\)，其中\(r\)是传递函数分子分母最高次数的差值。非最小相位系统在高频的相位角不存在如上的关系。
非最小相位的出现不能够保证“初始下冲”，“过冲”和过零的出现。

初始下冲

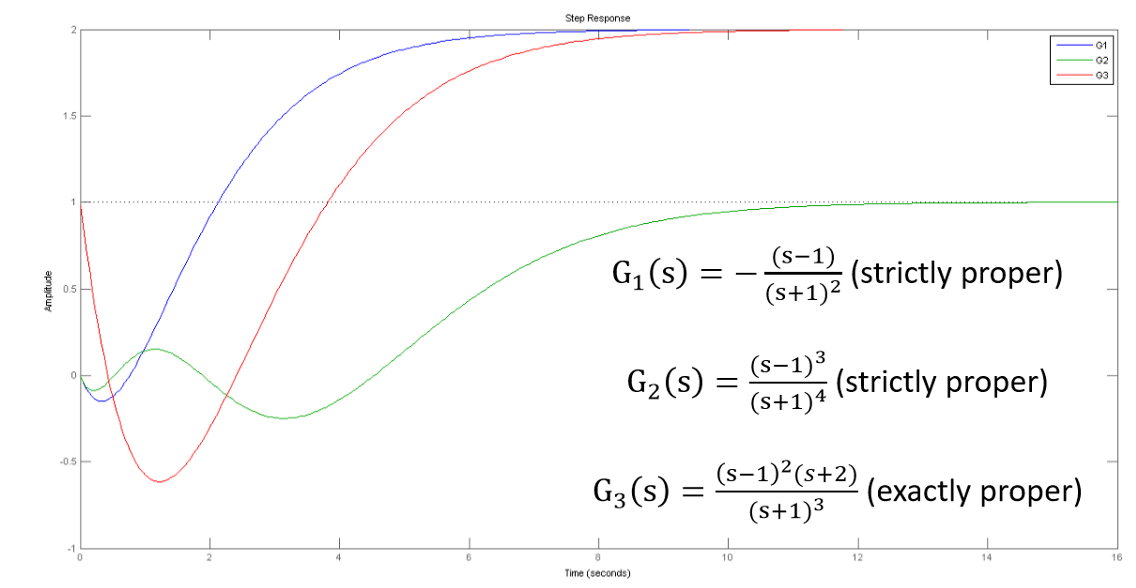
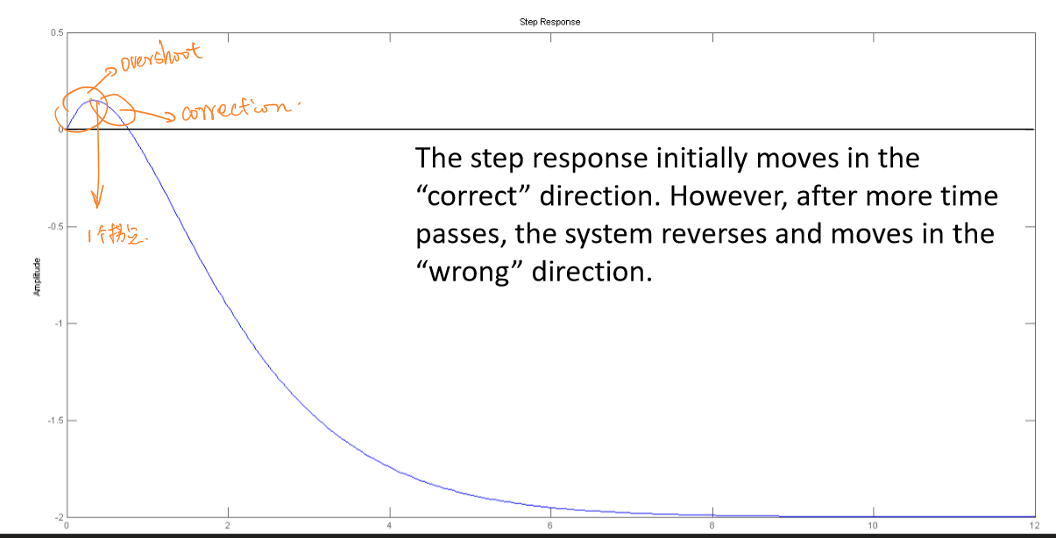
初始下冲（initial undershoot）指在初始点偏离阶跃响应最终的渐近方向。
如果真分传递函数\(G(s)\)中存在奇数个正零点，或者严格真分传递函数\(G(s)\)的\(G(s)-G(∞)\)存在奇数个正零点那么对应的系统会出现初始下冲。如果系统是非最小相位的，则不能保证出现初始下冲。

过零次数

如果真分传递函数\(G(s)\)中存在奇数个正零点，其正零点的个数对应拐点的个数，也是其阶跃响应过零(crossing zero)的次数。

过零次数不包括点(0,0)。

如果严格真分传递函数\(G(s)\)的\(G(s)-G(∞)\)存在奇数个正零点，其正零点的个数对应拐点的个数，也是\(G(s)\)阶跃响应过零(crossing zero)的次数。
如果系统是非最小相位的，则不能保证其过零次数一定为正零点个数。

高阶系统近似方法

主极点近似

通过对每个极点对整个系统的贡献时间长短分析，可以发现s域左半平面越接近虚轴的极点对系统影响的持续时间最长，称系统中s域左半平面最接近虚轴的极点为主极点（dominant pole）。主极点近似则是使用主极点对应的子系统传输函数以拟合整个系统的传输函数。
对于一阶项组成的系统，有：
\[[H(s)=\frac{K}{(s+a)(s+b)}]≈[H_{dp}(s)=\frac{K_{dp}}{s+a}]\] 其中\(a\)是主极点，且满足：
\[H(0)=H_{dp}(0)\] 利用上述式子可以求得\(K_{dp}\)。
对于含有二阶项的系统，则将共轭复根的实部\(ζω_0\)与其他极点进行比较，有：
\[[H(s)=\frac{aω^2_n}{(s+a)(s^2+2ζω_ns+ω_n^2)}]≈\begin{cases} &\frac{a}{s+a},a<<ζω_0\\ &\frac{ω^2_n}{s^2+2ζω_ns+ω_n^2},α>>ζω_0\\ \end{cases} \] 主极点近似的局限性为，如果子系统有相同的极点（即含有\((s+a)^N\)），则由于无法确定主极点而无法使用主极点近似。

零极点对消

当系统的零点和极点非常接近时，可以直接视为相同项而进行分子分母化简。例如：
\[H(s)=\frac{s+å}{(s+a)(s+b)}≈\frac{1}{s+b},å≈a\]