07. PID 控制系统

PID 控制系统

基本PID控制元件

控制器是在控制系统中用于控制系统误差的一种元件，其输入信号为系统误差。PID控制器是控制系统中最常用的控制器类型，基本的控制器有P控制器、I控制器、D控制器三种。这个控制器把收集到的数据和一个参考值进行比较，然后把这个差别用于计算新的输入值，这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。PID控制器可以根据历史数据和差别的出现率来调整输入值，使系统更加准确而稳定。PID控制器的比例单元（P）、积分单元（I）和微分单元（D）分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性，一般认为PID控制器是最适用的控制器。藉由调整PID控制器的三个参数，可以调整控制系统，设法满足设计需求。控制器的响应可以用控制器对误差的反应快慢、控制器过冲的程度及系统震荡的程度来表示。

P 控制器/比例控制器

P控制器，又称比例控制器（Proportional controller），其传输函数为：
\[D_c(s)=K_P\] \(K_p\)称为比例增益。
P控制器的系统输出与输入的系统误差\(e\)成比例：
\[y(t)=K_Pe\]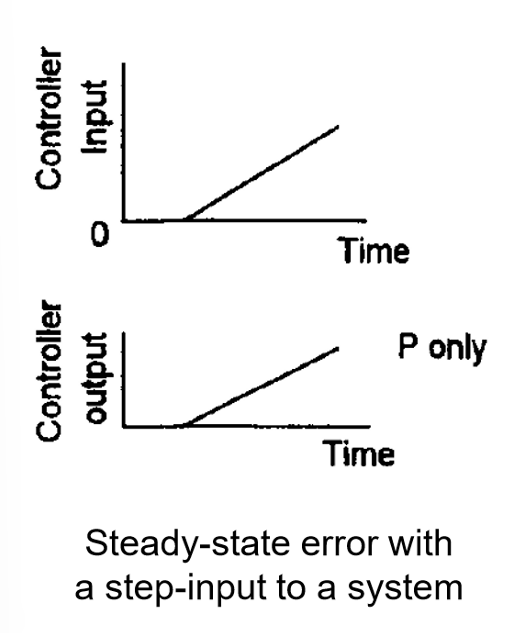

P控制器可以降低上升时间\(t_r\)，但是无法消去稳态误差。

I 控制器/积分控制器

I控制器，又称积分控制器(Intergral controller)，传输函数为：
\[D_c(s)=\frac{K_I}{s}\] \(K_I\)称为积分增益。
P控制器的系统输出与输入的系统误差\(e\)的积分成比例：
\[y(t)=K_I∫edt\]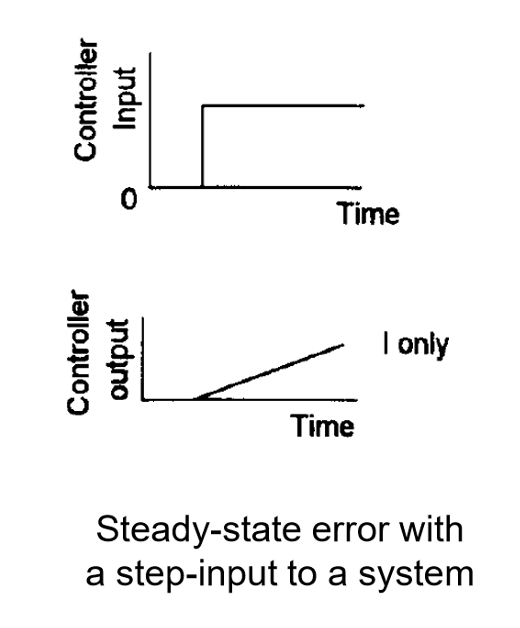

I控制器可以通过增加一个极点\(s=0\)来消去稳态误差，但是会增加系统的类型，使得系统的稳定性降低、瞬态响应变化更加剧烈。

D 控制器/微分控制器

D控制器，又称微分控制器(Derivative controller)，传输函数为：
\[D_c(s)=K_Ds\] \(K_I\)称为积分增益。
P控制器的系统输出与输入的系统误差\(e\)的微分成比例：
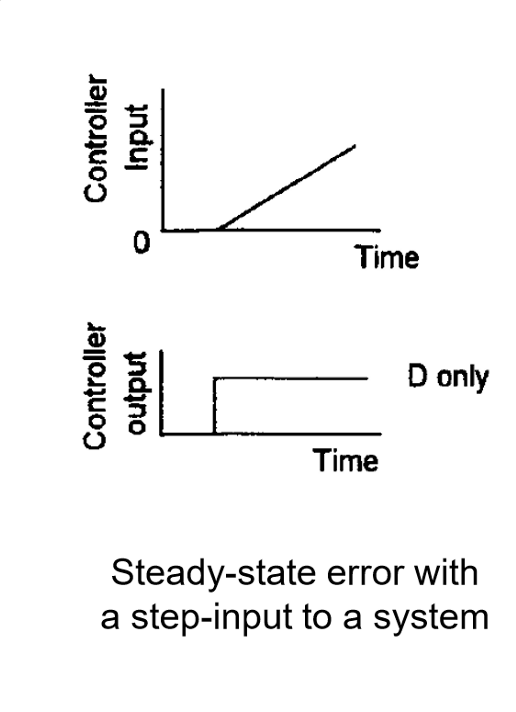
\[y(t)=K_D \frac{d}{dt}e\]

D控制器通过增加一个零点来改进系统稳定性、并使得瞬态响应变化更平稳、过冲率降低，但是会放大高频噪声。由于稳态误差信号为常数信号，斜率为0，因此D控制器对稳态误差信号没有响应。

组合控制器

由于P/D/I控制器单独使用都有缺陷，因此在工程设计上常常将其组合使用。

PI 控制器

PI控制器相比于I控制器能够在零频上对增益进行补偿，因此可以减小稳态误差。
PI控制器的传递函数为：
\[D_c(s)=\frac{K}{s}(s+\frac{1}{T_1})=K+\frac{K}{T_1s}\]

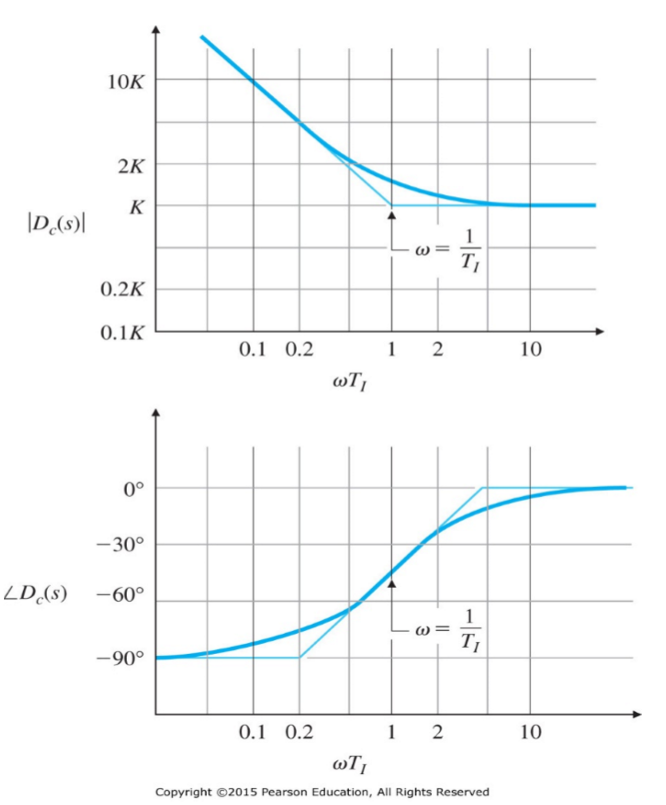
通过其波特图可以发现：PI控制器通过减少系统在高频部分的增益来减少相位裕量，同时系统的高频分量常常是噪声，因此PI控制器也可以起到限制噪声的作用。
同时，由于\(\lim_{s→∞}D_c(s)=K\),PI控制器没有稳态误差(Offset)。

PD 控制器

由于D控制器对稳态误差没有响应，因此在使用时常常与P控制器连用以改进这一特性。
PD控制器的传递函数为：
\[D_c(s)=T_Ds+1\]

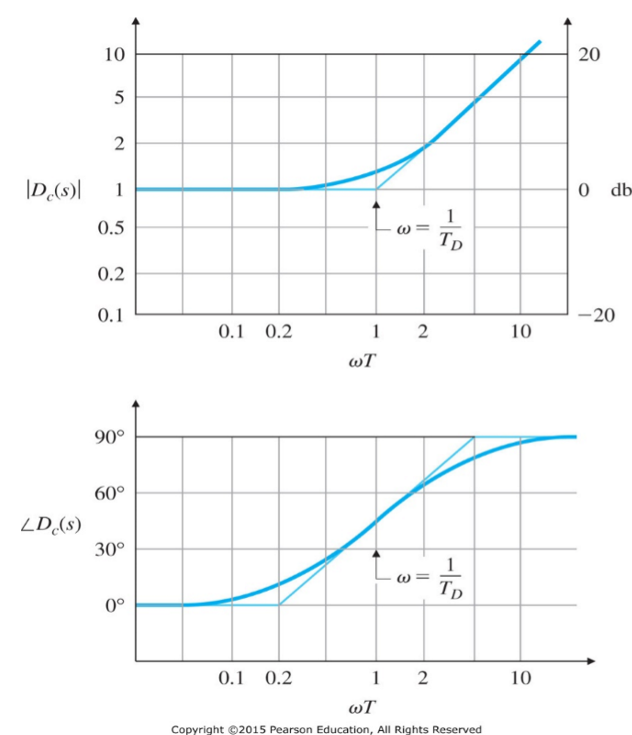
通过其波特图可以发现：PD控制器降低了系统在低频部分的增益，同时增加了在高频部分的增益，因此PD控制器增加了相位裕量。
但同时由于系统噪声常常位于高频，PD控制器也会放大系统的噪声。

PID 控制器

PID控制器能够减小系统响应的振荡，同时PID控制器自身不会有稳态误差。
PID控制器的传输函数为：
\[D_c(s)=K_P+\frac{K_I}{s}+K_Ds···\text{并联形式}\] \[D_c(s)=K_P(1+\frac{1}{T_is}+T_ds)···\text{标准形式}\] 其中，\(T_i=\frac{K_P}{K_I}\)，\(T_d=\frac{K_D}{K_P}\)

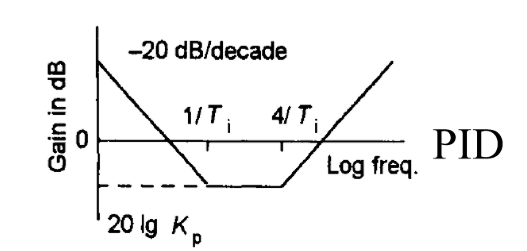
PID控制器的波特图形状取决于\(T_i\)和\(T_d\)的值，通常取\(T_i=4T_d\)：

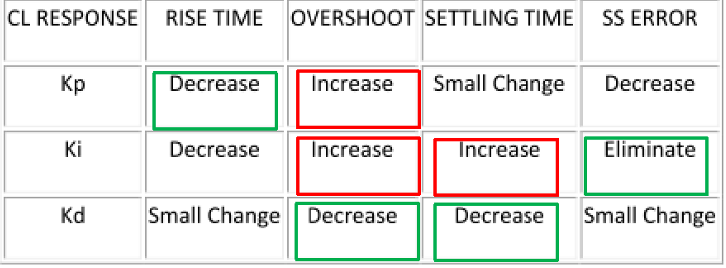
下图展示了PID控制器中参数调节对其阶跃响应的影响。

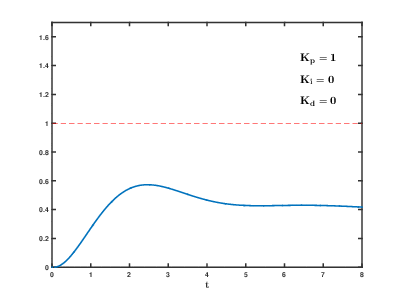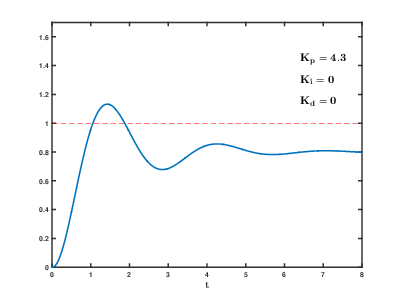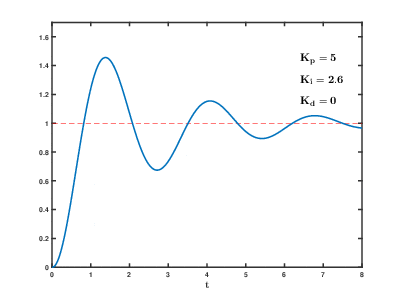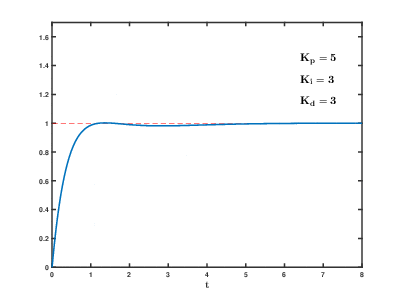
PID控制器的调节方法

通过实验对PID控制器进行调整的方法称为齐格勒－尼科尔斯方法(Ziegler-Nichols method)，其方法包括两种调节方式：
- 阶跃响应法 - 频率响应法

阶跃响应法

阶跃响应法（Step response method）适用对象是系统的阶跃响应呈现“s”形状的曲线，如下图所示：

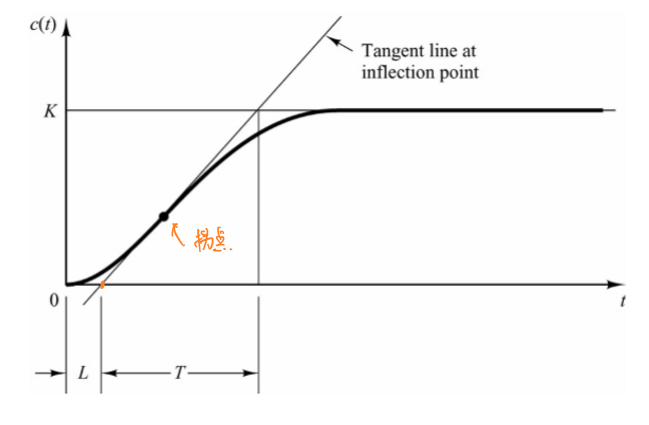
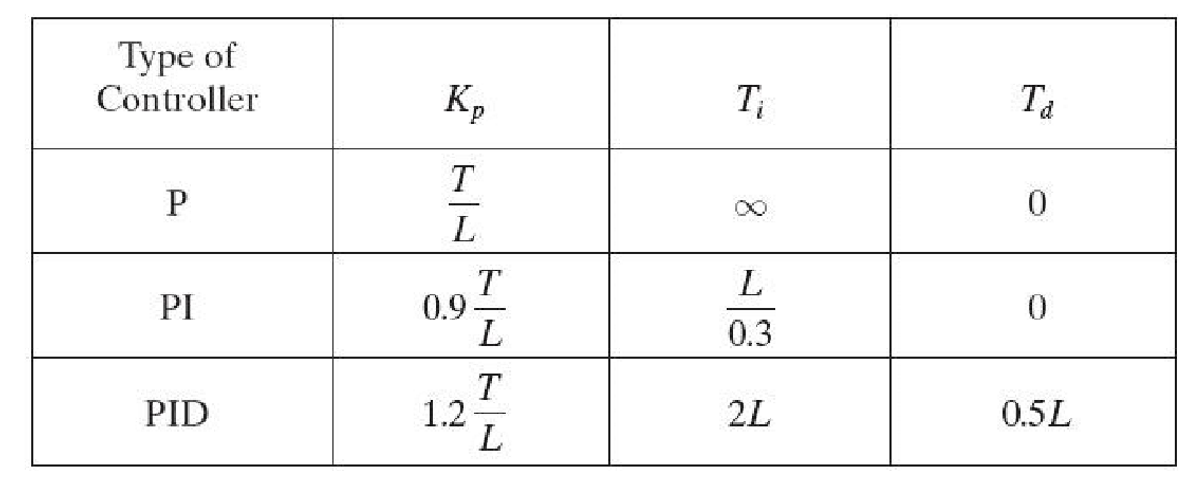
这个曲线可以描述为：
\[\frac{C(s)}{U(s)}=\frac{Ke^{-Ls}}{Ts+1}\] 其中曲线拐点（曲线二阶导为0的点）对应的切线与\(x\)轴的交点将\(x\)轴分为两部分：\(L\)和\(T\)，其中\(T\)是拐点处的切线与\(c(t)=K\)（即渐近线/最大值）的交点所对应的\(x\)轴坐标到切线与\(x\)轴的交点的距离；\(L\)是切线与\(x\)轴的交点到坐标原点的距离。
根据曲线可以得到\(K\)、\(L\)、\(T\)三个常数，并依据如下的表格进行PID控制器的设计：

频率响应法

频率响应法（Frequncy response method）适用于需要改进的系统（plant）在s域原点存在零点。
频率响应法的步骤是： - 首先应用P控制器改进开环传递函数，改进后系统的闭环传递函数为：
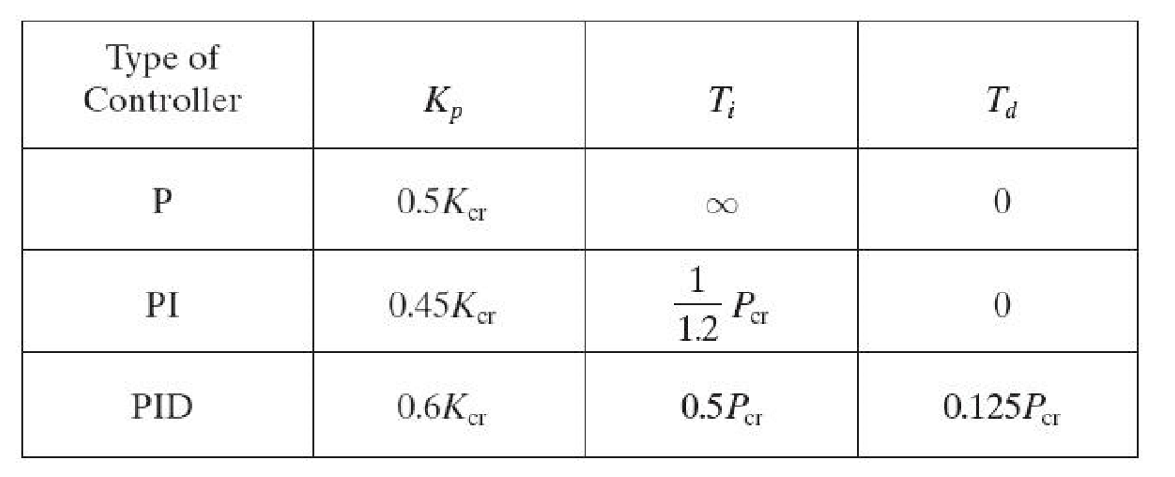
\[\frac{C(s)}{R(s)}=\frac{K_P+∏(s+z_i)}{K_P+∏(s+p_i)}\] - 将\(K_P\)的值增加，直到系统达到临界稳定条件，得到此时的\(K_P=K_{cr}\)。
或者应用劳斯判据求出劳斯表第一列每一项等于0时最小的\(K_P\)得到此时的\(K_P=K_{cr}\)。 - 根据系统闭环传递函数的特征方程，求得方程\(K=K_{cr}\)时的解，对应角频率\(ω_{cr}\)，根据\(P_{cr}=\frac{2π}{ω_{cr}}\)找到系统临界稳定时系统阶跃响应的振荡周期\(P_{cr}\)。
- 根据下表得到PID控制器的参数并设计。

在MATLAB中可以使用PID Tuner应用，选择“import new plant”导入使用tf()命令生成的系统传递函数，选择“show parameter”展示当前PID控制器的参数，并对其进行调制，直到满足设计要求。

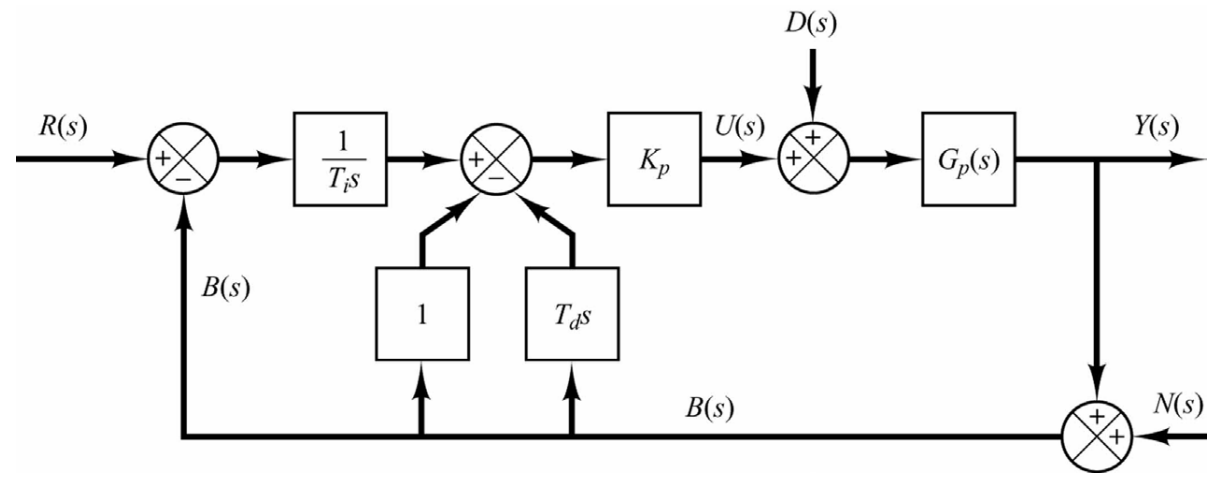
PID控制器的改进

对于常规的PID系统（如下图所示），如果输入信号\(R(s)\)为阶跃函数时，由于控制中出现的微分项\(T_ds\)，控制模块的输出：操纵变量中会含有冲激函数（\(\frac{d}{dt}u(t)=δ(t)\)）。

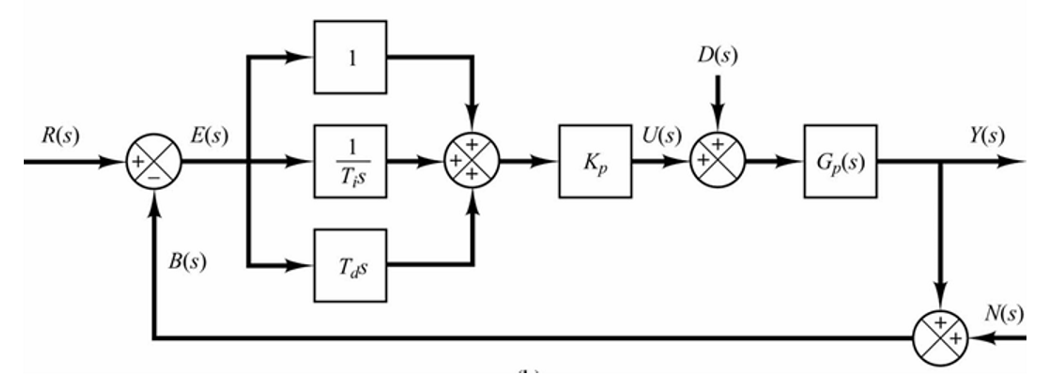
为了解决这一办法，通常应用常规PID系统时，会对微分项进行修正：
\[T_ds⇒\frac{T_ds}{1+γT_ds},γ≈0.1\] 这样的修正虽然可以保证操纵变量中没有冲激函数，但是操纵变量中仍然会存在一个多余的脉冲函数（这种现象称为set-point kick）。

PI-D控制器和I-PD控制器

一种改进的方法是将微分模块放置在系统的反馈部分，这样使得前馈信号不会受到影响。

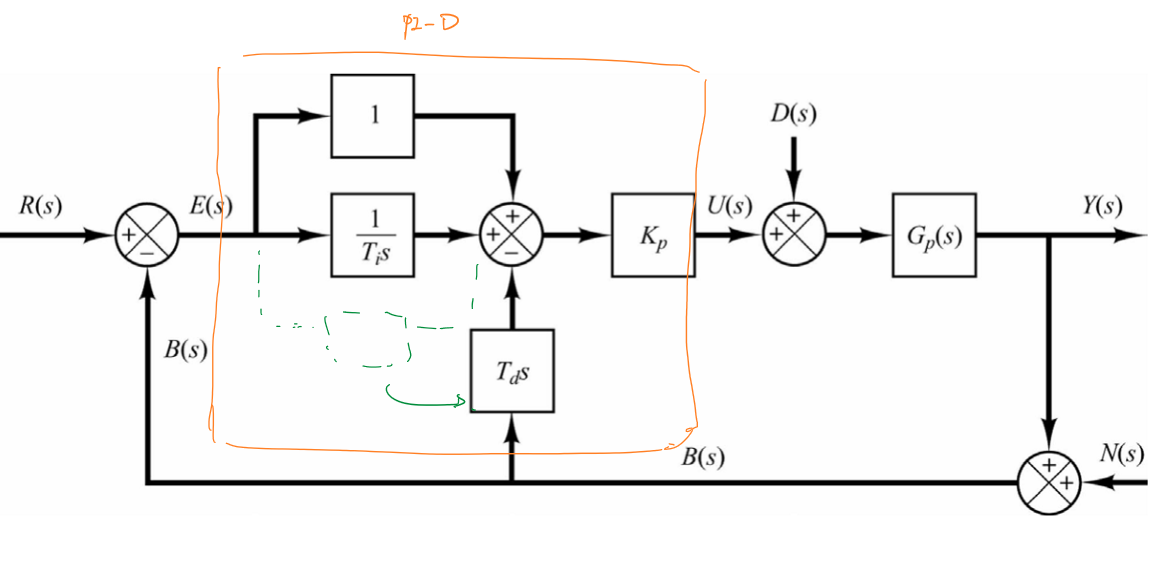
此外由于D控制器无法对稳态误差进行响应，因此可以将比例模块和微分模块同时设置在系统的反馈部分，称为I-PD控制器。

系统自由度

单自由度系统及设计

标准的PID系统中，其三个输入：系统输入\(R(s)\)、反馈噪声\(N(s)\)和干扰\(D(s)\)的闭环传递函数可以知一推三，称为单自由度PID控制系统。

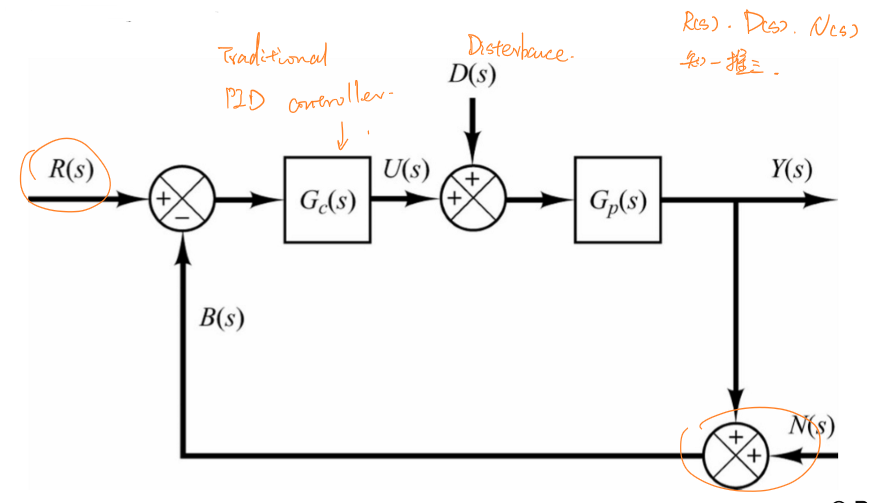
从上图中可以得出：
\[G_{yr}=\frac{Y(s)}{R(s)}=\frac{G_cG_p}{1+G_cG_p}\] \[G_{yd}=\frac{Y(s)}{D(s)}=\frac{G_p}{1+G_cG_p}\] \[G_{yn}=\frac{Y(s)}{N(s)}=-\frac{G_cG_p}{1+G_cG_p}\]

可以得到：
\[G_{yr}=\frac{G_p-G_{yd}}{G_p}\] \[G_{yn}=\frac{G_{yd}-G_p}{G_p}\] PID控制系统的传递函数又可以写作如下形式：
\[G_c(s)=\frac{K(as+1)(bs+1)}{s}\]

对如图所示的系统，如果\(G(s)\)为二阶，且假设整个系统的闭环传递函数的极点多项式为\((s+p_0)(s^2+2ζω_ns+ω_n)\)，可以发现极点为三部分组成：其中两个极点共轭:\(s=a±jb\)，另一个极点为实数，且通常取\(p_0=5ζω_n\)使得实极点对系统响应的影响较小。
可以根据系统设计的要求得到\(ζ\)和\(ω_n\)，并得到\((s+p_0)(s^2+2ζω_ns+ω_n)\)。通过展开这个多项式，应用待定系数法可以得到\(a,b,K\)的值。

去零法

对系统：
\[\frac{Y(s)}{R(s)}=\frac{p(s)}{s^{n+1}+a_ns^n+...+a_2s^2+a_1s+a_0}\] 如果将极点多项式\(p(s)\)设置为零点多项式的低次项，比如：
\[p(s)=a_2s^2+a_1s+a_0\] 如此，系统的阶跃、一阶(\(R(s)=s\))、二阶响应(\(R(s)=\frac{1}{2}s^2\))将会没有稳态误差，这种方法称为去零法（zero-placement approach）。

双自由度系统

整个系统的闭环传输函数中如果三个开环增益中的一个已知，则另外两个中一个已知，另一个未知，这样的系统称为双自由度系统，如下图所示：

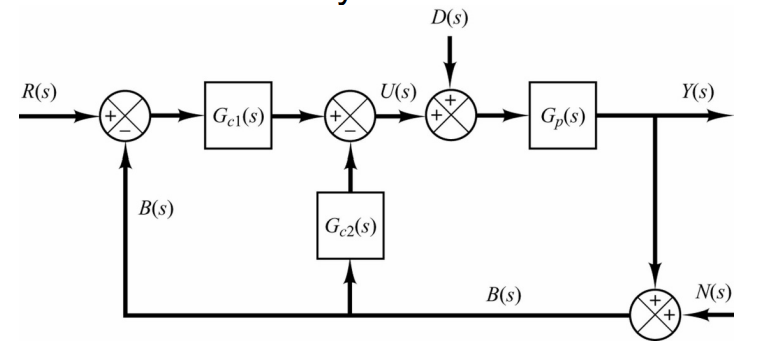
\[G_{yr}=\frac{Y(s)}{R(s)}=\frac{G_{c1}G_p}{1+(G_{c1}+G_{c2})G_p}\] \[G_{yd}=\frac{Y(s)}{D(s)}=\frac{G_p}{1+(G_{c1}+G_{c2})G_p}\] \[G_{yn}=\frac{Y(s)}{N(s)}=-\frac{(G_{c1}+G_{c2})G_p}{1+(G_{c1}+G_{c2})G_p}\] 可以推出：
\[G_{yr}=G_{c1}G_{yd}\] \[G_{yn}=\frac{G_{yd}-G_p}{G_p}\]

双自由度系统的优点

双自由度PID控制器可以解决常规PID控制器在实际应用中不兼容的问题。
双自由度系统有：
- 非常低的过冲
- 不容易受干扰影响
- 调节时间很短