08. 通过频率响应对PID控制系统进行改进

通过频率响应对PID控制系统进行改进

在使用频率响应对系统进行设计时，通过波特图可以得到系统的稳定性；通过增大相位裕度可以减小过冲比：通常在设计时，相位裕度在45°到315°之间；增加低频幅值响应可以减小系统的稳态误差。

增益调整

增益调整的方法是：
1. 选择一个合适的\(K\)值，画出系统的频率响应图。
2. 通过设计标准中的过冲率(\(M_p\))要求，应用如下的公式得到\(ζ\)和\(PM\)：
\[ζ=-\frac{ln(M_p)}{\sqrt{π^2+ln^2M_p}}\] \[PM=arctan\frac{2ζ}{\sqrt{-2ζ^2+\sqrt{1+4ζ^4}}}\] 3. 在波特图上找到设计标准中相位裕量所对应的频率\(ω_{PM}\)，并找到其对应的幅值响应，其对应的幅值响应\(-AB\)则是需要抬升的幅值。
4. 对系统增益进行修正，有：
\[AB=20lg(\frac{K_{ad}}{K})\] 即可得到修正后的增益\(K_{ad}\)。

超前补偿和滞后补偿

在许多材料里会将PID控制器(PID controller)和补偿器(compansator)的概念混为一谈。事实上，补偿器使由若干个控制器组成的控制群(control group)，PID控制器可以算作是P控制器、I控制器、D控制器组成的补偿器。但是补偿器的组成不止有这几种控制器。因此，PID控制器是一种补偿器，但补偿器不一定是PID控制器。
另外，补偿器中的“补偿”一词更多指对于整个系统输出的补偿。而本节中的滞后补偿和超前补偿中的补偿更多地是指对PID控制器的补偿。

超前滞后补偿器是一种根据系统特性设计的补偿器，用于改善系统的频率响应特性。超前滞后补偿器可以与PID控制器结合起来，以改善系统的响应速度和稳定性。
在结合超前滞后补偿器和PID控制器时，可以将超前滞后补偿器放在PID控制器的前面或后面，具体取决于系统的需求和设计目标。以下是两种常见的结合方式:
- 前向串联结构
将超前滞后补偿器放在PD控制器的前面。这种结构可以通过增加超前滞后补偿器的超前部分来提高系统的相位裕量，并增加系统的频率响应速度。然后，PID控制器可以进一步调节系统的稳定性和抑制系统的振荡。

• 反馈串联结构
  将超前滞后补偿器放在PID控制器的后面。这种结构可以通过超前滞后补偿器来修正系统的频率响应特性，然后PID控制器可以根据反馈信号来调节系统的稳定性和精度。

在实际应用中，超前滞后补偿器的设计需要根据具体系统的特性进行调整和优化。可以使用系统辨识方法、频率响应分析等技术来确定超前滞后补偿器的参数，以及与PID控制器的结合方式。

超前补偿与pi控制区别

滞后补偿

对于PI控制器：\(G_c(s)=\frac{K(s+\frac{1}{T_i})}{s}\)，由于积分项\(\frac{1}{s}\)的出现导致PI控制器在加入系统后会改变系统原本的类型，进而改变已经调整好的系统动态响应（系统达到稳态前的响应）。因此，需要一种补偿使其能在\(s=0\)时提供非常大的开环增益，提高稳态误差常数，但是在高频区使得整个补偿后的系统增益保持为1，进而不会对系统的动态响应产生影响，这样的补偿称为滞后补偿(lag compansation)。
\[G_{lag}(s)=\frac{τs+1}{ατs+1},α>1\]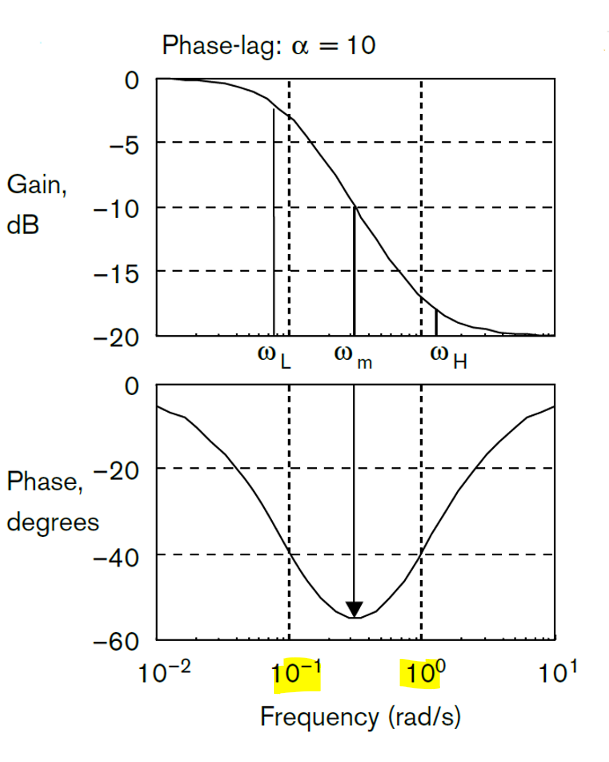

滞后补偿器设计

滞后补偿器设计的思路是利用补偿将现在系统的幅度响应在补偿器设计要求的相位裕量处调整到0dB。
- 利用稳态误差的定义，找到系统增益\(K\) - 绘制出\(KG(s)H(s)\)的波特图，从波特图上寻找系统的相位裕量\(PM\) - 在波特图上找到符合补偿器设计要求的相位裕量\(PM'+Φ\)（其中\(Φ\)是修正系数），找到对应的增益穿越频率\(ω'_{gc}\)。
- 找到\(ω'_{gc}\)对应的幅值\(K'\)，并计算： \[α=10^{\frac{K'}{20}}\] - 令: \[τ=\frac{10}{ω'_{gc}}\] - 带入\(α\)和\(τ\)，得到滞后补偿器的前向传输方程\(G_{lag}(s)\)。

添加滞后补偿器后，系统的前向传输方程/开环传递函数表示为：
\[KG_{lag}(s)G(s)H(s)\]

如果设计要求是阻尼比\(ζ\)，通常阻尼比可以通过如下公式近似为系统设计对相位裕量的要求：
\[PM(°)⩰100ζ\]

超前补偿

对PD控制器：\(G_c(s)=T_ds+1\)，其幅值随着频率的升高而线性升高，但是这种特性会放大高频噪声，使系统抗噪性下降。因此，需要一种补偿通过增加一个极点进而在高频处降低系统幅值，这样的补偿称为超前补偿(lead compansation)。
\[G_{lead}(s)=\frac{τs+1}{βτs+1},β<1\]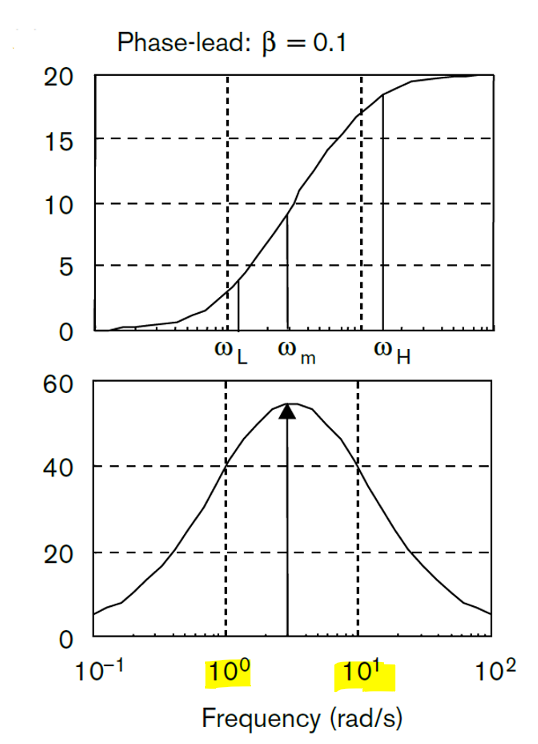

超前补偿器设计

超前补偿器的设计思路是将相位波特图在高频处的部分进行抬升，具体的设计步骤是：
- 利用稳态误差的定义，找到系统增益\(K\) - 绘制出\(KG(s)H(s)\)的波特图，从波特图上寻找系统的相位裕量\(PM\) - 通过公式：
\[φ_m=(PM'+φ_c)-PM\] 其中\(PM'\)是设计要求的相位裕量，\(Φ\)是修正系数。
计算出需要抬升的相位。
- 利用公式：
\[β=\frac{1-sinφ_m}{1+sinφ_m}\] 计算得到β。
- 在波特图上找到幅值为\(-10lg\frac{1}{β}\)对应的频率\(ω'_m\)，令: \[τ=\frac{1}{ω'_{m}\sqrt{β}}\] - 带入\(β\)和\(τ\)，得到超前补偿器的前向传输方程\(G_{lead}(s)\)。

添加滞后补偿器后，系统（称为补偿系统）的前向传输方程/开环传递函数表示为：
\[KG_{lead}(s)G(s)H(s)\]

在工程中，还需要绘制补偿系统的波特图以检验相位裕量和增益裕量以及稳态误差系数是否满足设计要求。
如果不满足，则应当降低\(β\)的值，重新计算\(τ\)并找到一组符合设计要求的参数。

超前-滞后补偿*

超前滞后补偿可以改善稳态误差，也可以加快系统达到稳定的速度。超前-滞后补偿的传递函数为：
\[G_{lag-lead}(s)=\frac{(τ_{lag}s+1)(τ_{lead}s+1)}{(ατ_{lag}s+1)(βτ_{lead}s+1)}\] 在设计时通常选取\(α=\frac{1}{β}\)，如此，在低频时补偿器增益将为0dB。
通常在设计时先通过设计要求找到\(α\)，并设计出滞后补偿器，再利用\(β=\frac{1}{α}\)设计出超前补偿器。

使用MATLAB设计超前/滞后补偿器

在MATLAB中，可以使用APP：Control System Designer（或者通过命令sisotool唤出）设计超前/滞后补偿器。