09. 连续系统的状态空间表示和分析
本文最后更新于 2025年6月4日 晚上
连续系统的状态空间表示和分析
现代复杂控制系统中往往包含多个输入和多个输出,系统的分析更加复杂。使用一些数学方法可以简化对这些系统的分析。这些数学方法建立在对系统状态(state)的理解上:系统的状态是指系统变量、输入信号和用于描述系统动态变化的方程的集合,系统状态可以理解为系统的记忆,\(t=t_0\)时的系统状态能够记忆系统在\(t<t_0\)时系统的全部输入和之前全部系统的状态。系统的状态可以提供对系统未来状态和系统输出的分析。
系统的状态空间表示
系统的响应可以用一系列的由状态变量(\(x_i\))和输入信号表示的一阶微分方程:
\[\dot{x_1}=a_{11}x_1+a_{12}x_2+...+a_{1n}x_n+b_{11}u_1+...b_{1m}u_m\] \[\dot{x_2}=a_{21}x_1+a_{22}x_2+...+a_{2n}x_n+b_{21}u_1+...b_{2m}u_m\] \[...\] \[\dot{x_n}=a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n+b_{n1}u_1+...b_{nm}u_m\] 其中\(\dot{x}=\frac{d}{dt}x\).
这些系数和变量都可以被矩阵化:
\[\frac{d}{dt}\begin{bmatrix}
x_1 \\ x_2 \\ ⋮ \\ x_n
\end{bmatrix}=\begin{bmatrix}
a_{11} & a_{12} & \dots &a_{1n}\\
a_{21} & a_{22} & \dots &a_{2n}\\
⋮ & &\dots & ⋮ \\
a_{n1} & a_{n2} & \dots &a_{nn}\\
\end{bmatrix}\begin{bmatrix}
x_1 \\ x_2 \\ ⋮ \\ x_n
\end{bmatrix}+\begin{bmatrix}
b_{11} & \dots & b_{1m} \\
⋮ & & ⋮ \\
b_{n1} & \dots & b_{nm}
\end{bmatrix}\begin{bmatrix}
u_1 \\ u_2 \\ ⋮ \\ u_m
\end{bmatrix}\] 上述矩阵化方程可以被简写为:
\[\vec{\dot{x}}=A\vec{x}+Bu\] \(A\)是系统原型的系数矩阵(plant coeffient matrix),\(B\)是控制矩阵(control matrix)。
这个微分方程称为系统的状态方程(state equation),对应传递函数的极点多项式。
其中,\(\vec{\dot{x}}\)可以表示视为前一个时刻系统的状态(微分表示时延),\(\vec{x}\)和\(u\)是当前系统的状态和输入。即当系统之前的状态和当前的输入已知时,当前的系统状态被确定下来。
同时,线性系统的输出也可以由系统状态和输入信号两部分组成:
\[y=C\vec{x}+Du\] \(C\)是系统的输出观测矩阵(output observation matrix),\(D\)是直接耦合矩阵(direct coupling matrix)。
这个微分方程称为系统的输出方程(output equation),对应传递函数的零点多项式。
这两个方程组共同作用,可以准确的描述一个系统。用系统的状态方程和输出方程来描述系统的表达方式称为系统的状态空间表示(state-space representation/state-variable representation)。
某个特定系统的状态空间表达不是唯一的。
根据这两个方程可以建立如下的系统框图:
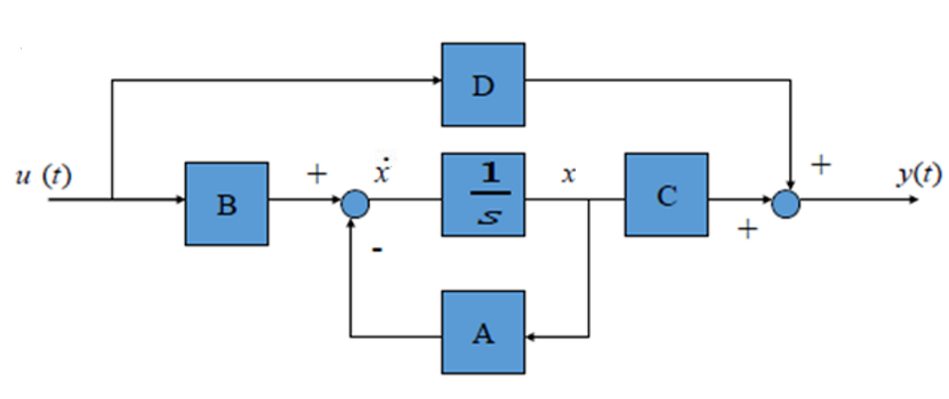
微分方程与状态空间的转换
对于一个\(n\)阶微分方程:
\[\frac{d^ny}{dt^n}+a_{n-1}\frac{d^{n-1}y}{dt^{n-1}}+...+a_0y=b_0u\] 可以将系统的输出变量及其微分形式视为系统的状态变量:
\[x_1=y\] \[x_2=\frac{dy}{dt}⇒\dot{x_1}=x_2\] \[...\] \[x_n=\frac{d^{n-1}y}{dt^{n-1}}⇒\dot{x_n}=\frac{d^ny}{dt^n}=-a_0x_1-a_1x_2-...-a_{n-1}x_n+b_0u\]
整理后就可以得到一系列的系统的状态方程:
\[x_1=y\] \[\dot{x_1}=x_2\] \[...\] \[\dot{x_n}=-a_0x_1-a_1x_2-...-a_{n-1}x_n+b_0u\] 将这些状态方程矩阵化即可得到系统的状态方程与输出方程:
\[\vec{\dot{x}}=A\vec{x}+Bu\] \[y=C\vec{x}+Du\]
信号流图与状态空间的转换
信号流图可以从一系列的系统状态方程得到:
- 画出系统的输入\(u\)或者\(r\),系统的每一个状态\(x_i\),以及系统输出\(y\)的节点。
- 根据每一个状态方程,将对应的节点用箭头连接,并标上对应的系数,注意用\(\frac{1}{s}\)表示微分。
下图表示了\(\begin{cases} \dot{x_1}=x_2\\ \dot{x_2}=x_3\\ \dot{x_3}=-24x_1-26x_2-9x_3+24r\\ y=x_1 \end{cases}\)的信号流图:
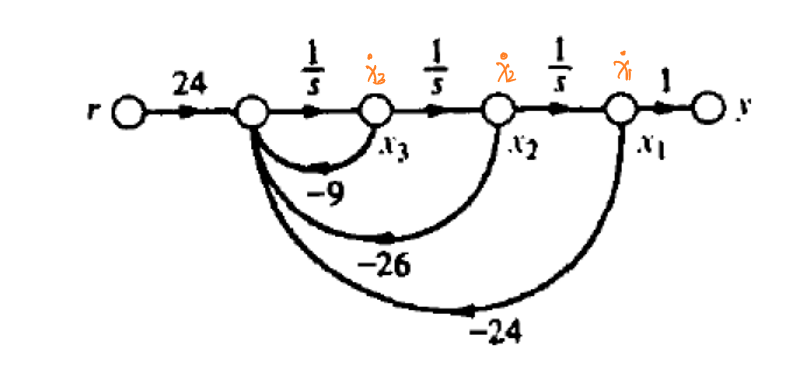
状态空间的表达形式(传递函数与状态空间的转换)
下面将介绍四种表达状态空间的形式,对于\(n\)阶微分方程:
\[\frac{d^ny}{dt^n}+a_{1}\frac{d^{n-1}y}{dt^{n-1}}+...+a_ny=\frac{d^nu}{dt^n}+b_{1}\frac{d^{n-1}u}{dt^{n-1}}+...+b_nu\] \(u\)表示系统输入,\(y\)表示系统输出。
那么在s域中有系统的传递函数:
\[\frac{Y(s)}{U(s)}=\frac{b_0s^n+b_1s^{n-1}+...+b_n}{s^n+a_1s^{n-1}+...+a_{n-1}s+a_n}\]
能控标准型
对于形如:
\[TF(s)=\frac{Y(s)}{U(s)}=\frac{b_0s^n+b_1s^{n-1}+...+b_n}{s^n+a_1s^{n-1}+...+a_{n-1}s+a_n}\] 的传递函数。
能控标准型(controllable-canonical form)的系数矩阵如下:
\[A=\begin{bmatrix}
-a_1 & -a_2 & ... & -a_{n-1} & -a_n \\
1 & 0 & ... & 0 & 0\\
0 & 1 & ... & 0 & 0\\
⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\
0 & 0 & ... & 1 & 0\\
\end{bmatrix}\] \[B=\begin{bmatrix}
1 \\ 0 \\ ⋮ \\ 0
\end{bmatrix}\] \[C=\begin{bmatrix}
b_1 & b_2 & b_3 &\dots&b_n
\end{bmatrix}\] \[D=[b_0]\] 能控标准型在系统所有状态都已知的情况下分析系统是很有用的。
相位变化型
对于形如:
\[TF(s)=\frac{Y(s)}{U(s)}=\frac{b_0s^n+b_1s^{n-1}+...+b_n}{s^n+a_1s^{n-1}+...+a_{n-1}s+a_n}\] 的传递函数。
相位变化型(phase-variable form)的系数矩阵如下:
\[A=\begin{bmatrix}
0 & 1 & ... & 0 & 0\\
⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\
0 & 0 & ... & 1 & 0\\
0 & 0 & ... & 0 & 1\\
-a_n & -a_{n-1} & ... & -a_{2} & -a_1 \\
\end{bmatrix}\] \[B= \begin{bmatrix}
0 \\ 0 \\ ⋮ \\ 1
\end{bmatrix}\] \[C=\begin{bmatrix}
b_n & b_{n-1} & b_{n-2} &\dots&b_1
\end{bmatrix}\] \[D=[b_0]\] 相位变化型矩阵在控制器设计中十分有用。
能观标准型
对于形如:
\[TF(s)=\frac{Y(s)}{U(s)}=\frac{b_0s^n+b_1s^{n-1}+...+b_n}{s^n+a_1s^{n-1}+...+a_{n-1}s+a_n}\] 的传递函数。
能观标准型(observable-canonical form)的系数矩阵如下:
\[A=\begin{bmatrix}
-a_1 & 1 & 0 &... & 0 & 0 \\
-a_2 & 0 & 1 &... & 0 & 0\\
-a_3 & 0 & 0 &... & 0 & 0\\
⋮ & ⋮ &⋮ &⋱ & ⋮ & ⋮ \\
-a_{n-1} & 0 & 0 &... & 0 & 1\\
-a_n & 0 & 0 &... & 0 & 0\\
\end{bmatrix}\] \[B=\begin{bmatrix}
b_1 \\ b_2 \\ b_3 \\ ⋮ \\ b_n
\end{bmatrix}\] \[C=\begin{bmatrix}
1 & 0 & 0 &\dots&0
\end{bmatrix}\] \[D=[b_0]\] 能观标准型在设计观测器时很有用。
对角标准型
对于形如:
\[\frac{Y(s)}{U(s)}=b_0+\frac{c_1}{s+p_1}+\frac{c_2}{s+p_2}+...+\frac{c_n}{s+p_n}\] 的传递函数。
在标准对角型(diagonal canonical form)下,状态矩阵\(A\)是一个对角矩阵,其对角线为其特征值,同时也是系统方程的极点。对角标准型只适用于系统没有重极点的情况。
\[A=\begin{bmatrix}
-p_1 & 0 & ... & 0 & 0\\
0 & -p_2 & ... & 0 & 0\\
⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\
0 & 0 & ... & 0 & -p_n\\
\end{bmatrix}\] \[B=\begin{bmatrix}
1 \\ 1 \\ ⋮ \\ 1
\end{bmatrix}\] \[C=\begin{bmatrix}
c_1 & c_2 & c_3 &\dots &c_n
\end{bmatrix}\] \[D=[b_0]\]
约旦标准型
当系统有重极点时,系统的状态空间表示可以用约旦标准型表示。当系统的传输函数为:
\[\frac{Y(s)}{U(s)}=\frac{b_0s^n+b_1s^{n-1}+...+b_n}{(s+p_1)^3(s+p_4)...(s+p_n)}\] 其中的状态矩阵是:
\[A=\left[\begin{matrix}
-p_1 & 1 & 0 &... & 0 & 0\\
0 & -p_1 & 1 &... & 0 & 0\\
0 & 0 & -p_1 &... & 0 & 0\\
⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\
0 & 0 & ... & 0 & -p_n\\
\end{matrix}\right]\] \[B=\left[ \begin{matrix}
0 \\ 0 \\ ⋮ \\ 1
\end{matrix}\right]\] \[C=[\begin{matrix}
c_1 & c_2 & c_3 &\dots &c_n
\end{matrix}]\] \[D=[b_0]\] 其中的\(c_i\)可以通过部分分式展开得到:
\[\frac{Y(s)}{U(s)}=b_0+\frac{c_1}{(s+p_1)^3}+\frac{c_1}{(s+p_1)^2}+\frac{c_1}{s+p_1}+\frac{c_2}{s+p_2}+...+\frac{c_n}{s+p_n}\]
状态空间表示与信号流图的转换
相位变化型
对传递函数\(\frac{Y(s)}{U(s)}\),可将其分解为:
\[\frac{Y(s)}{U(s)}=\frac{V(s)}{U(s)}\frac{Y(s)}{V(s)}=\frac{∑b_is^{(m-i)}}{∑a_is^{(n-i)}}\] 令\(x_1=v\)作为状态变量,对\(\frac{V(s)}{U(s)}\)可以得到一系列系统的状态方程。对\(\frac{Y(s)}{V(s)}\)可以得到系统的输出方程。
再根据状态方程和输出方程即可绘制信号流图。
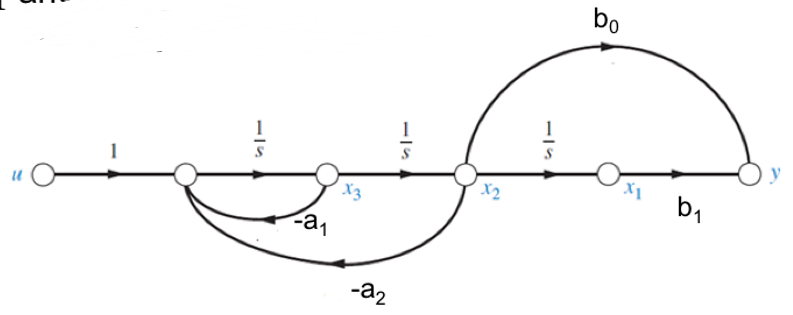
如果\(x_1,x_2,x_3\)的次序相反,那么得到的是能控标准型。
能观标准型
对系统的传递函数\(\frac{Y(s)}{U(s)}\),如果其写作如下的形式:
\[\frac{Y(s)}{U(s)}=\frac{b_0+b_1s^{-1}+...+b_ns^{-n}}{1+a_1s^{-1}+...+a_ns^{-n}}\] 则可以根据这个结构直接写出系统的状态方程和输出方程:
\[\dot{x_k}=-a_kx_1+x_{k+1}+b+ku,1≤k≤n-1\] \[\dot{x_n}=-a_nx_1+b_nu\] \[y=x_1+b+0u\]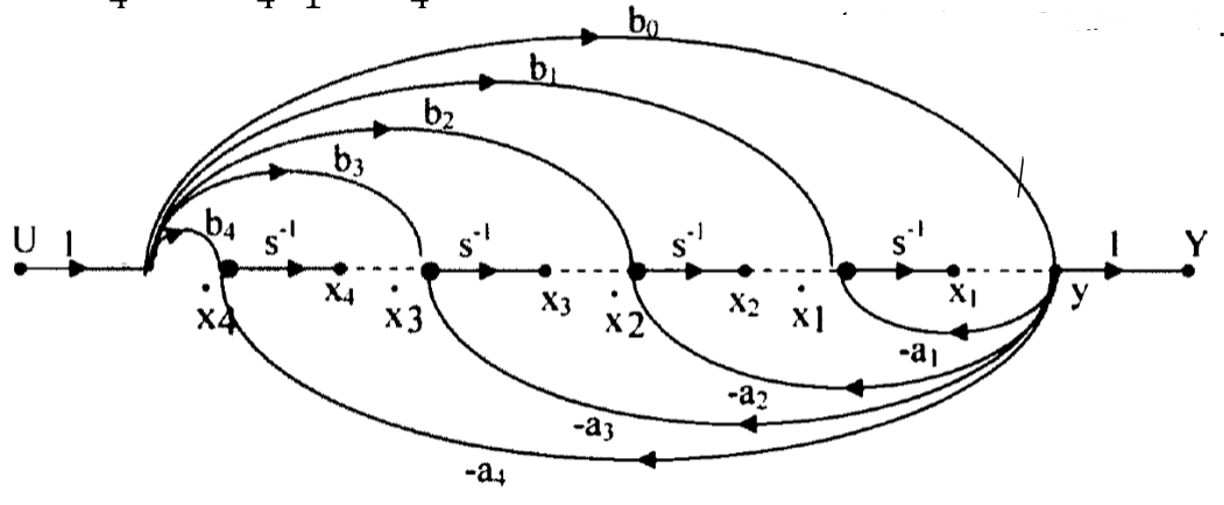
级联型
如果系统的传递函数\(\frac{Y(s)}{U(s)}\)写作:
\[\frac{Y(s)}{U(s)}=\frac{(s+z)}{∏^n(s+p_i)}\] 那么可以视为:
\[\frac{x_n}{u}=\frac{1}{s+p_n}⇒\dot{x_n}=-p_ix_n+u\] \[\frac{x_k}{x_{k+1}}=\frac{1}{s+k_n}⇒\dot{x_k}=-p_ix_k+x_{k+1}\] \[\frac{y}{x_1}=s+z⇒y=\dot{x_1}+zx_1\]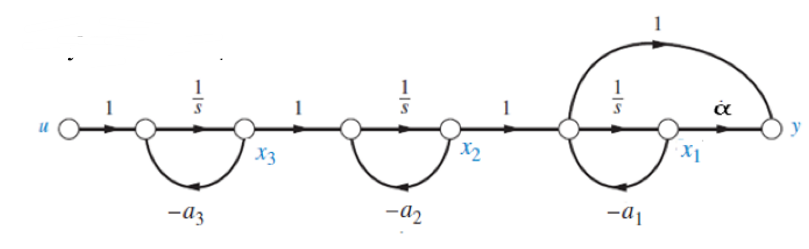
并联型
如果系统的传递函数\(\frac{Y(s)}{U(s)}\)写作:
\[\frac{Y(s)}{U(s)}=∑\frac{α_i}{(s+p_i)}\]
那么系统的状态方程可以写作:
\[\dot{x_i}=-p_ix_i+α_i\] 系统的输出方程可以写作:
\[y=∑α_ix_i\]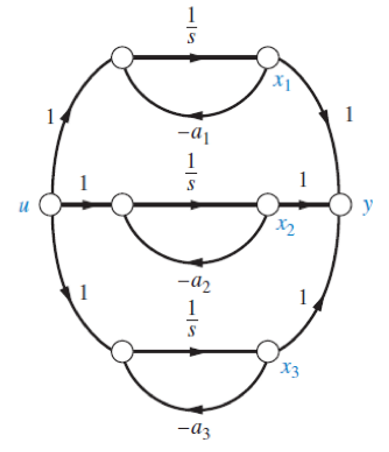
状态空间表示分析
状态空间转换传输函数
对于系统的状态方程:
\[\vec{\dot{x}}=A\vec{x}+Bu\] 由拉普拉斯变换得到:
\[s\vec{X}(s)=A\vec{X}(s)+B\vec{U}(s)\] 可以得到:
\[(sI-A)\vec{X}(s)=B\vec{U}(s)\] 整理可以得到:
\[\vec{X}(s)=[sI-A]^{-1}B\vec{U}(s)\] 令: \[Φ(s)=[sI-A]^{-1}\] 称其对应的矩阵\(ϕ(t)\)为状态转移矩阵(state transform matrix),其后会进一步讨论这个矩阵的作用。
将其带入系统的输出方程的拉普拉斯变换中:\(\vec{Y}(s)=C\vec{X}(s)+D\vec{U}(s)\),有:
\[\vec{Y}(s)=[CΦ(s)B+D]\vec{U}(s)\] 根据系统传递函数的定义可知:
\[T(s)=\frac{Y(s)}{U(s)}=C[sI-A]^{-1}B+D\] \([sI-A]\)的行列式\(|sI-A|\)结果为系统的特征多项式。
稳态误差
对于系统 \(\begin{cases} \vec{\dot{x}}=A\vec{x}+Bu\\
y=C\vec{x} \end{cases}\),根据稳态误差的定义:\(E(s)=\frac{1}{G(s)+1}R(s)\),有:
\[\begin{aligned}
E(s)&=R(s)[1-T(s)]\\
&=R(s)[1-C[sI-A]^{-1}B]
\end{aligned}\] 有终值定理:
\[e(∞)=\lim_{s→0}sE(s)=\lim_{s→0}R(s)[1-C[sI-A]^{-1}B]\]
- 当\(R(s)=1\)时,\(e(∞)=1+CA^{-1}B\)
- 当\(R(s)=s\)时,\(e(∞)=\lim_{t→∞}[(1+CA^{-1}B)t+C(A^{-1})^2B\)
系统分解(对角化)
对于系统 \(\begin{cases} \vec{\dot{x}}=A\vec{x}+Bu\\ y=C\vec{x}+Du \end{cases}\),现在指定一组新的状态变量\(z\),与\(x\)之间存在如下关系:
\[\vec{x}=P\vec{z}\] 且有\(\vec{\dot{x}}=P\vec{\dot{z}}\).
\(P\)称为转换矩阵是\(A\)的特征向量\(\vec{m}\)组成的矩阵\([\vec{m_1} \vec{m_2}...\vec{m_n}]\),带入系统的状态空间表示中,有:
\[\begin{cases} \vec{\dot{z}}=P^{-1}AP\vec{z}+P^{-1}Bu\\ y=CP\vec{z}+Du \end{cases}\] 可以发现\(P^{-1}AP\)是\(A\)的对角矩阵。
齐次状态方程和非齐次状态方程
已知系统的当前输入,则可以根据系统的状态方程求得系统的当前状态。简而言之,系统的当前状态就是系统状态方程的解。本小节将从简单的齐次状态方程入手寻找系统的当前状态。
齐次状态方程
对状态方程\(\vec{\dot{x}}=A\vec{x}+Bu\),B等于0时的情况称为齐次状态方程(Homogeneous state equation)。换言之,系统的齐次状态方程表示了系统在零输入下系统的前一个状态和当前状态之间的关系,是系统的零输入响应(Zero-state response)。
齐次状态方程的解
对于齐次状态方程\(\vec{\dot{x}}=A\vec{x}\),如果已知系统的初始状态\(x(0)\),那么可以求解到:
\[x(t)=e^{At}x(0)\] 这是齐次状态方程的解,称为零输入解,其物理意义是伺服系统的自由振动情况。
称\(ϕ(t)=e^{At}\)为该系统的状态转移矩阵(时域)。
状态转移矩阵
在数学上\(ϕ(t)=e^{At}\)与\(Φ(s)=[sI-A]^{-1}\)为拉普拉斯变换对:
\[ϕ(t)=e^{At}⇔Φ(s)=[sI-A]^{-1}\]
于是将\(ϕ(t)\)带入其次状态方程,其可以转化为:
\[x(t)=ϕ(t)x(0)\] \[x(t)=ϕ(t-t_0)x(t_0),t≥t_0\] 可以发现系统状态转移矩阵的作用是:已知系统在某一时刻\(t_0\)的系统状态\(x(t_0)\),通过系统的状态转移矩阵,可以得到系统在\(t_0\)任何一个时刻\(t\)的系统状态\(x(t)\)。
状态转移矩阵可以通过如下三种方法求得:
- 通过拉普拉斯反变换\([sI-A]^{-1}\)求得
- 根据泰勒展开式:
\[e^{At}=I+At+\frac{1}{2!}A^2t^2+\frac{1}{3!}A^3t^3+...+\frac{1}{k!}A^kt^k+...\] 进行近似计算。
- 如果状态矩阵\(A\)可以被写作约旦标准型\(A^{J}\),有:
\[e^{At}=Se^{A^Jt}S^{-1}\] 即\(e^{A^Jt}\)的对角矩阵。
- 如果状态矩阵\(A\)可以被对角化为\(A^D\),有:
\[e^{At}=Pe^{A^Dt}P^{-1}\] 即\(e^{A^Dt}\)的对角矩阵。
非齐次状态方程的解
非齐次状态方程\(\vec{\dot{x}}=A\vec{x}+Bu\)的解是系统输入不为0时的解,其物理意义是伺服系统的受迫振动情况。
非齐次状态方程的解的格式为:
- 如果已知初始状态\(x(0)\):
\[\vec{x}=e^{At}\vec{x}(0)+∫_0^te^{A(t-τ)}Bu(τ)dτ\] - 如果已知某一状态\(x(t_0)\): \[\vec{x}=e^{A(t-t_0)}\vec{x}(t_0)+∫_{t_0}^te^{A(t-τ)}Bu(τ)dτ\]
能控性和能观性
能控性
在某一时刻\(t_0\),如果系统可以通过控制向量将系统的状态\(\vec{x}(t_0)\)转变为系统的其他状态(即只要知道目前的状态,以后所有的状态都是已知的),则系统是能控的(controllable)。换言之,如果系统状态和系统输入是独立的,那么系统是能控的。
对于系统\(\begin{cases} \vec{\dot{x}}=A\vec{x}+Bu\\ y=C\vec{x}+Du \end{cases}\),它的状态方程是非齐次的,因此其状态方程的解为:
\[\vec{x}(t)=e^{A(t-t_0)}\vec{x}(t_0)+∫_{t_0}^te^{A(t-τ)}Bu(τ)dτ\] 假设\(\vec{x}(t_0)=0\),有:
\[\vec{x}(0)=-∫_{0}^{t_0}e^{-Aτ}Bu(τ)dτ\] 带入\(e^{-Aτ}=∑a_k(τ)A^k\),并令\(β_k=∫_0^{t_0}a_k(τ)u(τ)dτ\),可以得到:
\[\vec{x}(0)=-∑_{k=0}^{n-1}A^kBβ_k\] 矩阵化该表达式,有:
\[\vec{x}(0)=-[B|AB|A^2B|…|A^{n-1}B]\begin{bmatrix}
β_0\\
-\\
β_1\\
-\\
⋮\\
-\\
β_{n-1}
\end{bmatrix}\] 如果满足上述式子成立,则称系统是完全状态能控的(completely state controllable)。 其中由\(A\)及其幂和\(B\)的乘积向量扩增的矩阵\([B|AB|A^2B|…|A^{n-1}B]\)称为能控矩阵(controllability matrix),对于有\(n\)个状态的系统,它是一个\(n×n\)的方阵。通过之前的分析可以发现,当且仅当能控矩阵满秩,即其秩为\(n\)时,系统是完全状态能控(state controllable)的。
满秩的等价条件:
- 组成扩增矩阵的向量\(A^{i-1}B\)线性无关
- 控制矩阵的行列式结果不为0
同样地,如果将齐次方程的解带入到系统的输出方程,同理也可以在计算过程中得到一个\(m × (n+1)\)的输出内控矩阵:
\[[CB|CAB|CA^2B|…|CA^{n-1}B|D]\] 当且仅当输出能控矩阵满秩即其秩为\(m\)(或者说组成扩增矩阵的向量\(CA^{i-1}B\)线性无关/输出控制矩阵行列式结果不为零)时,系统是完全输出能控(output controllable)的。
能观性
在某一时刻\(t_0\),如果系统可以通过在有限时间内的输出(由输出矩阵和控制矩阵两部分决定)来判断系统初始状态\(\vec{x}(0)\),则系统是能观的(observable)。系统的能观性与系统输出有关。
对其次系统\(\begin{cases} \vec{\dot{x}}=A\vec{x}\\ y=C\vec{x} \end{cases}\)而言,其能观矩阵(observability matrix)是一个\(n×nm\)的矩阵:
\[[C^T|A^TC^T|(A^T)^2C^T…|(A^T)^{n-1}C]\] 当系统的能观矩阵满秩(或者说组成扩增矩阵的向量\((A^T)^{i-1}C\)线性无关/能观矩阵行列式结果不为零)时,表明系统是完全能观的(completely observable)。
对偶
系统的能控性和能观性是对偶的。
有如下结论:
对于系统I:\(\begin{cases} \vec{\dot{x}}=A\vec{x}+Bu\\ y=C\vec{x} \end{cases}\)和系统II:\(\begin{cases} \vec{\dot{z}}=A^T\vec{z}+C^T\vec{v}\\ \vec{n}=B^T\vec{z} \end{cases}\),有:
如果系统I完全状态能控,那么系统II完全能观。
快速判断法
对于写作标准形式的系统矩阵,有可以根据状态矩阵\(A\)、\(B\)和\(C\)的形状快速判断系统能观性和能控性的方法。
对于约旦标准型:
- 如果对应\(A^J\)最后一列的矩阵\(B\)或者\(S^{-1}B\)(\(S\)是将\(A\)转换为其约旦标准型\(A^J\)的转换矩阵)中的任意一行非零,同时\(B\)或者\(S^{-1}B\)中对应特征值的行非零,那么系统是能控的。
- 如果对应\(A^J\)第一列的矩阵\(CS\)或\(C\)非零,同时\(C\)或者\(CS\)中对应特征值的非列零,那么系统是能观的。
对于对角型:
- 如果\(B\)不含有非零行,则系统是能控的。
- 如果\(C\)不含任何非零列,则系统是能观的。
可镇定性和可探测性
特征向量的模
另外,某些系统可能呈现一定的能控性和能观性,称为部分能控或部分能观系统。此时可以通过探究状态矩阵\(A\)的特征值\(λ_i\)来研究每一个特征向量对应的模对系统可镇定性、能控性、能观性的贡献。
- 如果状态矩阵\(A\)的特征值\(λ_i\)在坐标轴左半平面,称其对应的模是可镇定的。
- 如果矩阵\([(λ_iI-A)B]\)满秩,那么特征值\(λ_i\)对应的模是能控的。
- 如果矩阵\(\begin{bmatrix} (λ_iI-A)\\ C \end{bmatrix}\)满秩,那么特征值\(λ_i\)对应的模是能观的。
可镇定性和可探测性的定义和对偶
对于一个部分可控的系统,如果非可控的模都稳定,且不稳定的模都可控,那么系统是可镇定(stablizable)的。
对于一个部分能观的系统,如果非能观的模都稳定,且能观的模都不稳定,那么系统是可探测(detectable)的。
对于完全能控的系统,它是可镇定的。
对于完全能观的系统,它是可探测的。
可以发现,可探测性和可镇定性是对偶的。