10. 连续系统状态空间的补偿器设计

连续系统状态空间的补偿器设计

通过频率响应进行设计的缺陷是：
当系统的阶数高于2后，由于缺少用来高阶近似的参数而无法改进系统特定的极点。
状态空间中的设计可以通过一些数学方法寻找到这些参数，并对闭环系统特定的极点进行调整。
状态空间中的设计分为两部分:
- 控制器（controller）设计：通过指定控制器增益将状态变量反馈给系统的输入\(u\)。
- 观测器（observer）设计：通过指定观测器增益将实际输出与估计输出之间的误差反馈给状态变量的微分。

上述两种设计中的增益可以通过匹配设计要求的系统特征方程与实际的系统特征方程的系数来得到。

全状态反馈控制器设计

对于一个n阶反馈控制系统，其闭环特征方程为：
\[s^n+a_{n-1}s^{n-1}+a_1s+a_0=0\] 这\(n\)个方程系数\(a_i\)会决定系统极点所在的位置。因此全状态反馈控制器(full-state feedback controller)的设计思路是引入\(n\)个可调整的参数\(k_i\)对系统特征方程的系数\(a_i\)进行调整，进而使得系统极点能够在设计要求的位置。这样的思路前提是系统是能控的。

在全状态反馈控制器中，由\(n\)个可调整的参数\(k_i\)组成的向量\(K\)被添加在了反馈回路中，如下图所示：

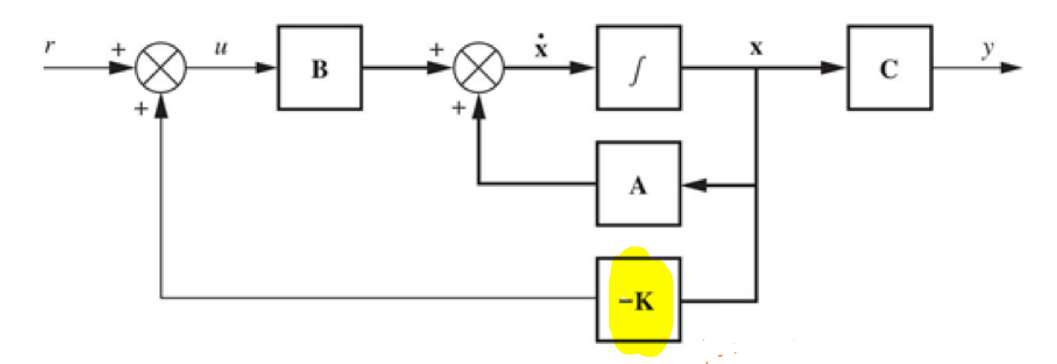
根据系统框图可以得到系统的状态空间表示：
\[\vec{\dot{x}}=A\vec{x}+Bu=(A-BK)\vec{x}+Br\] \[y=C\vec{x}\]

如此，新的状态转换矩阵为：\(Φ(s)=[sI-(A-BK)]\).
根据状态转换矩阵，可以得到改进后的系统特征方程为：
\[|Φ(s)|=|sI-(A-BK)|=0\]

设计目标

系统设计的准则是：
- 阶跃响应更快的达到稳定 - 增加系统的稳定性 根据系统的稳定性准则，系统的设计更需要极点在s域左半平面并且远离s平面的虚轴。可以通过增大控制器的增益\(K\)来得到符合要求的极点。

此外，可以通过增加额外的极点来与系统现有的零点抵消，更能增加系统的稳定性。

设计步骤

相位变化型设计

如果系统以相位变化型给出：
- 检查系统原型的稳定性 - 根据系统设计要求中的过冲率和设置时间计算出系统要求的阻尼比\(ζ\)和固有频率\(ω_n\)，构建系统的二阶极点项：\((s^2+2ζω_ns+ω_n^2)\)
- 如果系统原型存在零点\((s+z)\)，则添加新的极点项\((s+p),p=z\)。
（此时可以得到设计要求的极点多项式为：\((s+p)(s^2+2ζω_ns+ω_n^2)\)） - \(n\)个反馈控制系数\(-k\)，并计算得到矩阵\(A-BK\)。
- 找到改进后系统的特征方程\(|sI-(A-BK)|=0\)。
- 将\(|sI-(A-BK)|=0\)与\((s+p)(s^2+2ζω_ns+ω_n)=0\)的系数进行匹配，使用待定系数法即可得到所有的\(k\)

非相位变化型设计

如果系统原型没有以相位变化型给出\(\begin{cases} \vec{\dot{z}}=A_z\vec{z}+B_zu\\ y=C_z\vec{z} \end{cases}\)，那么可以假设有映射关系\(\vec{z}=P\vec{x}\)使得系统的状态空间表示为相位变化型。
那么有：
\[\vec{\dot{x}}=P^{-1}A_xP\vec{x}+P^{-1}B_xu\] \[y=C_xP\vec{z}\] 变换前后的控制矩阵和反馈控制向量有如下关系：
\[C_z=PC_x\] \[K_z=K_xP^{-1}\] 那么可以得到：
\[P=C_zC^{-1}_x\] 其中：\(C_z\)是系统非相位变化型表示中的控制矩阵，\(C_x\)是系统相位变化型表示中的能控矩阵。

所以基本思路是：
- 求得现在系统的控制矩阵\(C_z=[B_z|A_zB_z|…|A_z^{n-1}B_z]\) - 根据\(|sI-A_z|=0\)找到现在系统的特征方程。
- 根据特征方程，写出系统状态空间表示的相位变化型，找到系统相位变化型的能控矩阵\(C_x=[B_x|A_xB_x|…|A^{n-1}_xB_x]\) - 检验能控性。
- 根据\(P=C_zC^{-1}_x\)得到\(P\) - 根据相位变化型中的\(A_x\)，\(B_x\)，找到\(A_x-B_xK_x\)，并得到目标系统的特征方程\(|sI-(A_x-B_xK_x)|=0\) - 根据设计目标求出\(ω_n\)和\(ζ\)，并构造系统的特征方程。
- 将系统的特征方程与\(|sI-(A_x-B_xK_x)|=0\)进行系数匹配，得到\(K_x\) - 利用\(K_z=K_xP^{-1}\)得到\(K_z\)

全状态观测器

在实际工程中，测量系统的全部状态的开销非常大。观测器(observer/state estimator)可以预测系统状态并反馈，以此来减少需要测量的系统状态，进而节省设计支出。

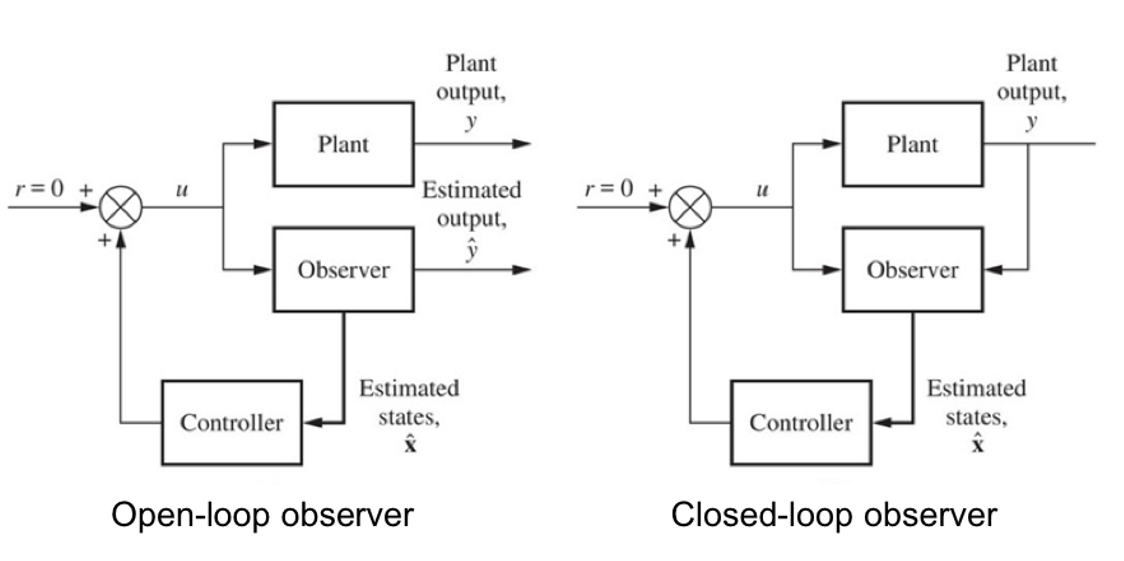
同全状态控制器的设计思路，全状态观测器通过设计一个常数向量\(L\)，使观测器的瞬态响应比受控回路的响应快，从而得到系统状态向量的快速更新估计。观测器的设计要求系统原型必须是能观的。
观测器系统的框图如下图所示：

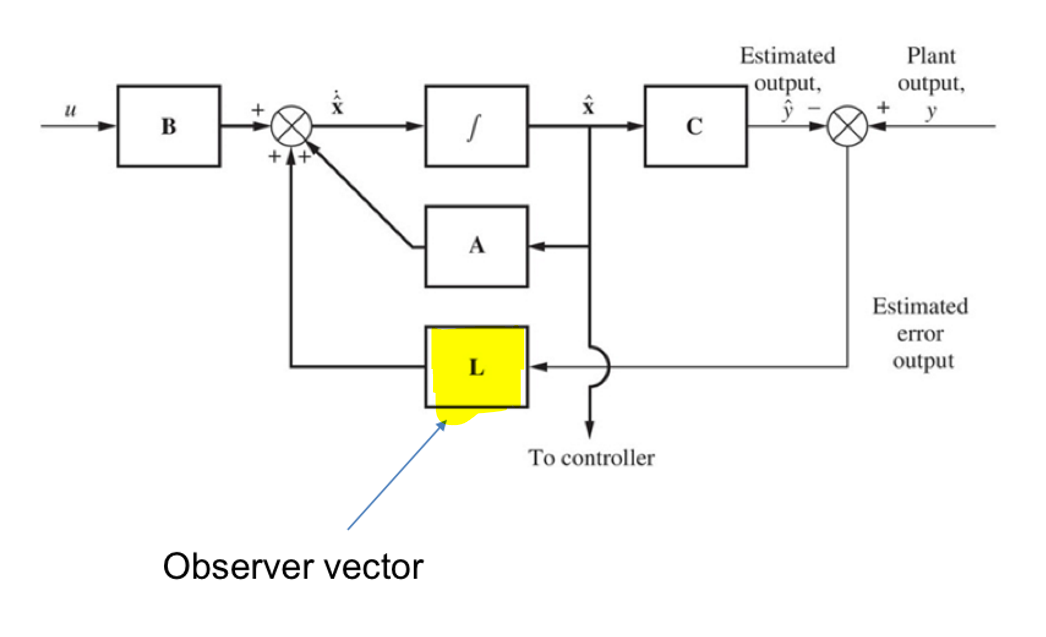
整个系统又称为误差系统(error system)。

设误差系统的状态误差为\(\vec{\hat{x_e}}=\vec{x}-\vec{\hat{x}}\)表示实际状态与观测器估计的差异：

与系统原型的状态空间表示\(\begin{cases} \vec{\dot{x}}=A\vec{x}+Bu\\ y=C\vec{x} \end{cases}\)相减，得到：
\[\vec{\dot{x}}-\vec{\dot{\hat{x}}}=A(\vec{x}-\vec{\hat{x}})-L(y-\hat{y})\] \[y-\hat{y}=C(\vec{\dot{x}}-\vec{\dot{\hat{x}}})\] 进一步得到：
\[\vec{\dot{x}}-\vec{\dot{\hat{x}}}=(A-LC)(\vec{x}-\vec{\hat{x}})\] \[y-\hat{y}=C(\vec{\dot{x}}-\vec{\dot{\hat{x}}})\]

误差系统的特征方程为：
\[|sI-(A-LC)|=0\]

设计步骤

• 将系统原型改写为能观标准型，并检查系统原型的能观性。
  
• 根据系统原型的能观标准型，得到其状态转移矩阵\(Φ=A-LC\)
• 根据系统的状态转换矩阵得到含有观测系数\(l\)的系统特征方程：\(|sI-(A-LC)|=0\)
  
• 根据对系统设计的要求计算出要求的阻尼比\(ζ\)和固有频率\(ω_n\)，构造目标系统的特征方程。
  
• 将目标系统的特征方程与\(|sI-(A-LC)|=0\)匹配，使用待定系数法得到观测向量\(L\)中的每一个元素\(l\)。

当原型系统\(\begin{cases} \vec{\dot{z}}=A\vec{z}+Bu\\ y=C\vec{z} \end{cases}\)没有以能观标准型给出时，那么可以假设有映射关系\(\vec{z}=P\vec{x}\)使得系统的状态空间表示为能观标准型。
那么有：
\[\vec{\dot{x}}=P^{-1}AP\vec{x}+P^{-1}Bu\] \[y=CP\vec{x}\] 变换前后的控制矩阵和反馈控制向量有如下关系：
\[O_z=PO_x\] \[L_z=L_xP^{-1}\] 那么可以得到\(P=O_zO^{-1}_x\)和\(L_z\)。
所以基本思路是：
- 找到现在系统的能观矩阵\(O_z\)
- 根据\(|sI-A|=0\)找到现在系统的特征方程。
- 根据特征方程，写出系统状态空间表示的能观标准型，找到系统的能观矩阵\(O_x\)并检验能观性。
- 根据\(P=O_z^{-1}O_x\)得到\(P\) - 根据相位变化型中的\(A_x\)，\(B_x\)，找到\(A_x-L_xB_x\)，并得到目标系统的特征方程\(|sI-(A_x-L_xB_x)|=0\) - 根据设计目标求出\(ω_n\)和\(ζ\)，并构造系统的特征方程。
- 将系统的特征方程与\(|sI-(A_x-L_xB_x)|=0\)进行系数匹配，得到\(L_x\) - 利用\(L_z=L_xP^{-1}\)得到\(L_z\)

控制器和观测器的对偶性

可以发现，控制器的设计方法和观测器的设计方法几乎一样。事实上，控制器系统和观测器系统在数学上呈现对偶性。
如果控制器系统的状态空间表示系数矩阵为\(A\),\(B\),\(C\)，
那么观测器系统的状态空间表示系数矩阵为\(A^T\),\(C^T\),\(B^T\)。
在MATLAB中，观测器系统和控制器系统的控制系数和观测系数向量都用命令place()生成，对控制器系统：K=place(A,B,p)
对观测器系统：L=place(A',C',p).
其中p是闭环系统所有极点组成的向量。

观测器和控制器的连接

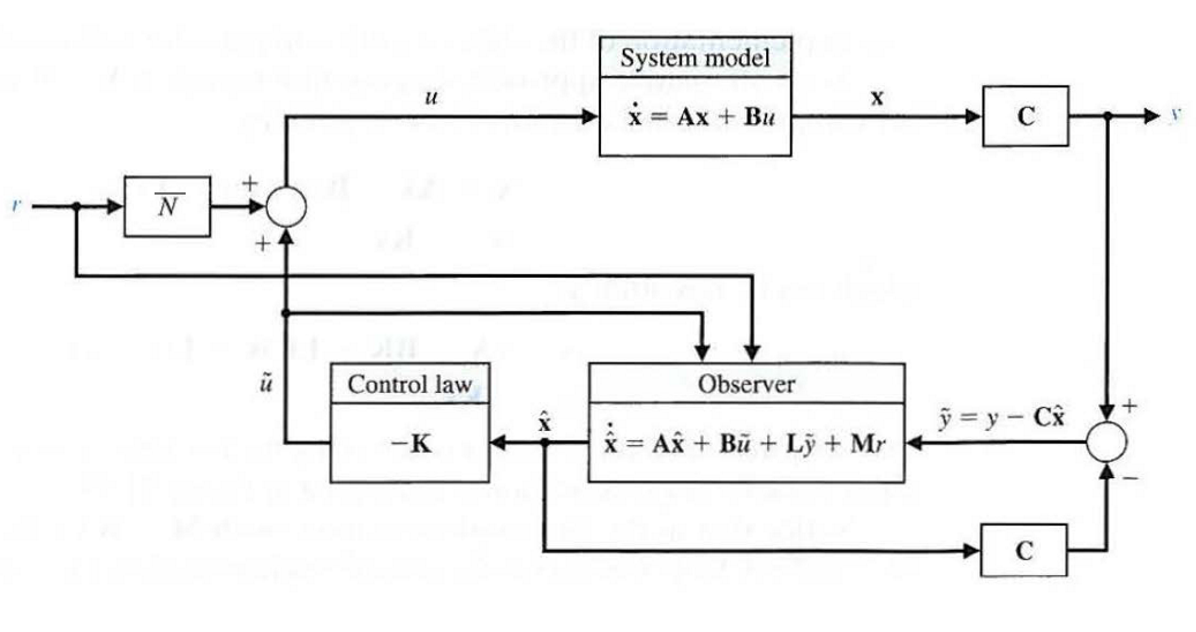
整个系统连接观测器和控制器后如图所示：

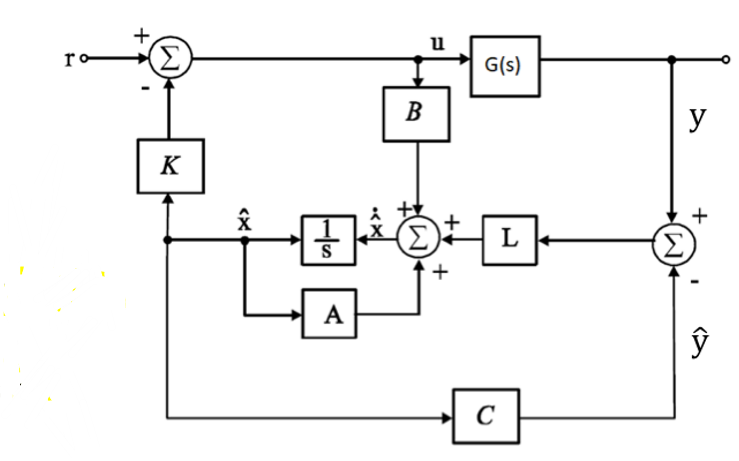
引入系统输入

在完成对观测器和控制器的设计之后，整个系统的状态空间表示为：
\[\vec{\dot{\hat{x}}}=A\vec{\hat{x}}+Bu+L(y-\hat{y})\] \[y=C\vec{\hat{x}}\] 同时，根据系统框图有：
\[u=-K\vec{\hat{x}}+r\] 带入状态方程，得到：
\[\vec{\dot{\hat{x}}}=A\vec{\hat{x}}+B(-K\vec{\hat{x}}+r)+L(y-C\vec{\hat{x}})\] 整理后有：
\[\vec{\dot{\hat{x}}}=(A-BK-LC)\vec{\hat{x}}+Ly+Br\] 通常增加常量\(N\)和向量\(\vec{M}\)以便进行调整：
\[\vec{\dot{\hat{x}}}=(A-BK-LC)\vec{\hat{x}}+Ly+\vec{M}r\] \[u=-K\vec{\hat{x}}+Nr\]

全状态反馈

在全状态反馈中，使用向量\(\vec{N_x}\)和标量\(N_u\)对系统进行调整：

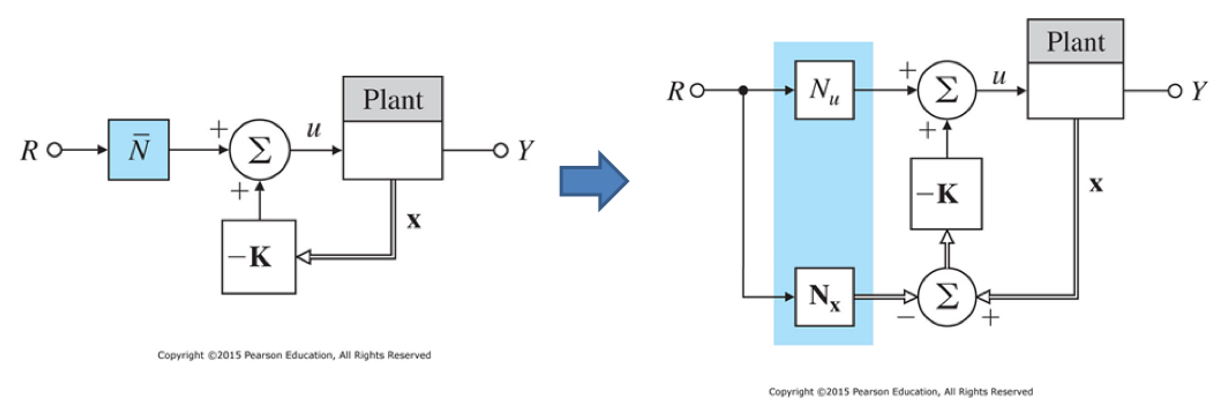
有：
\[\overline{N}=n_u+K\vec{n_x}\] 为了使稳态条件下\(y=r\)，令\(\vec{x}=\vec{n_x}r\),\(u=n_ur\)，在稳态条件下，系统状态的微分为0，有：
\[0=A\vec{n_x}r+Bn_ur\] \[1=C\vec{n_x}+Dn_u\] 进一步矩阵化方程，有：
\[\begin{bmatrix} 0 \\ 1 \end{bmatrix}=\begin{bmatrix} A & B \\ C & D \\ \end{bmatrix}\begin{bmatrix} \vec{n_x}\\ n_u \end{bmatrix}\] 即：
\[\begin{bmatrix} \vec{n_x}\\ n_u \end{bmatrix}=\begin{bmatrix} A & B \\ C & D \\ \end{bmatrix}^{-1}\begin{bmatrix} 0 \\ 1 \end{bmatrix}\] 通过上述式子可以求得向量\(\vec{n_x}\)和标量\(n_u\)。
此时系统的传输函数为：
\[\frac{Y(s)}{R(s)}=\overline{N}C(sI-A+BK)^{-1}B\]

Zero-assignment Estimator

根据如下的公式,对I型控制系统：
\[\frac{1}{K_v}=∑\frac{1}{z_i}-∑\frac{1}{p_i}\] \(z_i\)和\(p_i\)分别是整个系统的闭环零点和极点。
上述公式被称为Truxal误差常数计算公式，可以发现通过改变系统的零点和极点分布，可以改变系统的速度误差常数\(K_v\)。可以发现，当闭环极点远离虚轴时，速度误差常数\(K_v\)会增大。
对系统\(\begin{cases} \vec{\dot{\hat{x}}}=(A-BK-LC)\vec{\hat{x}}+Ly+\vec{M}r\\ u=-K\vec{\hat{x}}+\overline{N}r \end{cases}\)，经过计算可以发现系统的零点由如下方程确定：
\[|sI-A+BK+LC-\frac{M}{N}K|=0\] > 计算过程详见：
> https://zhuanlan.zhihu.com/p/111317278#:~:text=Compensator%EF%BC%9A%E8%A7%82%E6%B5%8B%E5%99%A8%E4%B8%8E%E6%8E%A7%E5%88%B6%E5%BE%8B%E7%9A%84%E7%BB%93%E5%90%88%20Observer-Based%20Controller

可以发现，通过设置\(N\)和\(M\)就可以自由配置零点。这样的配置称为Zero-assignment Estimator。

补偿器设计

简单来说，补偿器就是系统的控制器和观测器的结合：在反馈回路上，系统的误差可以被观测器捕捉，并将误差传递给控制器，由控制器对系统进行调整，并输出补偿值并在前项传输过程中对系统输入进行调整，使得可以进一步减小系统误差。这样的系统行为称为补偿(compansation)。

反馈补偿

对于系统\(\begin{cases} \vec{\dot{\hat{x}}}=(A-BK-LC)\vec{\hat{x}}+Ly+\vec{M}r\\ u=-K\vec{\hat{x}}+\overline{N}r \end{cases}\)，如果选择\(M=B\overline{N}\)，并且带入\(u=-K\vec{\hat{x}}+\overline{N}r\)即可得到：
\[\vec{\dot{\hat{x}}}=(A-LC)\vec{\hat{x}}+Ly+Bu\] \[u=-K\vec{\hat{x}}+\overline{N}r\] 如此，观测器的输入将观测系统输出的反馈\(y\)和控制器的输出\(u\)，这样的补偿形式称为系统的反馈补偿/标准形式（standard case)：

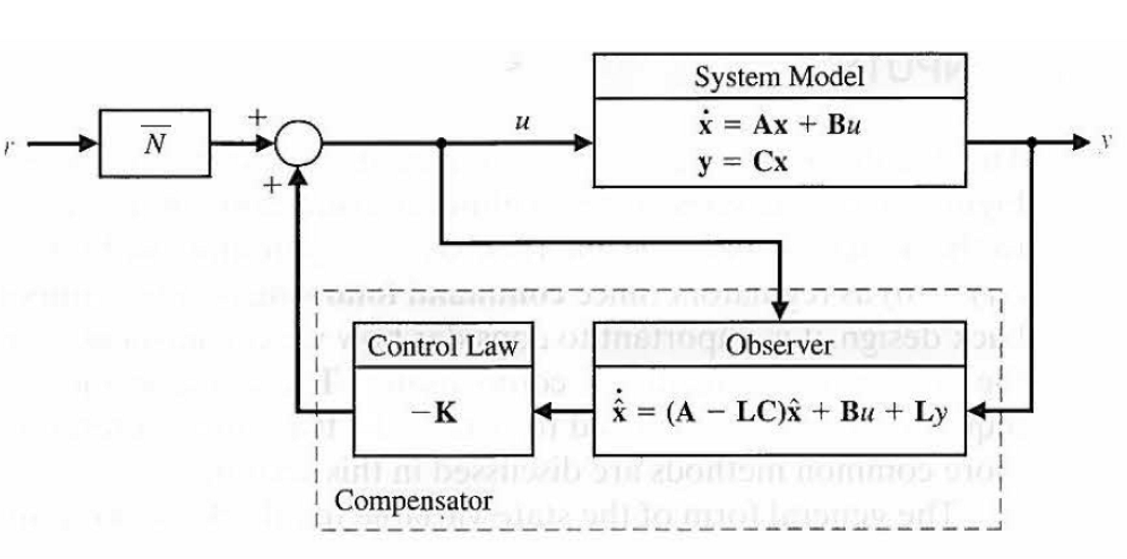
此时系统的特征方程为：
\[|sI-A+BK|=0\] 可以发现系统的特征方程与控制器的特征方程一致。在这种设置下，通过设置控制器的话参数就可以调整整个系统的极点分布，因此这种形式的补偿器通常是设置补偿系统的最优方案。

串联补偿

补偿器的串联补偿/标准形式（classical case）如下图所示：

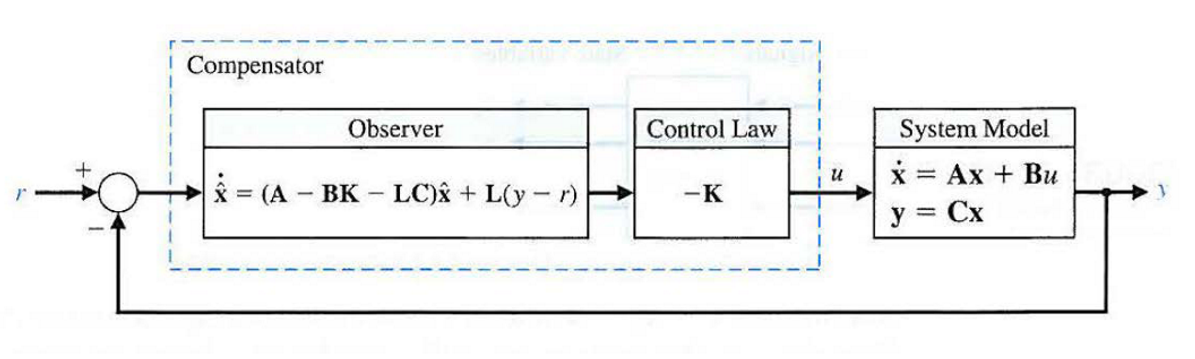
对于系统\(\begin{cases} \vec{\dot{\hat{x}}}=(A-BK-LC)\vec{\hat{x}}+Ly+\vec{M}r\\ u=-K\vec{\hat{x}}+\overline{N}r \end{cases}\)，如果选\(\overline{N}=0,M=-L\)，那么有：
\[\vec{\dot{\hat{x}}}=(A-LC-BK)\vec{\hat{x}}+L(y-r)\] \[u=-K\vec{\hat{x}}+\overline{N}r\] 可以发现通过这样的参数设置可以将状态方程中的观测器输入改为\(y-r\)，即系统误差\(e\).
此时，系统的特征方程为：
\[|sI-A+BK||sI-A+LC|=0\] 整个系统的极点由观测器和控制器共同决定。
此时系统补偿器的传递函数为：
\[D_c(s)=-\frac{U(s)}{Y(s)}=K(sI-A+BK)\]

积分控制

补偿系统的问题在于，控制器和观测器的引入都会导致非常大的稳态误差。其次，虽然可以通过选择合适的\(\overline{N}\)来让稳态误差归零，但是这样的方法鲁棒性低，系统原型中任何参数的改变都会让稳态误差重新不为0.
解决问题的思路是利用积分项能够增加系统的类的同时将系统误差减小到0的特点，在系统控制器之前增加一个增益为\(K_e\)的积分单元，这种方法称为积分控制。

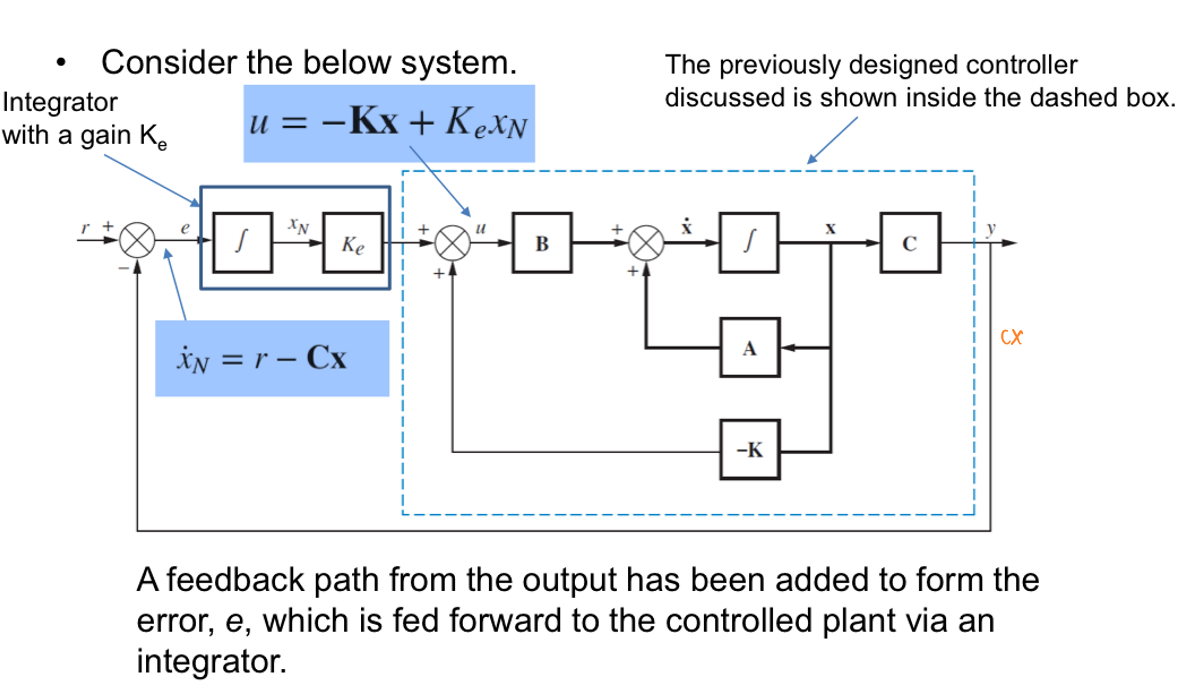
此时系统的状态空间表示为：
\[\vec{\dot{x}}=A\vec{x}+Bu\] \[\dot{x_N}=-C\vec{x}+r\] \[y=C\vec{x}\] 有：
\[\begin{bmatrix} \vec{\dot{x}}\\ \dot{x_N} \end{bmatrix}=\begin{bmatrix} A & 0\\ -C & 0 \end{bmatrix}\begin{bmatrix} \vec\\ x_N \end{bmatrix}+\begin{bmatrix} B\\ 0 \end{bmatrix}u+\begin{bmatrix} 0\\ 1 \end{bmatrix}r\] 同时，\(u=-K\vec{x}+K_ex_N=-[K -K_e]\begin{bmatrix} \vec{x} \\ x_N \end{bmatrix}\)， \[\begin{bmatrix} \vec{\dot{x}}\\ \dot{x_N} \end{bmatrix}=\begin{bmatrix} A-BK & BK_e\\ -C & 0 \end{bmatrix}\begin{bmatrix} \vec\\ x_N \end{bmatrix}+\begin{bmatrix} 0\\ 1 \end{bmatrix}r\] \[y=\begin{bmatrix} C & 0 \end{bmatrix}\begin{bmatrix} \vec\\ x_N \end{bmatrix}\] 同样地，根据这个方程可以得到特征多项式为：
\[|sI-\begin{bmatrix} A-BK & BK_e\\ -C & 0 \end{bmatrix}|\]

设计流程

• 利用设计要求设计控制器，并找到控制矩阵\(K\)
• 利用设计要求构造新的特征多项式
• 利用行列式\(|sI-\begin{bmatrix} A-BK & BK_e\\ -C & 0 \end{bmatrix}|\)得到含有\(K_e\)的特征多项式
• 系数匹配，得到\(K_e\)