11. 数字控制系统概述

数字控制系统概述

数字控制系统的特点

数字控制系统的核心是控制器的数字化，起到系统控制作用的控制器通常是微处理器、微控制器或者是电脑。数字控制系统中，数字控制器的输入和输出信号都是数字信号。
相比于模拟控制系统，采用数字信号对系统进行控制的优点是：
- 对噪声的鲁棒性好
通过与设立的判决门限阈值比较可以直接还原数字信号。
电子系统中的电容和电阻等器件的实际值往往会有公差，这些公差对数字信号不会起到很大的影响。
- 灵活性高
模拟控制器被硬件实现后很难再改动和重设计。但是数字控制器可以通过软件实现，并且往往不用将整个控制器全部重做就可以进行改动。
- 处理速度快
得益于计算机处理速度的发展，相比于模拟控制器，数字控制器的处理速度更快。采样间隔可以达到非常小的程度。
- 成本
由于大规模集成电路的发展，数字控制器的价格更低，占用空间也更小。

数字控制系统的基本结构

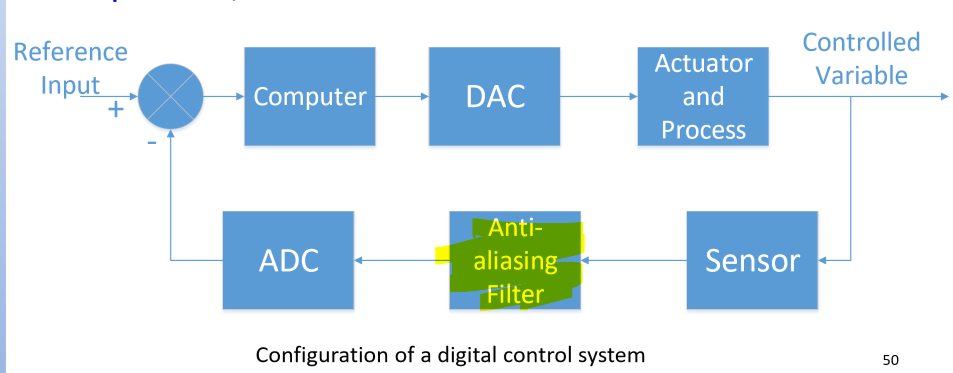
在结构上，由于数字控制器只能输入和输出数字信号，因此在数字控制器的输入输出两端应该设置模数转换器（ADC）和数模转换器（DAC）。

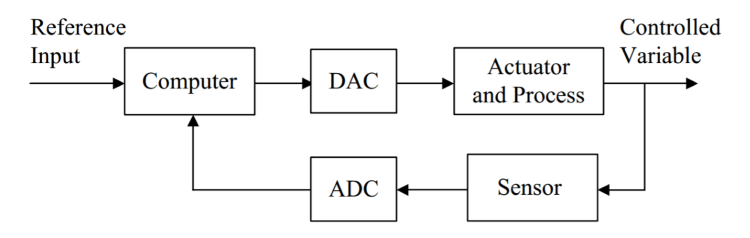
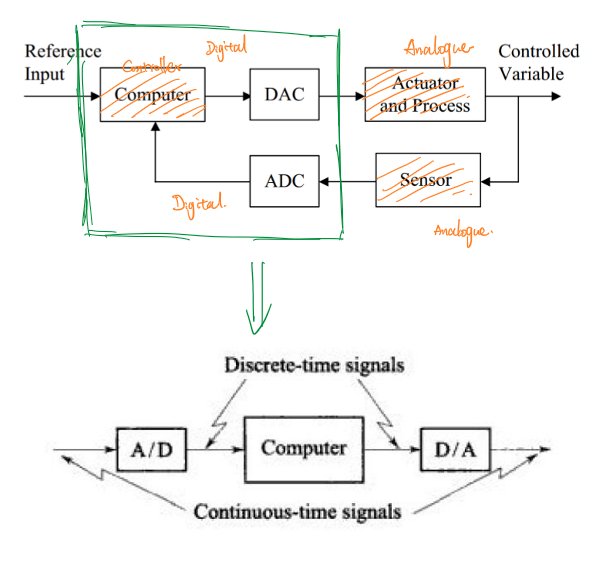
模数转换器

模数转换器是一种将模拟信号转变为数字信号的转置，它为数字控制器提供了数字信号和模拟信号的接口。
模拟信号转化为数字信号的过程可以概括为：“采样-量化-编码”。在采样阶段，幅值和时间连续的模拟信号经过采样，转变为离散时间，幅值连续的采样信号，采样信号通过量化后规整幅值，得到幅值和时间都离散的数字信号。数字信号通过编码器编码可以被解读为各种信息。

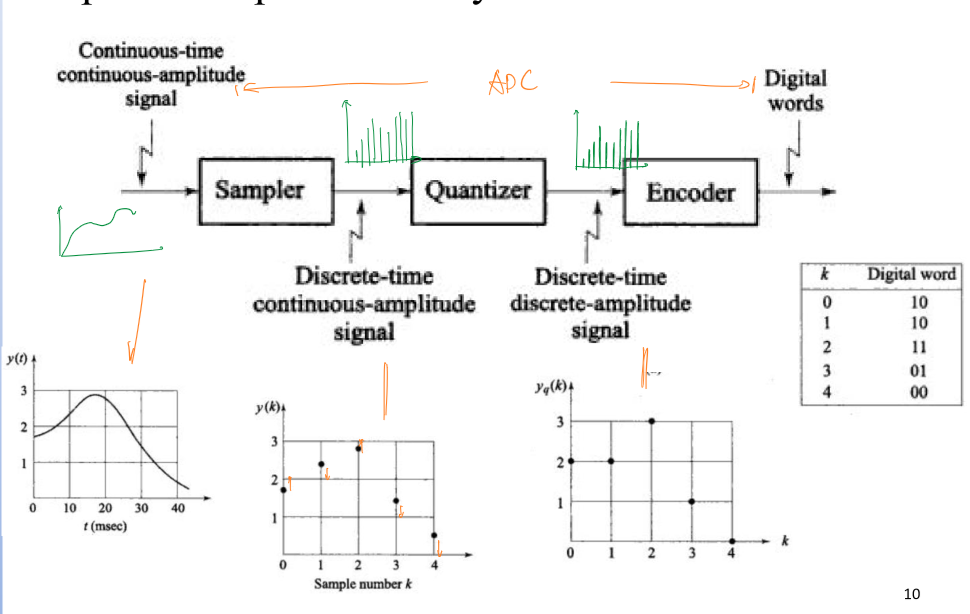
采样

采样过程需要遵守奈奎斯特采样准则，即采样频率需要大于或等于基带信号最高频率的两倍，这样才能保证模拟信号被准确的采样：
\[f_s≥2f_H\] 采样的方式有两种：
- 周期采样
对模拟信号进行等时间间距的采样。
- 多采样率采样
对于不同的反馈信号环路采样精度的不同，使用不同的采样率进行采样。

• 混叠
  当采样频率设置不合理时，即采样频率低于2倍的信号频率时，会导致原本的高频信号被采样成低频信号，这样的问题称为混叠(Aliasing)。
  
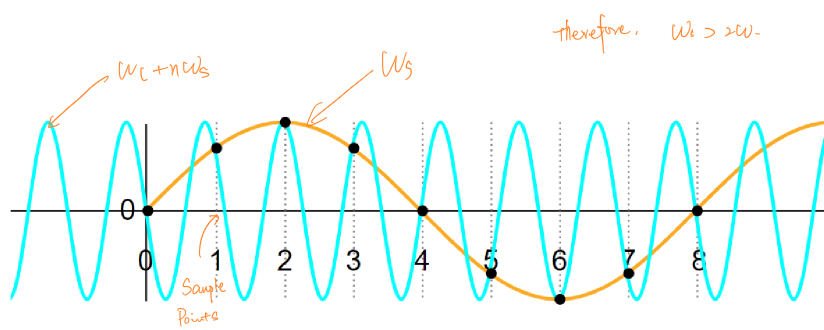
  混叠的解决方法有两种：
  • 设置采样频率大于\(2f_H\)
  • 使用低通滤波器称为抗混叠滤波器(anti-aliasing filter)添加在模数转换器之前。
  

量化

量化是用一段特定数值对采样结果进行近似的过程。
对于均匀量化，对于如果使用\(n\)个0/1比特对结果进行量化，那么量化级的大小为：
\[\frac{FSR}{2^n}\] \(FSR\)表示采样值范围的最大值。

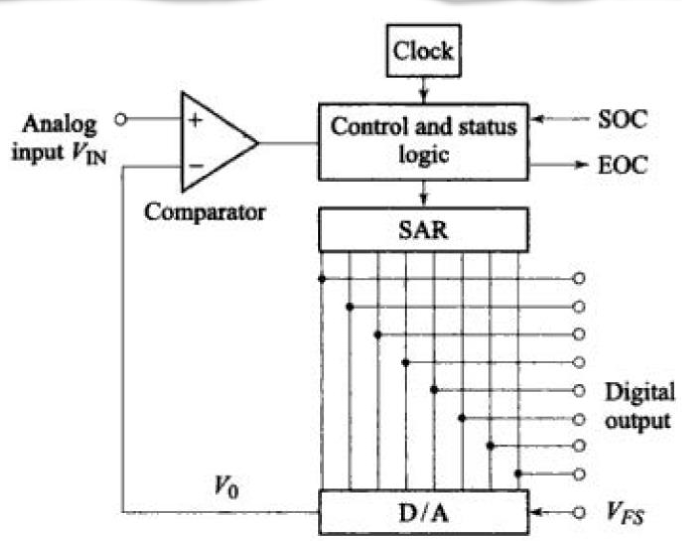
逐次逼近式ADC

下图中8bit Register的值的从MSB开始进行比特反转0->1，每一个比特位0->1的变化都会由DAC转换为电压与输入电压进行对比，比较器将两个电压进行对比，判断DAC的电压是否高于输入电压：如果输入电压高于DAC的电压，那么Register中这一比特位的值为1，如果低于DAC的电压，那么Register中这一位比特位的值恢复为0。
调整8bit Register的每一个比特位，直到LSB调整完毕，ADC的转换结束。

数模转换器

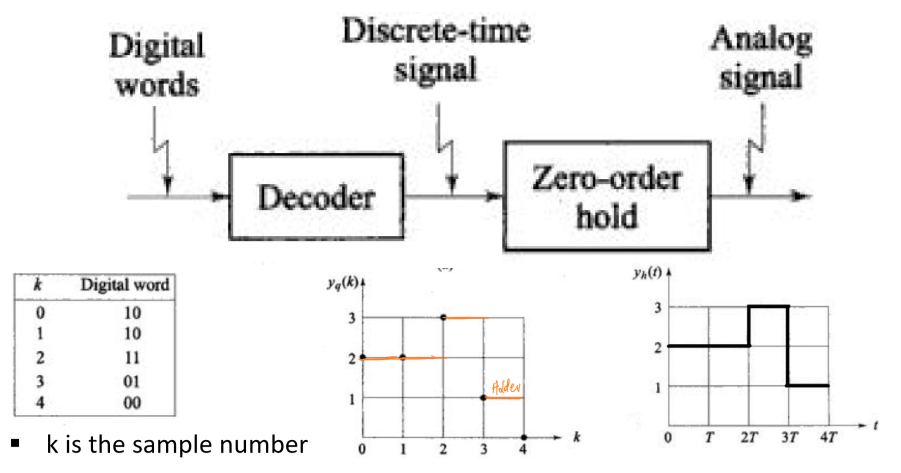
数模转换器是一种将数字信号转换为模拟信号的转置。数模转换的过程可以分为“解码-零阶保持（zero-order hold）”两个步骤。
数字信息通过解码转换为数字信号，离散的数字信号通过零阶保持器将每个时间点的电平值保持一段时间，进而形成时间和幅值连续的数字信号。

数模转换器电路

数模转换器电路有两种实现方法：
- T型电阻DAC(R-2R ladder network DAC)

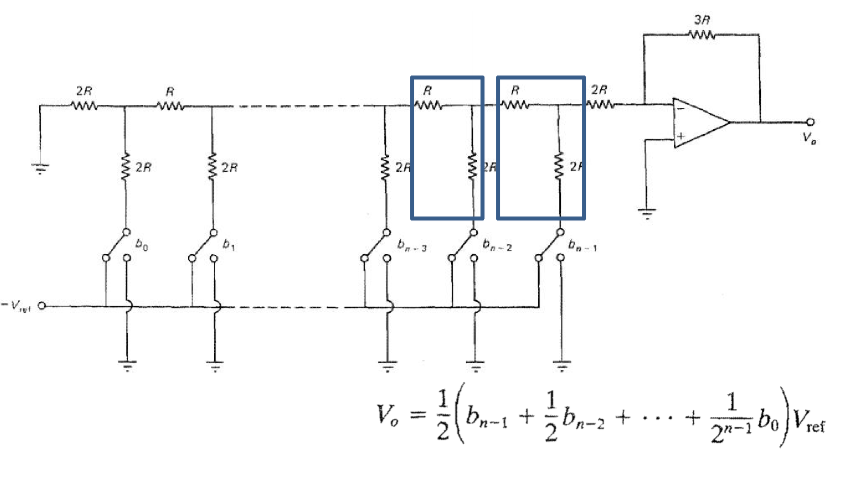
对于使用\(n\)个比特的量化，电路中存在\(n-1\)个“\(R-2R\)”的电阻电路。\(b_0\)为最低位，\(b_{n-1}\)为最高位。当\(b_i=0\)时，对应“\(R-2R\)”电路接地，当\(b_i=0\)时，对应“\(R-2R\)”电路与\(-V_{ref}\)连接。\(V_{ref}\)是采样电平的最大值，即\(FSR\)。
通过对电路的分析，有：
\[V_o=\frac{I_{bin}}{2^n}V_{ref}\] 其中\(I_{bin}=[b_{n-1}b_{n-2}...b_1b_0]\)

• 权电阻型DAC(weighted resistors DAC)
  权电阻型数模转换器要使用权电阻网络，其中电阻值为2的0次幂、1次幂、2次幂、3次幂等。
  

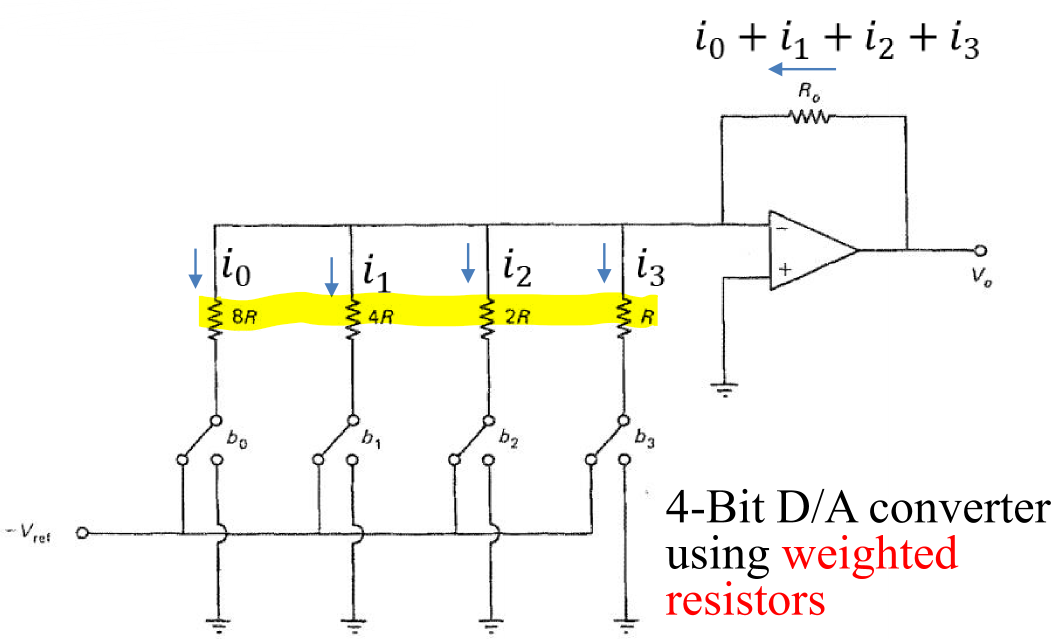
  权电阻型DAC在实现过程上很简单，但是由于使用了更多和更大的电阻值，难以获得足够精度的\(2^n\)电阻值，所以权电阻网络实际中比较难以使用。
  T型电阻DAC在实现过程中更为复杂，但是由于只需要\(R\)和\(2R\)两种电阻值，可以保证其精度。

零阶保持器

零阶保持器可以将给定信号保持一段时间，零阶保持器的时域表达式为：
\[u(t)-u(t-T)\]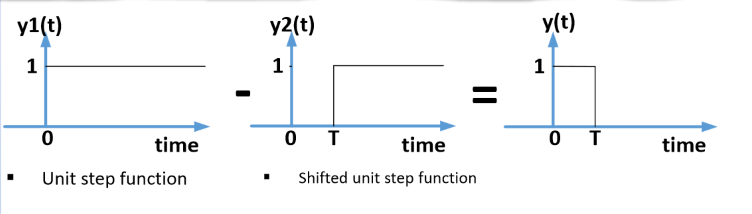

对其进行拉普拉斯变换：
\[ZOH(s)=\frac{1-e^{-Ts}}{s}\]

在数字控制系统中，零阶保持器可以将数字信号在每个抽样时刻保持这个抽样值并持续抽样周期\(T\)时长来实现数字信号到模拟信号的转换。

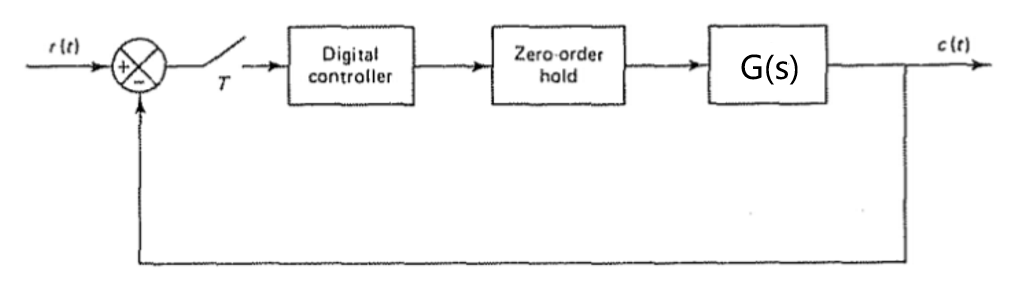
则整个系统的传输方程：
\[G_{ZA}(s)=ZOH(s)G(s)\]

如果零阶保持器和被控对象看做一个整体，对其进行z变换（即将整个系统放在z域中查看），得到：
\[G_{ZA}(z)=\frac{z-1}{z}𝒵[\frac{G(s)}{s}]\] \(𝒵[⋅]\)表示z变换。
上述公式称为零阶保持器的离散化公式。

级联系统分析

如果每个子系统分别采样(模数转换)后级联，那么系统的传递函数可以表示为：
\[G(z)=𝒵[G_1(s)]𝒵[G_2(s)]=G_1(z)G_2(z)\]

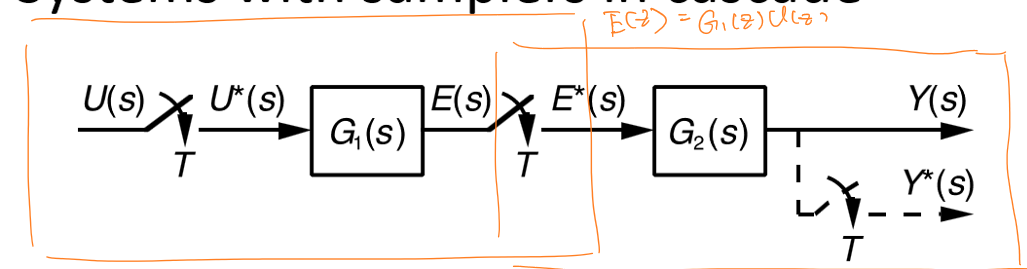
如果每个子系统先级联，最后整个做采样（模数转换），那么系统的传递函数可以表示为：
\[G(z)=𝒵[G_1(s)G_2(s)]\]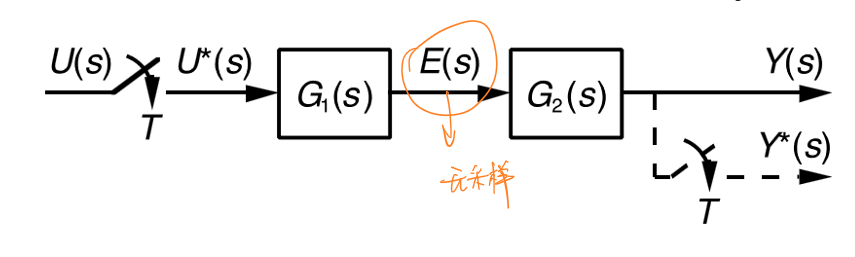

数字控制系统的分析

差分方程

数字控制系统中可以使用差分方程描述系统的特性：
\[∑b_ky(n+k)=∑a_kx(n+k)\]

需要注意系统的初始条件，如果规定了系统的初始条件：\(y(0)≠0\)、\(y(1)≠0\)，则应当利用z变换的时移性质：
\[Z[f(k+1)]=zF(z)-zf(0)\] \[Z[f(k+n)]=zF(z)-z^nf(0)-∑_{k=1}z^{n-k}f(k)\]

对差分方程两边做z变换，整理可以得到系统的闭环传递函数：
\[TF_{cl}(z)=\frac{Y(z)}{X(z)}\]

系统类型

对于数字控制系统，其开环传递函数可以表示为：
\[\frac{1}{(z-1)^N}\frac{B(z)}{A(z)}\] 以\((z-1)^N\)中\(N\)对其进行分类：\(N=0、1、2\)时，称系统分别为0/1/2型系统。
不同类型的系统在不同输入时，其瞬态响应的表现是不同的。

系统的瞬态分析

数字控制系统的瞬态中同样有设置时间、峰值时间、上升时间、滞后时间、过冲率等指标，其定义与模拟控制系统的瞬态分析相同。

稳态误差

和模拟控制系统一样，定义数字系统的稳态误差为：
\[e_{ss}=1-\lim_{z→1}(z-1)Y(z)=1-\lim_{z→1}(z-1)TF_{cl}(z)U(z)\] \(TF_{cl}(z)\)是系统的闭环传递函数。

同样地，可以根据系统输入为阶跃序列、斜坡序列、圆锥序列时，其稳态误差是：

系统类型	位置误差 \(r(n)=1\)	速度误差 \(r(n)=n\)	加速度误差 \(r(n)=\frac{1}{2}n^2\)
0型	\(\frac{1}{1+K_p}\)	\(∞\)	\(∞\)
I型	\(0\)	\(\frac{1}{K_v}\)	\(∞\)
II型	\(0\)	\(0\)	\(\frac{1}{K_a}\)

其中的静态位置误差常数\(K_p\)： \[K_p=\lim_{z→1}G(z)H(z)\] 静态速度误差常数：
\[K_v=\lim_{z→1}\frac{(1-z^{-1})G(z)H(z)}{T}\] 静态加速度误差常数：
\[K_a=\lim_{z→1}\frac{(1-z^{-1})^2G(z)H(z)}{T^2}\]