12. 数字控制稳定性
本文最后更新于 2025年6月4日 晚上
数字控制系统稳定性
模拟系统的稳定性
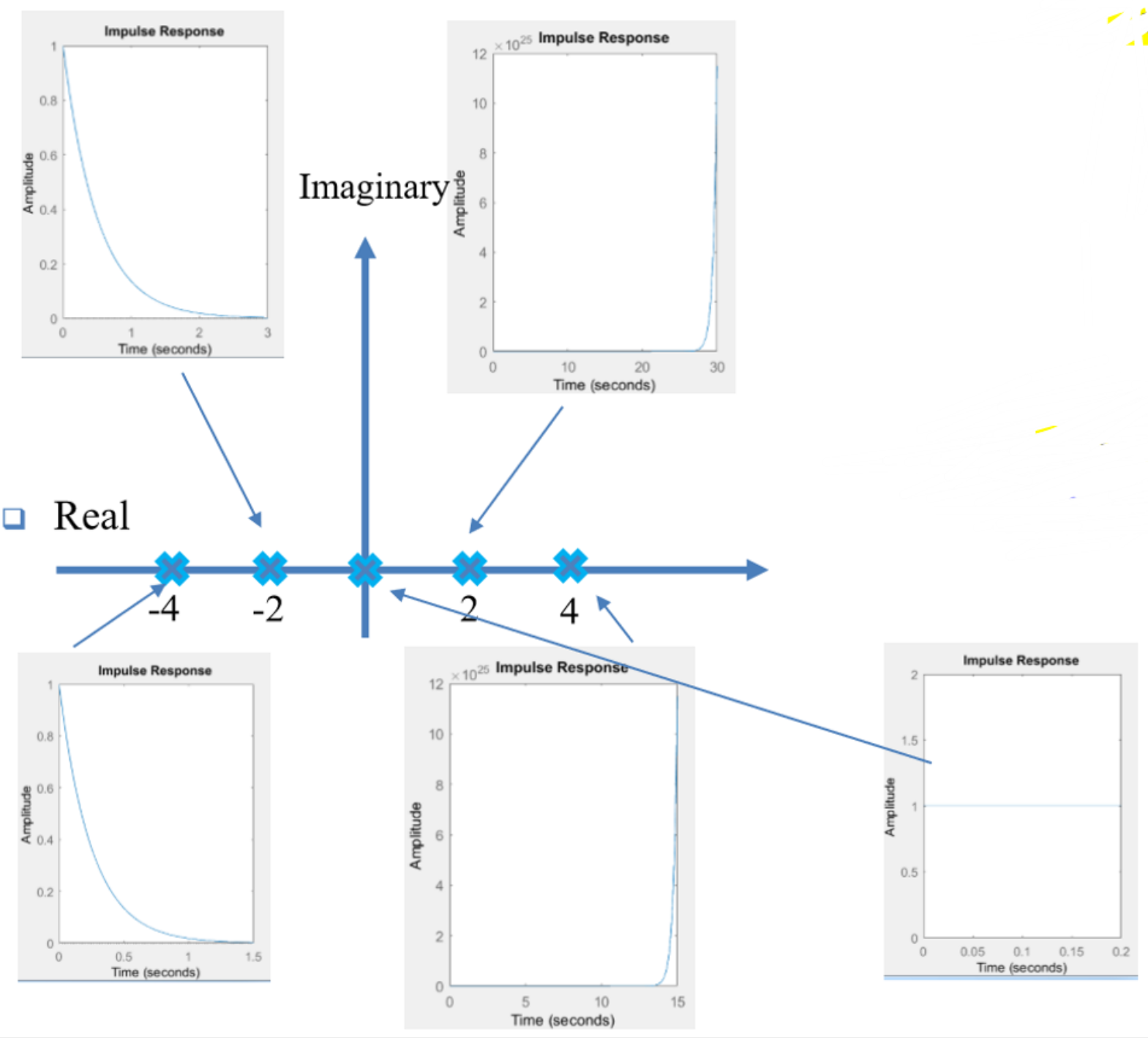
在模拟系统中,通过测试可以发现一阶系统极点在s域的位置与其系统特性存在如下关系:
- 极点在实轴、左半轴的系统:
系统响应以指数形式下降,且极点越远离虚轴下降速度越快。
- 极点在实轴、右半轴的系统:
系统响应以指数形式上升,且极点越远离虚轴上升速度越快。
- 极点在原点的系统:
系统响应是单位阶跃响应。
- 极点在虚轴的系统:
产生稳定的正弦振荡。
具有共轭复根极点的系统,其实部会影响系统响应的指数变化,而虚部则会影响其振荡频率。
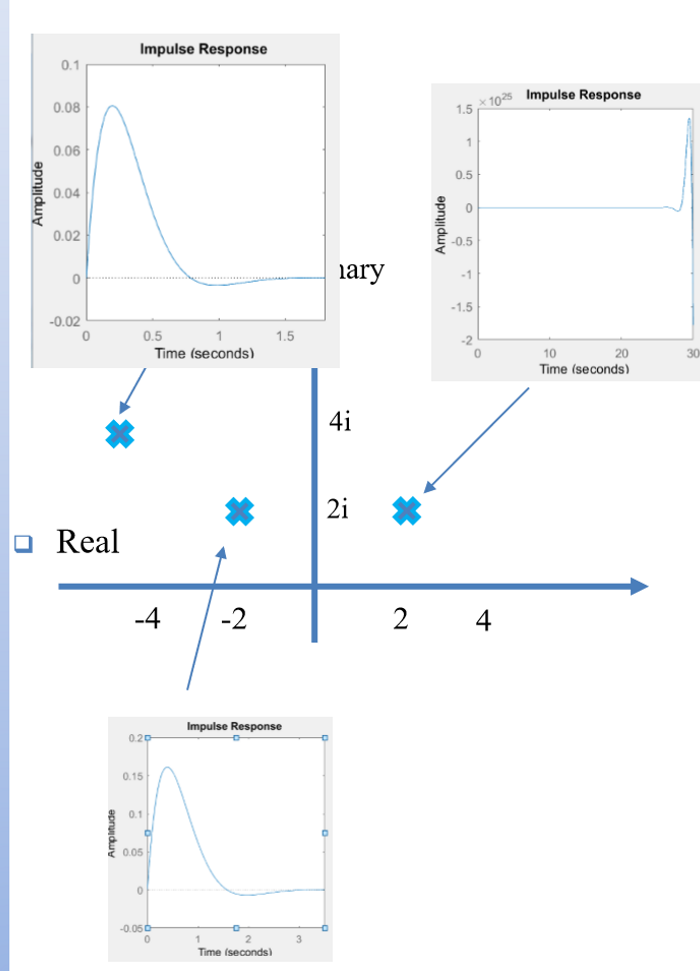
可以得出结论:
在模拟系统中,如果系统极点全部位于\(s\)域左半平面,那么系统稳定。 要想知道如何判定一个数字系统是否稳定,那么需要知道模拟系统\(s\)域和数字系统\(z\)域之间的映射关系。
s域到z域的映射
根据\(z\)变换的定义和拉普拉斯变换的定义:
\[z=e^{Ts}\] \[s=σ+jω\] 有:
\[z=e^{σT}e^{jωT}\] 令\(r=e^{σT}\),\(θ=ωT\),将其极坐标化:
\[z=re^{jωT}=re^{j∠θ}\] 那么有如图所示的对应关系:
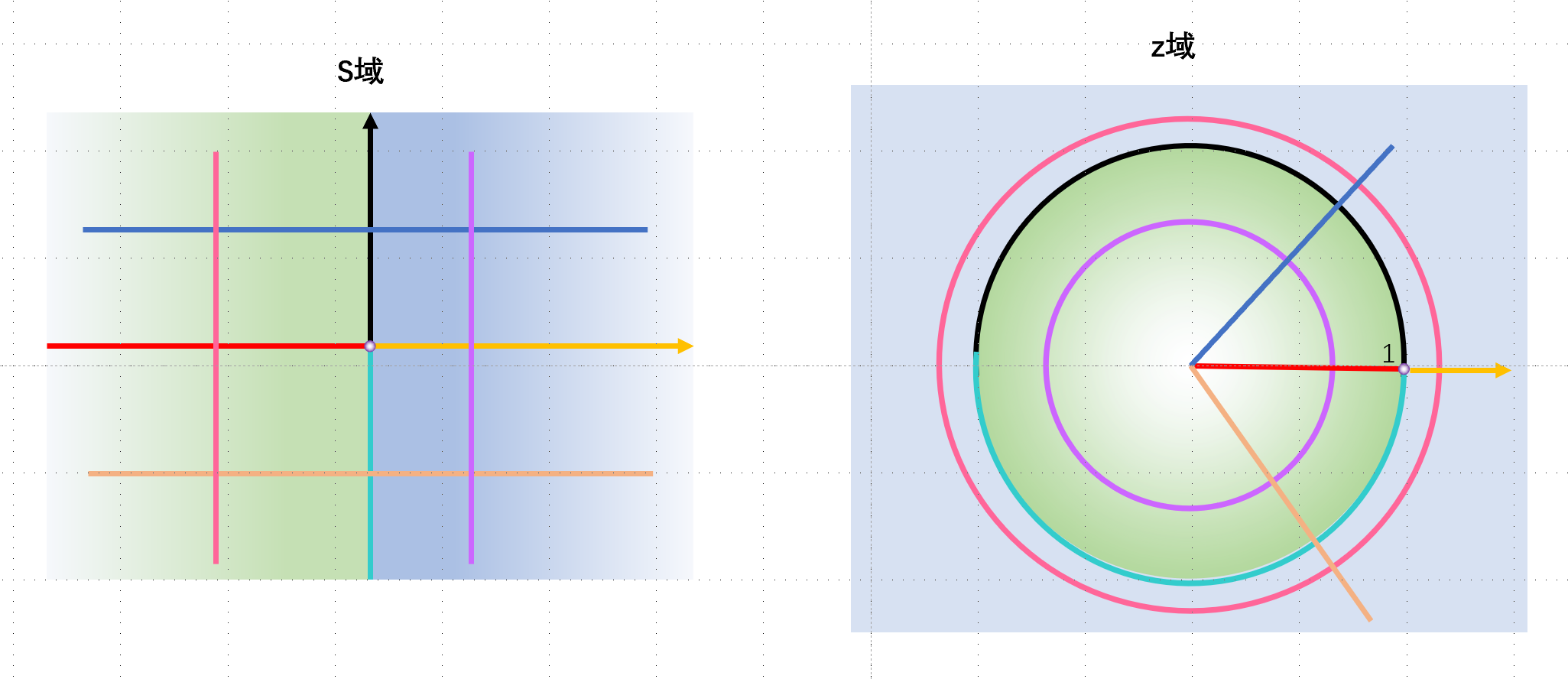
| s域 | z域 |
|---|---|
| (0,0) | (1,0) |
| 虚轴正半轴 | 单位圆上半部分 |
| 虚轴负半轴 | 单位圆下半部分 |
| 左半平面 | 单位圆内的部分 |
| 右半平面 | 单位圆外的部分 |
数字系统的稳定性
已知s域中如果系统的极点全部位于s域左半平面时,系统稳定。根据s域到z域的映射,不难得出结论:
对于数字系统,如果其所有极点全部位于z域单位圆内,则系统是稳定的。
且极点位于z域内其他位置时的系统响应形状可以通过寻找对应在s域的位置,对极点在这个位置上的系统响应进行采样和量化即可得到对应在z域的系统响应形状。
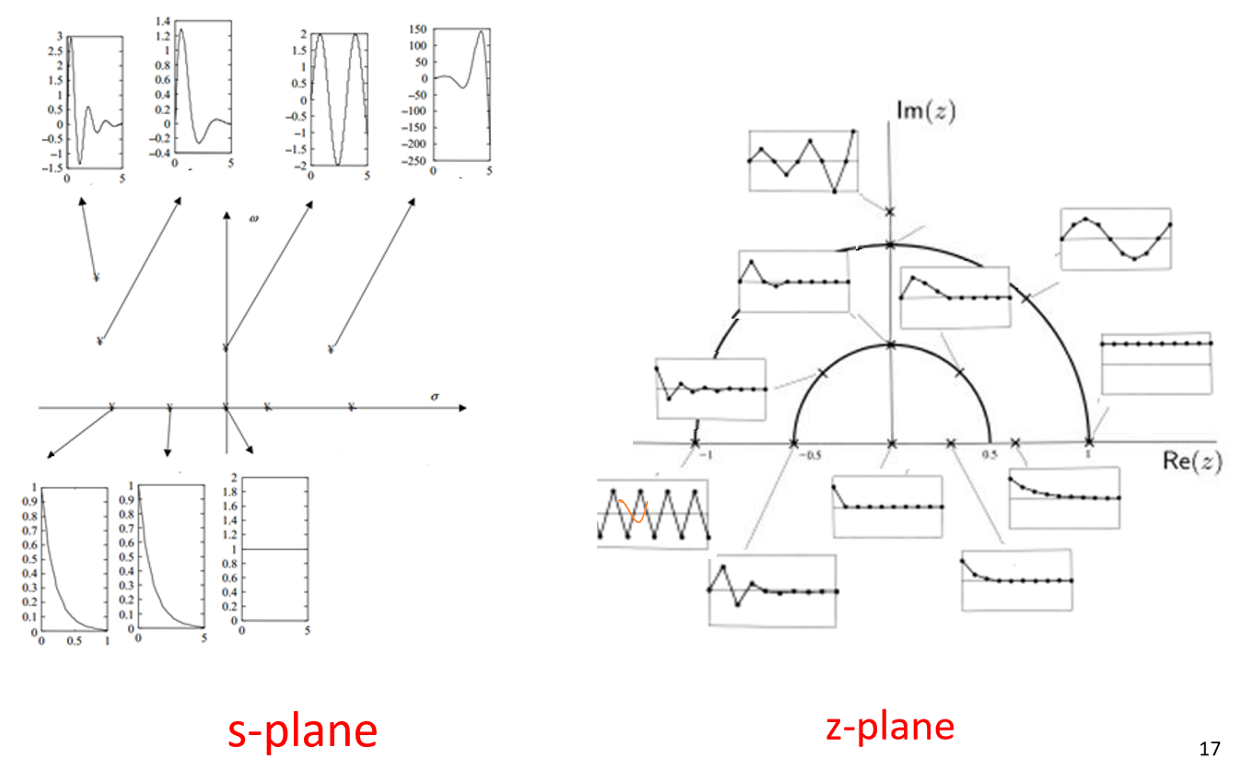
数字系统的稳定性测试
虽然已知数字系统稳定性的条件,但是对于某些高阶复杂的特征方程,无法直接使用求根公式或者因式分解来找到具体的极点位置,因此需要其他的数学方法帮助判断在已知特征方程的情况下,系统是否稳定。
劳斯判据
劳斯判据不能直接应用在z域数字系统上,因此需要通过某种方法将z域变换到连续域上,这种方法是双线性变换(bilinear transofrmation)。
在双线性变换中,定义:
\[w=σ+jω\] \[z=\frac{w+1}{w-1}\] 根据z的模\(|z|\)与1之间的关系也可以类似地得到一个z域和w域之间的区域映射关系。简单来说,z域单位圆内的部分被映射在了w域虚轴左半轴。
虽然这样的映射关系非常类似z域与s域之间的区域映射关系,但是w域和s域之间由于线性映射\(z=\frac{w+1}{w-1}\)和非线性映射\(z=ln(s)\)的区别,因此w域和s域仍然是不同的。
经过双线性变换之后的特征方程就可以使用劳斯判据对其进行稳定性测试。
朱利判据
朱利判据是一种对数字系统的稳定性判据,相比于需要先连续化特征方程的劳斯判据,朱利判据可以直接判定数字系统是否稳定。
具体而言,对于一个\(n\)阶数字系统的特征多项式:
\[F(z)=∑_{k=0}^na_{n-k}z^{n-k}\] 其稳定的必要条件是:
\[F(1)>0\] \[(-1)^nF(-1)>0\]
系统稳定的充分条件为:
将特征多项式系数按照如下的朱利表进行排列:

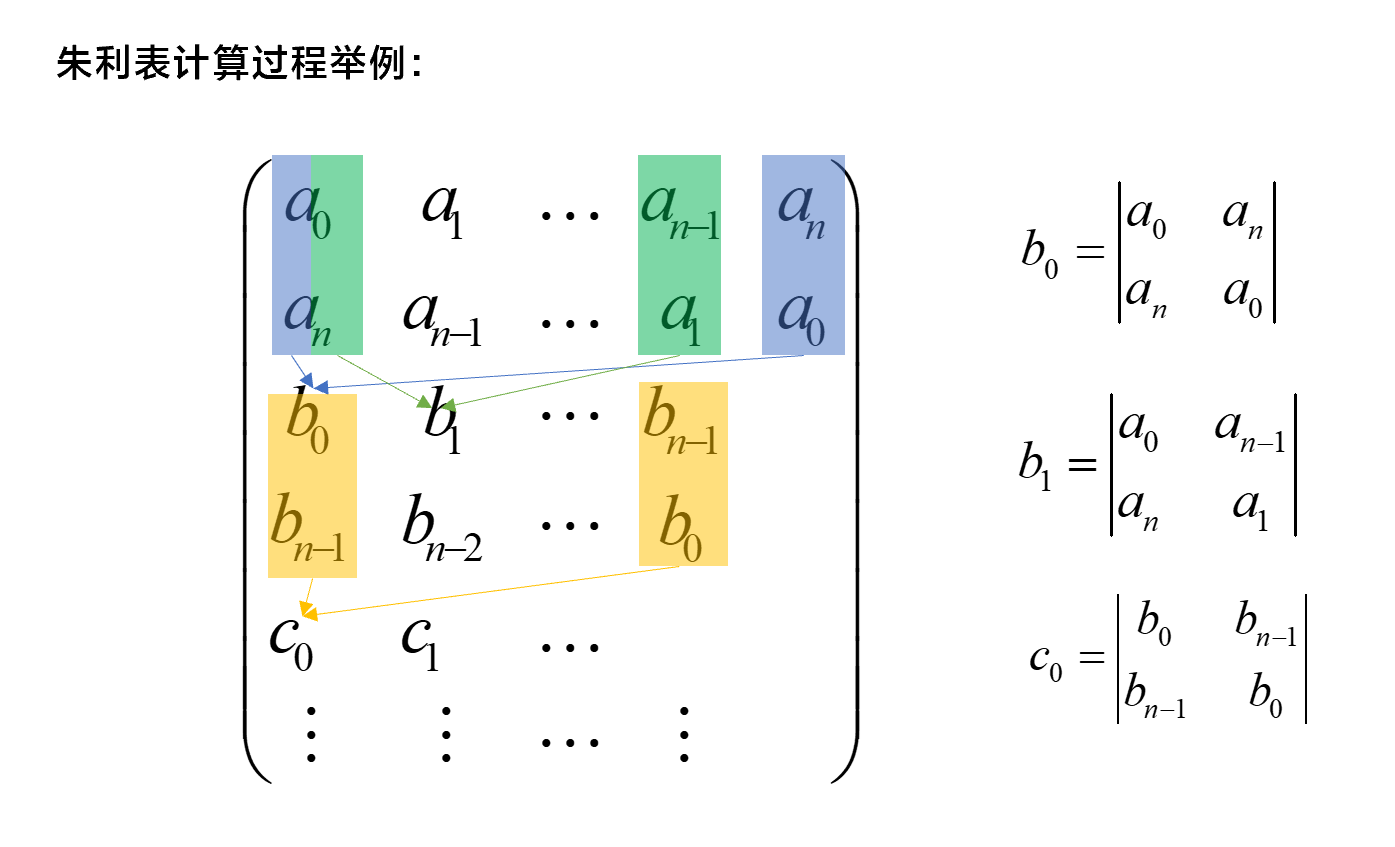
排列后的系数满足:
\[\begin{cases}
|a_0|<a_n\\
|b_0|>|b_{n-1}|\\
|c_0|>|c_{n-2}|\\
⋮
\end{cases}\] 一共\(n-1\)个条件。
对于数字系统,其特征多项式需要同时满足朱利判据中的充分条件和必要条件,该数字系统是稳定的。