13. 根轨迹图·采样周期的影响
本文最后更新于 2025年6月4日 晚上
根轨迹图·采样周期的影响
为了更好的研究开环传递函数\(G(s)H(s)\)或\(G(z)H(z)\)对反馈系统的影响,用根轨迹图(Root locus diagram)来表现对系统使用增益控制器时,根据系统闭环传递函数的极点在s域/z域中随着比例控制器的增益的变化情况来得到系统稳定性和受阻尼情况的改变情况。
简单来说,
- 根据根轨迹图可以发现系统在不稳定/稳定/临界稳定条件下时,所对应的比例控制器增益(范围),从而设置合适的增益,使得系统稳定/不稳定/临界稳定。
- 根据根轨迹图可以发现随着增益的变化系统受到阻尼的变化情况,从而可以根据设计要求的系统阻尼情况(过阻尼/临界阻尼/欠阻尼/无阻尼)来选择合适的增益。
根轨迹图的绘制方法
通过闭环传递函数绘制
通过闭环传递函数得到根轨迹图的步骤:
- 在系统前馈中增加一个增益为\(K\)的比例控制器,通过闭环传递函数的特征方程解出s与\(K\)之间的关系。
如果原来的闭环传递函数为:\(TF_{cl}(s)=\frac{G(s)}{1+G(s)H(s)}\),那么增加了比例控制器的闭环传递函数为:\(TF_{cl}(s)=\frac{KG(s)}{1+KG(s)H(s)}\)
- 找到系统的特征方程\(1+KG(s)H(s)=0\),并解出零点,在s域中标出零点。
- 在s域中标出极点,即\(K=0\)的位置。
- 增加K的值,在S域中标出一系列的s的位置,并以(\(K=x\))在每个点上方进行标注。
- 判断\(k→∞\)时,s的移动方向,并用箭头标注。
通过开环传递函数绘制
通过开环传递函数\(G(s)H(s)\)直接绘制根轨迹遵循如下规则:
根轨迹的分支数
根轨迹的分支数量是开环极点数\(n\)和开环零点数\(m\)中的最大值\(max(m,n)\)。
根轨迹的起点和终点
根轨迹的起点只能是极点,而终点要么是零点要么是无穷远处。
如果开环零点数等于开环极点数,根轨迹始于开环极点,终于其左边相邻的开环零点。
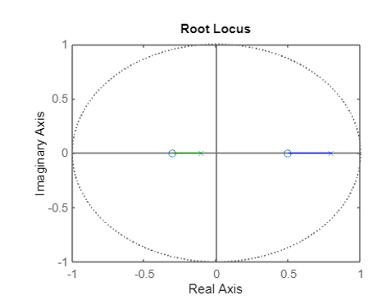
如果开环零点数小于开环极点数,那么有\(n-m\)调根轨迹终止于无穷远处。
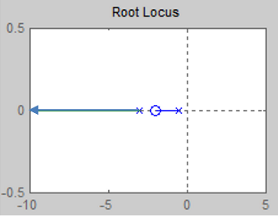
实轴上的根轨迹
实轴上的某一区域,若其右边开环实数零极点个数之和为奇数,则该轨迹是根轨迹。或者描述为:将零极点从大到小编号为(1,2,3…),实轴上第奇数个零极点左边的部分是根轨迹。
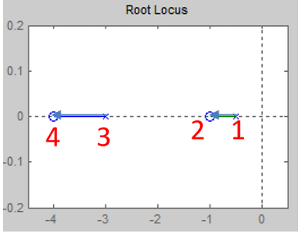
进入实轴的点(称为进入点(break-in point))是函数\(-\frac{A(z)}{B(z)},G(z)H(z)=\frac{KB(z)}{A(z)}\)的正极大值点,离开实轴的点(称为离开点(breakaway point))是函数\(-\frac{A(z)}{B(z)},G(z)H(z)=\frac{KB(z)}{A(z)}\)的正极小值点。
两个根轨迹在实轴上相遇后立即分离的点称为和分离点,在和分离点后,两根根轨迹会向对向偏转90°。其中,起点值较大的根轨迹向上偏转,起点值较小的根轨迹向下偏转。
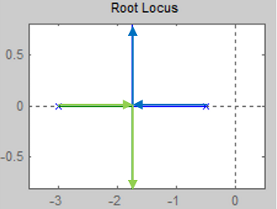
复根
如果有复根出现,则一定是共轭成对出现的。
不重叠
在任何时候,同一支根轨迹分支不会与自身重叠。
根轨迹图与数字系统特性
对于数字系统\(\frac{G(z)}{1+G(z)H(z)}\),再加入比例控制器后,其闭环传递函数写作\(\frac{KG(z)}{1+KG(z)H(z)}\),此时的特征方程为:
\[1+KG(z)H(z)=0\]
稳定最大增益
根轨迹上的稳定最大增益出现在有重根的位置。对于二阶数字系统,对应特征方程的\(Δ=0\)时对应的增益\(K\)最大。
临界稳定
对数字系统,根轨迹上与单位圆的交点对应系统处于临界稳定状态。
- 当根轨迹从实轴离开单位圆时,此时对应的极点应当为\(z=-1\)。
- 当根轨迹从z域上其他地方离开单位圆时,有如下求此时系统极点的方法:
对于二阶数字系统,其特征方程可以写作:
\[az^2+bz+c=0\] 根据求根公式,有\(z=\frac{-b±\sqrt{b^2-4ac}}{2a}=\frac{-b±\sqrt{(-1)^2×(b^2-4ac)}}{2a}\),有:
\[z=-\frac{b}{2a}±i\frac{\sqrt{4ac-b^2}}{2a}\] \[|z|=\frac{c}{a}\] 当系统处于临界稳定条件下时,\(z\)的模长应当为单位圆半径1,有:
\[|z|=\frac{c}{a}=1\]
将临界稳定时系统的极点\(z\)带入含有比例增益\(K\)的特征方程中,即可求得临界稳定时的比例增益\(K_{crs}\)。
临界阻尼
根轨迹和系统的受阻尼状态有如下关系:
- 当根轨迹位于实轴时,特征方程的\(Δ>0\),对应\(ζ>1\),系统过阻尼。
- 当根轨迹离开实轴时,特征方程的\(Δ>=00\),对应\(ζ=1\),系统处于临界阻尼状态。
- 当根轨迹不在虚轴时,特征方程的\(Δ<0\),对应\(0<ζ<1\),系统欠阻尼。
当数字系统的根轨迹离开实轴或者进入实轴时,系统处于临界阻尼状态。要系统的临界阻尼状态对应的极点即是离开点和进入点,其求法是化简特征方程,得到比例增益关于z的函数\(K(z)\),对其求导且令其为0: \[\frac{dK}{dz}=0\] 其中微分方程的解中较大的值是根轨迹的离开点,较小的值是根轨迹的进入点。
将临界阻尼时系统的极点\(z\)带入含有比例增益\(K\)的特征方程中,即可求得临界稳定时的比例增益\(K_{crd}\)。
采样周期对系统性质的影响
采样周期对稳定性的影响
零阶保持器可以将数字信号在每个抽样时刻保持这个抽样值并持续抽样周期\(T\)时长来实现数字信号到模拟信号的转换。零阶保持器的\(z\)域传递函数表示为:
\[G(z)=\frac{z-1}{z}Z[\frac{G(s)}{s}]\] 其中\(Z[\frac{G(s)}{s}]\)中含有抽样周期\(T\).
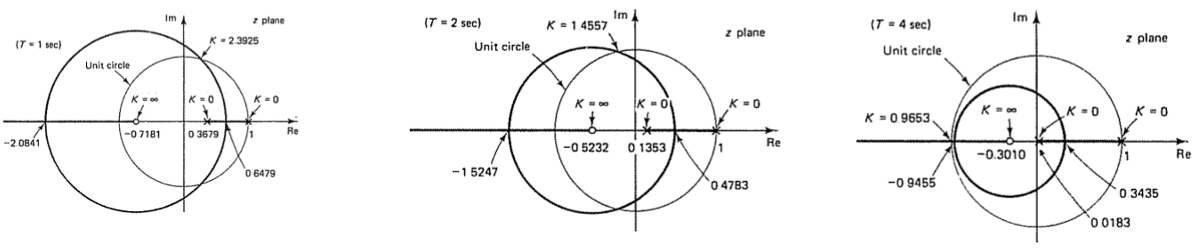
此时改变\(T\)的值,并研究不同\(T\)下的根轨迹方程,以及\(K_{crs}\).可以得到结论。
采样周期可以影响数字系统的稳定性:随着采样周期的增大,临界稳定时的比例增益\(K_{crs}\)越小,表明系统越不稳定。
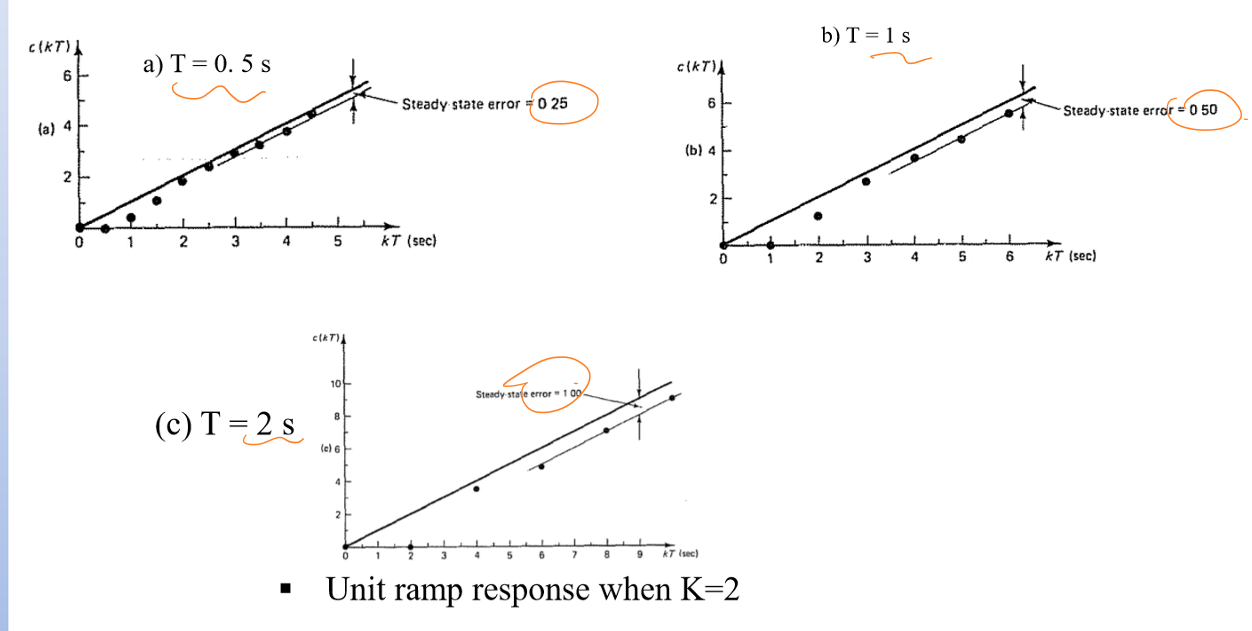
采样周期对稳态误差的影响
稳态误差可以通过先求静态速度误差常数,再使用\(e_{ss}=\frac{1}{K_v}\)得到。
可以发现,随着采样周期的增加,稳态误差也相应的增加。
采样周期对受阻尼情况的影响
同样地,改变\(T\)的值,并研究不同\(T\)下的根轨迹方程,以及阶跃响应.可以得到结论。
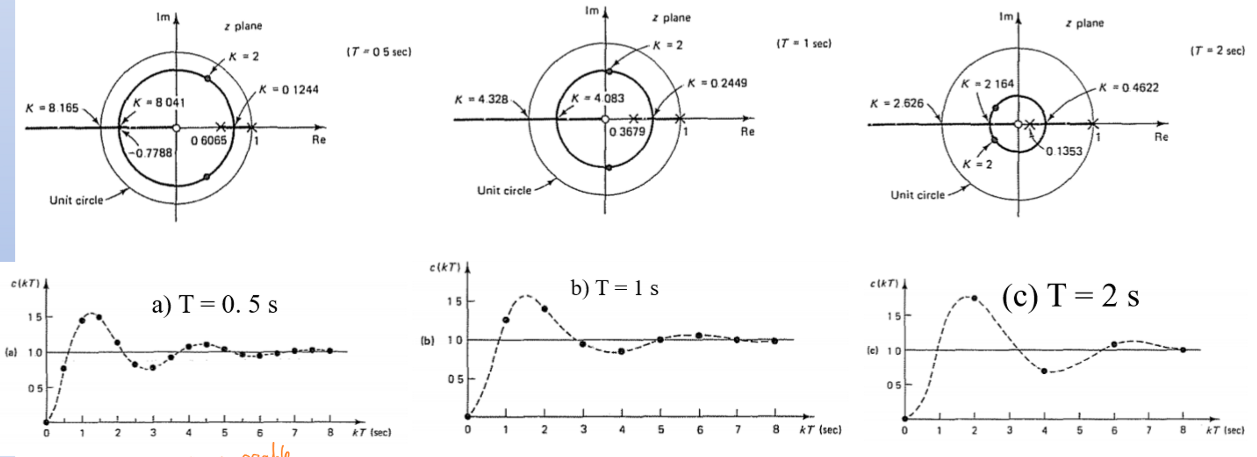
如果采样频率不够高,那么阶跃响应的过冲率会高于通过\(ζ\)预测的过冲率。
采样周期的设置
可以发现,采样周期的设置会对系统的稳定性、稳态误差以及瞬态响应的表现都有影响。
采样周期设置一般需要遵循:
- 奈奎斯特采样定律,即\(\frac{1}{T}<2f_H\)
- 对于过阻尼系统,满足在峰值时间\(t_p\)内需要8到10次采样。
- 对于欠阻尼系统,满足在一振荡周期内\(T\)内需要8到10次采样。
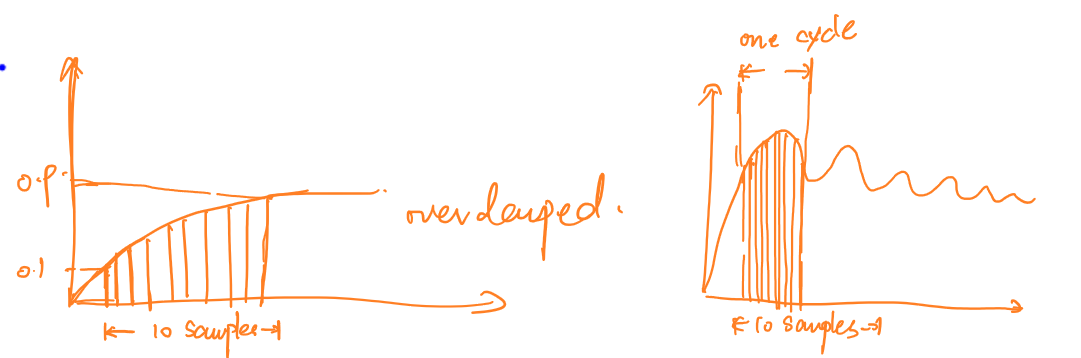
- 采样器的硬件实施能力。