14. 数字PID控制器和补偿器及其设计
本文最后更新于 2025年6月4日 晚上
数字PID控制器和补偿器及其设计
数字PID控制器的设计思路是首先根据设计要求设计出模拟的PID控制器,再使用一定的离散化(Discretisation)方法使其转变为数字PID控制器。
数字控制器在整个数字控制系统中的位置如下:
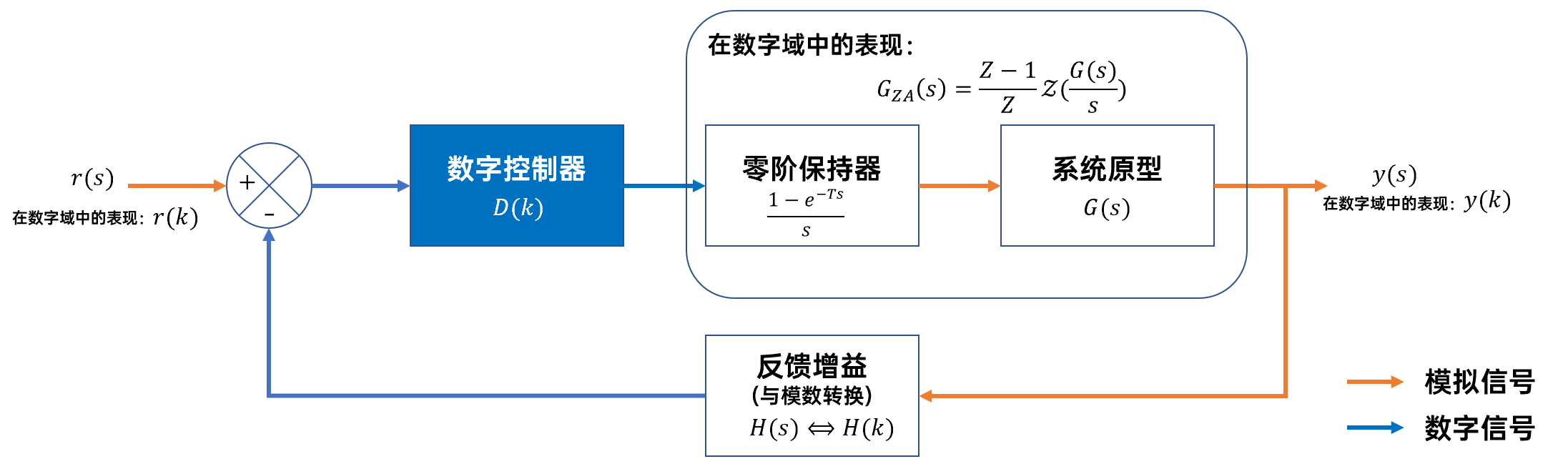
尽管系统中存在大量的模拟环节和模拟信号,对于整个数字系统的分析和设计需要以数字控制器为准,即在数字控制器设计时,应当将整个系统放在Z域中考虑。
离散化方法
所谓离散化是指使用一定的数学映射方法将s域的表示映射到z域上。常见的离散化方法有:
- 前向欧拉法(Euler’s forward method)
- 后向欧拉法(Euler’s backward method)
- 双线性法/塔斯汀法(Tustin’s method/bilinear transformation)
- 零阶保持器的离散化公式
前向欧拉法
前项欧拉法中使用采样序列的第\(k+1\)项和第\(k\)项的差来近似响应的微分:
\[\frac{dy}{dt}≈\frac{dy}{dk}=\frac{1}{T}[y(k+1)-y(k)]\]
对上述表达式左侧做拉普拉斯变换,右侧做z变换,即可得到s域到z域的映射关系:
\[sY(s)→\frac{1}{T}[zY(z)-Y(z)]\] \[sY(s)→\frac{1}{T}[z-1]Y(z)\] 由于\(Y(s)→Y(z)\),有映射律: \[s→\frac{1}{T}(z-1)\] 同理可以得到二阶响应的近似:
\[\frac{d\dot{y}}{dt}≈\frac{d\dot{y}}{dk}=\frac{1}{T}[\dot{y}(k+1)-\dot{y}(k)]\]
同理推出:
\[\ddot{y}(k)≈\frac{1}{T^2}[y(k+2)-2y(k+1)+y(k)]\]
后向欧拉法
后项欧拉法中使用采样序列的第\(k\)项和第\(k-1\)项的差来近似响应的微分:
\[\frac{dy}{dt}≈\frac{dy}{dk}=\frac{1}{T}[y(k)-y(k-1)]\]
同理,经过拉普拉斯变换和z变换后,得到s到z的映射律为:
\[s→\frac{1}{T}\frac{z-1}{z}\] 其二阶响应映射为:
\[\ddot{y}(k)≈\frac{1}{T^2}[y(k+2)-2y(k+1)+y(k)]\]
双线性法
双线性变换由\(z=e^{Ts}\)使用泰勒公式对其展开:
\[z=\frac{e^{\frac{sT}{2}}}{e^{-\frac{sT}{2}}}≈\frac{1+\frac{sT}{2}}{1-\frac{sT}{2}}\] 得到映射律:
\[s→\frac{2}{T}\frac{z-1}{z+1}\]
零阶保持器的离散化公式
如果零阶保持器和被控对象看做一个整体,对其进行z变换(即将整个系统放在z域中查看),得到:
\[G_{ZA}(z)=\frac{z-1}{z}𝒵[\frac{G(s)}{s}]\] \(𝒵[⋅]\)表示z变换。
上述公式称为零阶保持器的离散化公式。
性能分析
s域左半平面在上述三种映射律下的映射情况如下图所示:
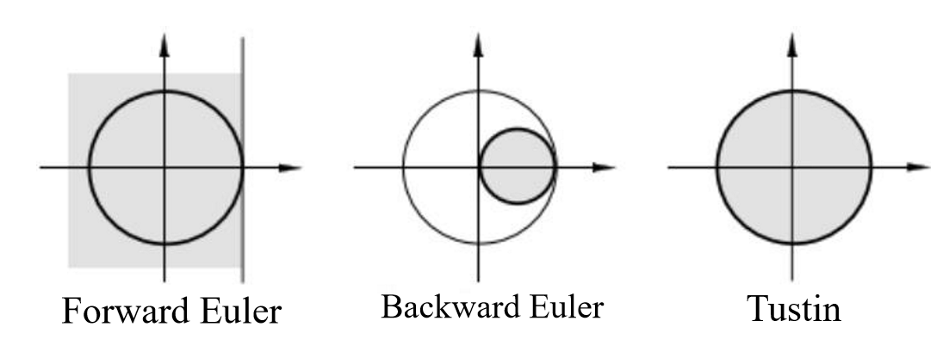
可以发现,前向欧拉法将某些s域中的稳定系统映射到了z域中不稳定的部分。
后向欧拉法将s域中的稳定系统和部分不稳定系统都映射到了z域中稳定的部分。
使用双线性法,系统的稳定性在映射前后不变。
使用MATLAB 对连续系统离散化
在MATLAB中,可以使用函数c2d(sys,ts,'method')对一个连续系统sys离散化,sys是连续系统的传递函数,ts是离散化所指定的采样时间,method是所采用的离散化方法:zoh或z表示零阶保持器,tustin表示双线性变换。
数字化的PID控制器
加州大学伯克利分校:数字PID控制器设计 https://msc.berkeley.edu/assets/files/PID/modernPID4-digitalPID.pdf
数字化的PID控制器的性质和模拟PID控制器的性质相同,但是其传递函数被离散化到了z域。数字化的PID控制器的传递函数如下表所示:
| 控制器类型 | 传递函数 |
|---|---|
| P控制器 | \(G_D(z)=K_p\) |
| I控制器 | \(G_D(z)=K_iT\frac{z}{z-1}\) |
| D控制器 | \(G_D(z)=\frac{K_d}{T}\frac{z-1}{z}\) |
| PI控制器 | \(G_D(z)=K_p+K_i\frac{z}{z-1}=\frac{(K_p+K_iT)(z-\frac{K_p}{K_p+K_iT})}{z-1}\) |
| PD控制器 | \(G_D(z)=K_p+\frac{K_d}{T}\frac{z-1}{z}=\frac{(K_p+\frac{K_d}{T})(z-\frac{\frac{K_d}{T}}{K_p+\frac{K_d}{T}})}{z}\) |
| PID控制器 | \(G_D(z)=\frac{K_2z^2+K_1z+K_0}{z(z-1)},K_p=-K_1-2K_0,K_i=\frac{K_0+K_1+K_2}{T},K_d=K_0T\) |
数字超前/滞后补偿器设计
数字控制器设计的思路有两种,其一是先设计模拟控制器,然后根据离散化方法将其转化为数字控制器。因为这种方法简单,在实际设计中通常选择这种方法,但是需要选择合适的T(通常是\(T=0.1t_s\))。在采样周期\(T\)规定的情况下,要想精确地设计数字控制器,则需要直接在z域中进行设计。
模拟控制器数字化
- 根据设计要求,利用模拟PID控制器的设计方法(比如齐格勒-尼科尔斯方法)设计出模拟控制器\(D(s)\)。
- 使用离散化方法对设计出的模拟控制器\(D(s)\)进行离散化得到\(D(z)\)。
如果零阶保持器和系统原型的离散化写作\(G_{ZA}(z)\),设计好的数字控制系统的闭环传递函数为:
\[TF_{cl}(z)=\frac{D(z)G_{ZA}(z)}{1+D(z)G_{ZA}(z)}\] 找到其特征多项式\(1+D(z)G_{ZA}(z)\)后可以使用朱利判据测试其稳定性。
如果系统稳定,可以通过\(e_{ss}=1-\lim_{z→1}(z-1)Y(z)\)找到其稳态误差。
根轨迹方法
根轨迹方法是一种在Z域中进行直接设计的方法。
理论基础
- 理论一
根据z变换中的定义:\(s=σ+jω\),\(z=e^{sT}=e^{T(σ+jω)}\),有z域上任意一极点\(z\):
\[|z|=e^{-Tσ}=e^{-Tζω_n}\] \[∠z=Tω_d=\frac{2πω_d}{ω_s}\] 其中,采样次数为:
\[n_s=\frac{ω_s}{ω_d}\] 工程设计中通常需要满足\(8<n_s<10\)。
- 理论二
对于数字系统的特征方程\(L(z)+1=0\),有\(L(z)=-1\),此时可以将\(L(z)\)分解为幅度和角度,那么有:
\[∠L(z)=∑∠zero-∑∠pole=±180°(2k+1),k=0,1,2,...\] \[|L(z)|=1\] 因此,数字系统中某一极点与其他所有零极点的连线与实轴正半轴夹角的角度和应当为±180°。
设计流程
对于超前/滞后补偿器\(D(z)=K\frac{z+α}{z+β}\):
- 根据系统要求找到阻尼比\(ζ\)、固有频率\(ω_n\)、阻尼固有频率\(ω_d\),并找到设计的极点\(z\)的模长\(|z|\)和角度\(∠z\)。
- 利用\(a=|z|cos∠z,b=|z|sin∠z\)将极点表示为\(z=a+bj\)的形式,并在z域上标出位置点\(P\)。
- 将系统原型数字化,并找到系统原型的零点和极点。
- 选择\(α\)为系统原型的一个极点,实现零极点对消以简化计算。
- 将系统原型剩余的零极点与P连线的夹角利用\(arctan(\frac{y_1-y_2}{x_1-x_2})\)算出每一条连线与实轴正半轴的夹角。
- 利用\(∠β=∑∠zero-∑∠pole+180°\)找到需要增加的零点\(β\)的角度。
- 利用\(∠β=arctan(\frac{b}{a-β})\)求得需要增加的零点的具体位置\(β\)。
- 利用\(|D(z)G_{ZA}(z)|_{z=a+bj}=1\)解方程求得\(K\)。
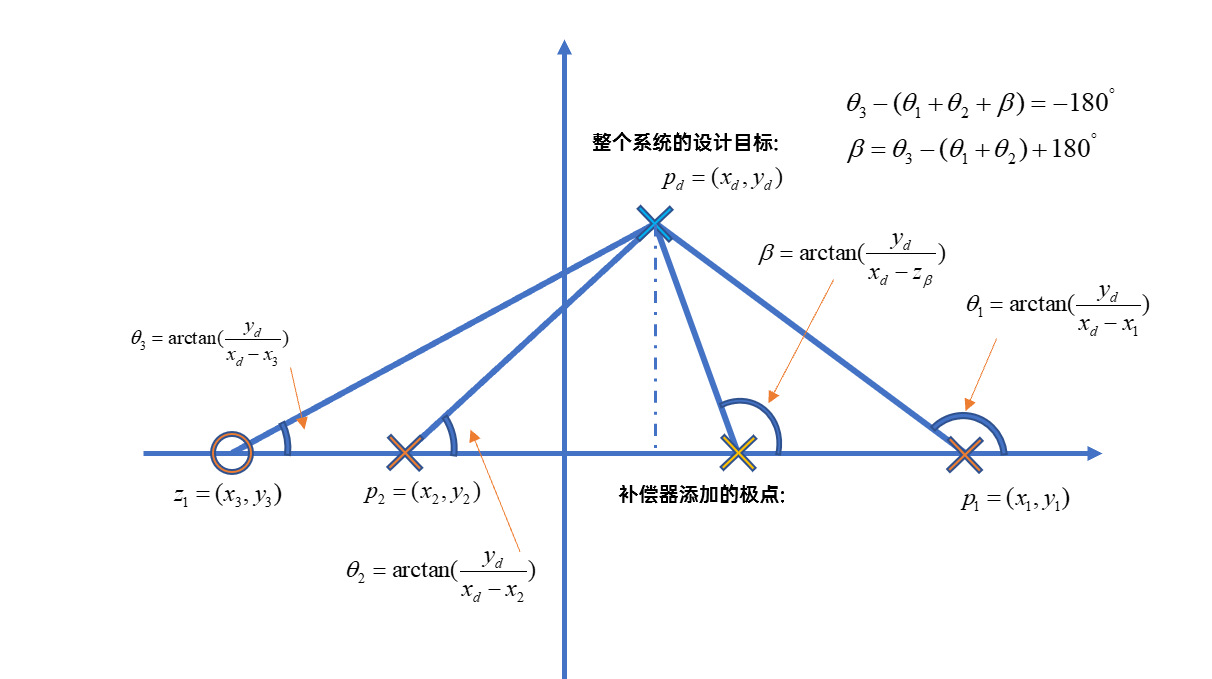
对于PID控制器也可以使用同样的设计方法对其进行设计,只是其控制器结构发生变化,由于I和D控制器均存在确定的分子分母,在利用根轨迹方法设计时还需要考虑这些确定的分子分母对系统角度的贡献:
- 对于PI控制器,其在(1,0)处贡献了一个极点。
- 对于PID控制器,其在(0,0)和(1,0)处分别贡献了一个极点。
如果零阶保持器和系统原型的离散化写作\(G_{ZA}(z)\),设计好的数字控制系统的闭环传递函数为:
\[TF_{cl}(z)=\frac{D(z)G_{ZA}(z)}{1+D(z)G_{ZA}(z)}\] 找到其特征多项式\(1+D(z)G_{ZA}(z)\)后可以使用朱利判据测试其稳定性。
如果系统稳定,可以通过\(e_{ss}=1-\lim_{z→1}(z-1)Y(z)\)或者静态误差系数找到其稳态误差。