2.金属线传输理论
本文最后更新于 2025年6月4日 晚上
金属线传输理论
传输线可以分为两大类:金属传输线和介质传输线(光纤),金属传输线中以电信号作为信息载体,本课将分析电信号在金属传输线中传输时的性质。
正弦行波的传输情况
无衰减的传输情况
金属传输线中通常采用若干相互叠加的正弦信号作为信息载体。 首先分析单个正弦波在理想金属线中的传播情况:在源点发出的一个正弦电信号可以用电压或者电流来表示:
理想金属线指:(1)无穷长的传输距离,意味着波无法到达接收端,即不会有反射波。 (2)传输线的各种物理性质是均匀的,各参考点之间没有区别。理想的平行双线中,两条线的间距始终保持不变。
\[v=Vsinωt\] 根据波理论和振动理论,源点所携带的电磁波的振动信息会向前传给传输线上的每一个“点”(类比质点,指传输线上距离非常小的一段),由于传播时延,振动信息虽然相同,但是传输线上每一个点的起振时间不同,从而相比于源点的振动,传输线上其他点的振动有相移,不难知道这个相移与传输线上该点的位置\(z\)有关。那么,传输线上某点的振动方程可以用电压表示为:
\[v=Vsin(ωt-βz)\] 其中\(β\)称为相移常数(phase change coefficient),国际标准单位为rad/m.
通过对波形的观察可以发现,\(z=nλ,n∈z^*\)位置上的点其电压的变化总是与源点相同,其相移正好为\(2π\),那么有:
\[βλ=2π\] 即,
\[β=\frac{2π}{λ}\] 从上式可以看出,\(β\)的物理意义是单位长度中存在完整波形的个数,因此\(β\)又称为波数(wave number)。
相速度和相速度
单一波形的振动信息沿着传输线传播的速度称为相速度(phase velocity),记为\(v_p\)。根据定义,在波上取两个相位相同\((ωt_1-βz_1=ωt_2-βz_2)\)的点,它们正好空间上间隔一个波长\(λ\):
\[v_p=\frac{z_2-z_1}{t_2-t_1}=\frac{λ}{T}=\frac{ω}{β}(km/s)\] 相速度的物理意义是相位信息传播的速度。
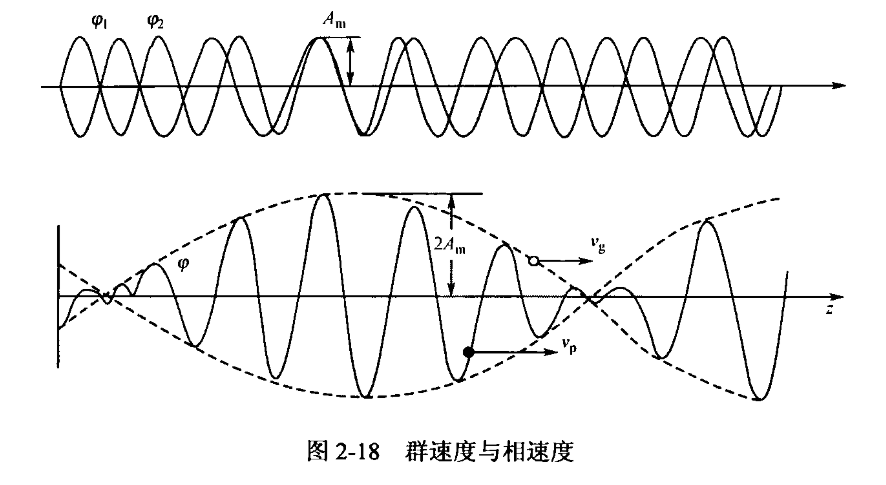
根据带宽理论,传输波形是由若干个正弦波叠加形成的包络波形,这个包络波形的相速度称为群速度(group velocity),记为\(v_g\)。
群速度表达式的推导如下:假设有两个波,其之间各种波的特性相差较小,假定其中一个波的角速度为\(ω+dω\)、波数为\(β+dβ\),另一个波的角速度为\(ω-dω\)、波数为\(β-dβ\),它们的幅值\(A_m\)相同:
\[Φ_1(t,z)=A_mcos[(ω+dω)t-(β+dβ)z]\] \[Φ_2(t,z)=A_mcos[(ω-dω)t-(β-dβ)z]\] 合成波为:
\[Φ=Φ_1(t,z)+Φ_2(t,z)=2A_mcos(tdω-zdβ)cos(ωt-βz)\] 根据群速度的定义,在合成波形上取相位相同的两点:
\[v_g=\frac{z_2-z_1}{t_2-t_1}=\frac{dz}{dt}=\frac{dω}{dβ}\] 群速度的倒数\(|\frac{dβ}{dω}|\)称为群时延(group delay)。
有衰减的传输情况
在金属传输线中,传输的衰减关于传输线距离指数增长,记这个增长率为\(α\),称为衰减参数(attenuation coefficient),其国际标准单位为Np/m.那么有:
\[v=Ve^{-αz}sin(ωt-βz)\] 可以发现,\(α\)只会影响传播过程的幅度,而\(β\)只会影响传播过程的相位。 根据复向量的定义,复数的虚部只会影响复数的相位角,实部影响复数的模长。那么将这个方程向量化,则有:
\[\mathbf{V_z}=\mathbf{V_0}e^{-αz}e^{-jβz}=\mathbf{V_0}e^{-(α+jβ)z}\] 定义\(γ=α+jβ\),称其为传播常数(propergation constant),整理得到:
\[\mathbf{V_z}=\mathbf{V_0}e^{-γz}\] 同理,传输线上任意一点的电流可以表示为:
\[\mathbf{I_z}=\mathbf{I_0}e^{-γz}\]
平行双线传输线理论
在金属传输线中,最容易对其传输特性进行分析的是平行双线传输线(twin-wire transmission line)。
平行双线传输线效应
集肤效应/趋肤效应
传输线中,随着电信号频率的上升,导体内部的电荷更倾向于从导体中心向导体表面移动,因此导体表面的电荷量上升,内部的电荷量下降,导致导体的有效导电面积下降,导体的电阻随着电信号频率的上升而升高——这样的现象称为集肤效应/趋肤效应(skin effect)。
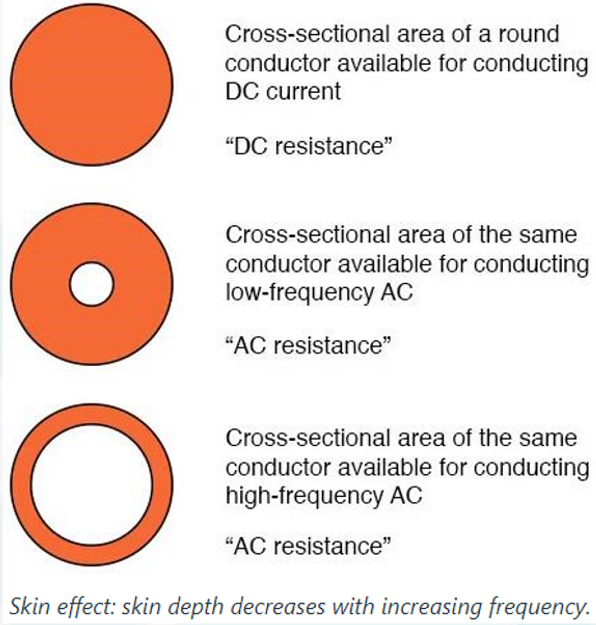
因此,利用金属传输线传输高频信号时,传输距离主要受到趋肤效应带来的能量耗散限制。
在实际应用中,话音信号300Hz-3.4kHz的传输距离在5km以内。
分布参数效应
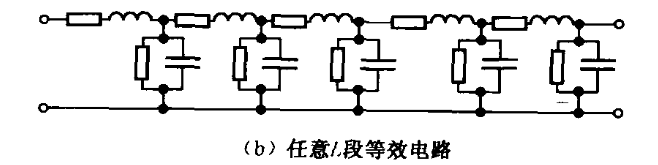
信号通过传输线时,导线周围会产生高频磁场,因此沿线各点会串联分布电感\(L\);又因为电导率有限的导线流过电流时会有集肤效应和热耗,表现为导线有串联分布的电阻\(R\);两导线间加上电压时,线间会存在高频电场,于是线间会产生并联分布电容\(C\);导线间介质非理想绝缘时存在泄漏电流,意味着导线之间有分布导纳\(G\),这就是所谓的分布参数效应。于是在研究电信号在传输线中的传输性质时,一段平行双导线可以看作是若干个串联的电阻和电感、以及若干个并联的导纳和电容,利用电路分析理论方法来分析。
当传输线的几何长度\(L\)比其上所传输的电磁波的最小波长\(λ_{min}\)还长,即\(L≥\frac{λ_{min}}{100}\)时称传输线为长线,否则为短线。
当传输线可以视为短线时,可以将这一段传输线的参数分布看做是单位的电路器件连接。
传输线分析方法有两种:利用电路分析理论方法分析和利用电磁场理论方法分析。前者需要假定各种理想情况并且设置各种条件,但是容易计算,非常便捷有效,仅适用于高频电信号和微波的低频段;后者计算复杂,但是得出结论更为精确。
电报方程
那么,在平行双线传输线上一段非常小的距离\(dz\)上的电压和电流情况如下图所示:
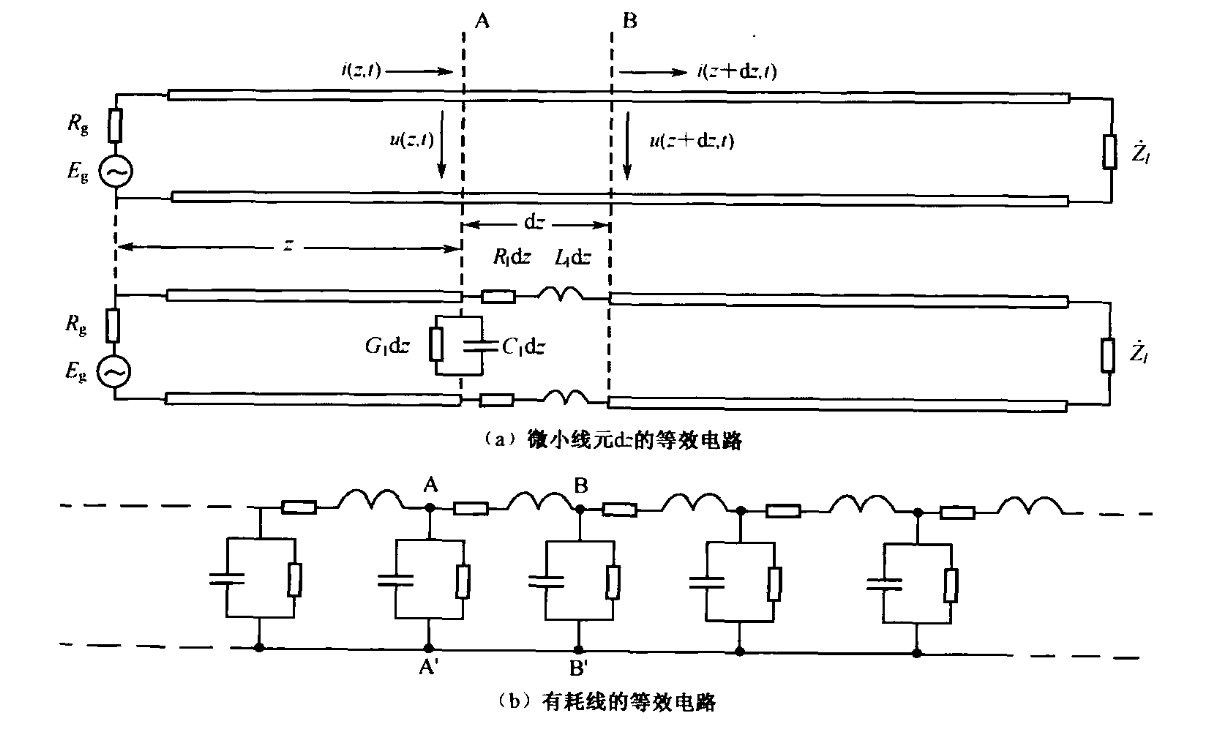
定义传输线的源点连接了一个角频率为ω的正弦信号源,此时传输线上\(t\)时刻在位置\(z\)处的电压和电流的瞬时值为\(v(z,t)=Re(\mathbf{V})=Re(V(z)e^{jωt})\),\(i(z,t)=Re(\mathbf{I})=Re(I(z)e^{jωt})\),在位置\(z+dz\)处的输出电压和电流分别为\(v(z+dz,t)\)、\(i(z+dz,t)\),通过基尔霍夫电压定律和基尔霍夫电流定律即可得到如下关系:
\[\begin{cases}
-\frac{∂v(z,t)}{∂z}=Ri(z,t)+L\frac{∂i(z,t)}{∂t}\\
-\frac{∂i(z,t)}{∂z}=Gv(z,t)+C\frac{∂v(z,t)}{∂z}\\
\end{cases}\] 该式子称为均匀传输线方程/电报方程(telegraph equation)。
在某一确定的时刻下,该式子可以改写为:
\[\begin{cases}
\frac{d}{dz}\mathbf{V}=-(R+jωL)\mathbf{I_z}\\
\frac{d}{dz}\mathbf{I}=-(G+jωC)\mathbf{V_z}\\
\end{cases}\]
具体的推理过程:Lecture 2 传输模型
特征阻抗
由\(\frac{d}{dz}\mathbf{V}=-γ\mathbf{V_z}\),有:
\[γ\mathbf{V_z}=(R+jωL)\mathbf{I_z}\] \[γ\mathbf{I_z}=-(G+jωC)\mathbf{V_z}\] 两式子相比,得到:
\[Z_0=\frac{\mathbf{V_z}}{\mathbf{I_z}}=\sqrt{\frac{R+jωL}{G+jωC}}\] \(Z_0\)表示该均匀传输线上任意一点的阻抗,称为该传输线的特征阻抗(characteristic impedance)。
传播常数
两式相乘,得到:
\[γ^2\mathbf{V_z}\mathbf{I_z}=(R+jωL)(G+jωC)\] 即:
\[γ=\sqrt{(R+jωL)(G+jωC)}\]
理想金属线传播
在理想金属线中,能量在传输线上不会有热耗,\(R=0,G=0\),此时传输线的特征阻抗为:
\[Z_0=\sqrt{\frac{L}{C}}\] 有两种情况也可以将传播情况视为理想情况:
- 在高频传输中,\(ωL>>R,ωC>>G\),此时也可以看做是低损耗的。
- 当\(\frac{R}{L}=\frac{G}{C}\)时,也可以得到\(Z_0=\sqrt{\frac{L}{C}}\),也可以看做是理想传输。
此时的传播常数为:
\[γ=jω\sqrt{LC}\]
高频金属线传播
对于高频信号:\(ωL>>R,ωC>>G\),有:
\[Z_0=\sqrt{\frac{L}{C}}\] \[γ=\frac{1}{2}(G\sqrt{\frac{L}{C}}+R\frac{C}{L})+jω\sqrt{LC}\]
传输损耗现象
色散
理想条件下,一组正弦信号的群速度\(v_g=\frac{dω}{dβ}\)应当是频率无关的。如果群速度与信号频率相关,由不同频率正弦信号组成的矩形脉冲信号在传输过程中其初始相速度不同导致合成波形在传输过程中随着时间逐渐散开,称为色散(dispersion)。
反射
双向脉冲信号的传播
在理想传输线中,两个矩形脉冲在传输线上相遇,如果两个矩形脉冲的幅度同向,则相遇时电压相加,电流相减;如果两个矩形脉冲的幅度反向,则相遇时电压相减,电流相加。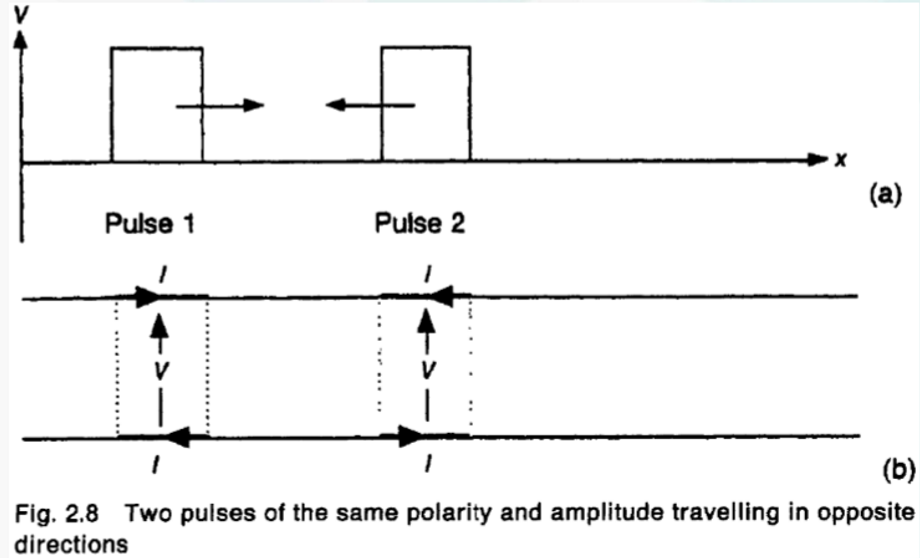
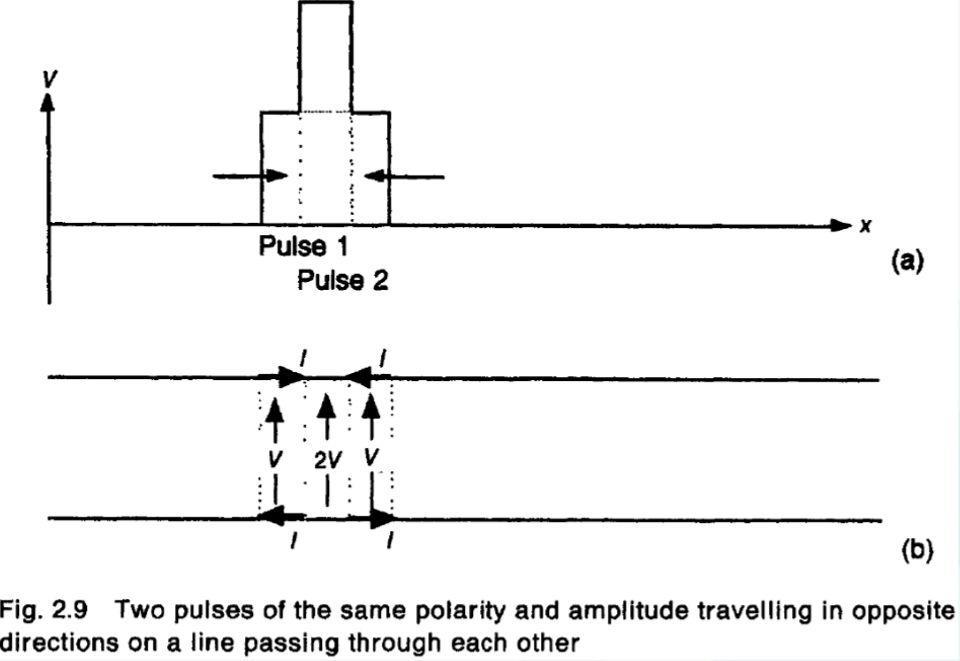
脉冲的反射
上述理论也可以应用在正弦波信号中:假设双线收端短路,那么脉冲能量无法在传输线收端被吸收,此时脉冲电压变为零,电流流经短路区后流动方向与之前相反,将流经段短路区后的电流视为反射电流,这样的反射现象是反向反射(reflection with inversion)。
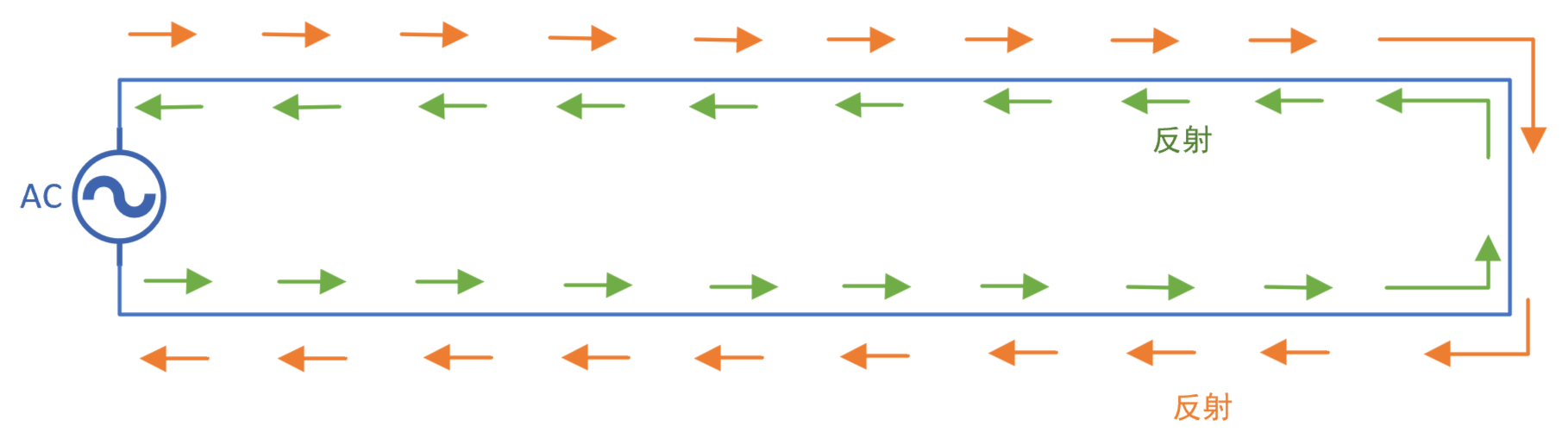

假设双线收端断路,那么脉冲能量也无法在传输线收端被吸收,并且在收端完全被反弹,此时脉冲电流变为零,反射的电压信号与入射的电压信号同向,这样的反射现象是非反向反射(reflection without inversion)。
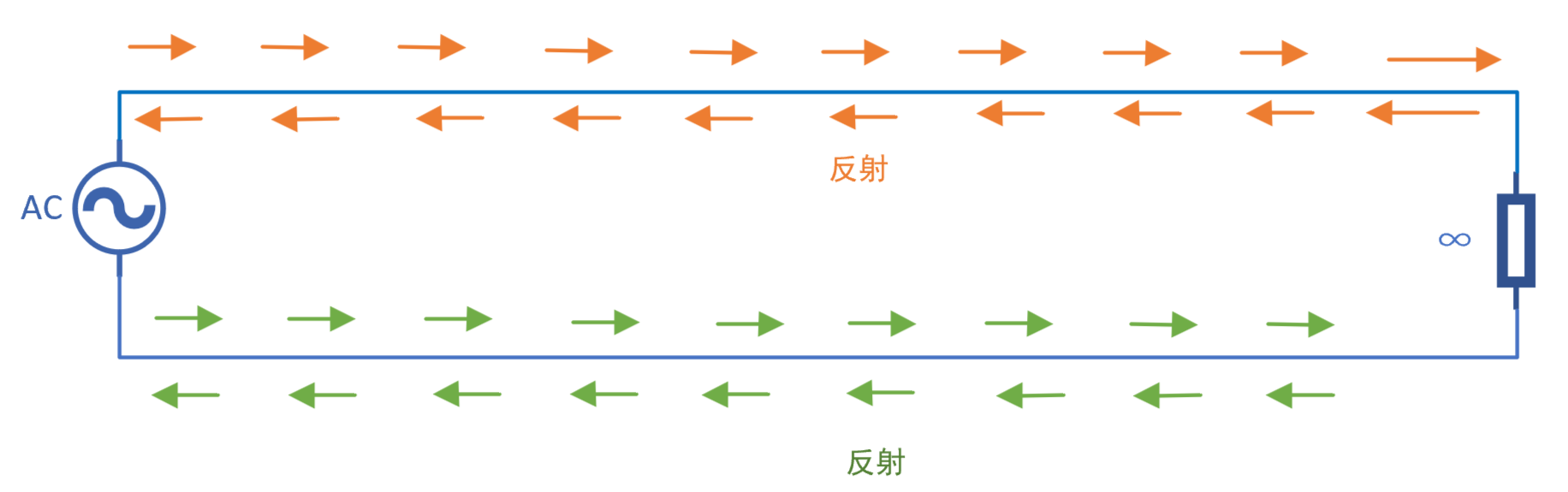

当传输线的特征阻抗与末端阻抗相同时,末端阻抗可以完全吸收发射能量,此时不会出现反射波,这样的情况称为阻抗匹配(matched impedance)。
当传输线的特征阻抗与收端阻抗未能匹配时,信号会部分反射回发端。如果反射信号能够到达发端,那么该信号继续反射多次。
反射系数
设反射电流、电压分别为\(\mathbf{I_r}\)和\(\mathbf{V_r}\),入射(输入)电流、电压分别为\(\mathbf{I_i}\)、\(\mathbf{V_i}\),它们内部通过正负性表达传输方向,整个传输线上的电流电压为:
\[\mathbf{V_L}=\mathbf{V_i}+\mathbf{V_r}\] \[\mathbf{I_L}=\mathbf{I_i}+\mathbf{I_r}\] 那么位于传输线末端的负载的阻抗为:
\[Z_L=\frac{\mathbf{V_i}+\mathbf{V_r}}{\mathbf{I_i}+\mathbf{I_r}}=\frac{1+Γ}{1-Γ}\] 传输线的特征阻抗为:
\[Z_0=\frac{\mathbf{V_r}}{\mathbf{I_r}}=\frac{\mathbf{V_i}}{\mathbf{I_i}}\] 定义反射系数(reflection coeffientient)为反射电压/电流与入射电压/电流之比:
\[Γ=\frac{\mathbf{V_r}}{\mathbf{V_i}}=\frac{\mathbf{I_r}}{\mathbf{I_i}}\] 有:
\[Γ=\frac{Z_L-Z_0}{Z_L+Z_0}\] 可以发现,如果负载大于传输线特征阻抗,\(Γ>0\),那么此时的反射是非反向反射;如果负载小于传输线特征阻抗,\(Γ<0\),那么此时的反射是反向反射。\(Γ=0\)时,阻抗匹配。
驻波
两列沿相反方向传播的振幅相同、频率相同的波叠加时形成的波叫驻波,驻波的形成会让能量无法向前传播因此更多地在传输线上被损耗。幅度相同的反射波与入射波会形成驻波。当反射波与入射波幅度不相同时,则会形成介于驻波和行波之间的行驻波(partial standing wave)。
根据驻波的特点,可以发现驻波中每隔半个波长(\(\frac{λ}{2}\))就会出现幅度最小的断面,称为波节;每隔半个波长(\(\frac{λ}{2}\))也会出现升降幅度最大的断面,称为波腹。相邻波节和波腹之间的距离为\(\frac{λ}{4}\). 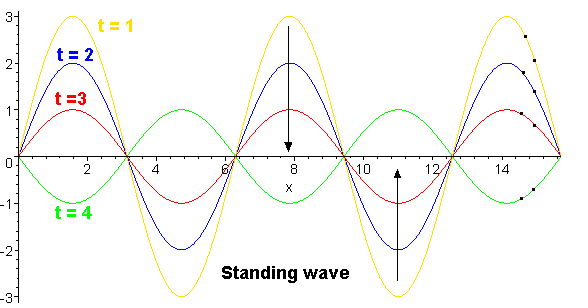
定义形成的行驻波中最大的电压幅度和最小的电压幅度之比(波腹和波节绝对值之比)为电压驻波比(voltage standing wave ratio, VSWR).
\[S=\frac{|\mathbf{V_i}|+|\mathbf{V_r}|}{|\mathbf{V_i}|-|\mathbf{V_r}|}=\frac{1+|Γ|}{1-|Γ|}\] 反推可以得到:
\[|Γ|=\frac{S-1}{S+1}\]
工程应用
在工程应用中,可以通过朝管线发射某个特定频率的波,测量接收到反射波时间来预估管线发生开路的位置。
实际上,完全避免反射波的生成是不可能的。但是如果线路上的损耗足够大,反射波将不会到达发端。工程上,常常使用衰减器在发端附近人为地增加衰减,使得反射波无法影响到发射信号。这样的方法称为填充(padding)。但是这种方法也会削减发射信号的能量。
另一种方法是使用高频工作的无源器件(比如缓冲器)来对反射波进行选择性衰减而不衰减发射信号。这种方法称为隔离(isolation)。
热噪声
在传输过程中的噪声主要是热噪声(Johanson-Nyquist Noise/Thermal Noise),它是由于热效应使导体内部电子热运动而造成的噪声,是一种不可消除的高斯白噪声。在任何阻抗匹配的传输系统中,热噪声功率可以表示为:
\[N=kTB\left[\frac{\frac{hf}{kT}}{e^{-(\frac{hf}{kT})}}\right]\]
其中\(k\)是玻尔兹曼常数,\(T\)是环境的开尔文温度,\(B\)是接收信号带宽,\(h\)是普朗克常数,\(f\)是接收信号的中间频率。
在室温下,如果信号频率小于\(10^{12}Hz\),则\(\left[\frac{\frac{hf}{kT}}{e^{-(\frac{hf}{kT})}}\right]=1\),有:
\[N=kTB\]
金属传输线类型
同轴线
同轴线(Coaixal Line, COAX)是现在最常用的传输线之一。工程中,同轴线常用作馈线或者桌面端传输的线材。
同轴线可以在较短距离内传输高频信号。理论上,同轴线支持的带宽上限为∞。在低频段,相较于双绞线或者平行双线,同轴线的色散效应更为明显。在高频段,由于趋肤效应同轴电缆的电流会在外导体的内表面流动,此时电磁场传播收到外导体内表面性质的影响,其向外辐射的能量减弱,并且串扰更小。
同轴线内径和外径的相对半径决定了同轴线的特征阻抗,标准同轴线的特征阻抗有两种:75Ω或者50Ω.
在实用中,外导体一般用作屏蔽,采取单端接地的措施避免接地点电位不同,引起接地电流干扰内导体中的信号电流。

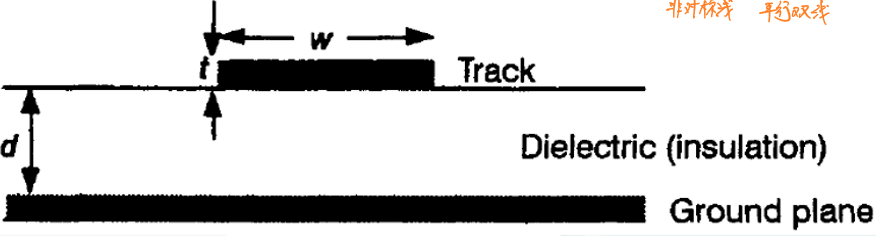
微带线
微带线(microstrip line)是另一种支持高频信号传输的金属传输线,其支持的传输距离比同轴线更短,一般用于电路中两个模块之间的高频信号传输。通常微带线被预制在电路板上。微带线的结构如下图所示: