15. 离散系统的状态空间的表示和补偿器设计

离散系统的状态空间的表示和补偿器设计

离散系统的状态空间表示

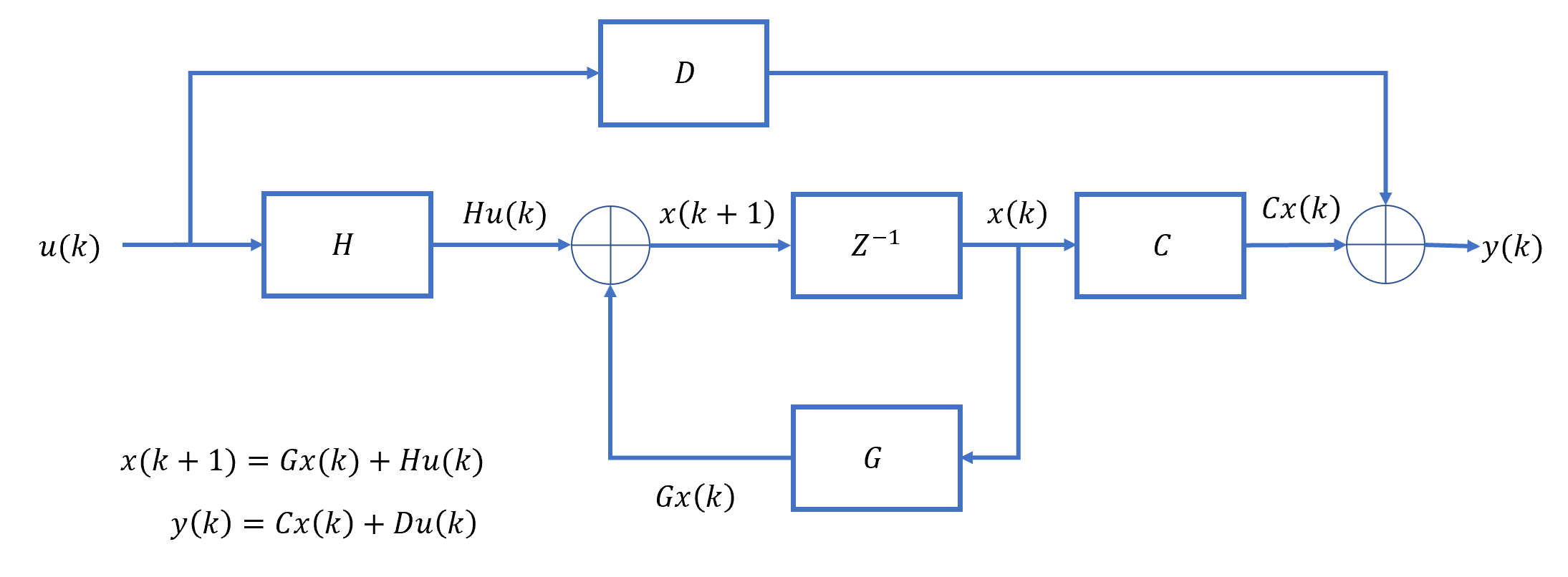
像连续系统的状态空间，对于线性时不变的离散系统，也可以取一组系统的状态变量，使得在已知\(k\)时刻的系统状态和系统输入的情况下，可以知道\(k+1\)时刻的系统状态有：
\[x(k+1)=G\vec{x}(k)+Hu(k)\] 上述方程称为离散系统的状态方程。\(G\)称为状态矩阵，\(H\)称为输入矩阵。
此时系统的输出\(y\)可以表示为:
\[y(k)=C\vec{x}(k)+Du(k)\] 上述方程称为离散系统的输出方程。\(C\)称为输出矩阵，\(D\)称为直接传输矩阵(direct transmission matrix)。
同理可以得到系统的特征方程为：
\[|zI-G|=0\]

状态空间的表达形式

对于描述系统的差分方程：
\[y(k)+a_1y(k-1)+a_2y(k-2)+...+a_ny(k-n)=b_0u(k)+b_1u(k)+...+b_nu(k-n)\]

能控标准型

如果系统的传递函数以如下形式表达：
\[\frac{Y(z)}{U(z)}=\frac{b_0+b_1z^{-1}+...+b_nz^{-n}}{1+a_1z^{-1}+...+a_nz^{-n}}\] 那么系统的状态空间表示可以写作如下两种：
- 其一 \[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0 & ... & 0\\ 0 & 0 & 1 & ... & 0\\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & ... & 1\\ -a_n & -a_{n-1} &-a_{n-2} & \dots & -a_1 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} 0 \\ 0 \\ ⋮ \\ 0 \\ 1 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} b_n-a_nb_0 & b_{n-1}-a_{n-1}b_0 & ... & b_1-a_1b_0 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

• 其二 \[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} -a_1 & -a_2 &-a_3 & ... & -a_{n-1}& -a_n\\ 1 & 0 & 0 & ... & 0 & 0\\ 0 & 1 & 0 & ... & 0 & 0\\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮\\ 0 & 0 & 0 & ...& 1 & 0 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} 1 \\ 0 \\ ⋮ \\ 0 \\ 0 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} b_1-a_1b_0 & b_2-a_2b_0 & ... & b_n-a_nb_0 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

上述两种形式都称为能控标准型，注意其一和其二中对于状态变量的选取的顺序是不同的。

能观标准型

如果系统的传递函数以如下形式表达：
\[\frac{Y(z)}{U(z)}=\frac{b_0+b_1z^{-1}+...+b_nz^{-n}}{1+a_1z^{-1}+...+a_nz^{-n}}\] 那么系统的状态空间表示可以写作如下两种：
- 其一
\[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} 0 & 0 & ... & 0 & 0 & -a_n\\ 1 & 0 & ... & 0 & 0 & -a_{n-1}\\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮\\ 0 & 0 & ...& 1 & 0 & -a_2\\ 0 & 0 & ...& 0 & 1 & -a_1 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} b_n-a_nb_0 \\ b_{n-1}-a_{n-1}b_0 \\ ⋮ \\ b_2-a_2b_0 \\ b_1-a_1b_0 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} 0 & 0 & ... & 0 & 1 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

• 其二
  \[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} -a_1 & 1 & 0 & ... & 0 & 0 \\ -a_2 & 0 & 1 & ... & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮\\ -a_{n-1} &0 & 0 & ...& 0 & 1\\ -a_n&0 & 0 & ...& 0 & 0 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} b_1-a_1b_0 \\ b_2-a_2b_0 \\ ⋮ \\ b_{n-1}-a_{n-1}b_0 \\ b_n-a_nb_0 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} 1 & 0 & ... & 0 & 0 \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

上述两种形式都称为能观标准型，注意其一和其二中对于状态变量的选取的顺序是不同的。

对角型和约旦标准型

如果系统的传递函数以如下形式表达：
\[\frac{Y(z)}{U(z)}=∑\frac{c_i}{z-p_i}\] 那么传递函数的极点可以作为状态矩阵的特征值，有：
\[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} p_1 & 0 & ... & 0\\ 0 & p_2 & ... & 0 \\ ⋮ & ⋮ & & ⋮ \\ 0 & 0 & ... & p_n \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} 1 \\ 1 \\ ⋮ \\1 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} c_1 & c_2 & ... & c_n \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

如果存在重极点，那么此时的表达为约旦标准型，如果\(p_1\)为重极点，有：
\[\begin{bmatrix} x_1(k+1)\\x_2(k+1)\\...\\x_{n-1}(k+1)\\x_n(k+1) \end{bmatrix}=\begin{bmatrix} p_1 & 0 & ... & 0\\ 0 & p_1 & ... & 0 \\ ⋮ & ⋮ & & ⋮ \\ 0 & 0 & ... & p_n \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+\begin{bmatrix} 0 \\ 0 \\ ⋮ \\1 \end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix} c_1 & c_2 & ... & c_n \end{bmatrix}\begin{bmatrix} x_1(k)\\x_2(k)\\...\\x_{n-1}(k)\\x_n(k) \end{bmatrix}+b_0u(k)\]

状态空间表示与系统框图

简单来说，根据系统框图推出系统状态空间表示的方法是：
将系统每一个延迟单元的输出设为一个状态变量\(x_i(k)\)，则延迟单元前的状态为\(x_i(k+1)\)。系统的每一个延迟单元可以写出一个系统的状态方程。
根据系统的输出和各状态之间的关系，可以系统的状态方程。

系统框图与能控标准型

系统框图的级联形式对应系统的能控标准型，简单来说：
对于\(\frac{Y(z)}{U(z)}=\frac{b_0+b_1z^{-1}+...+b_nz^{-n}}{1+a_1z^{-1}+...+a_nz^{-n}}\)，有：
\[\frac{Y(z)}{U(z)}=\frac{Y(z)}{H(z)}\frac{H(z)}{U(z)}\] 那么：\(\frac{H(z)}{U(z)}=\frac{1}{1+a_1z^{-1}+...+a_nz^{-n}}\)，\(\frac{Y(z)}{H(z)}=b_0+b_1z^{-1}+...+b_nz^{-n}\)。对\(\frac{H(z)}{U(z)}\)，有：
\[H(z)(1+a_1z^{-1}+...+a_nz^{-n})=U(z)\] \[H(z)=U(z)-(a_1z^{-1}+...+a_nz^{-n})H(z)\] 根据上述式子，\(\frac{H(z)}{U(z)}\)的信号框图可以作出，例如\(H(z)=U(z)-(a_1z^{-1}+a_2z^{-2})H(z)\) 的框图如下图所示：

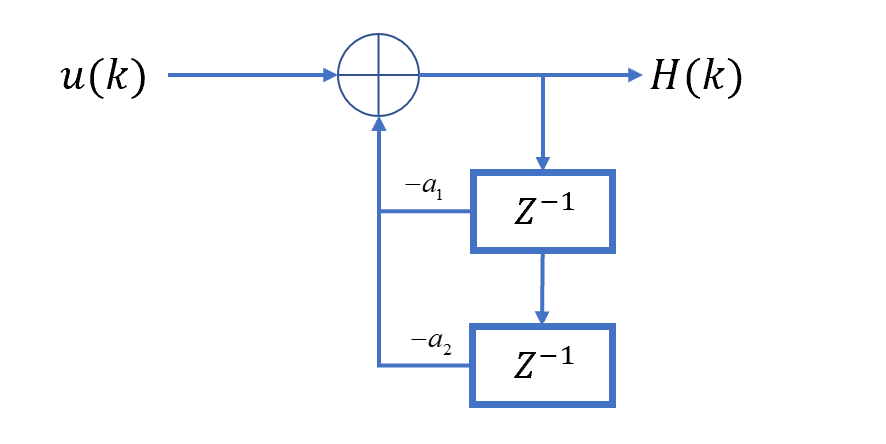
对\(\frac{Y(z)}{H(z)}\)，有：
\[Y(z)=(b_0+b_1z^{-1}+...+b_nz^{-n})H(z)\] 根据上述式子，\(\frac{Y(z)}{H(z)}\)的信号框图可以作出，例如\(Y(z)=(b_0+b_1z^{-1}+b_2z^{-2})H(z)\)的系统框图为：

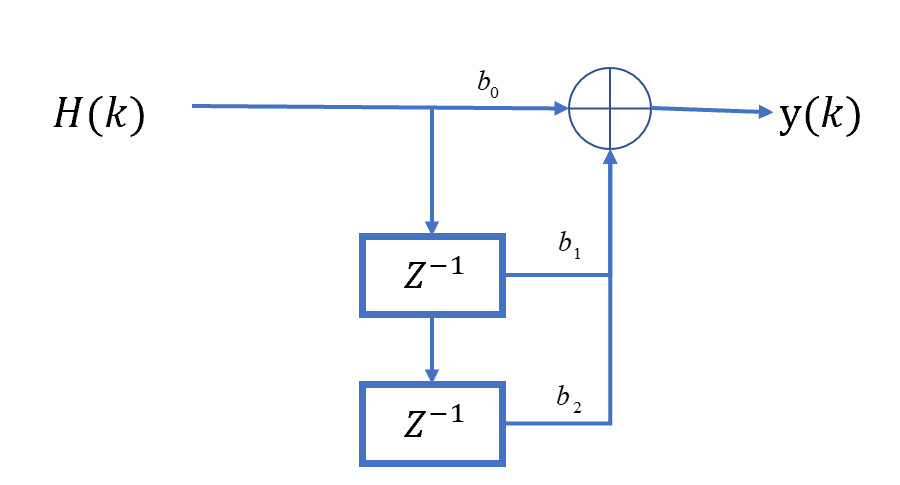
将两部分合并，可以得到：

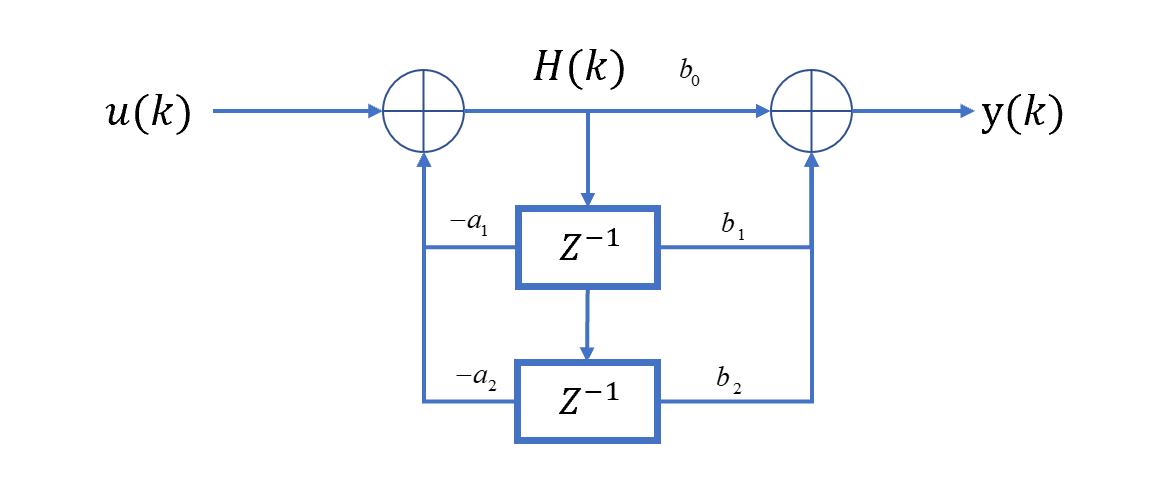
对每一个延迟器前后设置一个状态变量\(x_i(k+1)\)：

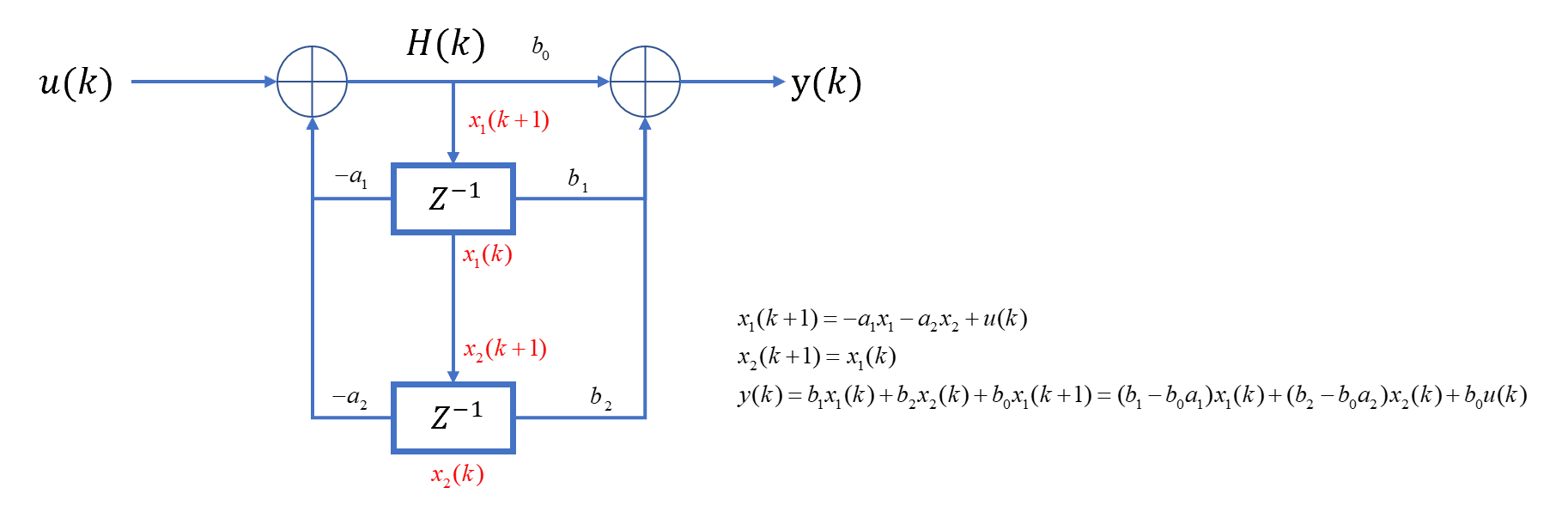
\(x_1(k+1)\)和\(x_2(k+1)\)的位置是可以调换的，因此能控标准型有两种写法。

对\(x_1(k+1)\)，可以得到：
\[x_1(k+1)=-a_1x_1(k)-a_2x_2(k)+u(k)\] 对\(x_2(k+1)\)，可以得到： \[x_2(k+1)=x_1(k)\] 对输出\(y(k)\)可以得到： \[y(k)=(b_1-b_0a_1)x_1(k)+(b_2-b_0a_2)x_2(k)+b_0u(k)\] 根据上述三个式子可以写出系统的能控标准型：
\[\begin{bmatrix}x_1(k+1)\\x_2(k+1)\end{bmatrix}=\begin{bmatrix}-a_1&-a_2\\1&0\end{bmatrix}\begin{bmatrix}x_1(k)\\x_2(k)\end{bmatrix}+\begin{bmatrix}1\\0\end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix}b_1-b_0a_1&b_2-b_0a_2\end{bmatrix}\begin{bmatrix}x_1(k)\\x_2(k)\end{bmatrix}+b_0u(k)\]

能观标准性与系统框图

对于\(\frac{Y(z)}{U(z)}=\frac{b_0+b_1z^{-1}+...+b_nz^{-n}}{1+a_1z^{-1}+...+a_nz^{-n}}\)，有：
\[Y(z)(1+a_1z^{-1}+...+a_nz^{-n})=U(z)(b_0+b_1z^{-1}+...+b_nz^{-n})\] \[Y(z)=U(z)(b_0+b_1z^{-1}+...+b_nz^{-n})-Y(z)(a_1z^{-1}+...+a_nz^{-n})\] 接下来，不断地提取\(z^{-1}\)项。比如对于\(Y(z)=U(z)(b_0+b_1z^{-1}+b_2z^{-2})-Y(z)(a_1z^{-1}+a_2z^{-2})\)，有：
\[\begin{aligned} Y(z)=&U(z)b_0+z^{-1}[b_1U(z)+b_2z^{-1}U(z)-Y(z)a_1-Y(z)a_2z^{-1}]\\ =&U(z)b_0+z^{-1}[b_1U(z)-Y(z)a_1+z^{-1}(b_2U(z)-Y(z)a_2)] \end{aligned}\] 接下来，从最内部的\(b_2U(z)-Y(z)a_2\)开始构建系统，直到用框图搭建完整个系统为止，整个系统的框图如下方所示：

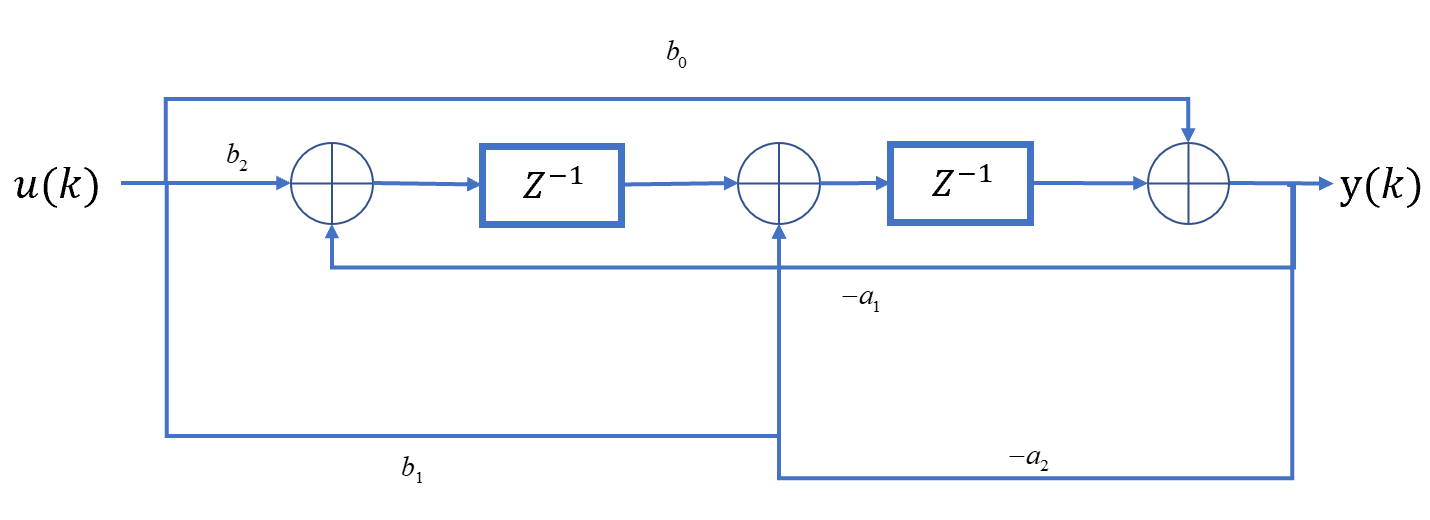
对每一个延迟器前后设置一个状态变量\(x_i(k+1)\)：

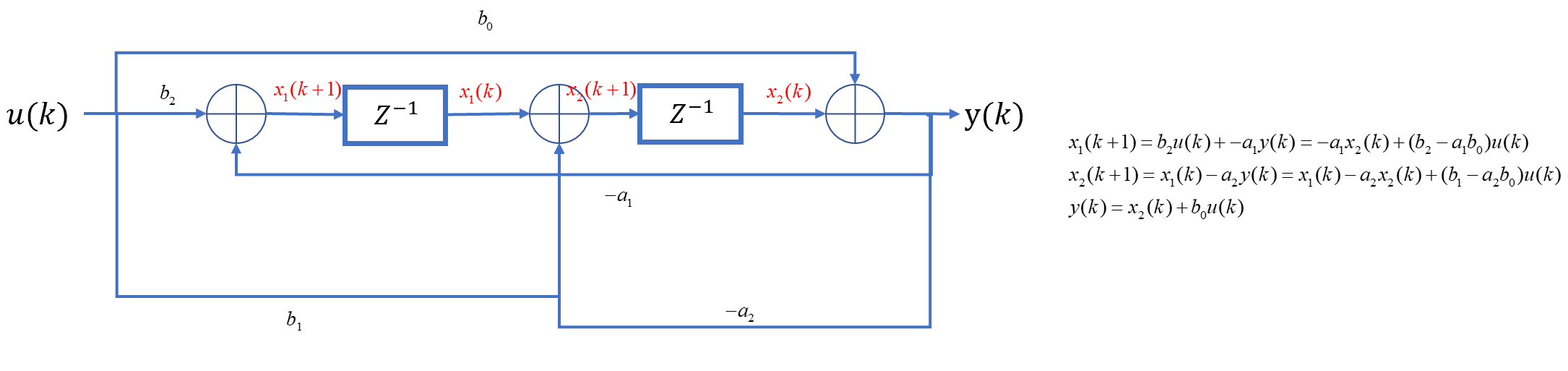
\(x_1(k+1)\)和\(x_2(k+1)\)的位置是可以调换的，因此能观标准型有两种写法。

有：
\[x_1(k+1)=-a_1x_2(k)+(b_2-a_1b_0)u(k)\] \[x_2(k+1)=x_1(k)-a_2x_2(k)(b_1-a_2b_0)u(k)\] \[y(k)=x_2(k)+b_0u(k)\] 综合以上三式，有：
\[\begin{bmatrix}x_1(k+1)\\x_2(k+1)\end{bmatrix}=\begin{bmatrix}0&-a_1\\1&-a_2\end{bmatrix}\begin{bmatrix}x_1(k)\\x_2(k)\end{bmatrix}+\begin{bmatrix}b_2-a_1b_0\\b_1-a_2b_0\end{bmatrix}u(k)\] \[y(k)=\begin{bmatrix}0&1\end{bmatrix}\begin{bmatrix}x_1(k)\\x_2(k)\end{bmatrix}+b_0u(k)\]

连续系统状态空间表示的离散化

对于连续系统：\(\begin{cases}\vec{\dot{x}}=A\vec{x}+Bu \\ y(t)=C\vec{x}+Du\end{cases}\)，根据 映射律\(z=e^{sT}\)，有:
\[G=e^{AT}=\mathcal{L}^{-1}((sI-A)^{-1})\] \[H=(\int_0^Te^{Aλ}dλ)B=(G-I)A^{-1}B\] 即可得到离散化后的系统状态空间表示：
\[x(k+1)=Gx(k)+Hu(k)\] \[y(k)=Cx(k)+Du(k)\]

需要注意的是，\(G\)和\(H\)会随着采样周期\(T\)的变化而变化。

离散系统的能控性和能观性

能控性判定

根据系统能控性的定义，如果系统的控制信号与系统的状态变量独立，则系统是能控的。换言之，对于任意\(n\)，倘若\(G^{n-1}\)都与\(H\)独立，则系统是能控的。
定义离散系统的能控性矩阵：
\[[H|GH|…|G^{n-1}H]\] 即能控性矩阵满秩，即\(|[H|GH|…|G^{n-1}H]|≠0\)，则系统是能控的。

能观性判定

根据系统能观性的定义，如果系统任何状态转换都会影响每一个输出变量，那么系统是能观的。
定义离散系统的能观性矩阵：
\[\begin{bmatrix} C\\ - \\ CG \\ - \\ ... \\ - \\ CG^{n-1} \end{bmatrix}\] 如果离散系统的能观性矩阵满秩，即\(|\begin{bmatrix} C\\ - \\ CG \\ - \\ ... \\ - \\ CG^{n-1} \end{bmatrix}|≠0\)，则系统是能观的。

反馈控制器

反馈控制系统的特征方程

对于系统\(\begin{cases} \vec{x}(k+1)=A\vec{x}(k)+Bu(k)\\ y(k)=C\vec{x}(k) \end{cases}\):
添加一个负反馈控制器\(K\):

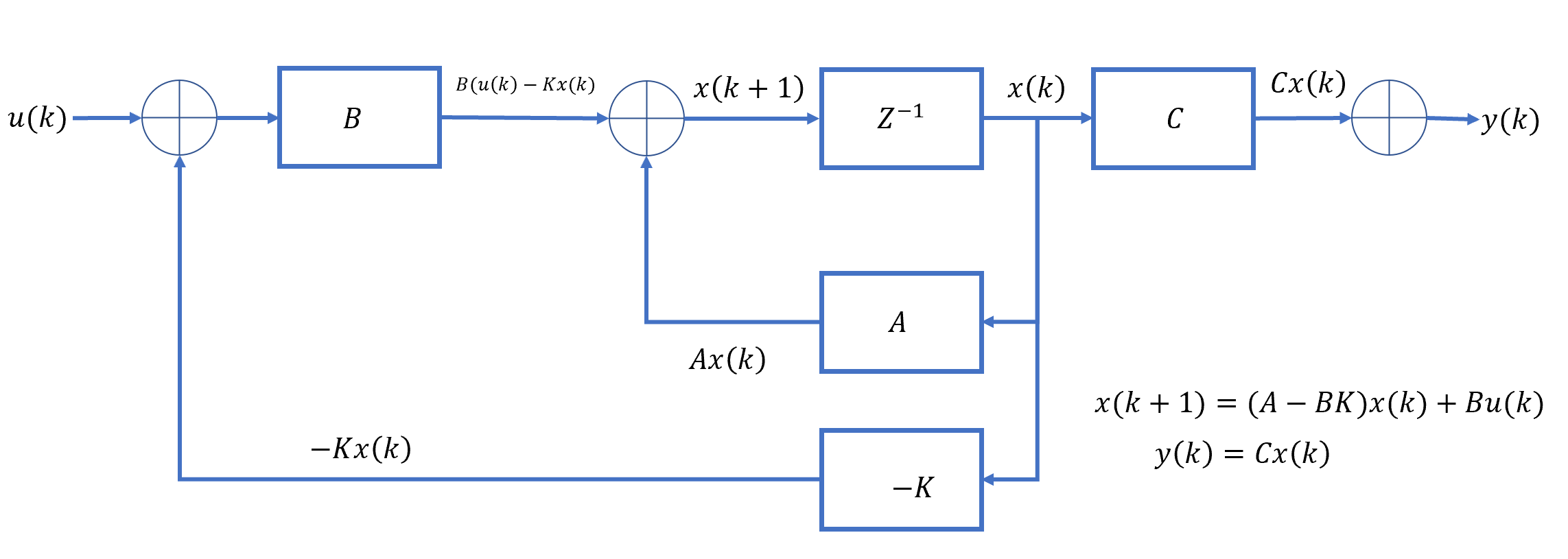
根据上图，有系统的状态方程：
\[x(k+1)=Ax(k)+Bu(k)\]

带入\(u(k)=-kx(k)+v(k)\)，有：
\[x(k+1)=(A-BK)x(k)+Bv(k)\] 其中， \[|zI-(A-BK)|=0\] 是系统的特征方程。

反馈控制器设计步骤

• 检验系统原型的能控性矩阵。
  
• 根据系统的设计要求，找到阻尼比\(ζ\)和固有频率\(ω_n\)，并构造出系统的特征多项式。
  
• 设计系统的反馈控制器，并且根据\(|zI-(A-BK)|\)找到系统含有\(k_i\)的特征多项式。
  
• 通过两种方法得出的特征多项式进行系数匹配，得到\(K\)。

观测器设计

对于系统\(\begin{cases} \vec{x}(k+1)=A\vec{x}(k)+Bu(k)\\ y(k)=C\vec{x}(k) \end{cases}\): 增加一个观测器：

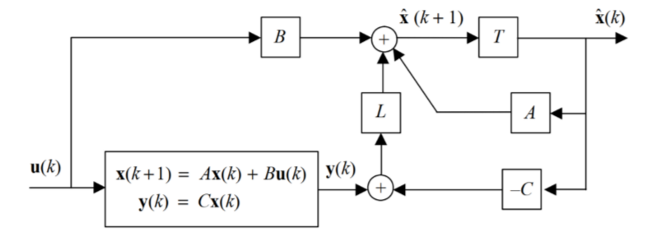
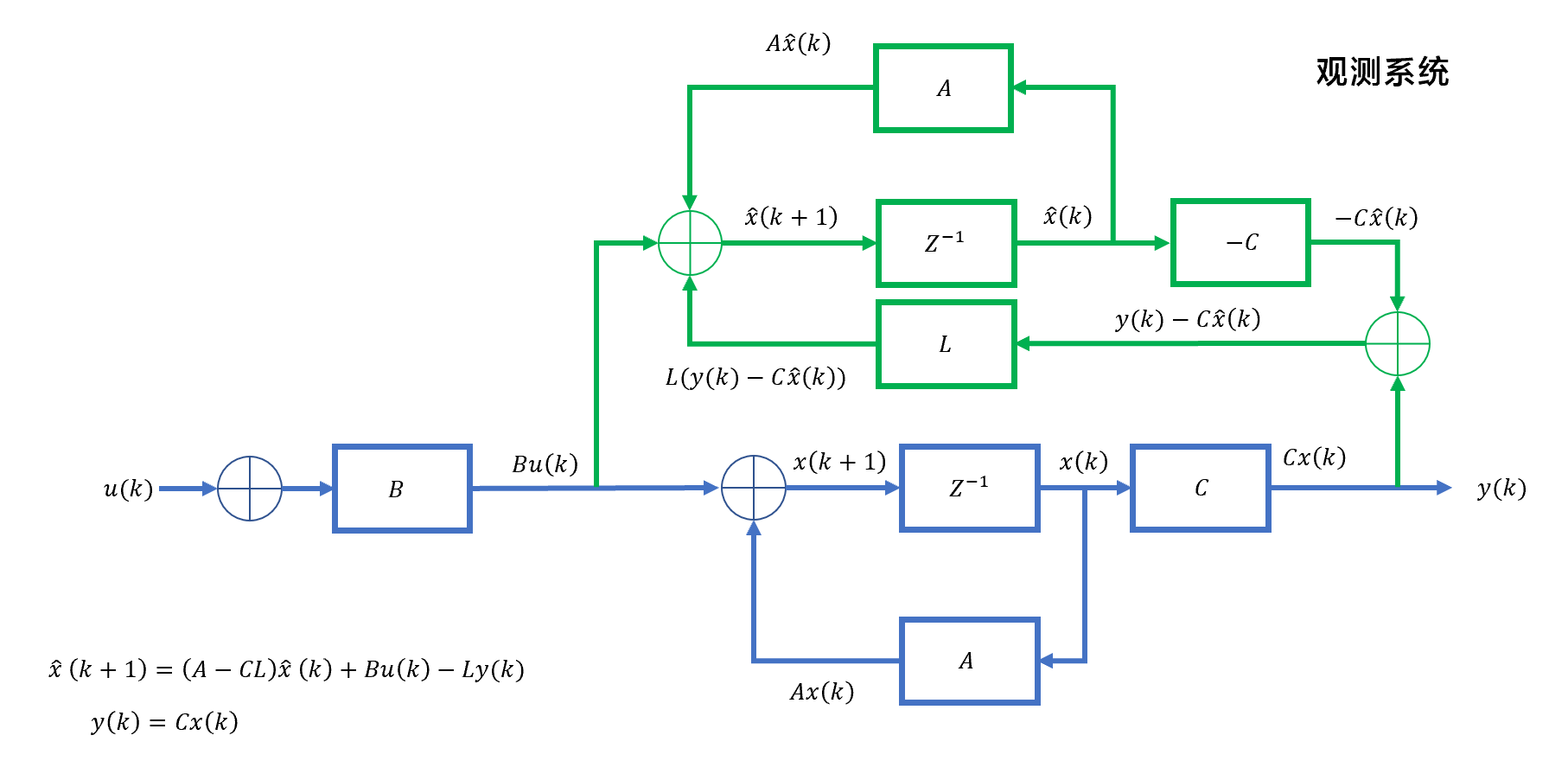
观测器的功能

系统在下一个时刻的状态估计量为\(\vec{\hat{x}}(k+1)\)，它可以通过观测器得到：
\[\vec{\hat{x}}(k+1)=A\vec{\hat{x}}+Bu(k)+L[y(k)-C\vec{\hat{x}}(k)]\] 设系统的观测状态误差为观测器估计的系统下一时刻状态的观测值和系统下一时刻状态的实际值之差：
\[\vec{x_e}(k+1)=\vec{x}(k+1)-\vec{\hat{x}}(k+1)\] 结合\(\vec{x}(k+1)=A\vec{x}(k)+Bu(k)\)，有：
\[\vec{x_e}(k+1)=A\vec{x_e}(k)-L[y(k)-C\vec{\hat{x}}(k)]\] 根据\(y(k)=C\vec{x}(k)\)，有\(\hat{y}(k)=C\vec{\hat{x}}(k)\)，那么：
\[\vec{x_e}(k+1)=A\vec{x_e}(k)-L[y(k)-\hat{y}(k)]\] 可以发现，通过调整观测器系数\(L\)，可以使得下一次系统的状态误差随着本次系统的输出误差的减少而减少。
同时，带入\(y(k)=C\vec{x}(k)\)，可以发现系统状态误差的转移： \[\vec{x_e}(k+1)=A\vec{x_e}(k)-LC[\vec{x}(k)-\vec{\hat{x}}(k)]\] 即：
\[\vec{x_e}(k+1)=(A-LC)\vec{x_e}(k)\] 那么系统状态误差的状态转移矩阵为：
\[A-LC\] 系统的特征方程为：
\[|zI-(A-LC)|=0\]

观测器设计步骤

• 检验系统原型的能观性矩阵。
  
• 根据系统的设计要求，找到阻尼比\(ζ\)和固有频率\(ω_n\)，并构造出系统的特征多项式。
  
• 设计系统的反馈控制器，并且根据\(|zI-(A-LC)|\)找到系统含有\(l_i\)的特征多项式。
  
• 通过两种方法得出的特征多项式进行系数匹配，得到\(K\)。