2.无线信道

无线信道

无线电波传播环境

电磁波传播现象

在自由空间中，无线电波的传播是点对点的视距传播。然而实际传播中，无线电波在传播过程中会遇到各种各样的障碍物，由此发生各种类型的传播现象。这些传播现象会导致无线电波的原有性质发生改变。

• 反射(reflection)
  电磁波遇到大型障碍物（指障碍物尺寸远远大于电磁波波长）时发生能量损耗和传播方向的变化，能量损耗由吸收或电磁波进入障碍物介质引起。
  
• 散射(scattering)
  电磁波在传播过程中遇到小型障碍物和粗糙表面时，反射能量散布于所有方向。
  
• 绕射(diffraction)
  波遇到尖锐障碍物（尤其为刃形障碍物）时偏离原来直线传播的物理现象。

无线电波传播效应

因为电磁波在实际环境下的传播现象，会使得接收的波形幅度发生随机的起伏(flactuation)变化，同时波形展宽，在时域上频谱延展。具体而言，造成波形起伏变化的原因有四：

路径损耗

无线电信号通过大尺度距离的信道传输时，随传输路径的增加，电波能量扩散，导致接收信号平均功率衰减，其衰减量与传输距离有关，距离越大，衰减量越多。路径损耗是发送功率与接收的平均功率的差值。
大多数的路损模型中认为自由空间损耗是理论上信号遭受的最小路损，自由空间损耗可以描述为：
\[L_{fs}|_{dB}=32.44+20lgd_{km}+20lgf_{Mhz}\]

阴影效应

阴影效应是指在无线通信系统中，移动台在运动的情况下，由于大型建筑物和其他物体对电波的传输路径的削弱甚至阻挡而在传播接收区域上形成半盲区，从而形成电磁场阴影，这种随移动台位置的不断变化而引起的接收点场强中值的起伏变化叫做阴影效应。
阴影效应由反射、散射和绕射三个传播现象共同造成，信号的衰落程度与位置有关。由阴影效应造成的信号衰落变化都是随机的变化，其服从对数正态分布。

多径效应

在接收机和发信机之间，由于反射、散射和绕射导致电磁波的传输路径并不唯一，沿不同路径传输的电磁波到达接收机的时间不一样的现象称为多径效应。
多径效应导致在接收机一侧观察到信号在时域上发生延展，称为时延扩展(time dispersion)，这是导致码间串扰的直接原因。
同时，不同传播时间下，原来电磁波的波形\(Asin(ωt+φ)\)通过时延\(Δt\)后成为\(Asin(ωt+φ+ωΔt)\)，使得波形相位发生改变。不同相位的波形叠加，可能使得原有的幅度被抵消或者加强，产生波形的起伏。

多普勒效应

接收者移动时，其接收到的波会发生频移。如果接收者远离波源移动，则接收到的频率会逐渐降低。如果接收者靠近波源移动，则接收到的频率会逐渐升高。
多普勒效应的频移量表示为：
\[Δf=-\frac{1}{2π}\frac{Δφ}{Δt}=\frac{v}{λ}cosα\] 其中\(α\)是接收者与波源连线与水平面的夹角。

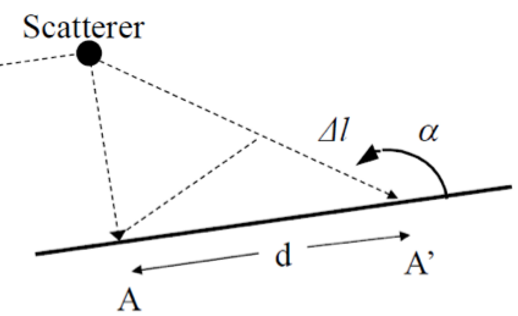
有\(Δf\)的最大值为：
\[Δf_{max}=\frac{v}{λ}=\frac{v}{c}f\] 可以发现多普勒频移和移动台的相对移动速度\(\frac{v}{c}\)有关。

信号衰落

由于这些电磁波传播效应，最终会导致信号在传播过程中能量的衰减，称为衰落。信号衰落可以分为信号幅度相对缓慢变化长期衰落/慢衰落和信号幅度剧烈变化的短期衰弱/快衰落。长期衰落由阴影效应造成，短期衰落由多普勒效应和多径效应造成。长期衰落和短期衰落在传播过程中同时出现，只是对传播信号分析的时间尺度不同。

为了简化理解，本课程中认为由阴影效应造成的大尺度衰落是长期衰落或者称为慢衰落;由多普勒效应和多径效应造成的小尺度衰落又可以称为短期衰落或者是快衰落。

详细而具体的分类如下图所示：

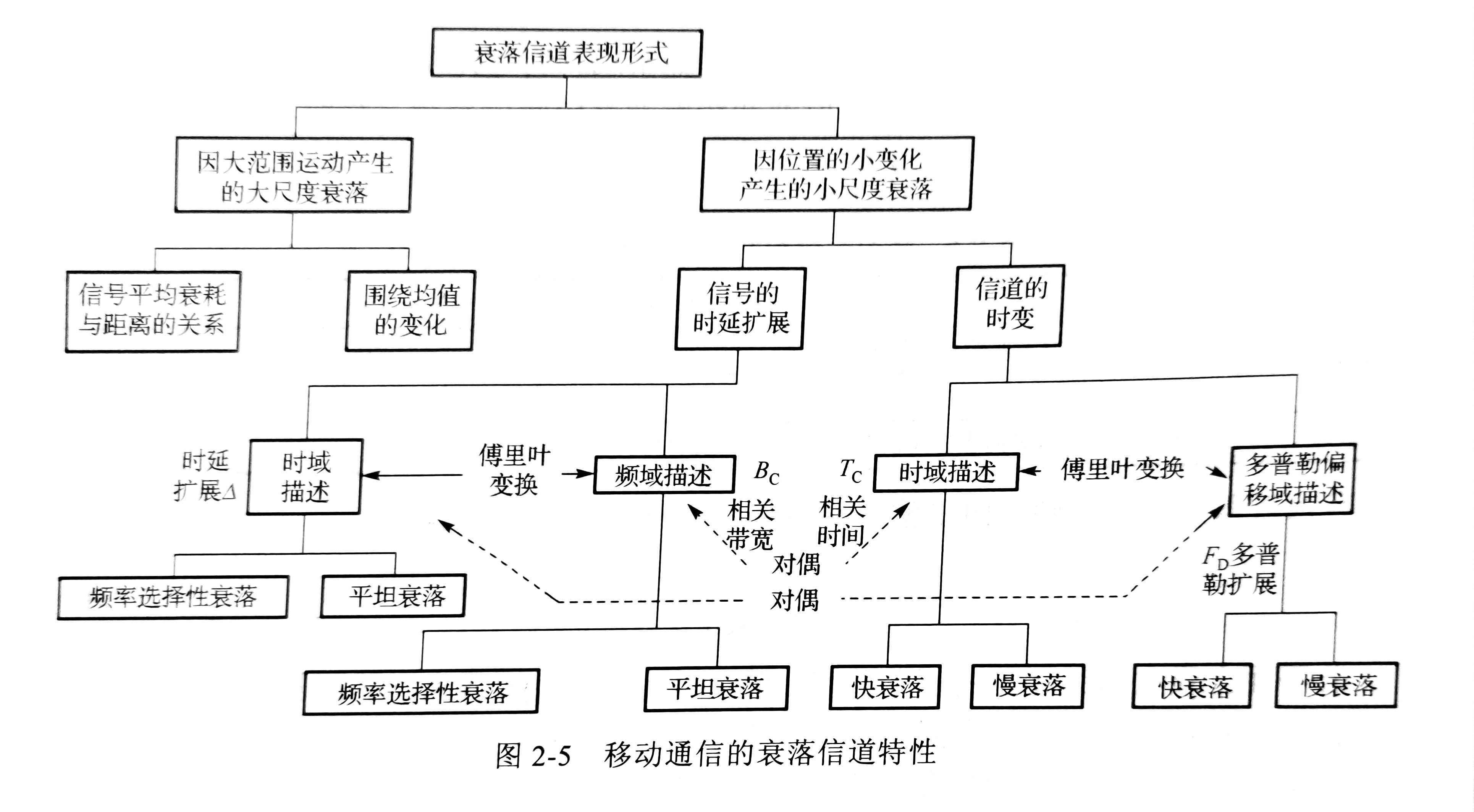
噪声

在传播的过程中由于各种各样的因素，会造成接收方除了接收到有衰落的原调制信号外，还会接收到某些杂信号，这些杂信号称为噪声(noise)。噪声分为来自传输器件的内部噪声和环境中的外部噪声。

外部噪声

移动通信中需要考虑到的外部噪声主要有三类：

• 大气噪声(atmospheric noise)
  大气噪声的主要噪声源是电离层中的带电粒子，这些带电粒子的放电会产生噪声。大气噪声的功率随着时间、季节、天气的变化而变化。
  
• 宇宙噪声(cosmic noise)
  宇宙噪声的主要噪声源是大气层外某些星体的自然辐射和宇宙射线，在移动通信中主要考虑太阳的辐射。
  
• 人为噪声(man-made noise)
  由于人类活动和人造电子设备产生的噪声。产生人为噪声的主要噪声源是汽车的点火器、电动马达、电视接收天线等。移动通信中主要考虑汽车的点火噪声。

内部噪声

最典型的内部噪声是热噪声(thermal noise)，它是一种加性高斯白噪声(AWGN)，由电子和电路器件内部粒子的热运动产生。热噪声的功率可以表示为：
\[N=kTBF\] 其中，\(k=1.3805×10^{-23}J/K\)为玻尔兹曼常数；\(T\)为环境的开尔文温度；\(B\)为带宽；\(F\)为噪声系数，在理想条件下\(F=1\)。
对数化后为：
\[N|_{dB}=[kTBF]=-228.6+10lgT|_{K}+10lgB|_{Hz}+F|_{dB}\]

路径损耗模型

无线传输链路模型

基本的无线传输链路模型由接收天线和发送天线的功率\(P_t\)和\(P_r\)以及它们的增益\(G_t\)和\(G_r\)、以及传播过程中的损耗\(L\)组成：
\[P_r|_{dB}=P_t|_{dB}+G_t|_{dB}+G_r|_{dB}-L|_{dB}\]

移动通信中最关心的问题是无线电波在发送机和接收机之间传播过程当中的损耗。定义路径损耗(path loss)为发送机发送的信号功率和接收机接收信号的平均功率之比。

知道无线电波在具体环境中的路径损耗可以得到接收信号的功率、从而得到一个大致的信号覆盖范围，从而帮助规划位置和数量天线的设置，还可以帮助确定发送天线功率、增益和尺寸的设置（称为链路预算）。
同时，利用路径损耗模型也可以实现对于移动台的定位。
路径损耗模型则是通过实验和理论分析，将具体环境下的路径损耗通过数学模型表达出来。路径损耗模型的分类如下表所示：

名称	特点	设置对象
麦克斯韦方程	1. 有助于了解电磁波在具体空间中的传播特性 2.对于实际工程过于复杂	传输器件：比如天线和传输线
自由空间损耗模型	1. 非常容易计算 2.对于传播环境的描述过于简单，因此过于理想化
经验模型	1.基于实验测量 2.结果通常是基于有限的频率和一些特定的介质 3.缺乏对无线电波传播机制的物理观点(Physical view)	宏蜂窝
半确定性模型	两者的折中方案
确定性模型/射线追踪模型	1.应用十分有限，主要应用于特殊几何结构的情况 2.对不同情况需要不同的传输路径特性(如ɛ和σ) 3.由于考虑了直射、折射和衍射，因此模型十分复杂 4.考虑了不同地形的电参数	微蜂窝和皮蜂窝

麦克斯韦方程*

麦克斯韦方程由四个表示电磁波传播特性的基本电磁学理论等式组成：
\[▿·\vec{E}=\frac{ρ}{ϵ}\] \[▿·\vec{B}=0\] \[▿×\vec{E}=-\frac{∂B}{∂t}\] \[▿×\vec{B}=μ_0\vec{J}+μ_0ϵ_0\frac{∂E}{∂t}\]

麦克斯韦方程在分析基本的传输元件（比如不同类型的天线和传输线）有助于了解电磁波在其中具体的传播情况，对于实际工程而言过于复杂。

自由空间损耗模型

在自由空间中，各种电磁波的传播现象由于不存在障碍物而不存在，因而链路模型中的链路损耗转为自由空间传播损耗：
\[L=L_{fs}\] 如果接收天线和发送天线都为偶极子天线/全向天线，那么\(G_t=G_r=1\) \[L_{fs}=10lg\frac{P_t}{P_r}=-20lg\frac{4πd}{λ}\] 有：
\[L_{fs}|_{dB}=32.4+20lgf_{MHz}+20lgd_{km}\]

从链路模型和自由空间损耗公式可以推断，在自由空间下，发送天线只需要非常小的发送功率即可覆盖千米级别的区域。

馈线损耗

除了考虑传播损耗，在构建自由空间模型时有时候还会考虑到天线与发送系统之间的传输线损耗，这样的损耗称为馈线损耗。馈线损耗与采用的传输线材质有关。

细化的链路模型

在移动通信链路中，发送功率和接收功率的差异除了考虑收发天线增益\(G_t\)和\(G_r\)和路径损耗外，通常还要考虑大气散射损耗\(L_g\)、收发天线的馈线损耗\(L_t\)和\(L_r\)，以及噪声\(N\)，因此在基本无线传输链路模型下，增加了如下的环节：
\[P_r|_{dB}=P_t|_{dB}+G_t|_{dB}+G_r|_{dB}-L_t|{dB}-L_r{dB}-L_{fs}|_{dB}-L_{g}|_{dB}\] 其中：\(P_t|_{dB}+G_t|_{dB}-L_t|{dB}\)为发送机的有效辐射功率。如果采用全向天线，那么天线的增益为\(G|_{dB}=1\)。
载噪比CNR表示为：
\[CNR|_{dB}=P_r|_{dB}-N|_{dB}\]

双射线模型

双射线模型(two ray model)是一种射线追踪模型，在自由空间模型的基础上还考虑了平地反射。双射线模型由一条视距传播链路和一条经过地面反射的链路组成，并且考虑了接收和发送天线的高度\(h_T\)和\(h_R\)：

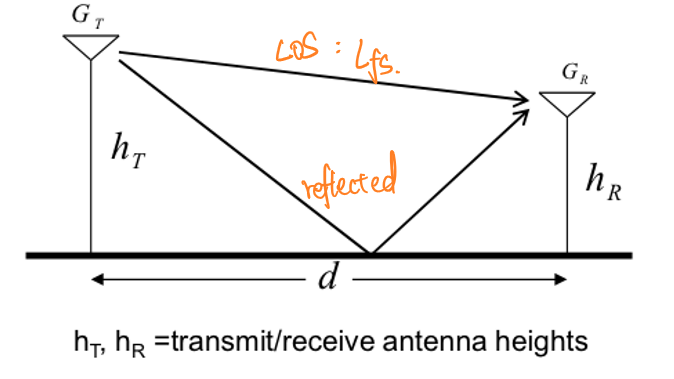
同样根据链路模型可以推导出：
\[L=\frac{1}{4sin^2(\frac{2πh_Th_R}{λd}\left(\frac{λ}{4πd})^2\right)}\] 考虑\(λd>>h_Th_R\)，并使用\(sinx≈x\)近似，可以得到：
\[L=\frac{d^4}{(h_Th_R)^2}\] \[L|_{dB}=40lg(d)-20lg(h_Th_R)\]

相比于自由空间模型，可以发现双射线模型中：

• 衰落与电磁波频率无关
• 相比于自由空间模型\(20lgd\)，双射线模型中的损耗受传播距离影响更大。
  
• 考虑到了收发天线高度对传播的影响。

在微蜂窝和皮蜂窝基站设置中，大部分基站都设置在楼层高度以下，基站间隔距离不远（微蜂窝：半径在1km以下；皮蜂窝：半径在200m以下），接收机接收到的功率与天线位置有很强的关系，此时一般采用确定性模型/射线追踪模型。双射线模型对微蜂窝(microcell)设置的基站间的视距传播损耗预测效果较好，接近实际。
同时，还可以根据环境的具体配制增加反射链路的数量，成为多射线模型/射线追踪模型。但是更多的反射链路数量意味着计算量的剧烈增加，依赖于更多的计算资源和更多的传播环境信息（比如障碍物尺寸）、并且考虑更多的传播效应（比如沟道/街道效应，一种由于街区建筑物统一走向导致电磁波传播受到干扰的效应），多射线模型可以更好的描述视距传播。

简化的路径损耗模型

在简化的路径损耗模型中，链路中接收机接收到的功率可以表示为传播距离的函数：
\[P_r(d)=P_r(d_0)\left(\frac{d_0}{d}\right)^n\] 此时的路径传输损耗可以表示为：
\[L|_{dB}=10nlg\left(\frac{d_0}{d}\right)\] 其中，\(d_0\)是一个单位的参考距离，用于统一单位；\(n\)称为路径衰减指数，路径衰减指数的设置依赖于工程经验，在自由空间中，\(n=2\)。在路径损耗模型中通常考虑的传播环境有三个：城区(urban，\(n=4.5\))、市郊/开阔地带(suburban，\(n=4\))、农村(rural,，\(n=3\))。
虽然简化的路径损耗模型通常比较适用于各种场景，但是简化的路径损耗模型不会考虑波导效应。波导效应(waveguid effect)是一种电磁波遇到形如波导一样整齐规则的中空障碍物时，以反射方式行进的效应。沟道效应(street guiding effects)是一种典型的波导效应。

经验路径损耗模型

在宏蜂窝基站的设置中，由于基站间隔距离较远（半径在0.5km-3km，更大的宏蜂窝基站半径在1km-30km），且基站通常设置在建筑物楼顶，传播环境和传播介质更加复杂，此时通过工程测量和数值校正得到的经验模型更加适用。
常用的经验路径损耗模型是奥村-Hata模型(Okumura-Hata model)。该是由奥村等人在日本东京使用不同的频率和不同的天线高度，选择不同的距离进行一系列测试，最后Hata等人进行拟合绘成经验曲线的模型。最初的奥村-Hata模型指适用于150-1500MHz的无线电波频段，其后欧洲EURO-COST组织基于奥村-Hata模型将其适用频率拓展到1500MHz-2GHz生成的COST 231模型。
奥村-Hata模型/COST 231模型中，路径损耗建模为：
\[L=A+Blg(f|_{MHz})-13.82lg(h_b|_{m})+(C-6.55lg(h_b|_{m}))lg(d|_{km})-K\] 其中，\(h_b\)是基站天线的高度；\(K\)为校正因子，默认\(K=0\).
\(A,B,C\)为调整系数，其中\(C\)的取值范围在44-47之间。在奥村-Hata模型(150-1500MHz)中，\(A=96.55,B=26.16\)；在COST 231模型（1500MHz-2GHz）中，\(A=46.3,B=33.9\)；

不管是奥村-Hata模型还是其后的COST 231模型，其基本模型都是基于城市环境和平坦地形，在 基站天线高度\(h_b=200m\)、移动台天线高度\(h_m=3m\) 的条件下构建的。在其他不为基本条件的情况下，需要增加修正系数。

半经验模型

奥村-Hata模型/COST 321模型只适用于城市和开阔地，半经验模型则是在奥村-Hata模型上的进一步延伸，使其能够拓展到各种环境。基于奥村-Hata模型的半经验模型有：

• Walfisch-Ikegami 模型
  适用于密集人口的城市环境，Walfisch-Ikegami 模型考虑了沟道效应和多径散射等传播效应和现象。
  
• Lee 模型
  适用于中等起伏地形。

室内传播模型

室内传播模型考虑了电磁波在室内的传播，基本的室内传播模型由自由空间损耗和墙与楼层间隔材料的吸收。室内传播模型将路径损耗建模为：
\[L=L_{ref}+20lgd+∑_{fl=1}FAF(fl)+∑_{wl=1}WAF(wl)\] 其中\(L_{ref}\)是\(d=1m\)时的自由空间路径损耗;\(FAF(fl)\)是楼层材料\(fl\)的衰减系数;\(WAF(wl)\)是墙体材料\(wl\)的衰减系数。

衰落模型

在发送信号一定的情况下，接收信号的幅值在一定尺度上变化/起伏（fluctuation）的现象称为衰落（fading）。使用路径损耗模型无法预测到这些起伏。
衰落可以按照持续时间分类为：慢衰落和快衰落，或者按照起伏程度分为：大尺度衰落和小尺度衰落。
衰落模型对试图对接收功率建模从而预测信道衰落。

大尺度衰落模型

大尺度衰落是由于阴影效应和路径损耗造成的。通常大尺度的衰落可以用确定性模型进行建模。
在简化的路径损耗中，考虑大尺度衰落带来的影响\(Ψ\)，此时接收到的信号功率表示为:
\[P_r(d)=P_r(d_0)-10nlg(\frac{d}{d_0})+Ψ|_{dB}\] 其中\(Ψ|_{dB}\)的值服从均值为0的高斯分布。

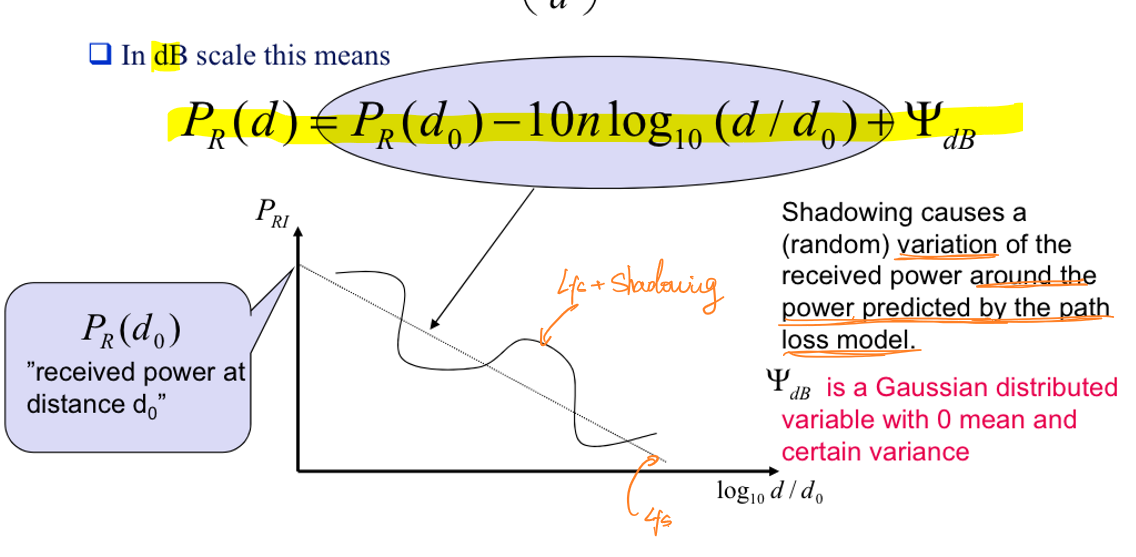
掉话率

掉话率(outage probability)指当接收机接收到的功率小于其灵敏度时，接收机无法处理接收信号的概率。掉话率越低，无线通信链路的稳定性越强。
根据定义，有：
\[p_{out}=p(P_r(d)<P_{min})\] 定义\(\hat{P}_r(d)\)为根据自由空间损耗和链路模型预测到的接收功率，那么有：
\[\begin{aligned} p_{out}&=p(\hat{P}_r(d)+Ψ>P_{min})\\ &=1-p(\hat{P}_r(d)+Ψ<P_{min})\\ &=1-p(Ψ>P_{min}-\hat{P}_r(d)) \end{aligned}\] 由于\(Ψ\)服从正态分布，这个概率可以表示为：
\[p(Ψ>P_{min}-\hat{P}_r(d))=Q(\frac{P_{min}-P_r(d_0)+10nlg(\frac{d}{d_0})}{σ_{Ψ}})\] 其中\(σ_{Ψ}\)是\(Ψ\)的概率分布的标准差；\(Q(x)=\frac{1}{\sqrt{2π}}\int_x^∞e^{-t^2/2}dt\)是标准正态分布的概率分布函数。

小尺度衰落模型

小尺度衰落/多径衰落是无线电波在非常短时间内幅度快速的变化。小尺度衰落是由多径效应和多普勒效应引起。
无线信道是一个线性时变系统，接收到的信号\(r(t)\)在时域上是发送信号\(x(t)\)和时变信道\(h(t)\)的卷积：
\[r(t)=∫h(τ,t)x(t-τ)dτ\] 其中，\(h(τ,t)\)可以描述为信道中各路径的集合，因此\(h(τ,t)\)也可以表示为各路径参数与冲激信号的离散卷积，称为信道冲激响应(channel impulse response)：
\[h(τ,t)=∑_{l=1}^Lα_l(t)δ(τ-τ_l(t))\] \(α_l(t)\)表示为路径\(l\)在\(t\)时刻的增益，\(τ_l(t)\)是链路\(l\)在\(t\)时刻的时延。
路径增益\(α_l(t)\)是一个复数，其实部影响接收信号的幅度，相位影响接收信号的相位。\(α_l(t)\)可以看做是一个服从高斯分布的随机变量：对于视距传播，其方差为0；对于非视距传播，其方差不为0。

时间选择性信道

• 频率拓展
  由于多普勒效应使得无线信号在传播过程中出现中心频点的移动，在接收机侧观察到为同一个符号表征的信号在频域上发生延展，称为频率拓展(frequency dispersion)。由于多普勒效应的影响，信号其中心频率会产生偏移。由于中心频率的频移，信号会对其他载波造成干扰，形成载波间干扰（ICI）。

• 相关时间
  信道可以维持某种状态而不非切换到另一种状态的最大时间称为相关时间/相干时间(\(T_{coh}\)，coherence time)。通常，相干时间。相关时间表示为多普勒最大频移对应的周期：
  \[T_{coh}=\frac{1}{Δf_{max}}=\frac{c}{vf}\] 50%相关时间定义为在间隔小于\(T_{coh}\)秒的时间内测量的信道状态，其相关性大于0.5。

当信道的符号持续时间大于等于相关时间\(T≥T_{coh}\)时，信道称为时间选择性信道/快衰落信道。
当信道的符号持续时间远远小于相关时间\(T<<T_{coh}\)时，信道称为时间平坦信道/慢衰落信道。在这种情况下，信道参数并不是时变的：
\[h(τ,t)=∑_{l=1}^Lα_lδ(τ-τ_l)\]

频率选择性信道

在频域上，信道频率响应是信道冲激响应的快速傅里叶变换。根据信道的频率响应，如果信道的带宽相对于频率变化较大，则信道为频率选择性信道；如果信道的带宽相对于频率变化较小，则信道为非频率选择性信道/平坦衰落信道。

• 时域拓展
  由于无线信道中的多径传播，使得沿着不同路径传播的信号到达接收机的时间不同，在接收机侧会观察到同一个符号表征的信号在时域上发生延展，称为时域拓展(time dispersion)。由于多径效应的影响，信号到达时间会产生变化。由于到达时间的变化，同一载波内的符号之间会相互干扰，形成符号间干扰（ISI）。

• 相干带宽
  无线信道频率响应能够保持相对不变的最大带宽称为相关带宽/相干带宽(\(B_{coh}\)，coherence bandwidth)。50%相干带宽表示为：
  \[B_{coh}≈\frac{1}{5σ_τ}\] \(σ_τ\)表示功率时延谱（\(P(τ)=∑_{t_i=0}P(t_i)δ(τ-t_i)\)）的标准差：
  \[σ_τ=\sqrt{\frac{1}{P_{av}}∑(τ-μ_τ)^2P(τ)}\]
  \[μ_τ=\frac{1}{P_{av}}∑τP(τ)\]

当信道的符号带宽\(W\)大于等于相关带宽\(W≥B_{coh}\)时，信道称为频率选择性信道。
当信道的符号带宽\(W\)远远小于相关带宽\(W<<B_{coh}\)时，信道称为频率平坦信道。