05.图像压缩
本文最后更新于 2025年6月4日 晚上
图像压缩
概述
问题动机
使用图像压缩的动机有两点:
- 如果不使用图像压缩技术,那么图像和视频文件所包含的信息量是相当巨大的。
以一部分辨率为720P(1280px × 720px),24fps,时长1小时的彩色8bit电影计算,其包含的信息量为:\(1280px × 720px×3×8bit×24fps×3600s=1,911,029,760,000bit=1,779.78515625MB\)
- 图像本身可能有较多的冗余信息。
下面三个例子说明了三种图像常见的冗余信息:- 编码冗余(encoding redundancy):这张256px × 256px的图像中仅存在四种不同值的像素。如果选用通用的8bit编码方式,那么有251个灰度值都从未使用过。

- 空间冗余(spatial redundancy):这张256px × 256px的图像中每一竖列所使用的像素都是相同的,这意味着相同的灰度值序列被重复使用了256次。

- 无关信息(irrelevant information):下图中的所使用的像素其灰度值差别仅有±1,肉眼很难分辨出它们之间的差别。

- 编码冗余(encoding redundancy):这张256px × 256px的图像中仅存在四种不同值的像素。如果选用通用的8bit编码方式,那么有251个灰度值都从未使用过。
基于上述的两点原因,图像处理中需要图像压缩技术通过减少图像的冗余信息来降低图像文件的信息量。
压缩过程
如果将图像表示为一个灰度值函数,自变量为空间位置\(f(x,y)\),图像压缩(compression)技术可以通过对图像编码和解码来实现对信息的压缩,以便将图像信息发送给接收方。接收方利用解压缩过程(decompression)将比特流解码为图像,再使用反映射将图像进行复原。整个过程如下图所示。
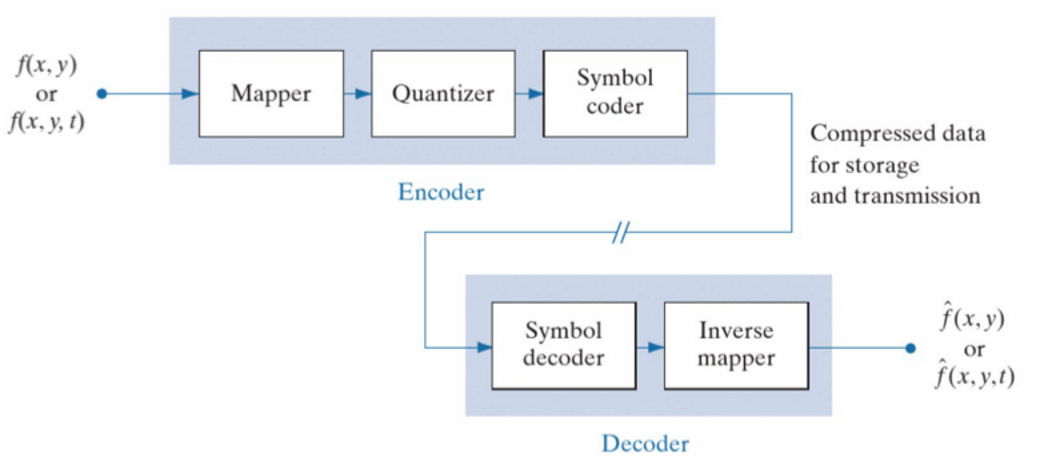
可以发现复原后的图像\(\hat{f}(x,y)\)并非和原图像\(f(x,y)\)一模一样,这两者之间的差异可以通过均方差(mean square error, MSE)来衡量:
\[MSE=\frac{1}{N_{Pixels}}∑_{(x,y)}(\hat{f}-f)^2\] 其中\(N_{Pixels}\)表示像素个数。
在量化阶段,量化将灰度值转换为可以传输的比特信息,这个过程中通过引入量化误差来实现对于图像的压缩。量化过程是图像压缩过程中信息损失最多的环节。
量化之前的映射过程的目的是通过使用一些变换函数尽可能地减小原图和复原图像之间的均方差。经过映射后的图像通过量化和传输时的信息损失更少。
JPEG
图像压缩的编码方式需要形成全球通用的标准,如此各种图像和视频才可以在全球范围内传播和接收。下图展示了目前较为常用的图像和视频压缩标准:
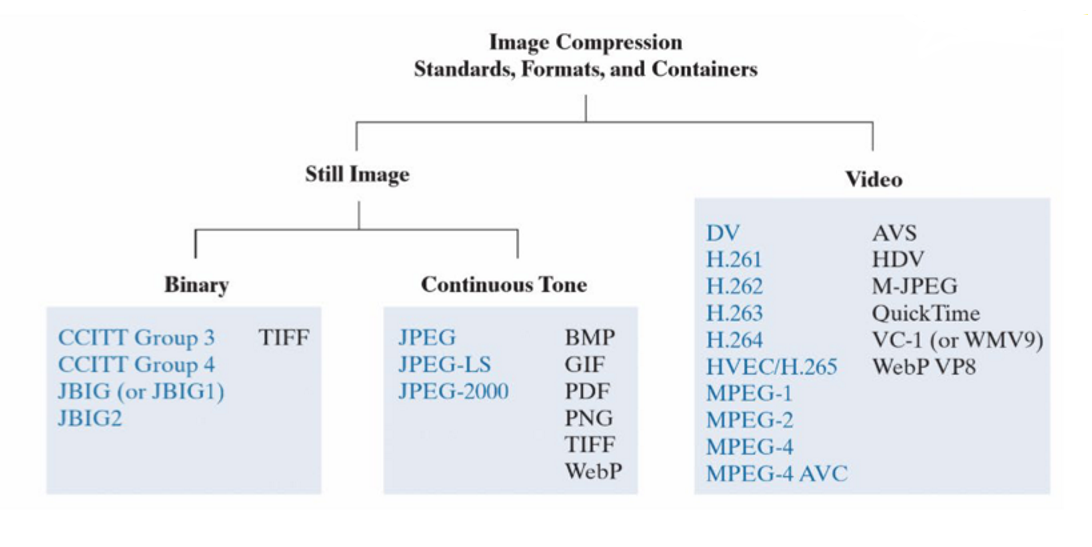
JPEG(Joint Photographic Experts Group)是其中的一种国际标准,其图像压缩和解压缩的过程如下图所示:
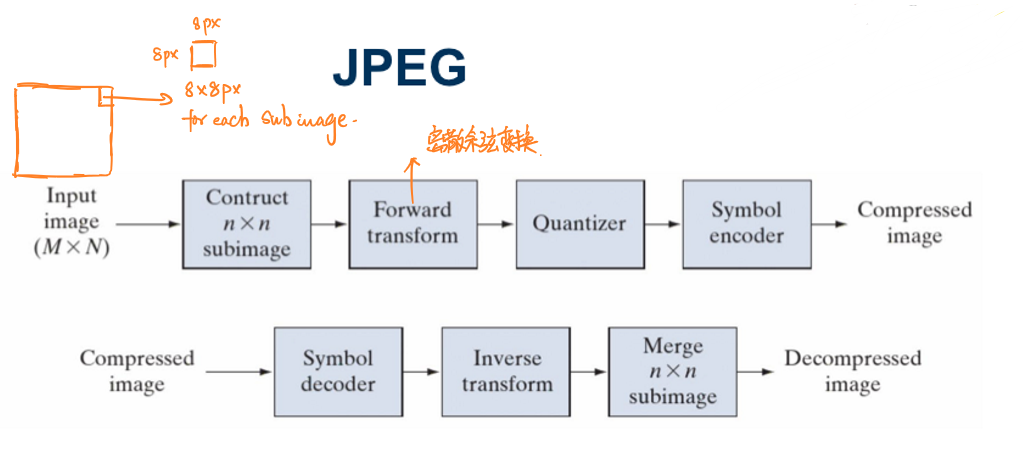
JPEG会首先将一整个图片分为8px × 8px的子图,然后再分别对每一张子图做相应的处理。对于彩图,JPEG会将图像拆分为\([R,G,B]\)三通道,然后映射为\([Y,CB,CR]\)三通道。
\([Y,CB,CR]\)色彩空间中,\(Y\)为颜色的亮度(luma)成分、而\(CB\)和\(CR\)则为蓝色和红色的浓度偏移量成份。
子图通过前向变换(Forward transform)(主要是离散余弦变换)实现映射,每一张8px × 8px进行量化后会生成仅生成一个元素,然后进行编码。
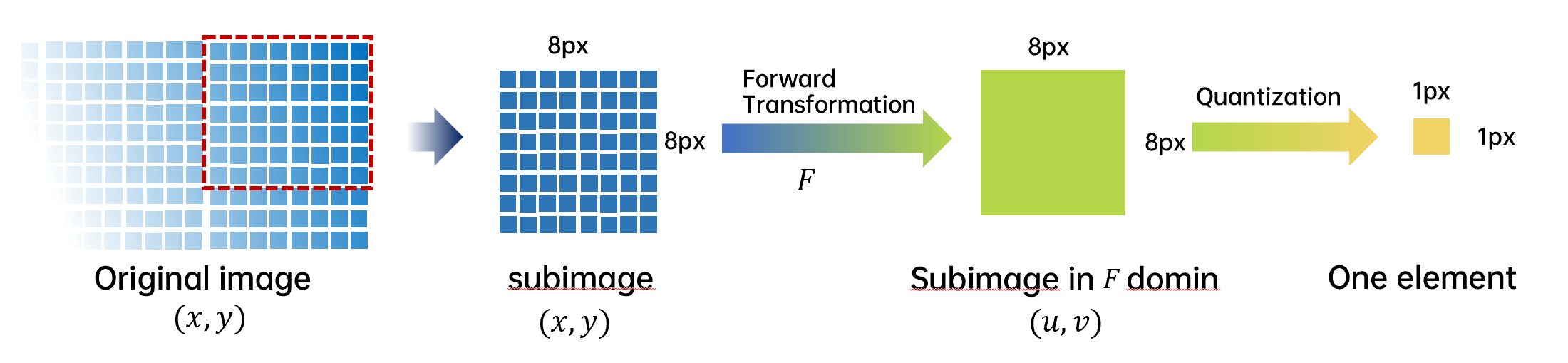
JPEG标准中子图采用8px × 8px大小与JPEG中采用的离散余弦变换的性质(见后文)有关:
使用更小的子图会导致分组增多从而导致离散余弦变换的图像质量下降。越大的子图越不容易满足马尔科夫条件,同时更大的子图计算量也更多。
前向变换
K-L变换
K-L变换(Karhunen-Loève Transform)是一种图像处理常用的变换。
K-L变换以矢量信号\(X\)的协方差矩阵\(Ф\)的归一化正交特征矢量\(q\)所构成的正交矩阵\(Q\),来对该矢量信号\(X\)做正交变换: \[Y=QX\] 其中\(Q^TQ=I\)。
经过K-L变换后提取出来的一个元素经过复原后的图像相比于直接从子图上提取一个像素得到的均方差要小的多。
此外,从定义上可以看出K-L变换的算子\(Q\)是由原图\(X\)决定的,这样的缺点是对于每一张图片都需要生成一个特定的K-L变换算子\(Q\)。很显然这样的变换并不是通用的解决方案。
离散余弦变换
离散余弦变换(discret cosine transformation,DCT)是JPEG标准中采用的前向变换方法。相比于K-L变换,离散余弦变换的算子是通用算子,与原图独立。但是复原图像的均方差相比于使用K-L变换得到的复原图像较大,不过仍然在可以接受的范围。
离散余弦变换的公式可以表示为:
\[T(u,v)=∑_{x=0}^{n-1}∑_{y=0}^{n-1}f(x,y)r(x,y,u,v)\] 其中\(f(x,y)\)是原图像,\(r(x,y,u,v)\)称为变换系数(transformation coeffients)。
相应的,反离散余弦变换(inverse discret cosine transformation)公式为:
\[F(x,y)=∑_{u=0}^{n-1}∑_{v=0}^{n-1}T(u,v)S(u,v,x,y)\] 对于离散余弦变换及其反变换,它们的变换系数是相同的:
\[r(x,y,u,v)=S(u,v,x,y)\] 这个变换系数的具体表达式为:
\[r(x,y,u,v)=α(u)α(v)cos\left[\frac{(2x+1)uπ}{2n}\right]cos\left[\frac{(2y+1)vπ}{2n}\right]\] 其中,
\[α(u)=\begin{cases}
\sqrt{\frac{1}{n}},u=0\\
\sqrt{\frac{2}{n}},u≠0\\
\end{cases}\]
需要注意的是当信号具有接近马尔科夫过程(Markov processes)的统计特性时(这样的条件又被称为马尔科夫条件),离散余弦变换的去相关性接近于K-L变换。此时离散余项变换的作用相当于K-L变换。
另外,相比于快速傅里叶变换(fast fourier transformation, FFT),离散余弦变换可以通过反转信号达到变换后信号是原信号周期的两倍,如此避免了快速傅里叶变换中可能出现的间断点。离散余弦变换后子图之间的间隔更加平滑。
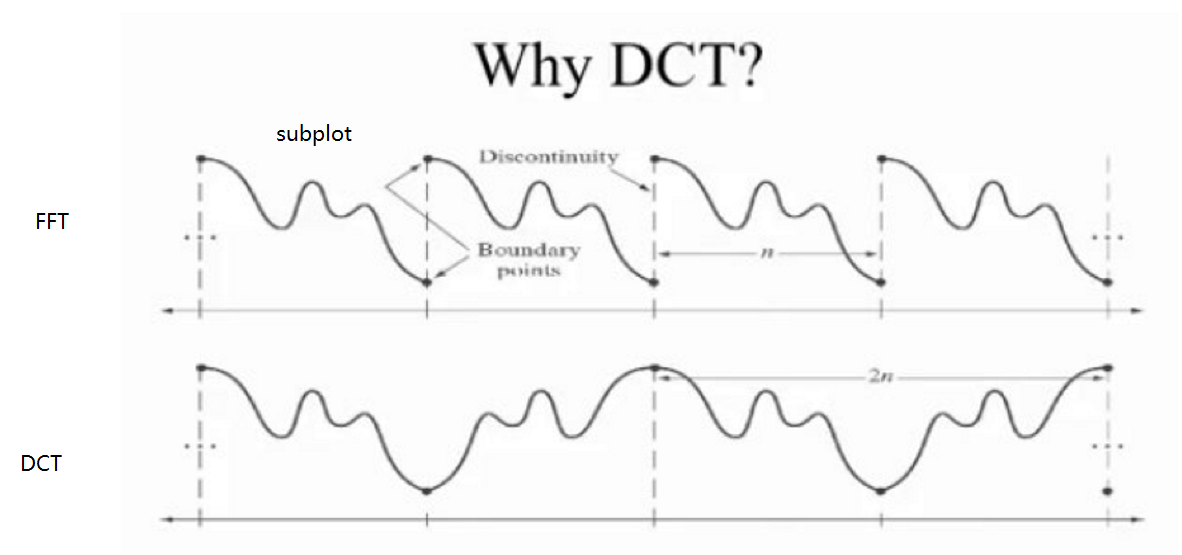
实际运用时,由于已经明确每次进行离散余弦变化的矩阵大小为8×8,故这里不再采用上述方法进行离散余弦变换,而是利用离散余弦变换矩阵实现变换以降低运算量。
离散余弦变换矩阵计算公式为:
\[T_{ij}=\begin{cases}
\frac{1}{\sqrt{M}},i=0,0≤j≤M-1\\
\frac{2}{\sqrt{M}}cos\frac{π(2j+1)i}{2M},1≤i≤M-1,0≤j≤M-1
\end{cases}\] 因此可以得到8×8的变换矩阵为:
\[T=\begin{bmatrix}
0.35355&0.35355&0.35355&0.35355&0.35355&0.35355&0.35355&0.35355\\
0.49039&0.41573&0.27779&0.09755&-0.09755&-0.27779&-0.41573&-0.49039\\
0.46194&0.19134&-0.19134&-0.46194&-0.46194&-0.19134&0.19134&0.46194\\
0.41573&-0.09755&-0.49039&-0.27779&0.27779&0.49039&0.09755&-0.41573\\
0.35355&-0.35355&-0.35355&0.35355&0.35355&-0.35355&-0.35355&0.35355\\
0.27779&-0.49039&0.09755&0.41573&-0.41573&-0.09755&0.49039&-0.27779\\
0.19134&-0.46194&0.46194&-0.19134&-0.19134&0.46194&-0.46194&0.19134\\
0.09755&-0.27779&0.41573&-0.49039&0.49039&-0.41573&0.27779&-0.09755\\\end{bmatrix}\] 实际变换过程即用原图\(f(x,y)=I\)与该矩阵和其转置矩阵相乘:\(TIT'\)即可得到变换后的结果。
实施二维离散余弦变换可将图像的能量集中在极少的几个系数之上,其他系数相比于这些系数的绝对值要小很多,这些系数大都集中在左上角。
同时通过观察变换系数的结构可以发现,项\(cos\left[\frac{(2x+1)uπ}{2n}\right]cos\left[\frac{(2y+1)vπ}{2n}\right]\)中\(u,v\)的值越小、这两项的角频率越小、频率越低,因此图像中\((u,v)\)越小的左上角称为低频分量区,这个区域中集中了图像中大部分的信息。而右下角为\((u,v)\)最大的位置,该区域为高频分量区,图像的高频分量中只包含了图像的细微的细节变化信息,而人眼对这种高频成分的失真不太敏感,所以,可以考虑将这一些高频成分予以抛弃,从而降低需要传输的数据量。
Zigzag扫描排序
内存里所有数据都是线形存放的,如果一行行地存放这64个离散余弦变换的系数,每行的结尾的点和下行开始的点就没有什么关系,所以JPEG规定按如下图中的数字顺序依次保存和读取64个离散余弦变换的系数值。
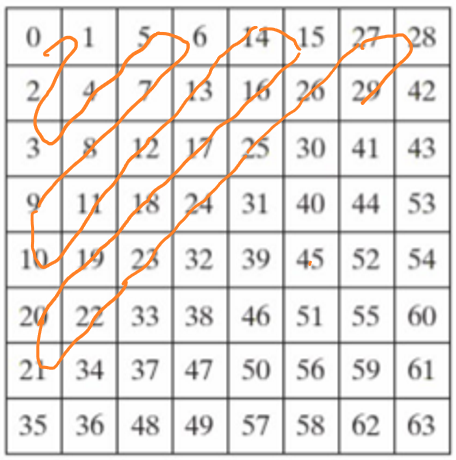
这样数列里的相邻点在图片上也是相邻的了。不难发现,这种数据的扫描、保存、读取方式,是从8×8矩阵的左上角开始,按照英文字母Z的形状进行扫描的,一般将其称之为Zigzag扫描排序。
量化
量化过程是JPEG标准中信息损失最大的部分。JPEG中量化的目的是为了大幅度的压缩图像大小,同时保证图像的质量,即重建后的图像仍然保留了原图中的大部分信息。
根据离散余弦变换的性质可知,变换后图像大部分的信息将被集中在左上角,因此,在量化过程中,图像的左上角将被使用更高的精度(更多的比特)进行量化,下图展示了JPEG量化过程中为子图中每个像素量化所使用的比特数量的分配。
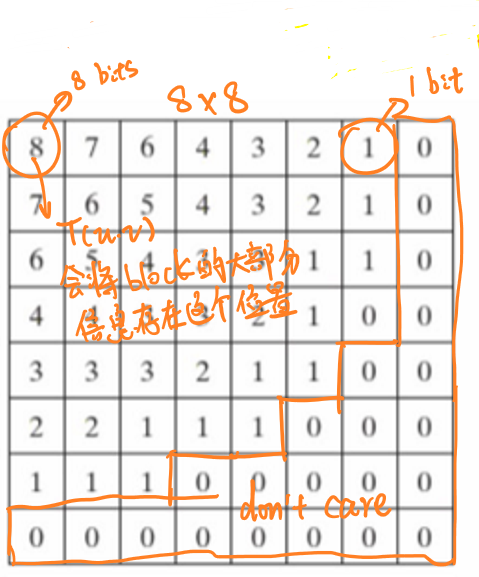
JPEG的量化过程采用的阈值量化,即在不同的阈值范围内量化值是不同的。简单来说,量化的公式可以表示为:
\[\hat{T}(u,v)=[\frac{T(u,v)}{C}]_{round}×C\] 其中\([·]_{round}\)表示取整,\(C\)是设定好的阈值。
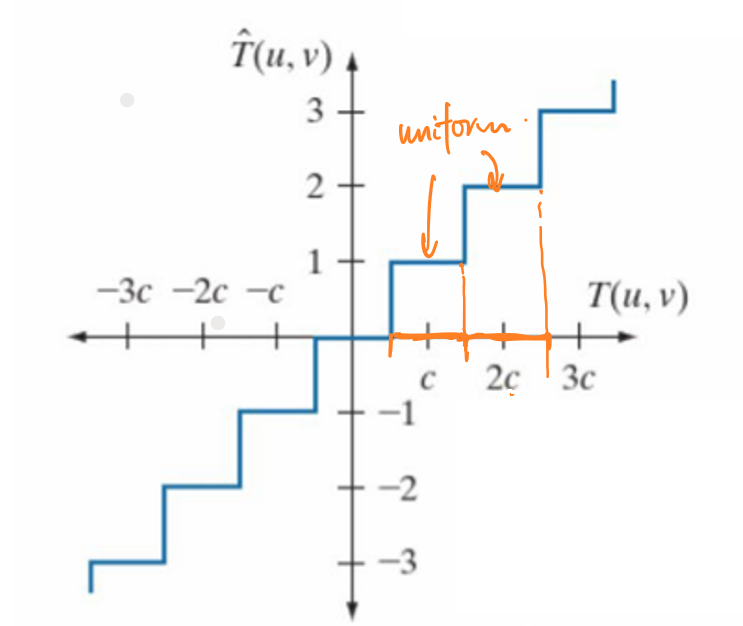
对于不同位置的像素,JPEG使用了不同的量化阈值。左上角的阈值要小于右下角的阈值,以便更好地捕捉子图中左上角的信息。
整除的过程本身是均匀的,但是通过设置不同的量化阈值将左上角和右下角的差异拉开,也便于之后进行霍夫曼编码(见后文)。
实际上,JPEG的量化过程会事先建立一个8×8的量化表,将变换后的矩阵中各元素除以对应量化表中的元素,并对结果舍入取整(取最接近的整数),以便于执行最后的编码。
下图展示了JPEG标准中规定的灰度量化表:
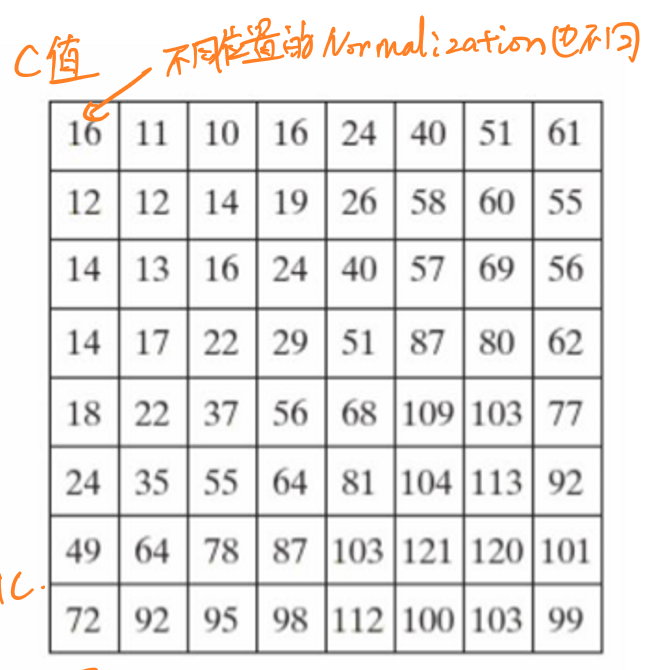
经过量化阶段之后,所有的数据只保留了整数近似值,也就再度损失了一些数据内容。
对于彩图,由于对亮度和色度的精度要求不同,分别对亮度和色度采用不同的量化表。前者细量化,后者粗量化。
霍夫曼编码
JPEG中采用的是霍夫曼编码(Huffman coding),这种编码方式可以极大地减少信息冗余,增大信息密度。
简单来说,在信息论中信息的平均编码长度\(avgL\)可以表示为每个值\(r_i\)出现的频率\(p_{r_i}\)与对应比特长度\(L_i\)的乘积之和:
\[avgL=∑_ip_{r_i}×L_i\] 霍夫曼编码按照每个像素值(灰度值或者RGB值)在图像(子图)中出现的频率来为每个像素值确定其编码的长度:像素值出现的频率越低,那么其对应编码的长度越长。 如此,信息的编码长度会大幅度缩短。
霍夫曼编码的过程分为两步,当每个像素值的出现频率被确定后,按照频率大小为其排序。接着按照排序结果为每个像素值赋予相应的编码长度和比特值。每一个频率\(P_r\)对应一种比特长度\(L_r\),并且频率\(1-n×P_r\)(\(n\)代表具有\(P_r\)的像素值个数)所对应的比特长度应当为\(L_r+\sqrt{n'+1}\)(\(n'\)为下一个频率对应的像素值个数)。

下图展示了使用霍夫曼编码的一个例子:
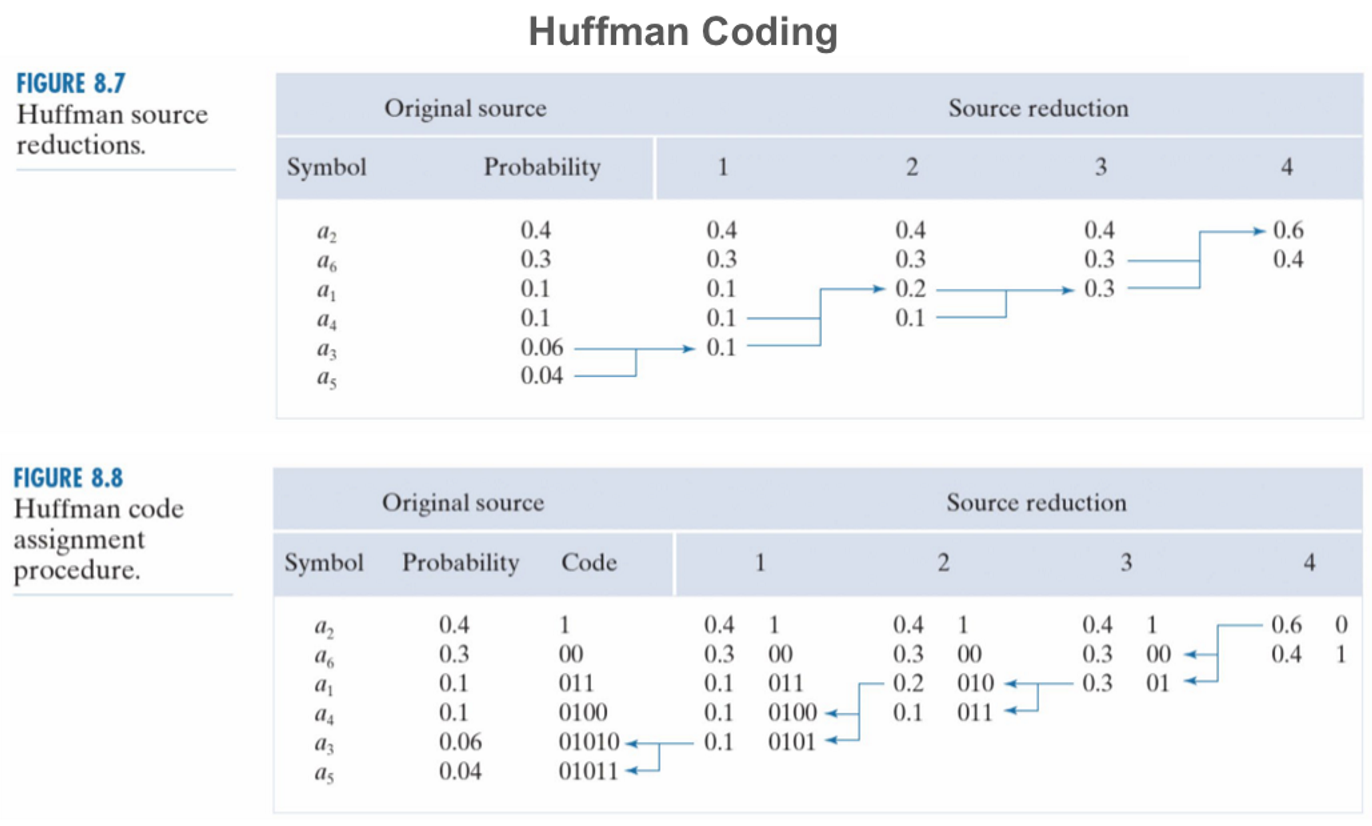
霍夫曼编码的特点是:
- 非对称编码 (asymetric)
不同值对应的编码和解码所占用的资源大小不同。
- 前缀无关编码 (prefix-free) 任何一个码字都不是其它码字的前缀的编码。