06.图像增强

图像增强

图像处理的本质是对图像矩阵进行一些数学操作，图像处理主要有两大类技术：点处理(point processin)和相邻处理(neighborhood processing)，此外还有直方图均衡和边缘检测等操作。

点处理

点处理是像素点到点的变换，其影响仅限于单个的像素。图像上一个像素值\(r(x,y)\),经过处理\(s(x,y)=T(r(x,y))\)后，得到同一位置的像素\(s(x,y)\)。
注意： 1. \((x,y)\)表示坐标。 2. 不同的图像处理库坐标系统的原点设置不同，\(y\)的取值设定也不同。
3. \(T\)通常只能是单调（通常是单调递增）的函数。

点处理的几个特性：
- 点处理的影响仅限于单个的像素点。
- 点处理不会改变像素的位置。

常见的点处理变换

阈值变换

阈值变换(thresholding)可以表示为：
\[s=\begin{cases} 0, r≤k\\ 255,r>k \end{cases}\] 其中\(k\)点称为阈值，高于阈值的像素将会被强化为近白色/白色的像素值，低于阈值的像素值将被弱化为近黑色/黑色的像素值。

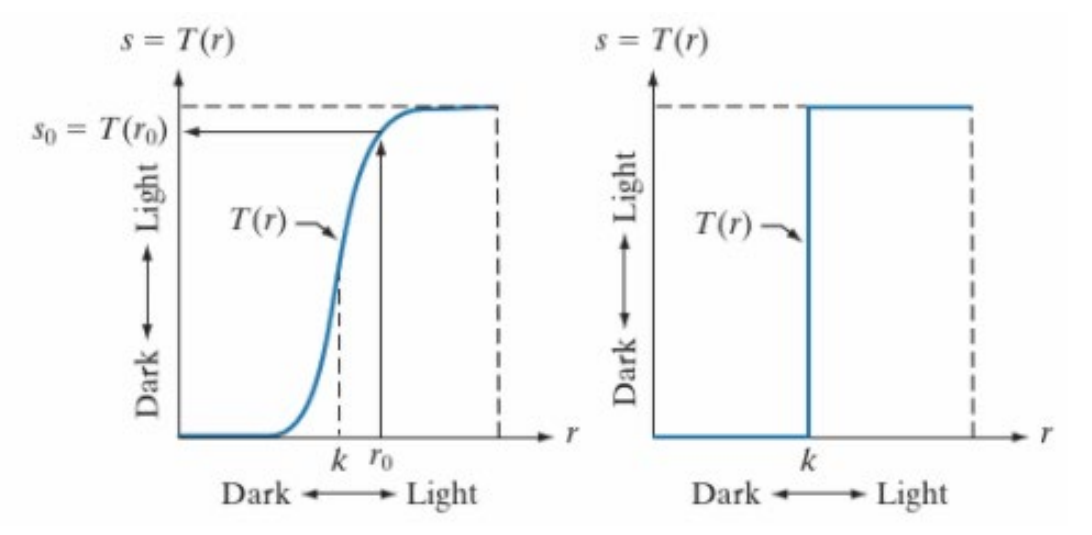
阈值函数可分为两种：软阈值函数（左图）和硬阈值函数/二值化函数(Hard thresholding/Binarization，右图)，它们的作用都是将像素转换成黑白像素。

对数变换

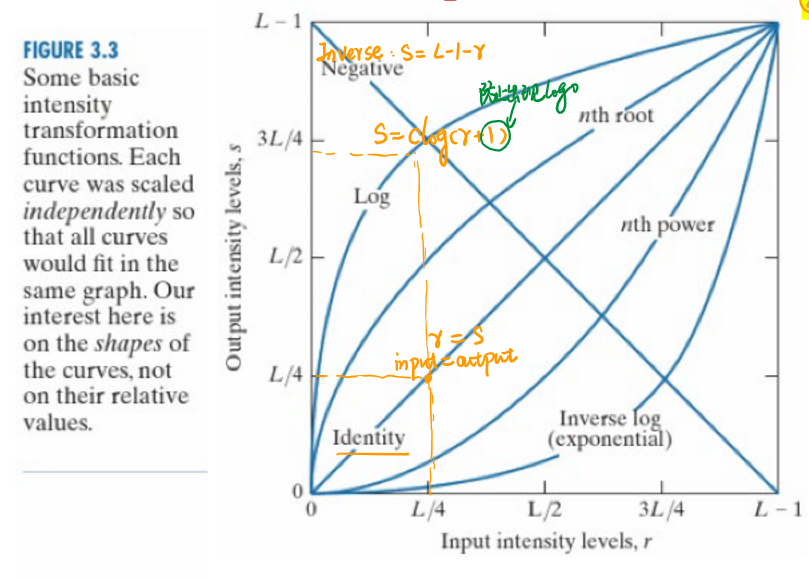
对数变换的表达式为：
\[s=clog(1+r)\] 对数变换能够扩展低灰度值（突出过暗区域的细节）而压缩高灰度值（突出过曝区域的细节），从而增强图像的清晰度。

幂变换

幂变换的表达式为： \[s=cr^γ\] 其中\(γ\)是幂指数。

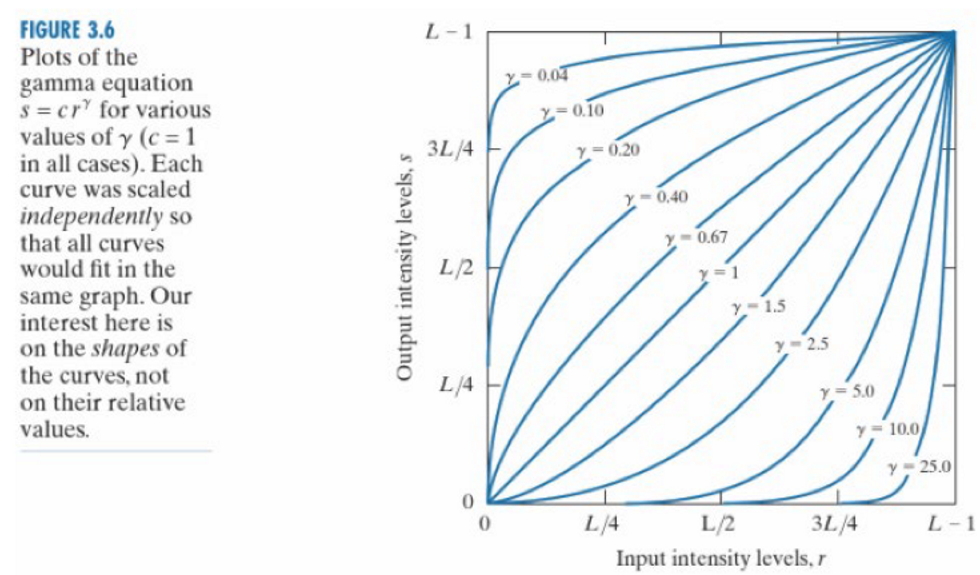
幂变换用于调整图像整体的明暗关系。当\(0<γ<1\)时，图像整体的暗部被加强；\(γ>1\)时，图像整体的亮部被加强。

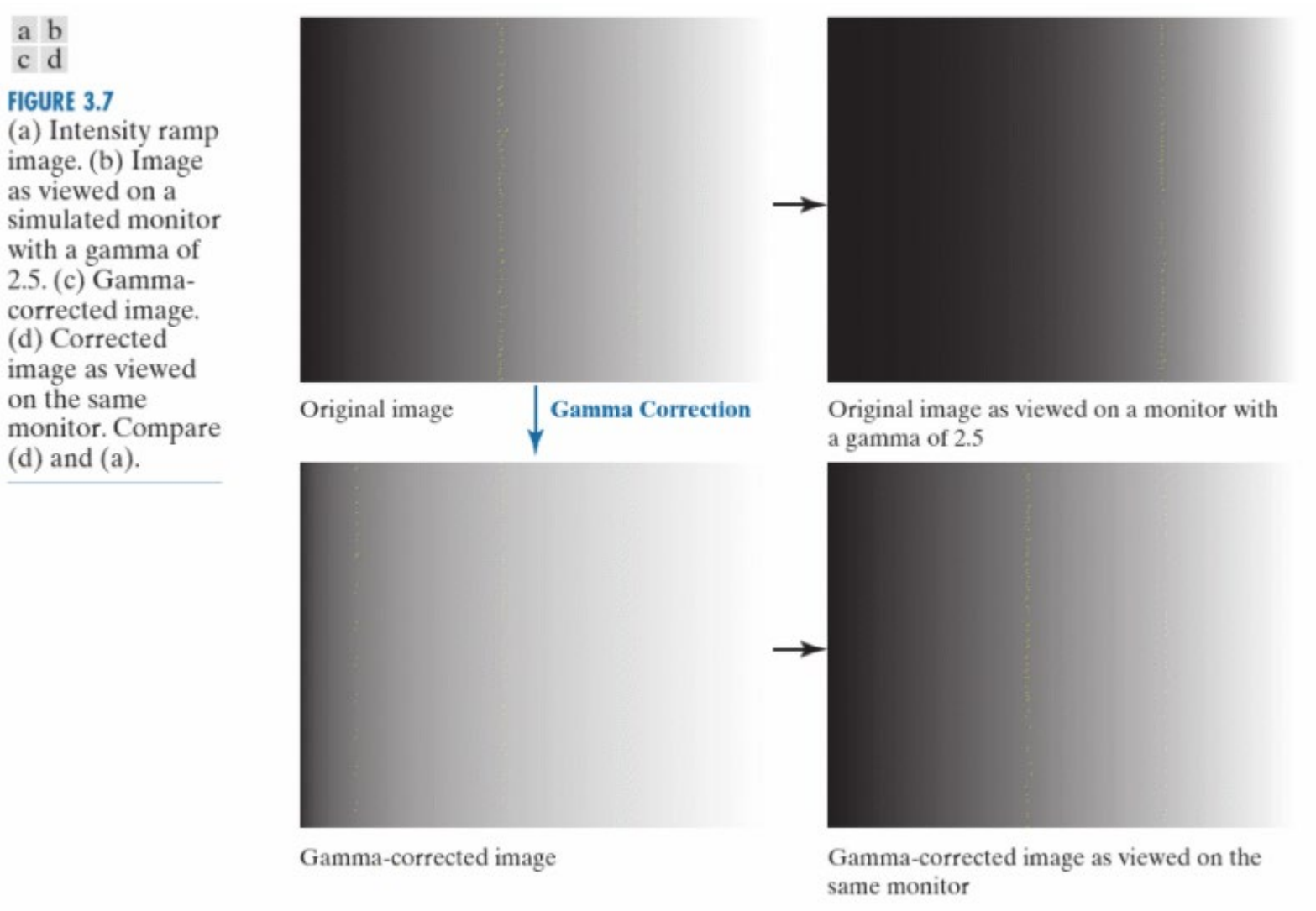
幂变换又被称为伽马变换。显示器中的伽玛校正(Gamma Correction)即得名于此，可以调整该值使得显示器整体偏亮或偏暗。 当\(0<γ<1\)时，显示器偏暗，\(γ<1\)时，显示器偏亮。

反转

反转(inverse)的表达式为：
\[s=L-1-r\] \(L\)表示最大的像素值。
反转的作用是作用是将像素值进行颠倒：白色变为黑色，黑色变为白色。

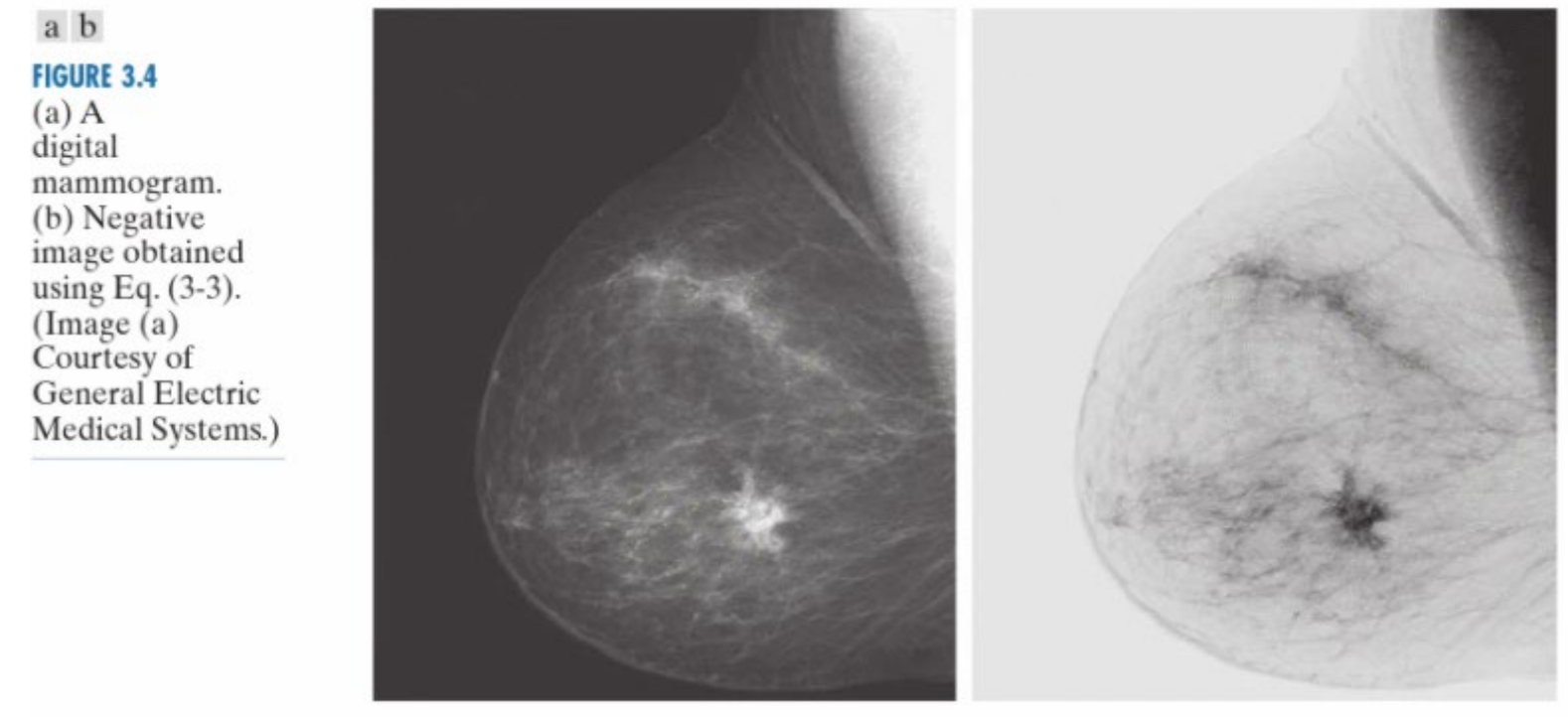
反转后的图像可以使用上述式子再对图像进行复原，复原后的图像将和原图完全一样。反转处理不会破坏图像信息。

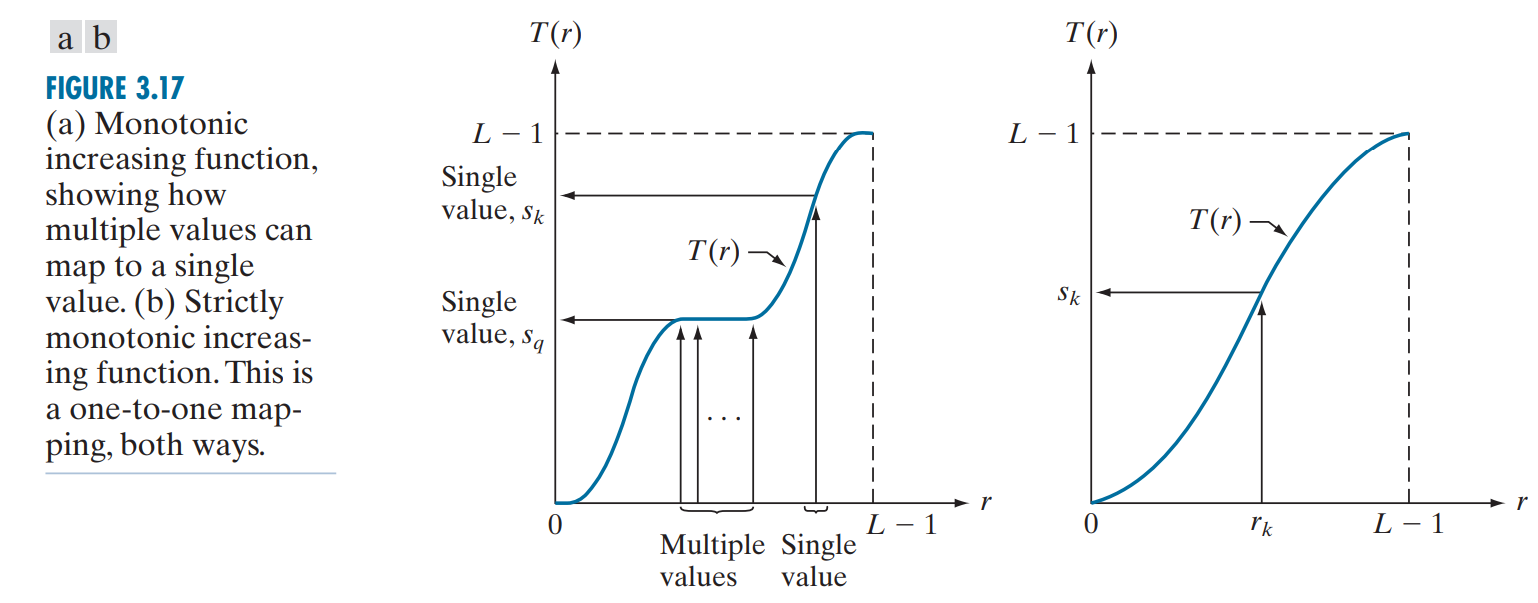
进一步地，可以发现，对于图像的点处理：\(s=T(r)\)，当且仅当\(T(·)\)是一个严格单调的函数时，原图像中的像素可以和处理后的图像中的像素一一对应，如此只需要使用\(T(·)\)的反函数\(T^{-1}(·)\)就能够将图像从处理后的状态恢复到原图，且恢复过程没有任何损失。

线性分段处理

线性分段处理(linear piecewise)可以分区域对不同的灰度区域实现不同的映射，进而选择性地增强图像的细节。如下图例子中只有处于中等灰度值的像素被加强。

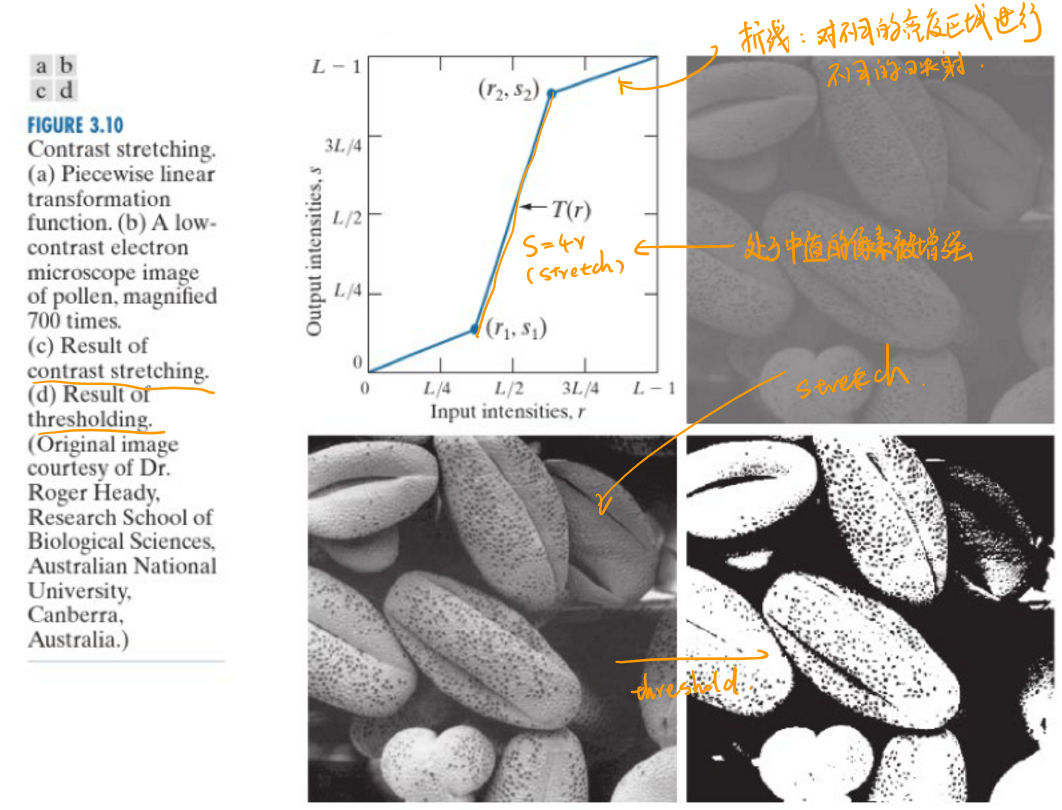
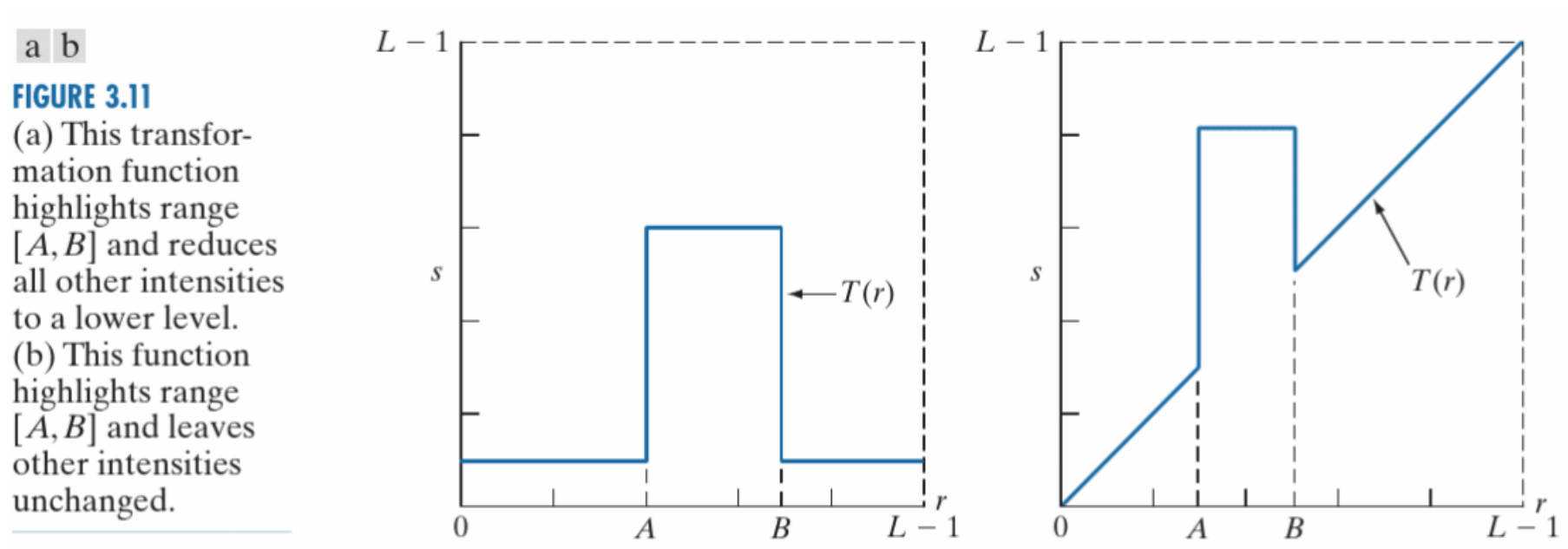
局部增强可以选择在增强目标灰度区域的同时减弱其他灰度区域的像素值，也可以选择让其他灰度区域的像素值保持不变。

亮度直方图

亮度直方图(histogram)的横轴是像素值，纵轴是该像素值对应的像素点个数，它反映了图像整体的像素分布情况。
如果直方图在白色区域内比较集中，图像偏亮，直方图窄黑色区域内比较集中，图像偏暗。图像在直方图上的最大分布范围（即横轴的宽度）称为对比度(Contrast)，直方图窄的图像对比度低。通常情况下，对比度越高图像越清晰。

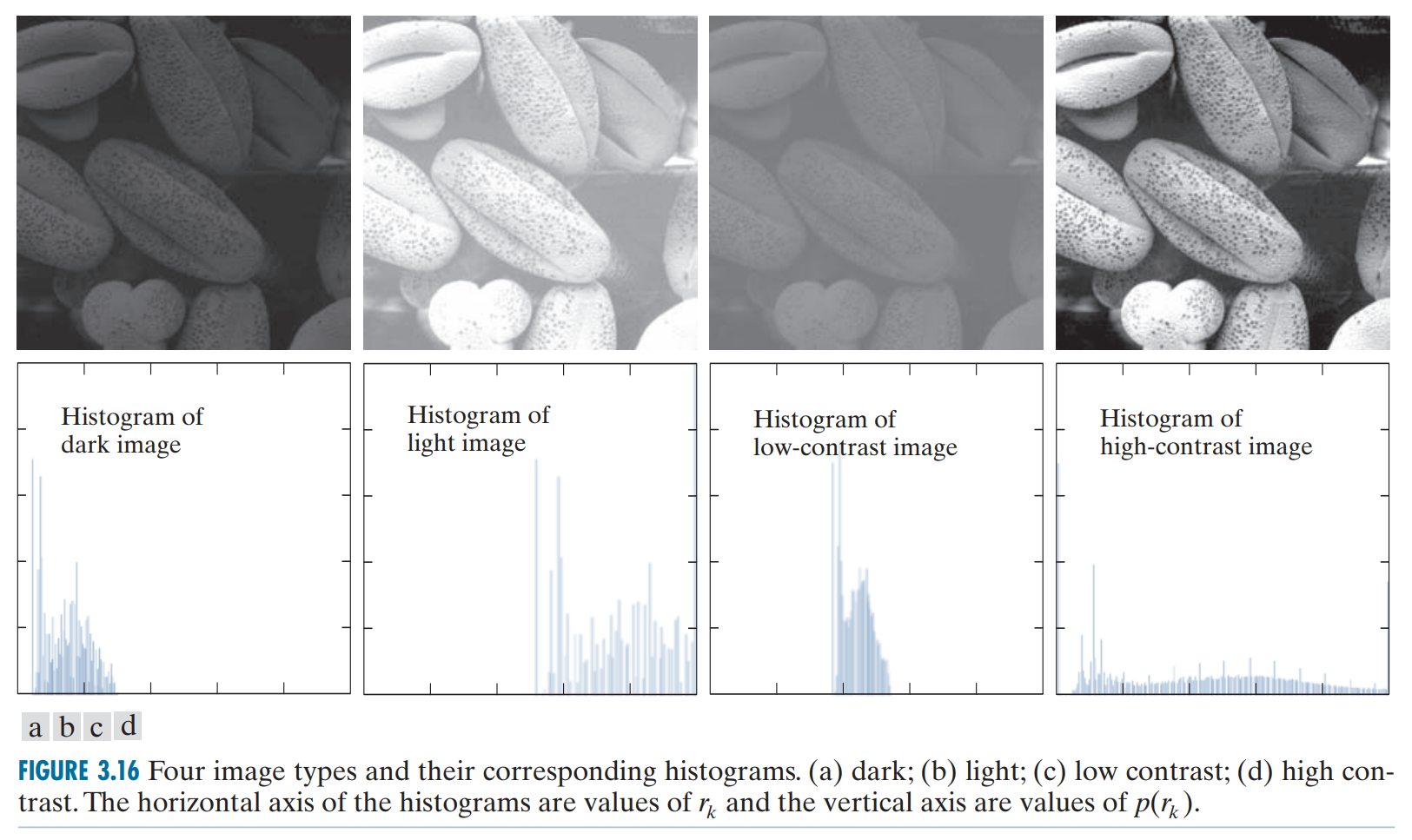
同时，也可以通过上图发现，图像在直方图上的分布越均匀，整个图像的明暗表现越好，同时图像的细节也得到更好的表现。

下面的MATLAB程序展示了如何将图像进行反转并得到反转前后的图像的亮度直方图。

I = imread('test.jpg'); % load image
figure(1); imshow(I); % display original image
figure(2); imhist(I); % show the histogram of I

figure(3); imshow(255-I); % inversed image
figure(4); imhist(255-I); % inversed histogram

% histogram equalization
K = histeq(I);
figure(5); imshow(K);
figure(6); imhist(K);

直方图均衡

直方图均衡(historgram equalization)是一种用于增强图像对比度的同时均衡图像亮度的方法，其目的是为了尽可能地将图像像素在直方图上的分布改变为均匀分布。直方图均衡是一种点处理。

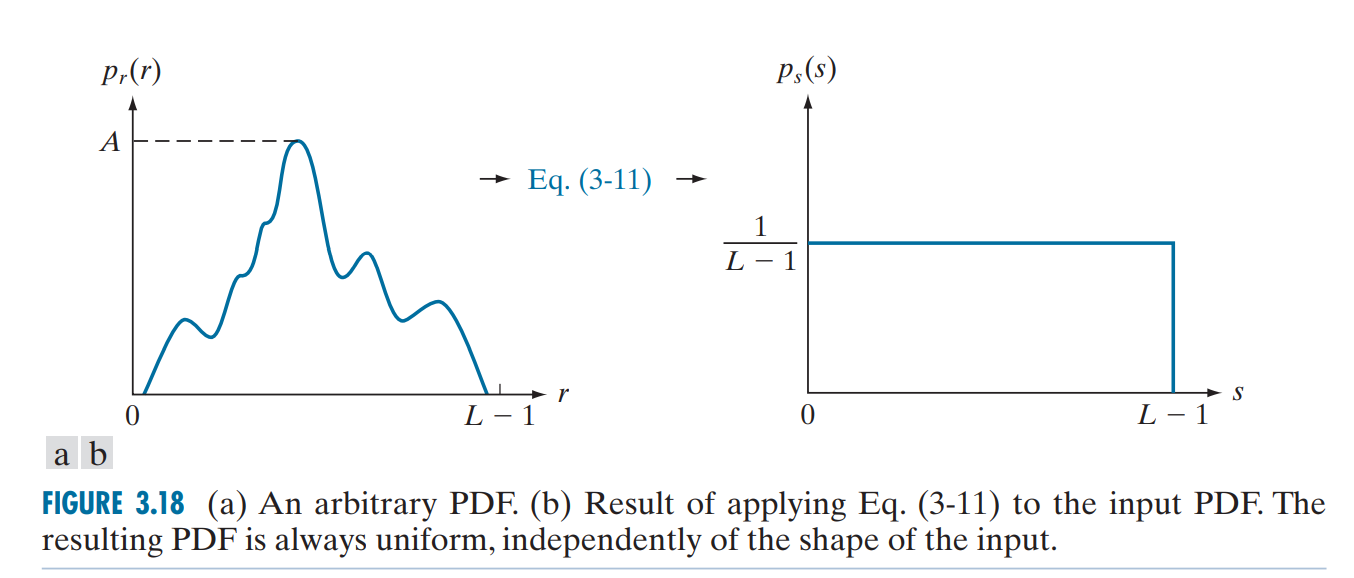
下图左图为原图，右图为经过直方图均衡后的图像以及它们的直方图。

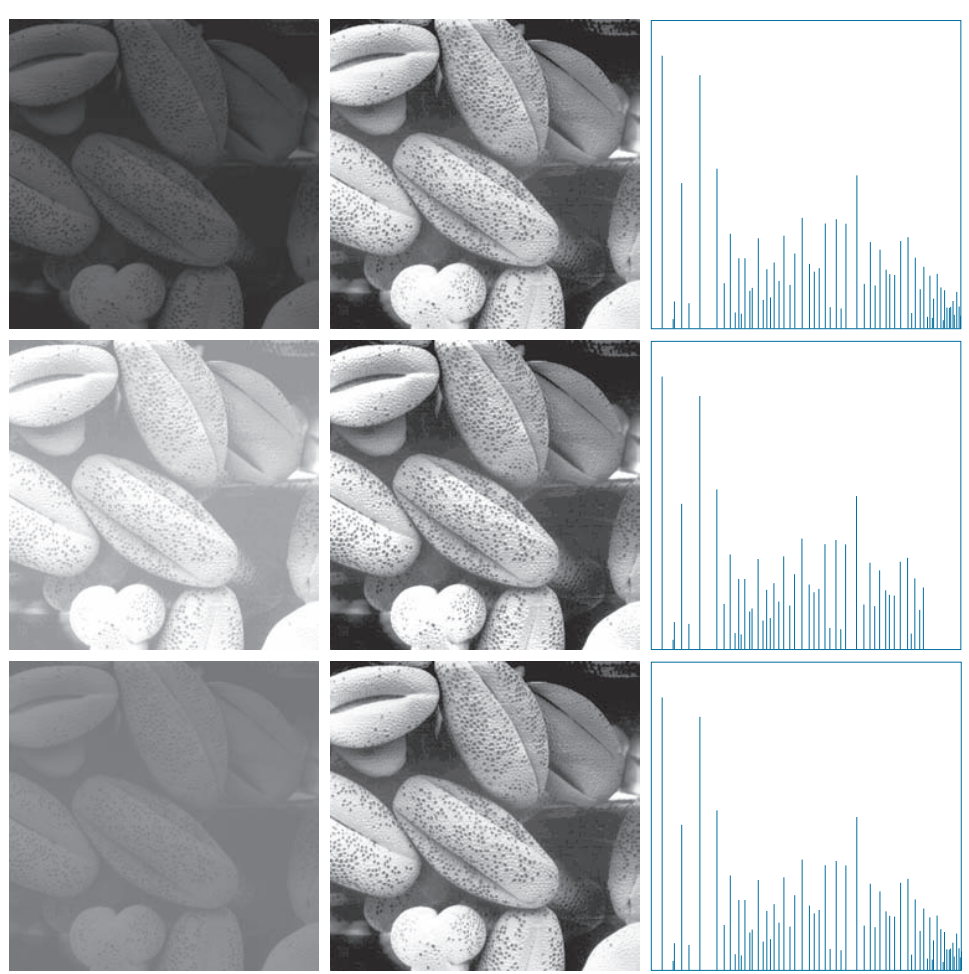
直方图可以视为反映了每一个像素值在整个图像的占比关系（\(\frac{n_w}{n}\)，n表示图像像素点总数，\(n_w\)表示像素值为w的像素点数量），因此整个直方图可以被概率分布函数化：
\[p_r(w)=p(r=w)=\frac{n_w}{n},w=0,1,...,255\]
定义直方图均衡变换：
\[s=T(r)=(L-1)\int_0^rp_r(w)dw\] 其离散形式为：
\[s=T(r)=(L-1)\sum_{w=0}^rp_r(w)\] 使得:
\[P_s(s)=P_r(r)|\frac{dr}{ds}|=\frac{1}{L-1}\] 由于\(w\)并不是连续的，因此最终的直方图并非是完全扁平的矩形。

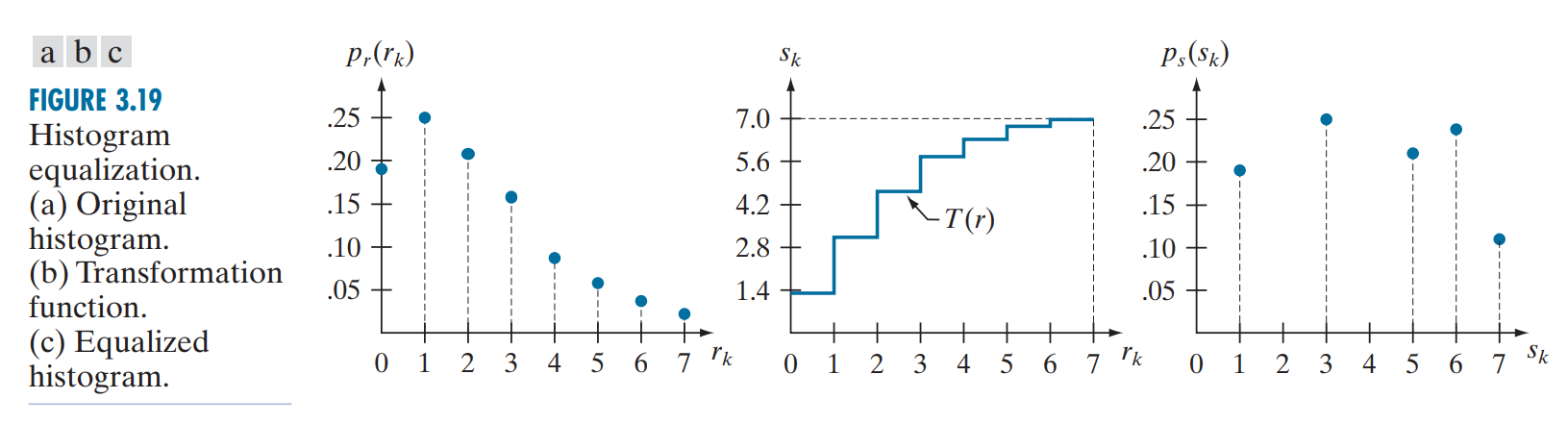
证明：当\(s=T(r)=(L-1)\int_0^rp_r(w)dw\)时，对等式两边求导：
\[\begin{aligned} \frac{ds}{dr}=\frac{dT(r)}{dr}&=\frac{d[(L-1)\int_0^rp_r(w)dw]}{dr}\\ &=(L-1)\frac{\int_0^rp_r(w)dw}{dr}\\ &=(L-1)P_r(r) \end{aligned}\] 带入\(P_s(s)=P_r(r)|\frac{dr}{ds}|\)，有：
\[P_s(s)=P_r(r)|\frac{dr}{ds}|=\frac{1}{L-1}\]

局部增强

对图像局部的一些像素群（例如以某个像素为中心\(9 × 9\)或\(3 × 3\)的像素）应用直方图均衡的方法称为局部增强(local enhancement)。

直方图匹配

直方图匹配(historgram matching)的是将图像的直方图尽可能地接近设计好的亮度直方图的一种方式。其基本思想是：理论上原图的亮度直方图和设计好的亮度直方图都可以通过直方图均衡得到相同的均匀分布的直方图，因此只需要将原图进行一次直方图均衡，再使用一次设计直方图的反直方图均衡即可得到设计好的直方图。

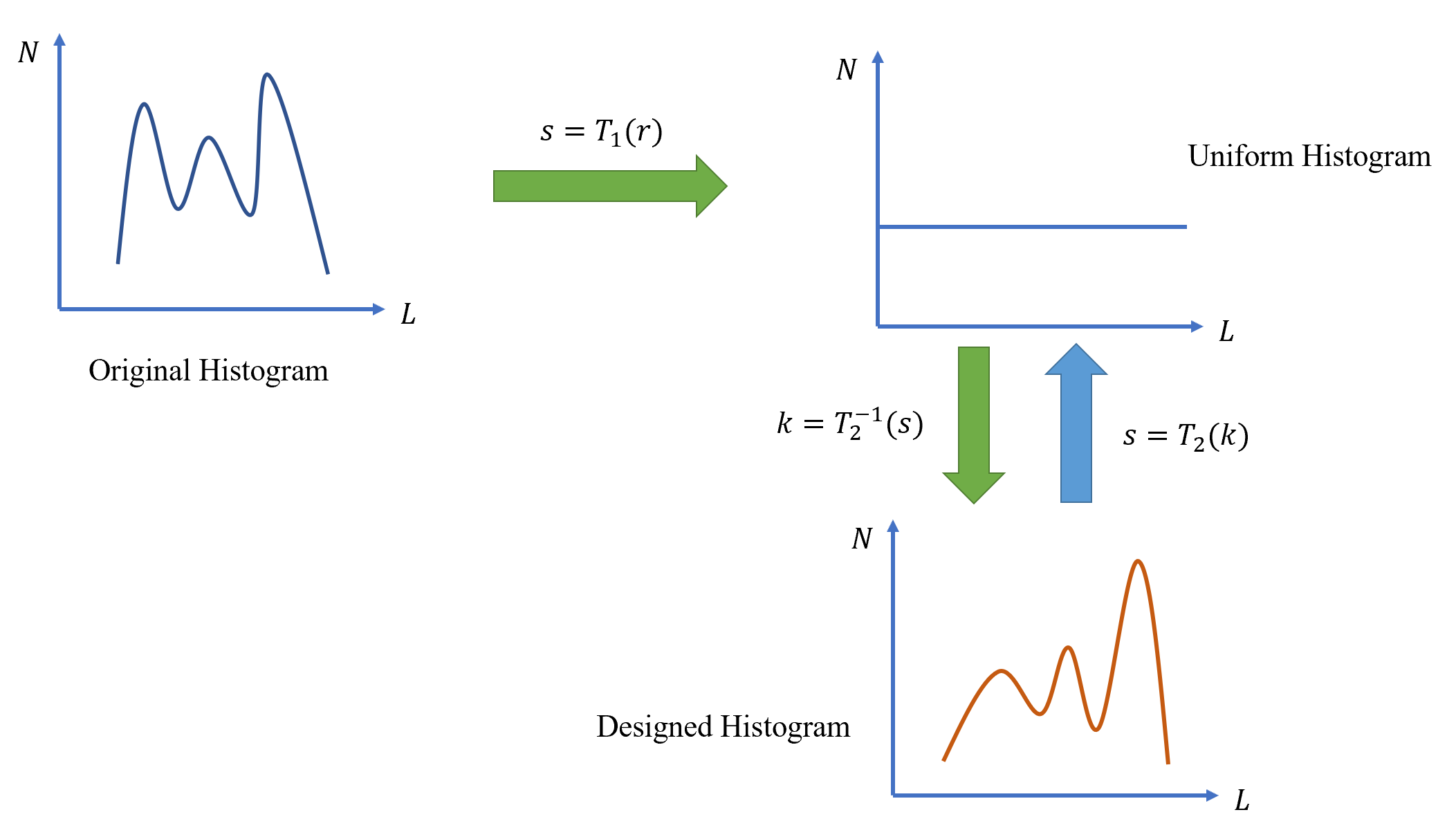
设原图为\(R\)，有直方图均衡\(s=T_1(r)\)。
设设计的直方图对应图像为\(K\)，有直方图均衡\(s=T_2(k)\)，求得反函数\(k=T_2^{-1}(s)\)，那么有原图到设计图的直方图匹配：
\[k=T_2^{-1}(s)=T_2^{-1}(T_1(r))\]

直方图匹配的难点是在进行第二次反均衡时，\(T_2(·)\)的并不是一个严格单调递增的函数，其中有多个像素值被映射为了同一个像素值。因此其反函数\(T^{-1}_2(·)\)在反映射过程中需要将这些原本混合的像素值重新分离，一般采用的方法是将它们映射为与原图更为接近的像素值。
下图展示了一个直方图匹配的例子：

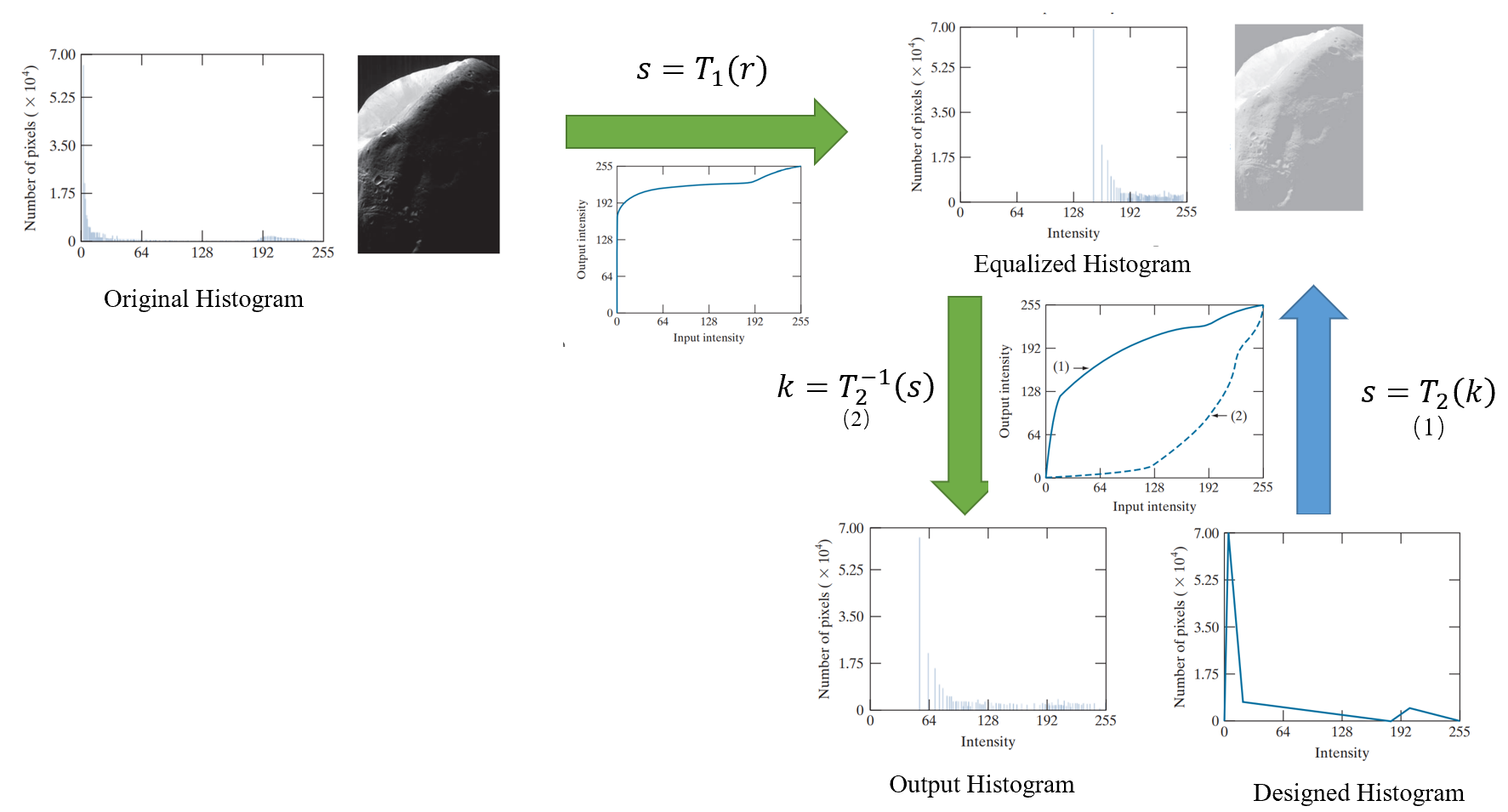
相邻处理

与点处理比较，（Neighborhood Processing）相邻处理的输入值仍然是一个像素值，但是输出值确实一个围绕输入像素值的像素集。（如下图所示）

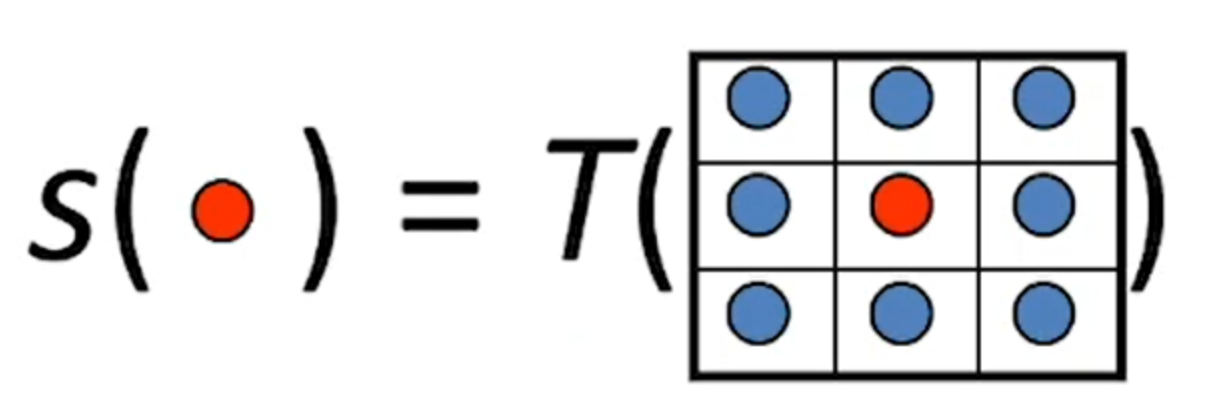
滤波（Filtering） 是一种应用于相邻处理的常见方法。
设以某个像素为中心的像素方阵称为核矩阵(Kernel/Mask matrix),以\(W\)记，核矩阵中的每一个像素值以\(w(u,v)\)表示。 将核矩阵照射至图像的某一区域\(r\)，使被照射区域中的像素值与对应的核矩阵中同位置的像素值一一相乘后全部相加，最后用一常数\(C\)调整，该过程被称为滤波。
\[s(x,y)=C∑_{(u,v)∈W}w(u,v)r(x+u,y+v)\]
整个过程可以用下图来表示：

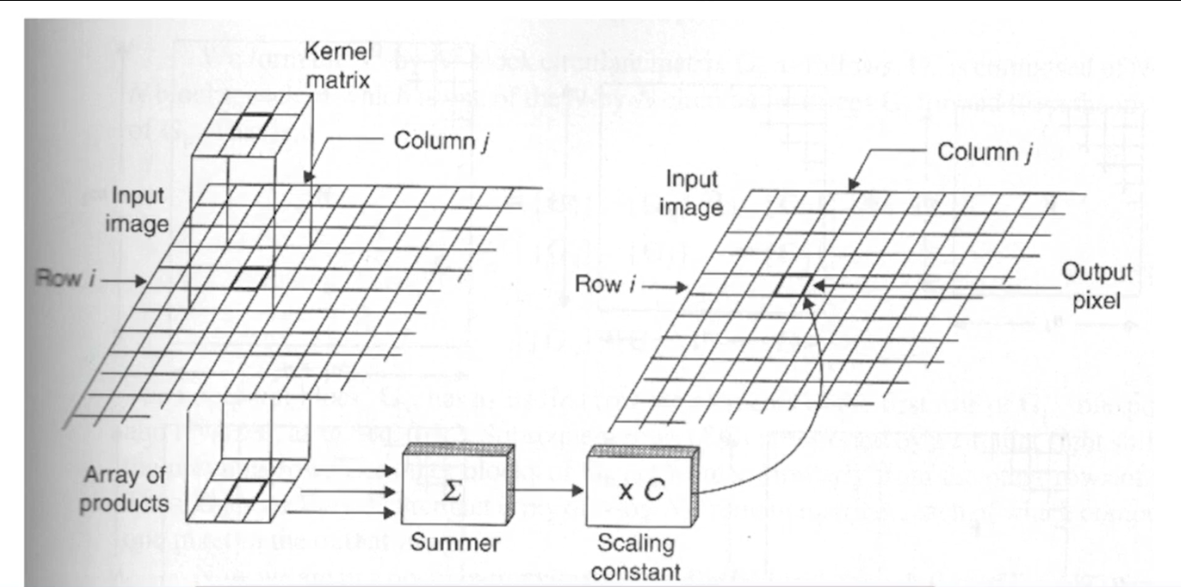
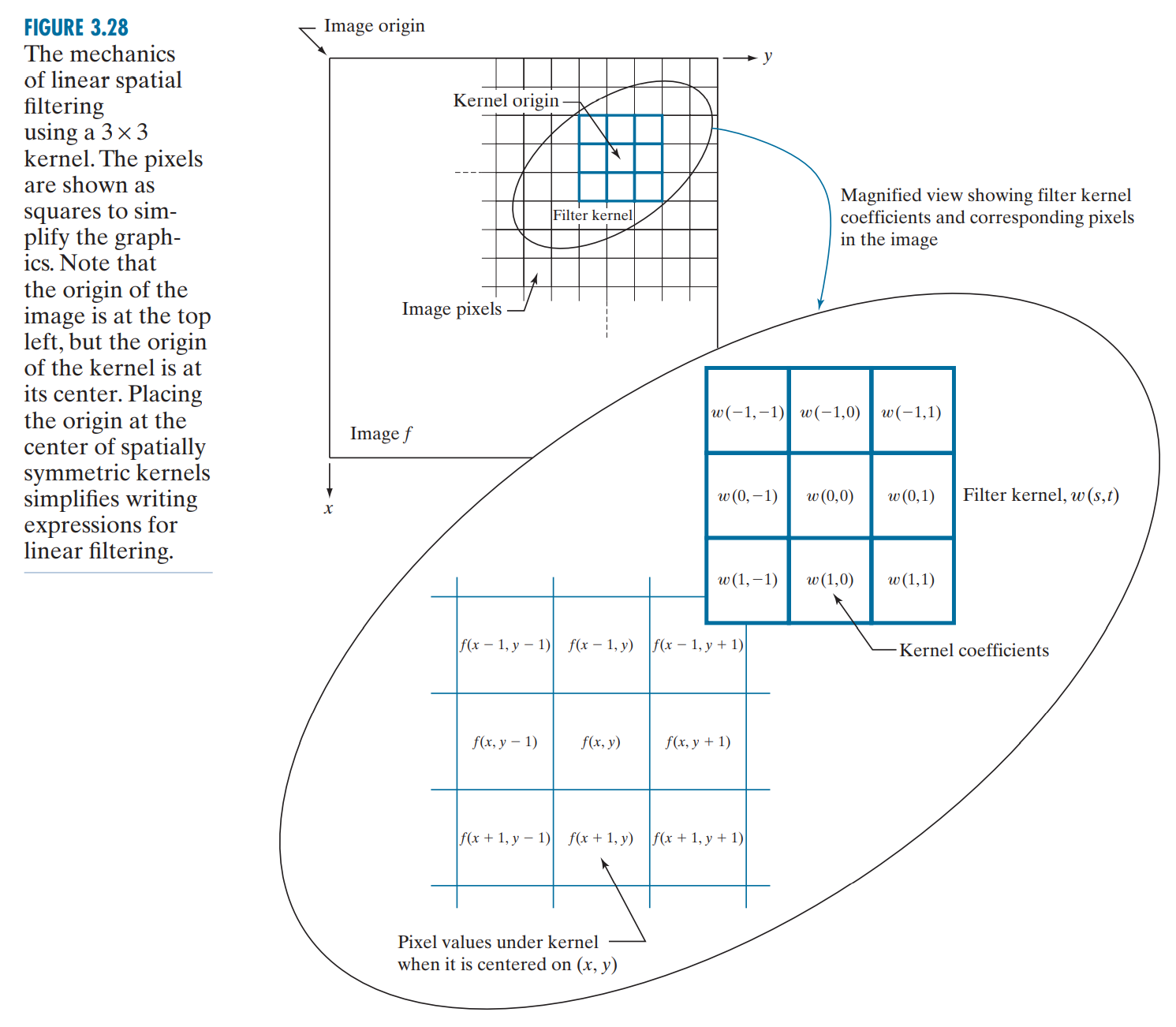
一次滤波结束后，核矩阵平移\(α\)个像素单位（称为步长(Padding)），照射图像的另一个区域，重复上述过程。

像素的邻接

需要特别说明的是，在图像处理中，像素的邻接(heighborhood)通常有4邻接(4-adjacency)和8邻接(8-adjacency)两种，如下图所示：

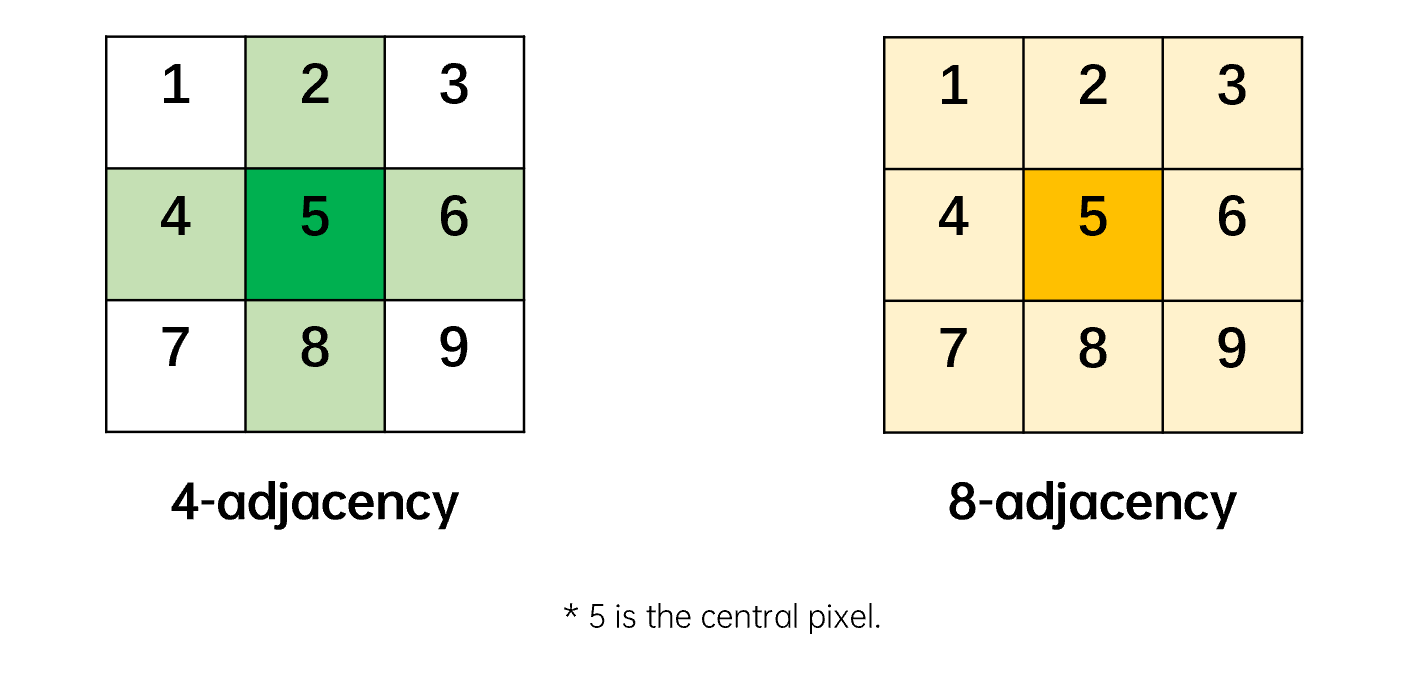
相邻处理中的邻接通常指8邻接，而下文边缘检测中的邻接通常指4邻接。

均值滤波

均值滤波的核矩阵如下：
\[\frac{1}{n}×\begin{bmatrix} 1&1&...&1\\...&...&...&...\\ 1&1&...&1 \\ 1&1&...&1\end{bmatrix}\]
其中\(n\)表示方阵元素的数量。
这样最终的输出结果是取像素点周围领域的平均值作为响应输出。在图像的边界，两个像素值差距较大的像素都被它们的平均值所代替，那么边界也不再清晰，因此最终的图像是模糊的。

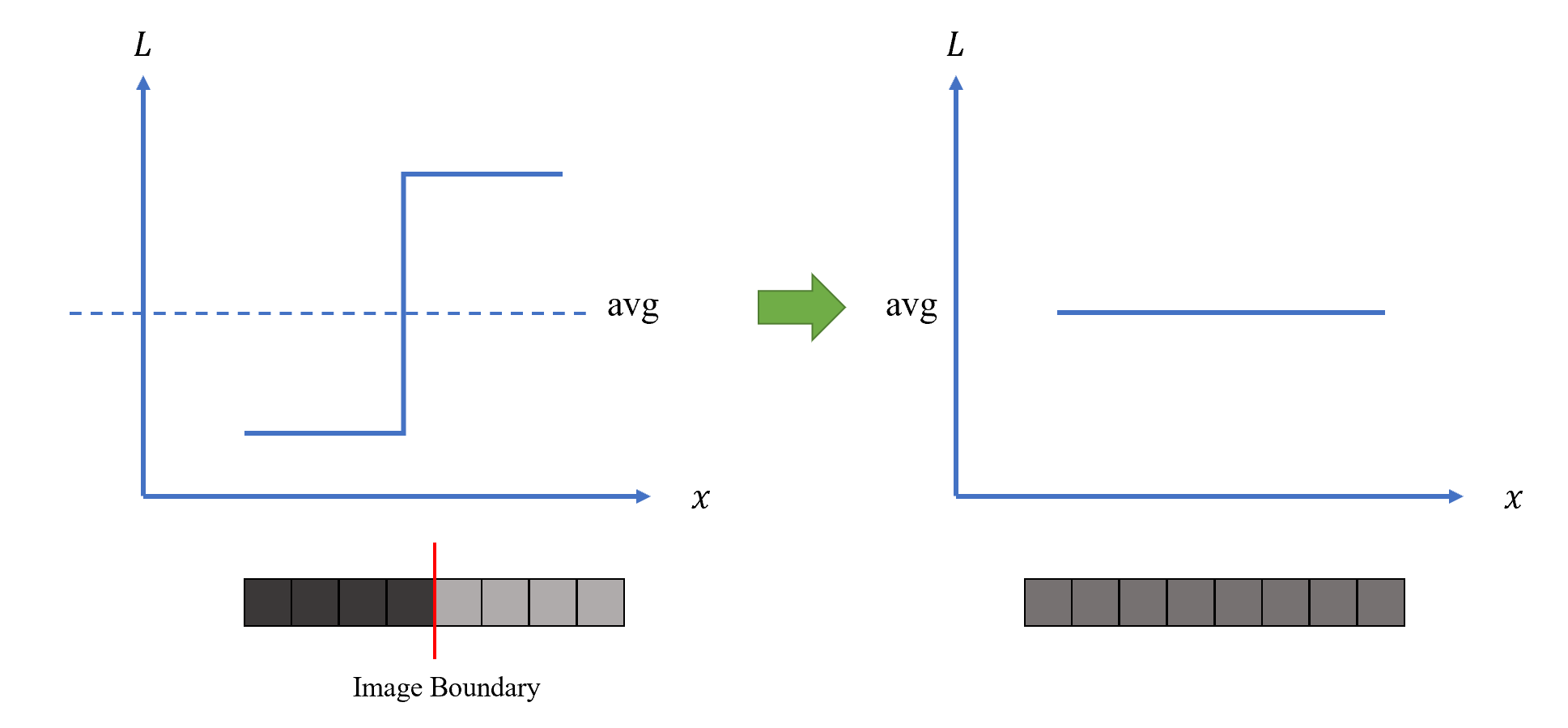
下面从数学角度分析均值滤波的合理性：对于一个核矩阵照射到的区域，倘若用一个数\(a\)替代将这个区域内的像素值，设新图与原图的均方差表示为：
\[MSE=∑_{i}(a-r_i)^2\] 其中\(r_i\)表示对应位置上的像素值。 当\(a\)为这些像素值的均值时，此时有均方差最小。

均值模糊的重要作用是将图像中的噪点通过模糊化图像的方法移除。

中值滤波

中值滤波(median filtering)的过程是将核函数照射到的区域中的像素从大到小排列，选择最中间的像素值替代所有的像素值。
中值滤波的优化目标是:
\[f(a)=∑|a-r_i|\] 当\(a\)为所有像素的中值时有优化函数最小。
椒盐噪声(salt-pepper noise)是一种将图像上的某些像素点随机地替换为另一些固定的、且较大或者较小的像素值制造的噪声。中值滤波特别适合用于处理椒盐噪声，这是因为椒盐噪声往往是由一些极大或极小的像素值组成的，在中值滤波中这些像素值一般不会被选中作为中值。

相比于均值滤波，均值滤波会有极大的可能性引入新的像素值，而中值滤波使用原图中已经存在的像素值，因此处理后的图像更接近于原图。在图像的边缘，由于中值滤波使用的是边缘本来就存在的像素，而均值滤波使用的像素大概率是新引入的均值像素，因此中值模糊的模糊程度通常要低于均值模糊。

▲上面的三张图依次是：原图（有椒盐噪声），进行均值滤波和中值滤波的输出。

下面的MATLAB程序展示了如何对图像增加椒盐噪声，并且使用中值滤波进行去除。

I = imread('test.jpg');
J = imnoise(I,'salt & pepper',0.09); % add salt and pepper noise
K = medfilt2(J); % median filter
figure(1); imshow(I);
figure(2); imshow(J);
figure(3); imshow(K);

高斯滤波

高斯滤波(Gaussian filtering)的核矩阵内的元素在三维上符合标准高斯/标准正态分布，且最高点在核矩阵中心处，如下图所示。

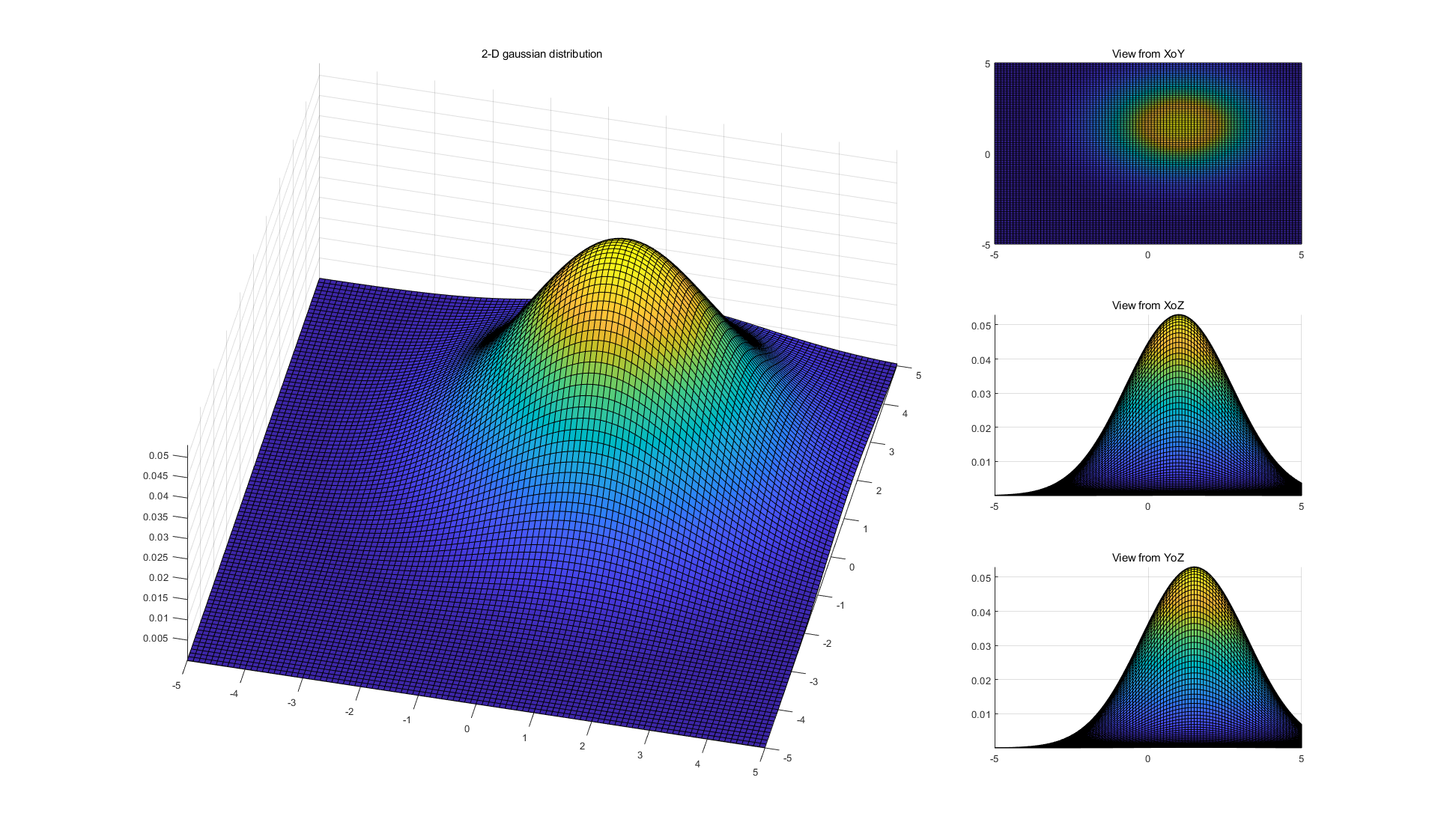
其具体的计算公式为：
\[G(x,y)=\frac{1}{2πσ^2}e^{-\frac{x^2+y^2}{2σ^2}}\]
\(σ\)是标准高斯分布中的方差，\(σ\)较小时，图像的峰值窄且高。
例如当\(σ=1.4\)时，其核矩阵可以取：
\[\frac{1}{115}\begin{bmatrix} 2&4&5&4&2\\ 4&9&12&9&4\\ 5&12&15&12&5\\ 4&9&12&9&4\\ 2&4&5&4&2\\ \end{bmatrix}\]

高斯滤波的作用是将图像模糊，使图像呈现一种毛玻璃的质感。运用高斯滤波处理图像的方法又被称为高斯模糊(Gaussian Blurring)。

高斯模糊可以移除高斯噪声。

边缘检测·图像锐化

差分的物理意义

一阶差分

数字信号的微分实则为序列的前一项与这一项的差，因此又被称为差分(differential)。
\[\frac{df}{dt}⇔f(x+1)-f(x)\] 数字图像是二维的，二维的一阶差分表示为：\(x\)方向或\(y\)方向上前一项对后一项的差，可以由下图表示：

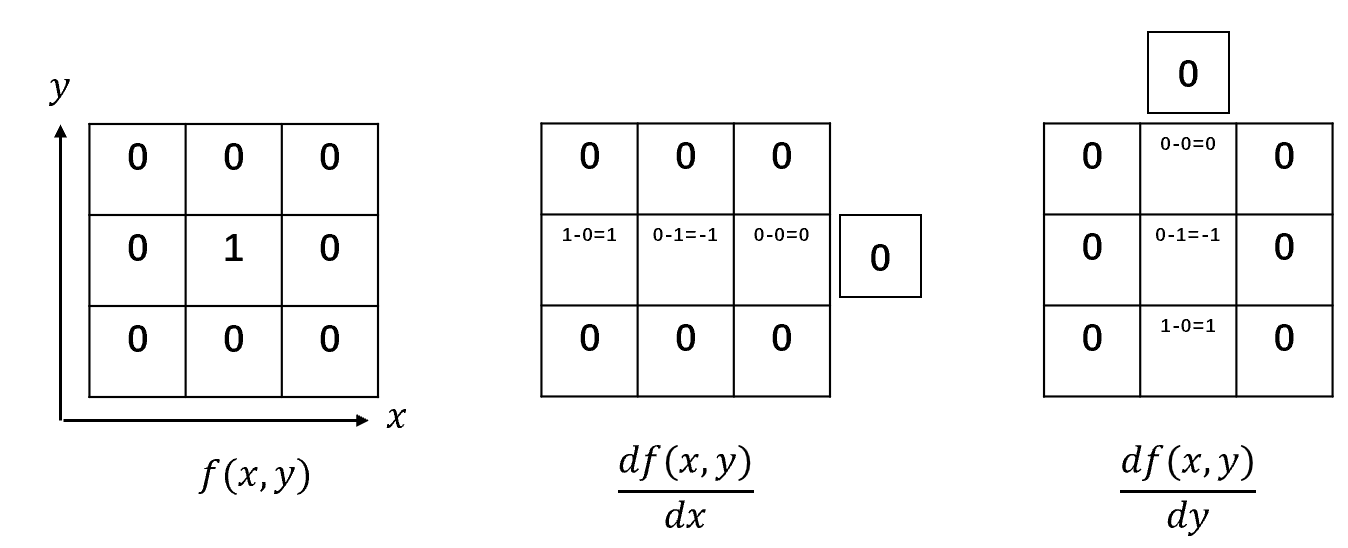
可以发现，一阶差分实际衡量了序列前一个像素值与这个像素值的相似程度：如果两个像素值完全相同，那么其差分应当为0. 换句话说，一阶差分表示了图像沿着\(x\)方向或者\(y\)方向上像素值是否发生了变化，并返回这个变化的剧烈程度。

二阶差分

二阶差分是一阶差分的差分，由如下式子给出：
\[\frac{d^2f}{dt^2}⇔[f(x+1)-f(x)]-[f(x)-f(x-1)]=f(x+1)+f(x-1)-2f(x)\]

可以由下图表示：

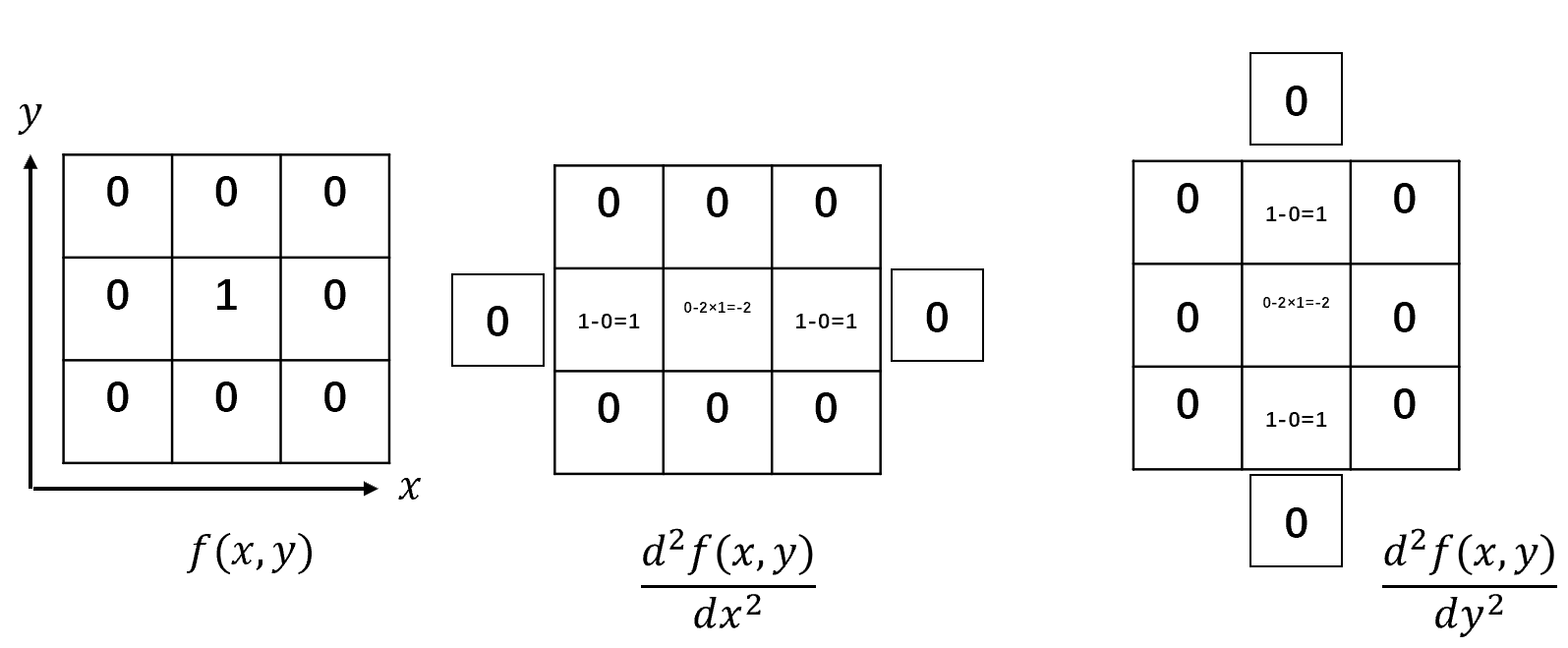
可以发现，当像素值的变化趋势发生改变时，其二阶差分不再为0。二阶差分可以发现像素值变化趋势的改变点。

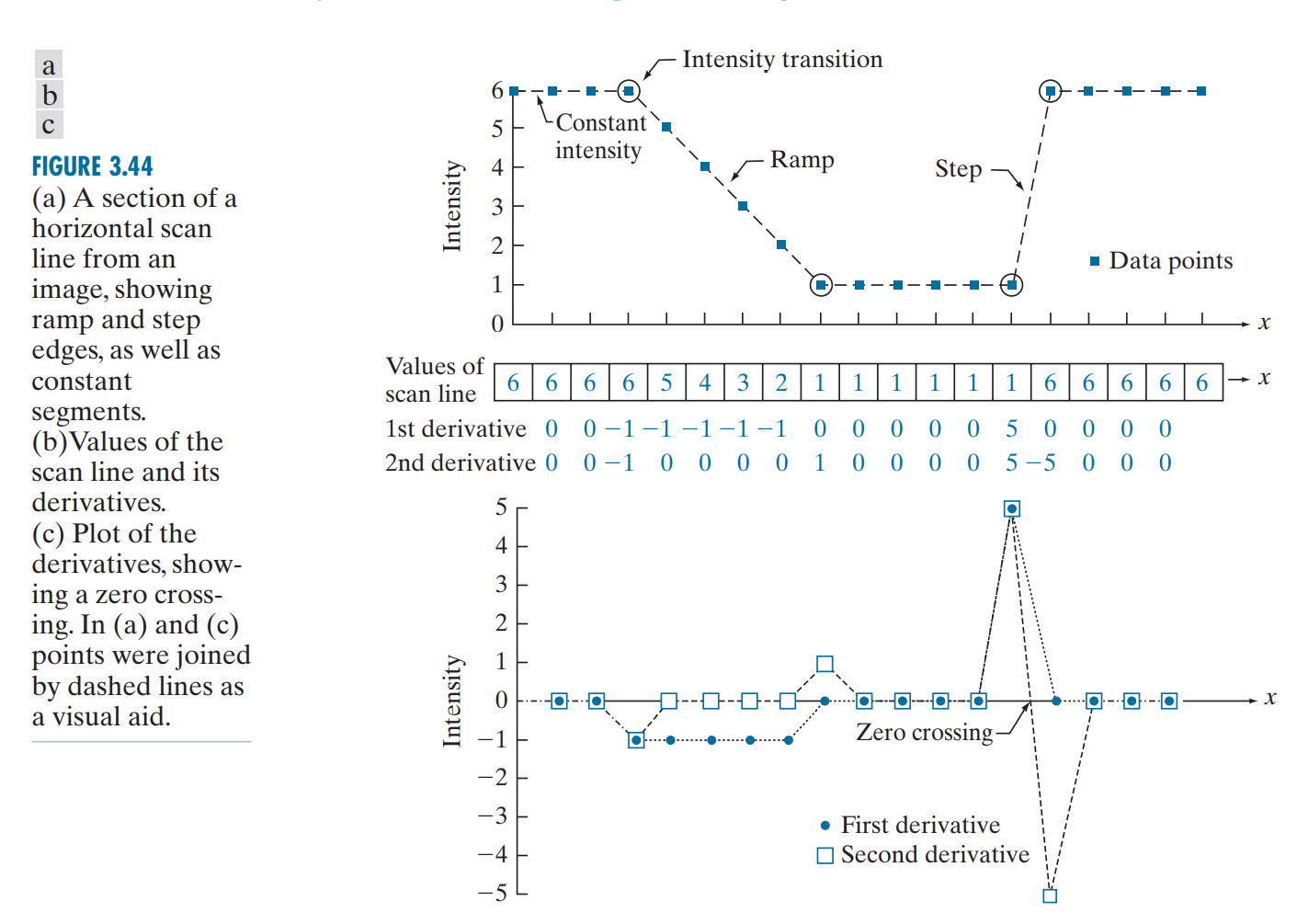
总而言之，差分可以检测图像中像素值发生变化的部分，而这些部分往往是图像中物体的边缘。因此，利用各种差分方法可以检测图像中物体的边缘，这种技术称为边缘检测(edge detection)。

拉普拉斯算子

设:
\[F=\begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0\\ \end{bmatrix}\] 定义拉普拉斯算子(Laplacian operator)为基础图像\(F\)在\(x\)方向与\(y\)方向上二阶导的和:
\[▿F=\frac{d^2F}{dx^2}+\frac{d^2F}{dy^2}=\begin{bmatrix} 0 & 0 & 0\\ 1 & -2 & 1\\ 0 & 0 & 0\\ \end{bmatrix}+\begin{bmatrix} 0 & 1 & 0\\ 0 & -2 & 0\\ 0 & 1 & 0\\ \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\]

图像与这个算子发生卷积后\(I\*▿F\)，就能够提取出图像的边缘。
此外还有一些拉普拉斯算子的变体，这些变体可以使得图像边缘更易于提取:
\[\begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\begin{bmatrix} 0 & -1 & 0\\ -1 & 4 & -1\\ 0 & -1 & 0\\ \end{bmatrix}\begin{bmatrix} 1 & 1 & 1\\ 1 & -8 & 1\\ 1 & 1 & 1\\ \end{bmatrix}\begin{bmatrix} -1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1\\ \end{bmatrix}\]

下图展示了一个使用边缘检测算子的例子，将提取的边缘与原图进行叠加后，原图像中的由边缘检测算子提取到的图像细节被加强，称为图像锐化(sharpened)。

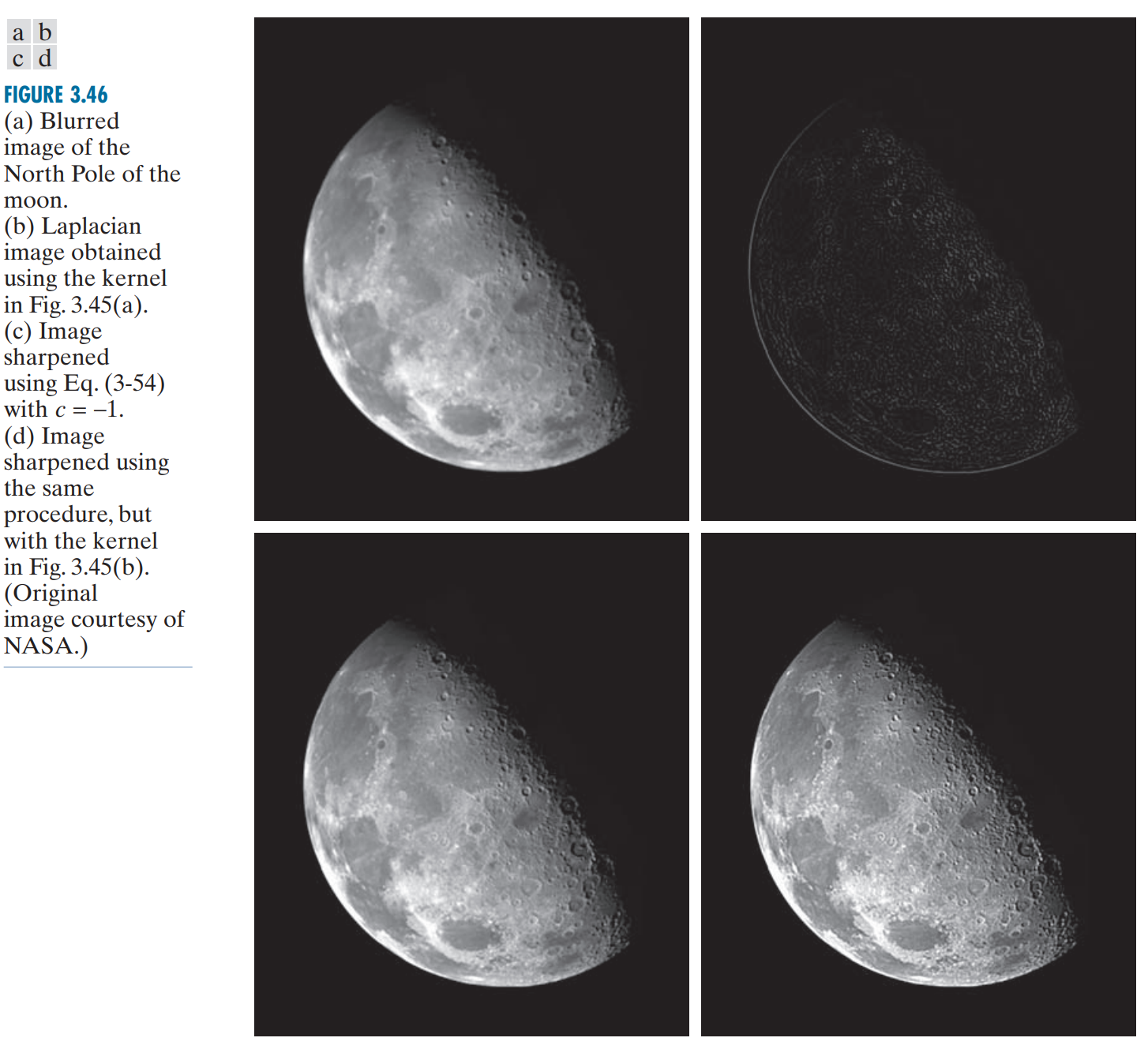
反锐化遮罩

反锐化遮罩(unsharp marking, USM)算法是另一种边缘提取的方法。反锐化遮罩的基本思想是：由于模糊算法（均值滤波、中值滤波等）会特别地将图像像素变化剧烈的物体边界部分进行模糊处理，那么倘若将模糊后的图像与原图像进行差分，那么差分的结果将会是这些被模糊的边界部分，以此提取出图像中物体的边缘。

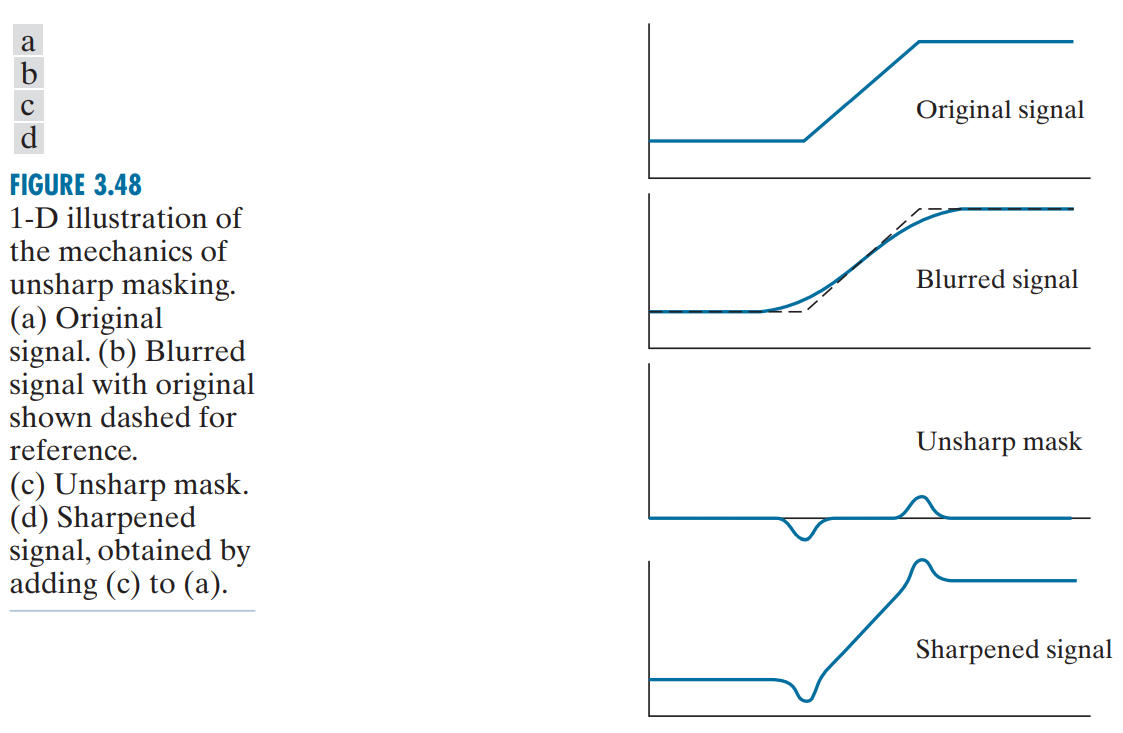
同样地，将提取到的边缘与原图进行叠加，原图中的边缘将被锐化。

下面的MATLAB程序展示了如何利用中值滤波实现反锐化遮罩。

I = imread('test.jpg');
K = medfilt2(I); % smooth out img (by using median flt)
figure(1); imshow(I);
figure(2); imshow(I-K); % edges of img
figure(3); imshow((I-K)*2+I); % sharpened img