07.图像复原

本文最后更新于 2024年1月27日下午

图像复原

成像过程中的“退化”(degrade)现象主要指成像系统受到各种因素的影响，诸如成像系统的散焦、设备与物体间存在相对运动或者是器材的固有缺陷等，导致图像的质量不能够达到理想要求。此外退化的图像中还会有各种噪声。如何将一张退化的图像进行复原，这是图像复原(image restoration)的主要任务。

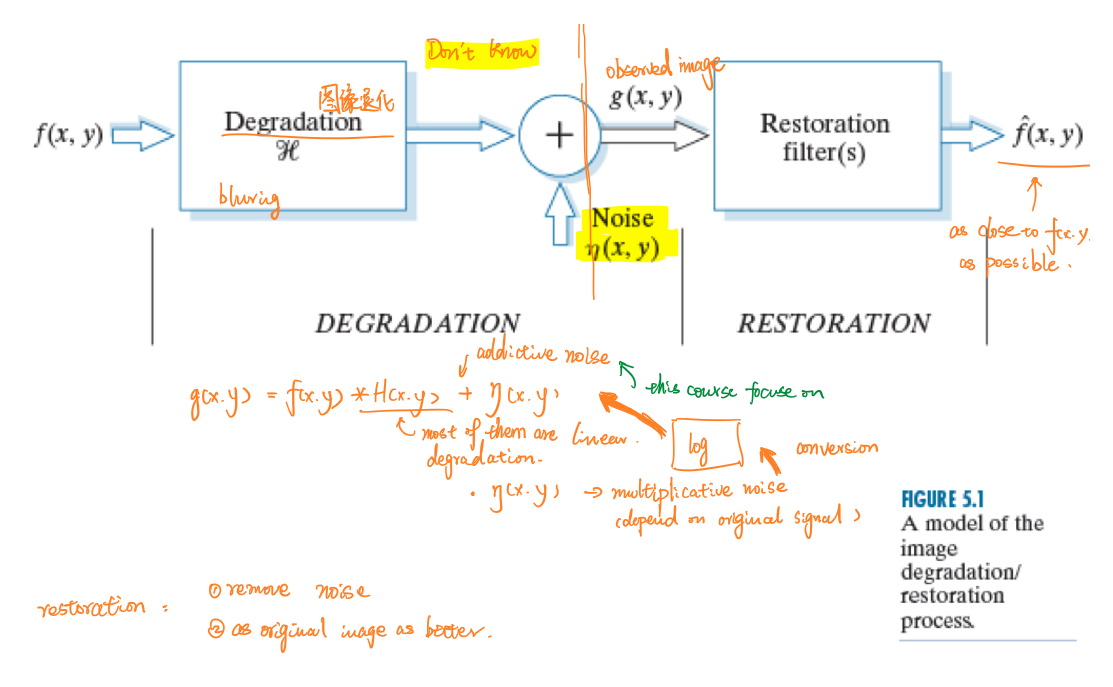
整个过程用数学公式表示为：
\[g(x,y)=f(x,y)*\mathcal{h}(x,y)⊙η(x,y)\] 其中\(\mathcal{h}\)是使得图像退化的过程；\(η(x,y)\)是噪声；\(⊙\)在噪声为加性噪声时为\(+\)，在噪声为乘性噪声时为\(×\)。
和退化过程正好相反，复原的过程首先会去除图像原本的噪声，再对退化进行恢复。
图像复原的过程类似于图像增强，和图像增强不同的是：图像复原的目的是为了尽可能地使图像接近原始图像，而并非将凸显图像中某些特定信息。

噪声及其复原

噪声可以分为两类：加性噪声(additive noise)和乘性噪声(multiplitive noise)。加性噪声附加在原始信号后，其强度与原始信号无关，而乘性噪声与原始信号相乘，其强度与原始信号有关。本节中主要研究加性噪声。实际研究中可以采用取对数的方式将乘性噪声转变为加性噪声。

常见噪声类型

人们常常依据噪声所遵循的分布来为噪声分类。

高斯噪声

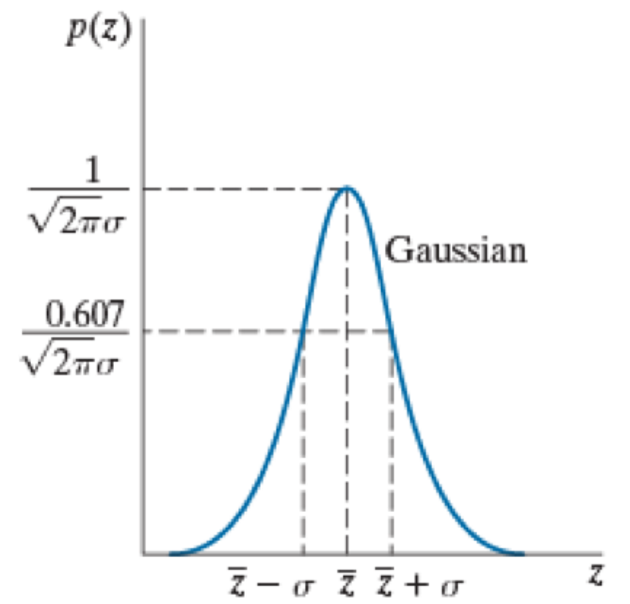
高斯噪声(Gaussian noise)是最基础的一种噪声，也被称为白噪声。高斯噪声的概率密度函数可以表示为：
\[p(z)=\frac{1}{σ\sqrt{2π}}exp(-\frac{(z-μ)^2}{2σ^2})\] 其中\(μ\)是均值，\(σ\)是方差。
需要注意的是，高斯噪声在现实世界是不存在的，没有一种真实的系统可以制造高斯噪声，但是高斯噪声仍然具有很高的研究价值。其原因一是在数学上高斯噪声比较容易处理，其二是其他的真实噪声的某些部分往往较为贴近高斯噪声的分布。

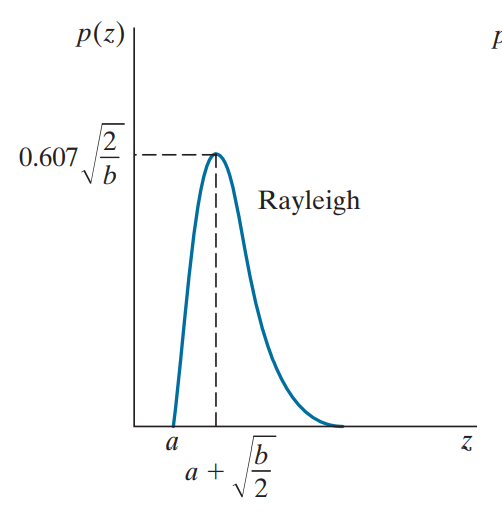
瑞利噪声

瑞利噪声(Rayleigh noise)是一种真实存在的噪声，它主要存在于核磁共振图像和水下摄影图像中，其概率密度分布不对称。
其概率密度函数为：
\[p(z)=\begin{cases} \frac{2}{b}(z-a)exp(-\frac{(z-a)^2}{b}),z ≥a\\ 0,z<a \end{cases}\]

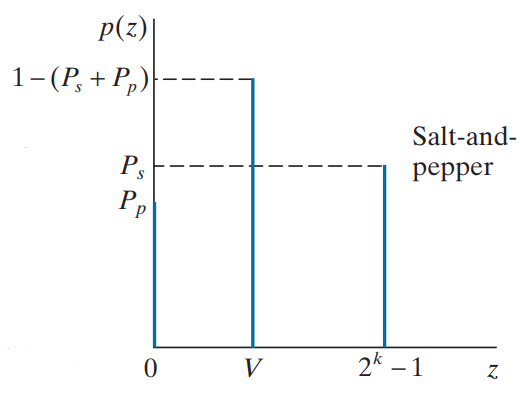
椒盐噪声

椒盐噪声(salt and pepper noise)也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。
椒盐噪声会随机地将某些特定的像素值改变为另外一些像素值，其概率密度公式表示为：
\[p(z)=\begin{cases}p_p,z=0\\1-p_s-p_p,0<z<L\\p_s,z=L\end{cases}\]

此外还有其他的常见噪声，比如伽马噪声和指数噪声，它们的概率分布及统计特性已经在课程《可靠性工程》中有过介绍，故在此省略。

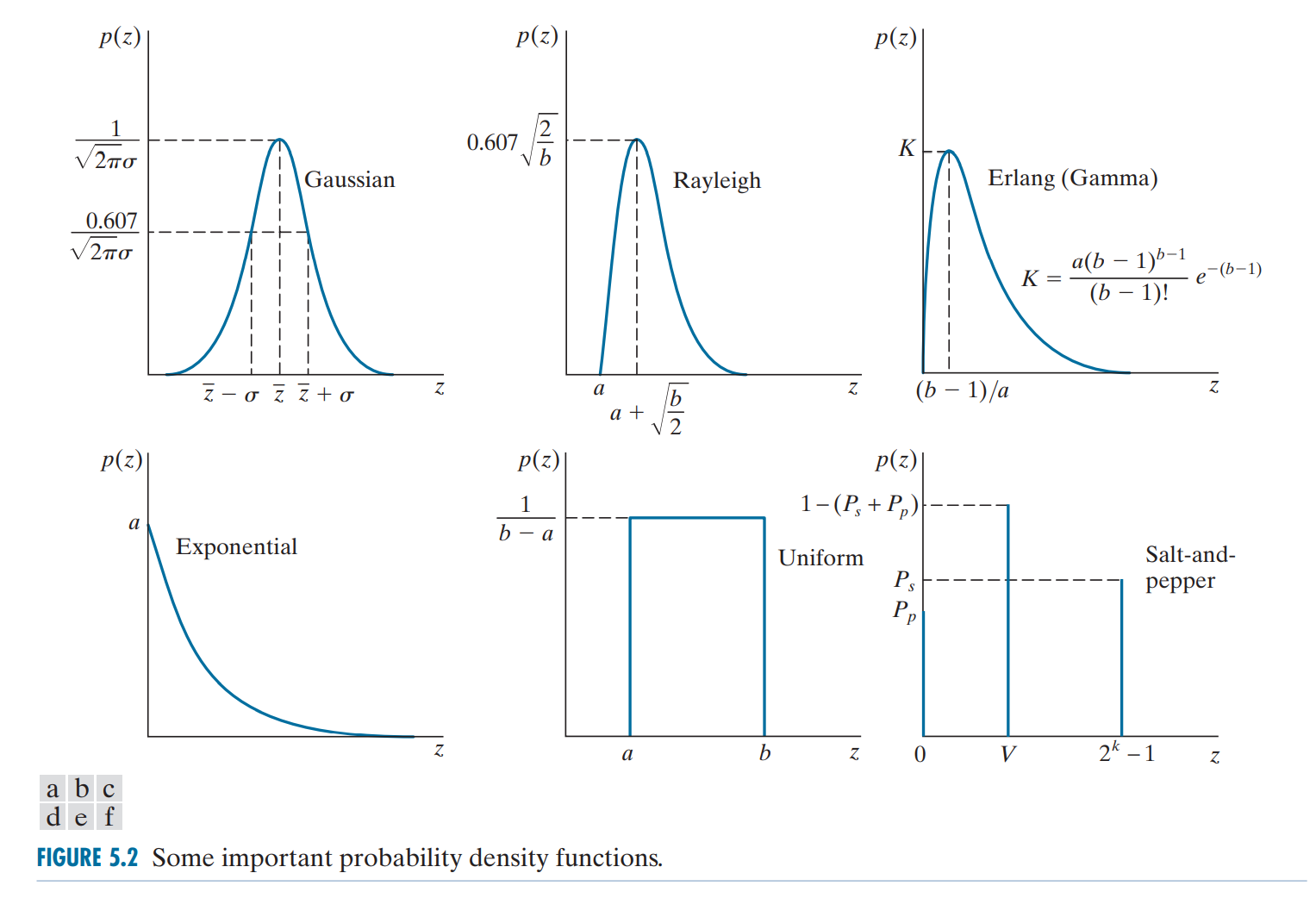
噪声估计

下面来研究不同类型的噪声对图像的影响，下图显示了六种噪声（高斯噪声、瑞利噪声、伽马噪声、指数噪声、均匀噪声、椒盐噪声）对于同一张只包含三个像素值的图像在亮度直方图上的影响。

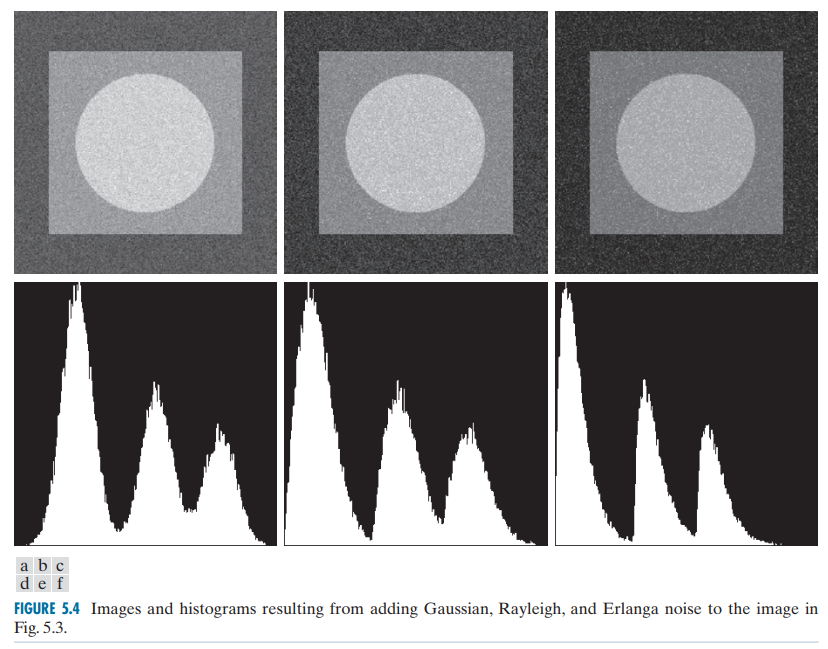
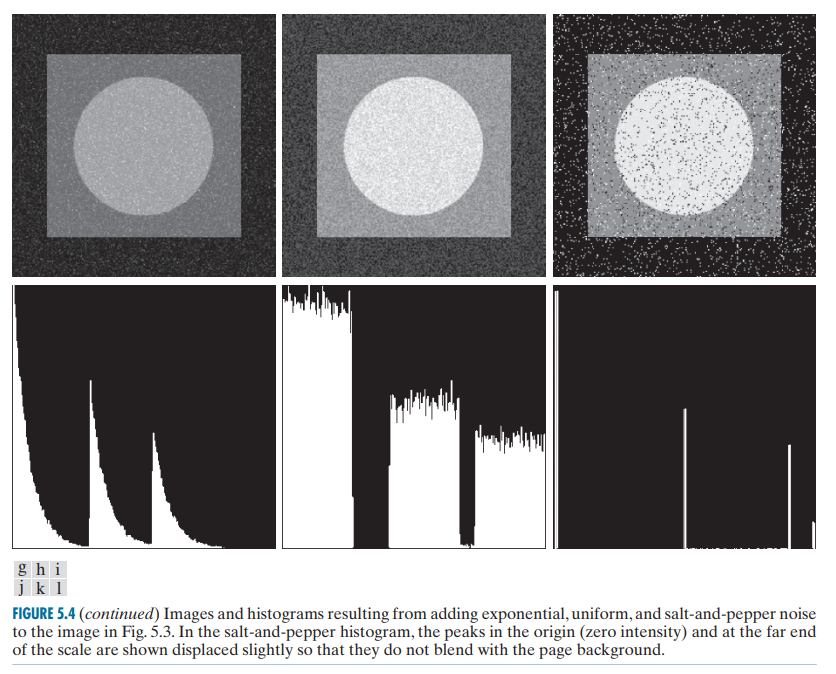
观察上图可以发现，原图直方图的每一个冲激被延拓为以其为统计中心对应的噪声包络。可以总结：噪声对图像的的影响是将图像上每个像素对应的分布延拓到相邻的像素值，这个延拓的包络形状为该噪声概率密度分布函数。
因此，通过观察图像对应直方图上像素值的包络可以判断出图像噪声的类型。

实际的图像包含的色彩/灰度相较于上面的例子中的原图更多，这种情况下，通常是截取图像中看起来颜色均匀的一部分，再通过分析其直方图的包络形状估计图像的噪声类型。

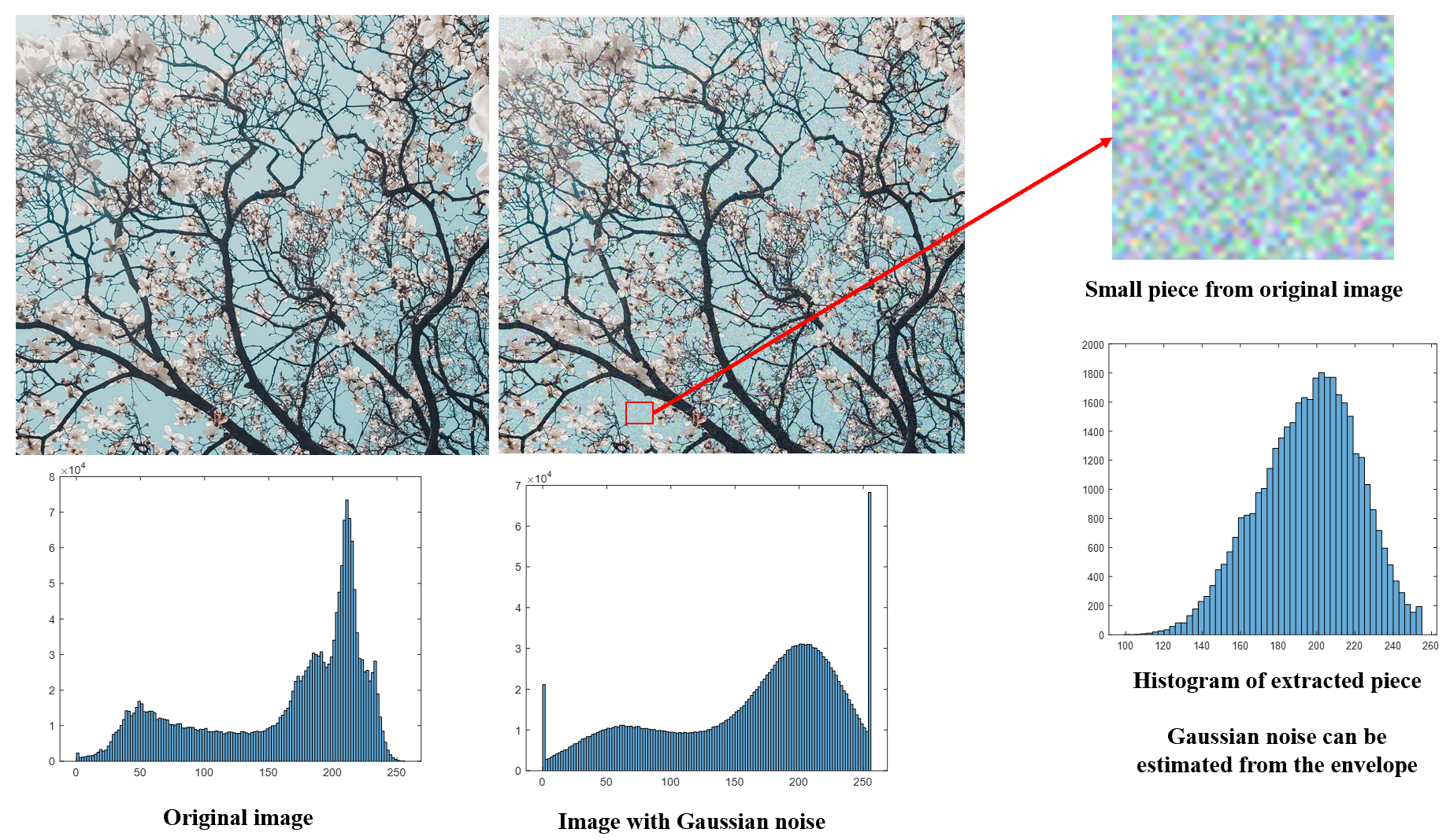
有一些噪声的概率分布函数较为近似，比如瑞利噪声和高斯噪声，这种情况下则使用两种概率模型对直方图的包络线进行拟合，再比较两者拟合结果的均方差，选择均方差较低的拟合方案。

噪声去除

噪声估计的目的是为了根据图像的噪声类型选择合适的滤波器以及滤波器合适的参数去除噪声（比如：高斯噪声-高斯滤波器，椒盐噪声-中值滤波器）。
因此整个噪声去除的流程为：
1. 估计噪声 2. 根据噪声选择合适的滤波器和滤波器类型 3. 噪声过滤

如果去除噪声后的照片\(\hat{f}(x,y)\)和原图（原图只添加了噪声）的差距仍然很大，那么可能的原因有两点：
- 噪声估计过程中错误地估计的噪声的类型和噪声参数。
- 使用了错误的滤波方法。

退化及其复原

常见退化方式

高斯模糊

高斯模糊即高斯滤波。虽然高斯模糊不存在于真实世界，但是许多真实的模糊可以被近似地看做高斯模糊进行处理。

运动模糊

运动模糊(motion blurring)是由于在相机曝光时间中被摄物体与相机发生相对运动而造成的模糊。运动模糊可以理解为多张被摄物体照片在曝光时间\(T\)上的时域叠加，每张被叠加的照片上被摄物体都有一小段位移。

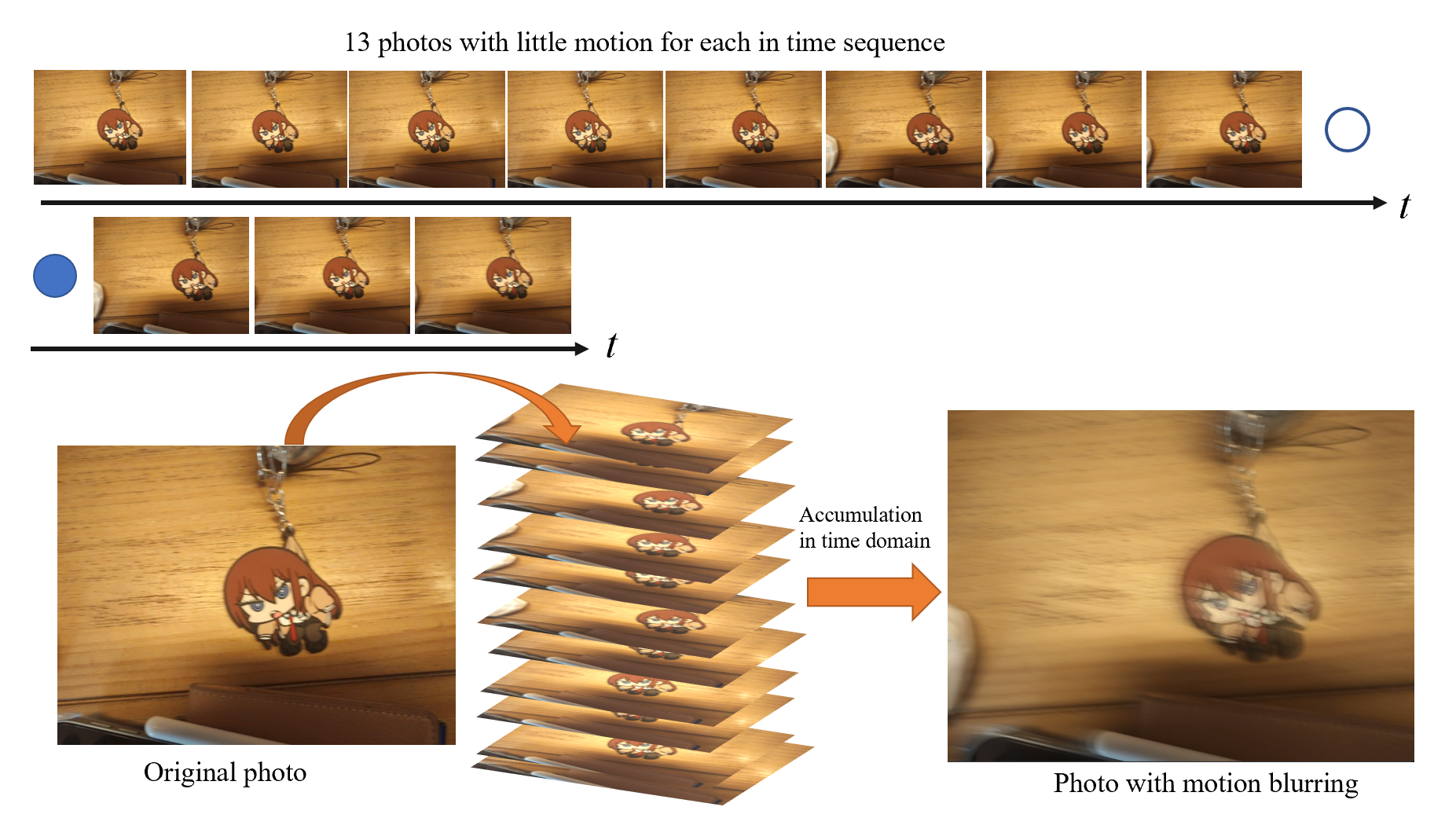
运动模糊后的照片\(g(x,y)\)可以用数学表示为：
\[g(x,y)=∫_0^Tf(x-x(t),y-y(t))dt\]

逆滤波

复原退化的其中一种方法是逆滤波(inverse filtering)。它的基本思路如下：
经过除噪后的图像可以表示为：
\[g(x,y)=f(x,y)*\mathcal{h}(x,y)\] 在频域中，卷积将变为乘法，更易于处理，因此对等式两边同时使用傅里叶变换：
\[G(u,v)=F(u,v)\mathcal{H}(u,v)\] 那么原图的频域表示为：
\[F(u,v)=\frac{G(u,v)}{\mathcal{H}(u,v)}\] 因此，倘若能够正确估计退化函数\(\mathcal{H}(u,v)\)或者\(h(x,y)\)，那么图像就可以通过与退化函数相除，再进行傅里叶反变换被正确复原。
逆滤波的难点是如何估计退化函数\(\mathcal{H}\)，通常情况是根据经验预测图像所经受的退化类型，但是也有可能原始图像本身就是一张退化图像，这种情况下退化函数难以被估计。

维纳滤波

维纳滤波(Wiener filtering)是另一种复原退化的方法。其基本思想是将原图和复原图的均方差表达式最小化，并求出此时复原图像的值。
原图和复原图的均方差表示为：
\[MSE=E[(\hat{f}-f)^2]\] 根据期望的式子将其展开，并使用傅里叶变换转到频域，最后求导，得到\(MSE\)在频域上最小的复原图表达式为：
\[\hat{F}(u,v)=G(u,v)\frac{\mathcal{H}^*(u,v)}{\mathcal{H}^2(u,v)+\frac{P_η}{P_f}}\] 其中\(\mathcal{H}^*(u,v)\)是\(\mathcal{H}(u,v)\)的共轭函数；\(P_η\)和\(P_f\)分别对应噪声\(η\)和原图\(f\)的功率谱密度，可以由维纳-辛钦定理计算得到。不过实际处理问题时由于\(\frac{P_η}{P_f}\)是一个常数，简记为\(K\)，通常不会计算这两者的功率谱密度，而是尝试如下式子：
\[\hat{F}(u,v)=G(u,v)\frac{\mathcal{H}^*(u,v)}{\mathcal{H}^2(u,v)+K}\] \[\hat{f}(x,y)=F^{-1}[\hat{F}(u,v)]\] 为\(K\)设置一个范围，然后不断地尝试不同的\(K\)值，观察\(\hat{f}(x,y)\)的清晰程度来复原图片。
下图展示了使用逆滤波法(下图第二列左图)和维纳滤波（下图第二列右图）分别复原的具有高斯模糊的图像：