1. 模拟信号和数字信号·数制[英]
本文最后更新于 2025年9月1日 上午
Types of signals and number system
Two fundamental types of signals
Analogue data(模拟/模拟信号)
- Continuous system(连续的)
- Infinite(Computer cannot process directly)
- the output of a function of the parameter being measured
Examples
temperature, sound wave
Conventional telephone: direct connection(analogue)
Digital data(数字/数字信号)
- Discrete system(不连续的)
- Finite
- Can only change by fixed units
Notice: A discrete signal maybe not finite.
Examples
number of stages, radio signal, control signal.
Mobile phone:End to end/indirect connection radio signal(digital)
Numerical Systems
Decimal(十进制)
- for human:readable
- symbol set:
\[\{0,1,2,3,4,5,6,7,8,9\}\] - presentation:
\[(digital part)_{(decimal)}\] like: \(25_{10}\) \[d_nd_{n-1}...d_2d_1d_0d_{-1}d_{-2}...d_{-n+1}d_{-n}\] Value:
\[\begin{aligned} N_{10}&=d_{n-1}×10^{n-1}+d_{n-2}×10^{n-2}+...+d_1×10^1+d_0×10^0+d_{-1}×10^{-1}+...+d_{-m}×10^{-m}\\ &=∑_{i=-m}^{n-1}d_i×10^i \end{aligned}\]
Binary(二进制)
- for machine:high execution efficiency but a smell number in Decimal can be a large number in Binary.
- symbol set:
\[\{0,1\}\] - presentation:
\[b_nb_{n-1}...b_2b_1b_0b_{-1}b_{-2}...b_{-n+1}b_{-n}\] Value:
\[\begin{aligned} N_{2}&=b_{n-1}×2^{n-1}+b_{n-2}×2^{n-2}+...+b_1×2^1+b_0×2^0+b_{-1}×2^{-1}+...+b_{-m}×2^{-m}\\ &=∑_{i=-m}^{n-1}b_i×2^i \end{aligned}\]
X-based
- symbol set:
\[\{0,1,...,X\}\] - presentation:
\[b_nb_{n-1}...b_2b_1b_0b_{-1}b_{-2}...b_{-n+1}b_{-n}\] Value:
\[\begin{aligned} N_{X}&=x_{n-1}×X^{n-1}+x_{n-2}×X^{n-2}+...+x_1×X^1+x_0×X^0+x_{-1}×X^{-1}+...+x_{-m}×X^{-m}\\ &=∑_{i=-m}^{n-1}x_i×X^i \end{aligned}\]
Conversion between different numerical systems
Decimal to binary
Integer
Successive division(短除法/大除法)
Dividing number by 2 and remove the integer part until the integer part is 0, and put the remainder of each step in inverse calculation order.
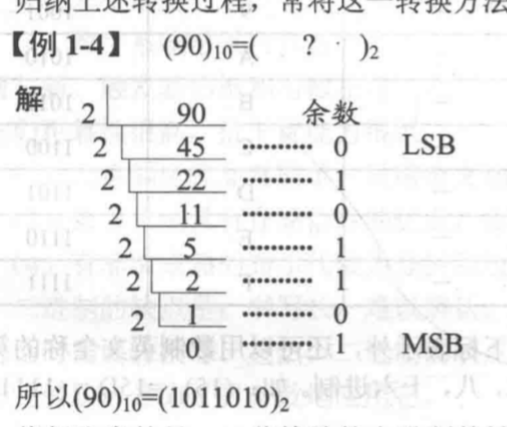
Float
Integer part to Binary and float part to Bin and add them up.
Example: \(3.0125→3+2^{-3}→11+0.0012→11.0012\)
Negative
- one’s complement(反码/1补码)
0 is converted to 1 and 1 is converted to 0.
- two’s complement(补码/2补码)
one’s complement +1.
Example: \(5_{10}=101_2=0101_2 \text{(防止溢出)}→one's complement→1010_2→two's complement→-510=1011_2\)
Conclusion
Add a “0” in initial and do one’s and two’s complement.
We always add a place before the number to represent whether the number is positive or not. (符号位)
And 1 present for negative 0 present for positive.
Example: -5 in memory is 10001011 and 5 is 00001011.
Binary to decimal
Integer
The same as mentioned above.
Float
Successive multiplication: multiply by 2 and remove the integer part until the float part is 0.
Decimal to any based number
Integer
Dividing the number by n and remove the integer part until the integer part is 0, and put the remainder of each step.
Float part
Multiply by n and remove the integer part until the float part is 0.