2. 码型[英]

Type of Code

Binary-Coded Decimal (BCD)

A digit is replaced by four bits:
\[D=b_3b_2b_1b_0\]
One of \(b\) is called one bit and each bit's value has two condition: 1 or 0.

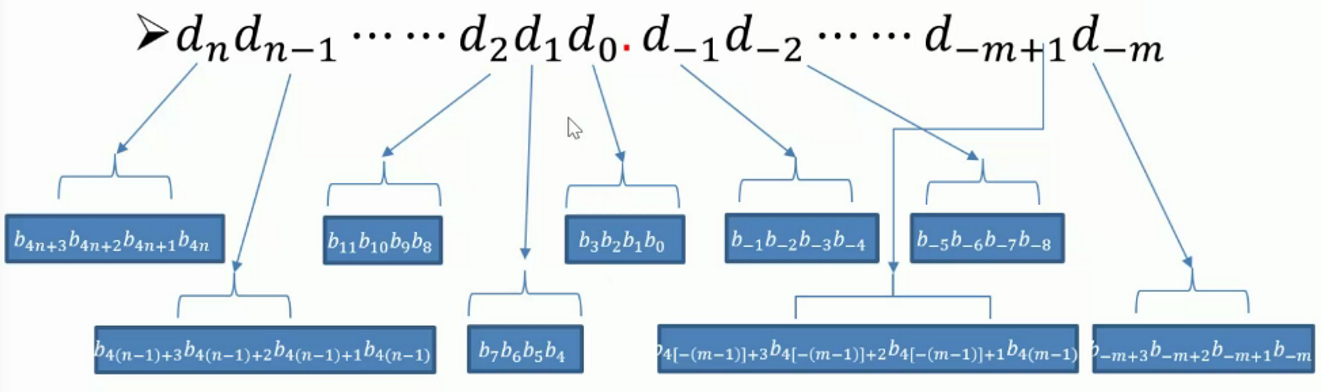
Conversion

• Dec to BCD
  Put each position to be Bin and put together.
  Examples:
  \(D=87\),\(d_1=8=1000_2\),\(d_0=7=0111_2→10000111_{BCD}\)
  \(D=34\),\(d_1=3=0011_2\),\(d_0=4=0100_2→00110100_{BCD}\)
  \(D=198\),\(d_2=1=0001_2\),\(d_1=9=1001_2\),\(d_0=1000_2\)\(→000110011000_{BCD}\)

• BCD to Dec
  Divide by very 4 bits to a integer of Dec and put together.
  Example:
  \(01010111_{BCD}\),\(0101→5\),\(1101→7\)\(→57_{10}\).

Weighted BCD(有权BCD码)

The weight（权) of each bits is different.(数位上的权发生改变，十进制数对应改变).

Example: When \(b_3b_2b_1b_0 = 1010\) ：

Weight of 4 bits		Dec
8 4 2 1	1x8+0x4+1x2+0x1	10
2 4 2 1	1x2+0x4+1x2+0x1	4
7 4 -2 -1	1x7+0x4+1x-2+0x-1	5

Common weight combinations of 4 bits are: 8421 2421 5421.

• MSB/LSB
  Most/Least significant bit (最高/最低有效位) the damage when change wrong MSB is the largest MSB is the first 1 bits and LSB is the last 1 bits.
  The common BCD is presented for 8421code and 8421code can be seen as a special condition of weighted BCD. 8421 code is the most classical one and it is also called Pure Binary Position Coding（自然二进制编码）.

Conversion

Example: \(759_{10}\):
- 8421 code
\(7=0\times8+1\times4+1\times2+1\times1\), \(5=0\times8+1\times4+0\times2+1\times1\), \(9=1\times8+0\times4+0\times2+1\times1\)
\(759_{10}=0111 0101 1001_{8421}\)

• 7421 code
  \(7=1\times7+0\times4+0\times2+0\times1\),\(5=0\times7+1\times4+0\times2+1\times1\),\(9=1\times7+0\times4+1\times2+0\times1\).
  \(759_{10}=1000 0101 1010_{7421}\)

Gray Code

Issue of Pure Binary Position Encoding

In Pure Binary Position Coding:
Black blocks stands for value is 1.
White block stands for value is 0.

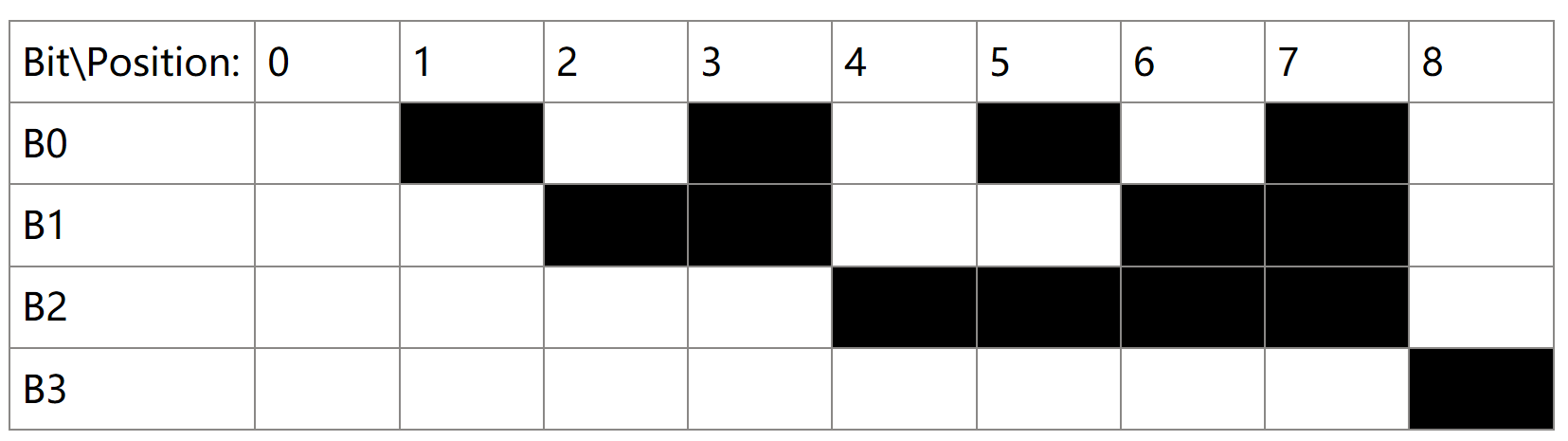
From position 1 changes to 2 , \(b_0\),\(b_1\) had changed.
But we can't decide the order of change position if the change is not simultaneous.
So during the change there could be other positions produced, which may cause danger and error.

Gray Code: Encoding Method

To prevent this potential danger, the Gray Code was invented. Gray Code has no weight.

Quick Convertion

If \(b_{n+1}\) is not existed, you can create it and let it be 0.
\[g_n=b_n⊕b_{n+1}\]

⊕/XOR/exclusive or(异或)：
a⊕b：
- if a=b, the result is 0.
- if a≠b, the result is 1.

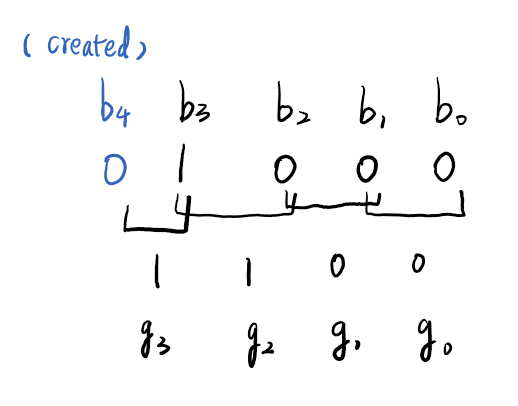
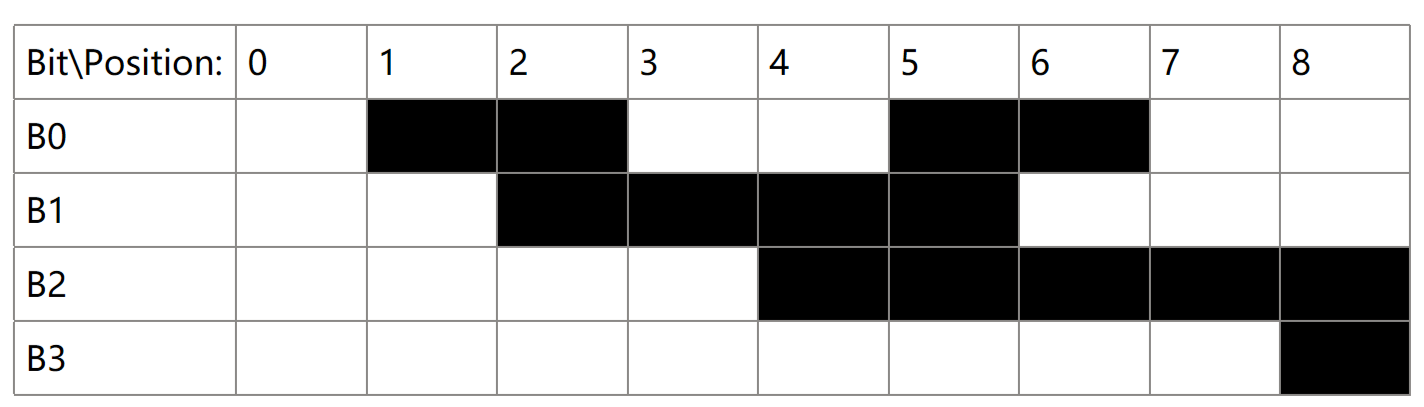
Now, from one position to another position, each change changes only 1 bit, which prevent from error and danger.

Error Check and Error Correction

When the value of some positions changed during the transition, error happens.

Below shows how a sender and receiver detect a single position error:
- Sender
1. Calculation on the number of 1 2. Generate a parity code - Receiver
1. Calculation on the number of 1 2. Generate a new parity code 3. Compare

Parity Code （奇偶校验码）

Parity code is added to make the number of "1" in data segment always is an odd/even.

Parity Block Checks

For \(b_3b_2b_1b_0\) we calculate every 3 bits for a parity code 3 times and evaluate to \(P_1P_2P_3\).
The data package will be send like \(\underline{P_1b_3b_2b_1}\) , \(\underline{P_2b_3b_1b_0}\) , \(\underline{P_3b_2b_1b_0}\).
When receiving the data, we do the calculation again and check with \(P_n\).
If error happens, we can locate the error and correct.

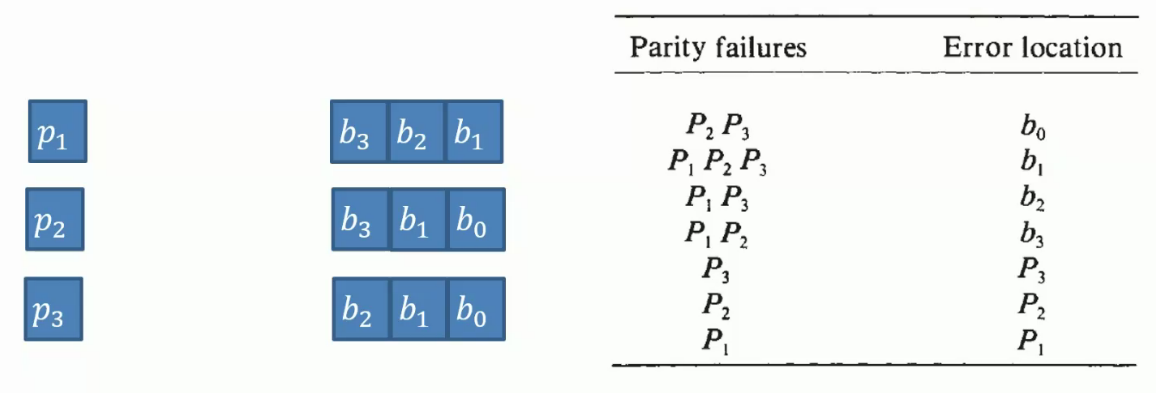
Also we can do the calculation of total to generate a parity block to make the number of 1 all bits n is odd/even.

Example:

M-in-N/M-out-of-N/M-of-N Code(m中取n码)

N stands for total number bits.
M stands for m bits must be set to 1.
If the number of 1 in a data package is not equal to m, error happens.

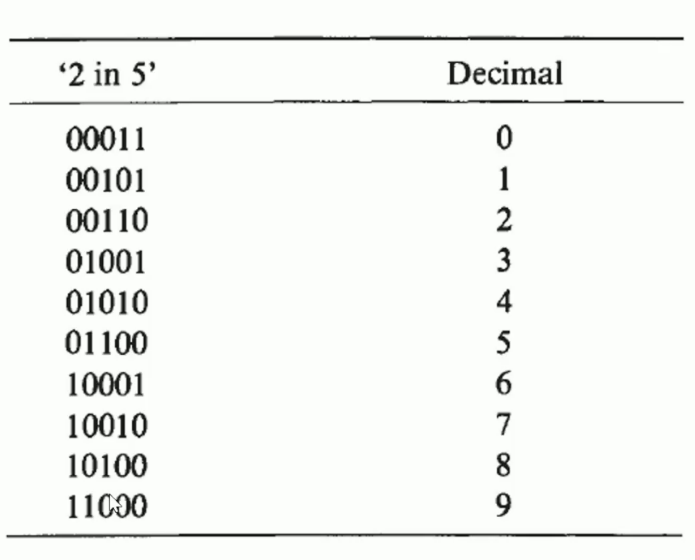
Common case is 2 in 5 code or 3 in 5 code.

Example: Bar Code is a kind of m-of-n code.