应用随机过程
本文最后更新于 2025年6月4日 晚上
应用随机过程——期末复习笔记
[参考教材]:刘次华.随机过程(第五版)[M].武汉:华中科技大学出版社,2014
考试形式:八道大题,5道简单题(每题10分),2道解答题(每题20分),1道证明题(10分,证明题一般为证明平稳过程)
预备知识
特征函数
\[ g(t)=E[e^{itx}]=\int_{-\infty}^{+\infty} e^{itx}dF(x) \]
离散型 \[ g(t)=\sum_{k=1}^{+\infty} e^{itx_k}p_k \]
连续型
\[ g(t)=\int_{-\infty}^{+\infty}f(x)dx \]
性质
特征函数的导数和随机变量均值之间的关系 \[ g^{(k)}(0)=i^kEX^k \]
这个性质可以根据特征函数来求解随机变量的均值和方差。\(g’(0)=EX, g''(0)=EX^2.\)又\(DX=(EX)^2-EX^2\).
为了方便记忆,可以简单证明/验证一下这个性质:k=1时,\((Ee^{itX})'=E(iXe^{itX})|_{t=0}=iEX\)
若\(X_1,X_2,...X_n\)是相互独立的随机变量,则\(X=X_1+X_2+...+X_n\)的特征函数为
\[ g(t)=g_1(t)g_2(t)...g_n(t) \]
条件期望
\(E(X|Y)\)是随机变量Y的函数,也是随机变量,称为X在Y下的条件期望 \[ EX=E[E(X|Y)]=\int[E(X|Y=y)]dF_Y(y) \] 可以理解为条件期望再求期望是\(EX\).
随机过程的基本概念
有限维分布函数族
\[ \{F(n_1,n_2,...,n_m;x_1,x_2,...x_m)\} \]
一维分布函数族\(\{F(n,x)\}\)
n为给定常数,代入得到\(x(n)\)的一个具体的随机变量。再对这个随机变量求分布函数,由于是分布函数,所以所求概率一定是\(x(n)\)对应n较小的那一个。
二维分布函数族
两个一维分布函数族相乘就是二维分布函数族,但是要注意区间。
随机过程的数字特征
设\(X_T={X(t),t\in T}\)是随机过程
- 均值函数[重点]
\[ m_x(t)=EX(t) \]
注意对随机过程求均值实质上是对随机过程中的随机变量求均值。例如:对\(X(t)=sinUt\) 求均值,其中\(U\sim U(0,2\pi),U\)为均匀分布。 \(EX(t)=\frac{1}{2\pi}\int_{0}^{2\pi}(sinUt)du\)
- 协方差函数
\[ B_x(s,t)=E[\{X(s)-m_x(s)\}\{X(t)-m_x(t)\}] \]
- 方差函数
\[ D_x(t)=B_x(t,t)=E[X(t)-m_x(t)]^2 \]
- 相关函数[重点]
\[ R_x(s,t)=E[X(s)X(t)] \]
- 协方差和相关函数的关系[重点]
\[ B_x(s,t)=R_x(s,t)-m_x(s)m_x(t) \]
当\(m_x(t)\equiv 0\)时 \[ B_x(s,t)=R_x(s,t) \]
复随机过程
- 复随机过程的相关函数
\[ R_z(s,t)=E[Z_s \bar{Z_t}] \]
几种重要的随机过程
正交增量过程
共轭相乘的期望为0 \[ E[(X(t_2)-X(t_1))(\overline{X(t_4)-X(t_3)})]=0 \] 其中\(t_1<t_2\le t_3<t_4\)
注意相减的顺序,一定的按照顺序相减,不能出现\(t_n\)的顺序交叉相减
独立增量过程
不相重叠时间随机过程相减\(X(t_2)-X(t_1),X(t_3)-X(t_2),...,X(t_n)-X(t_{n-1})\)是相互独立的
平稳过程(重点)
考试中通常会出现给出一个随机过程,判断其是否为平稳过程。若满足如下两个条件,则为平稳过程。
- 对任意\(s,t \in T\),\(m_x(t)=EX(t)=常数\)
- 对任意\(s,t \in T\),\(R_x(s,t)=E[X(s)X(t)]=R_x(s-t)\)
相关函数只与‘s-t’有关
泊松过程
定义
泊松过程中,采用计数过程\(\{N(t),t\le0\}\) \[ P\{X(t+s)-X(s)=n\}=e^{-\lambda t}\frac{(\lambda t)^n}{n!} \] 其中,\(\lambda\)表示速率或强度
数字特征
\[ E[X(t)-X(s)]=D[X(t)-X(s)]=\lambda (t-s) \]
泊松过程均值和方差均相同
\[ B_x(s,t)=R_x(s,t)-m_x(s)m_x(t)=\lambda s \]
非齐次泊松过程
允许强度\(\lambda(t)\)为\(t\)的函数,\(\lambda(t)\)不是一个常数
均值函数 \[ m_x(t)=\int_{0}^{t}=\lambda(s)ds \]
t时刻对强度进行求和
非齐次泊松过程的函数
\[ P\{X(t+s)-X(t)=n\}=\frac{[m_x(t+s)-m_x(t)]^n}{n!} e^{-[m_x(t+s)-m_x(t)]} \]
或者更常用的化简后的公式为 \[ P\{X(t)=n\}=\frac{[m_x(t)]^n}{n!} e^{[-m_x(t)]} \]
复合泊松过程
定义
\({N(t),t\le 0}\)是强度为\(\lambda\)的泊松过程,\(Y_k\)是一列独立同分布的随机变量 \[ X(t)=\sum_{k=1}^{N(t)} Y_k, \quad t\le0 \]
数字特征
复合泊松过程的期望和方差为
\[ E[X(t)]=\lambda t E[Y_1] \]
\[ D[X(t)]=\lambda t E[Y_1^2] \]
马尔可夫链
- 定义
未来处于哪个状态的概率只与现在有关,而与过去无关 \[ P\{X_{n+1}=i_{n+1}|x_0=i_0,x_1=i_1,...,x_n=i_n\}=P\{X_{n+1}=i_{n+1}|x_n=i_n\} \]
转移概率
一步转移概率
\[ P_{ij}=P\{X_{n+1}=j|X_n=j\} \]
\(P_{ij}\)表示由 \(i\) 转移到 \(j\) 的概率
一步转移概率矩阵为 \[ \boldsymbol{P}=\left(\begin{array}{ccccc} p_{11} & p_{12} & \cdots & p_{1 n} & \cdots \\ p_{21} & p_{22} & \cdots & p_{2 n} & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right) \]
- 性质
- \(p_{ij} \ge 0\)
- \(\sum_{j \in I} p_{ij}=1\) 行和为1
n步转移概率
\[ p_{ij}^{(n)}=P\{X_{m+n}=j|X_n=i\} \]
n步转移矩阵 \[ P^{(n)}=(p_{ij}^{(n)}) \]
n个一步转移矩阵相乘
性质(C-K方程)
- \(p_{ij}^{(n)}=\sum_{k \in I}p_{ik}^{(l)}p_{kj}^{(n-l)}\)
- \(P_{ij}^{(n)}=\sum_{k_1 \in I}...\sum_{k_{n-1} \in I} p_{ik_1}p_{k_1 k_2}...p_{k_{n-1}j}\)
中间状态的转移可能有多种情况
马尔可夫链状态的分类
\[ \left\{ \begin{array}{lc} 非常返态(f_{ii}<1) \\ 常返态(f_{ii}=1) \left\{ \begin{array}{lc} 零常返(\mu_{ii}= \infty) \\ 正常返(\mu_{ii}<\infty) \left\{ \begin{array}{lc} 有周期(d>1) \\ 非周期(d=1)——遍历态 \end{array} \right. \end{array} \right. \end{array} \right. \]
请注意,常返态和周期性是对于状态来说的,但一个状态空间的子集中,常返性和周期性是相同的。
常返和非常返
- 首中概率:定义由\(i\)出发首次到达\(j\)的概率 \(f_{ij}=\sum_{n=1}^{\infty}f_{ij}^{(n)}\)
\[ \left\{ \begin{array}{lc} f_{ii}=1 \quad i为常饭 \\ f_{ii}<1 \quad i为非常返 \end{array} \right. \]
- 期望值 \[ \mu_i=\sum_{n=1}^{\infty}n f_{ii}^{(n)} \] 这个表示由出发\(i\)再返回\(i\)的平均时间 \[ \left\{ \begin{array}{lc} 零常返(\mu_{ii}= \infty) \\ 正常返(\mu_{ii}<\infty) \end{array} \right. \]
周期
\[ \left\{ \begin{array}{lc} 有周期(d>1) \\ 非周期(d=1) \end{array} \right. \]
互通
若\(i\)可达\(j\),\(j\)可达\(i\),则\(j\)称\(i\)与互通,记为\(i\longleftrightarrow j\)
状态空间分解
一些重要概念
- 闭集:状态不能转移出闭集
- 若C中所有状态互通,则称C为不可约闭集
- 若马氏链\(\{X_n\}\)的状态空间\(I\)是不可约闭集,则称\(\{X_n\}\)是不可约马尔科夫链。
状态空间分解的原则
任一马氏链的状态空间\(I\),可唯一地分解成有限个或可列个互不相交的子集\(D,C_1,C_2,...\)之和 \[ \left\{ \begin{array}{lc} (1) 每一C_n,n=1,2,...是\mathbf{常返态}组成的\mathbf{不可约闭集} \\ (2) C_n,n=1,2,...中的\mathbf{状态同类},即或全是\mathbf{正常返},或全是零常返,它们具有\mathbf{相同的周期},且f_{ik}=1,j,k \in C_n \\ (3) D由全体非常返态组成 \end{array} \right. \]
从这里可以看出来每个闭集中都有相同的周期和常返性。所以在题目中让判断每一个状态的性质的时候,只需要判断每一个闭集中的常返性和周期即可
平稳分布
\[ \left\{ \begin{array}{lc} \pi_j=\sum_{j \in I} \pi_i p_{ij} \quad\\ \sum_{j \in I} \pi_j=1 \end{array} \right. \]
第一行公式中,\(i\)为行,\(j\)为列,这个公式表示第\(j\)列的概率
第二行公式中,表示所有的\(\pi_j\)相加和为1
推论1:有限状态不可约非周期马尔可夫链必存在平稳分布
推论2:若不可约马尔科夫链的所有状态是非常返或零常返的,则不存在平稳分布
推论3:若\(\{\pi_j,k\in I\}\)是不可约非周期马尔科夫链的平稳分布,则 \[ \pi_j=\frac{1}{\mu_j} \]
可以用于求各状态的平均返回时间
一些例题
随机过程基本概念
分布函数族


本题为2022-2023 第二学期 期末考试原题
验证平稳分布
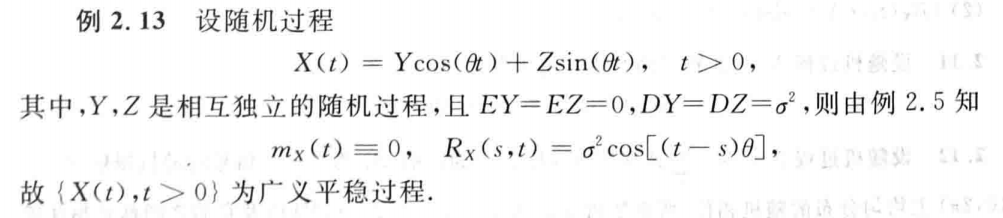
泊松过程
非齐次泊松过程求解

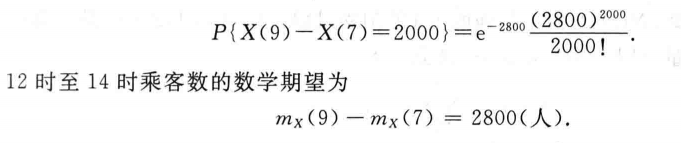
验证是否为泊松过程

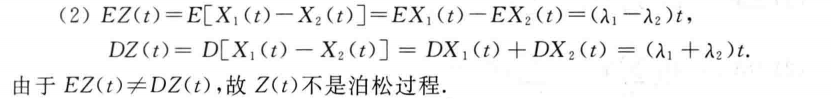
本题为 2022-2023 第二学期 期末考试原题
马尔可夫链
天气预报问题

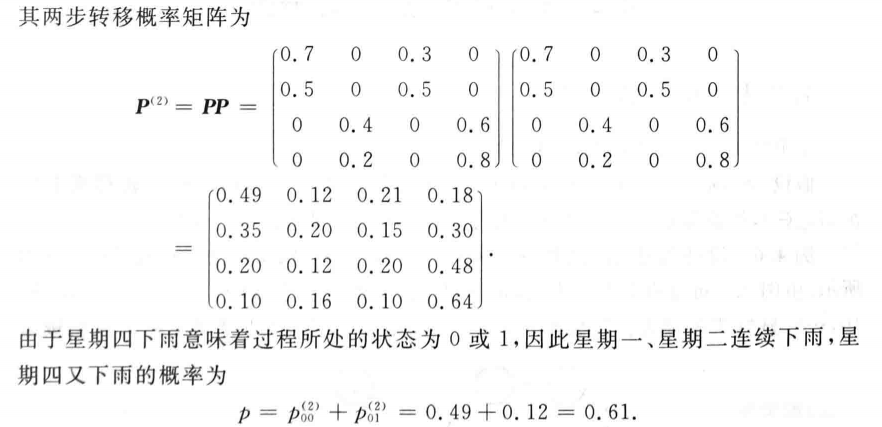
本题为 2022-2023 第二学期 期末考试原题
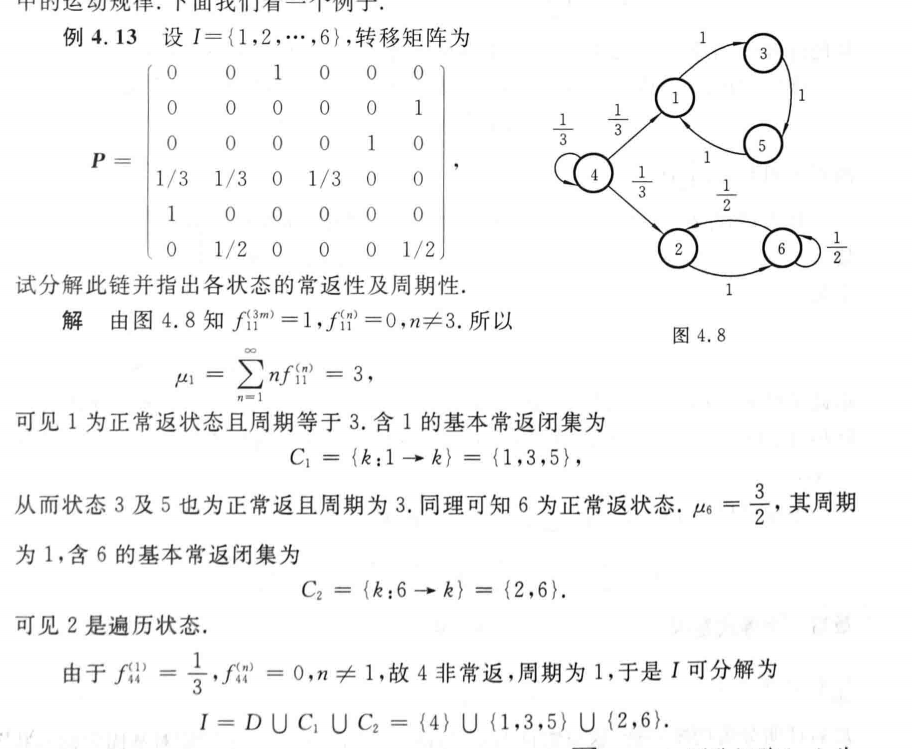
状态空间分解,判断每个状态性质
求平稳分布和平均返回时间
