01. 存储结构:数列和链表

本文最后更新于 2025年9月1日上午

存储结构:数列和链表

术语

数据项
数据项是数据中的最小单位，通常用来描述一个属性。
数据元素
数据元素是数据的基本单位，在计算机中常作为一个整体来处理。一般来说，一个数据元素由多个数据项组成，具体包含哪些数据项取决于用户的需求。
数据对象
数据对象是具有相同属性（数据项的类）的数据元素的集合，是数据的一个子集。在实际应用中，被处理的是数据元素通常具有相同的属性，在不产生混淆的前提下，数据对象简称为数据。
数据结构
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。在任何问题中，数据对象中的数据元素都不是孤立存在的，而是相互之间存在着某种关系，这些关系称为结构。良好的数据结构可以给程序带来更高的运行/存储效率。
数据对象上的关系指属于同一对象的数据元素之间的关系。可以用$<a,b>$俩表示数据元素$a$，$b$之间的前驱后继关系，$a$是$b$的前驱，$b$是$a$的后继。
- 数据的逻辑结构
  逻辑结构指的是从具体问题抽象出来的数学模型。它研究的是数据之间的逻辑关系，通常将逻辑结构分为四种类型：
  - 集合
    集合中的数据元素除了同属于一个数据对象外，别无其他关系；
  - 线性
    集合中的数据元素除了同属于一个数据对象外，存在一对一的关系；
  - 树
    集合中的数据元素除了同属于一个数据对象外，存在一对多的关系；
  - 图
    集合中的数据元素除了同属于一个数据对象外，存在多对多的关系；

抽象数据类型

抽象是指忽略研究对象的具体或者是无关的特性，只抽取其一般或者相关特性的过程。抽象是简化复杂现实问题的有效途径。抽象数据类型一般可以由数据对象、数据对象上的关系以及对数据对象的一组基本操作三个要素来定义。
抽象数据类型就是把具体的问题分解为多个小规模而且容易处理的问题，然后建立起计算机能够处理的数据模型，把每个功能模块的实现细节作为一个独立的单元，并将具体实现过程隐藏起来。
比如，函数的设计体现了抽象的思想，对函数的调用者而言，不必关心函数的具体实现过程，即函数将具体的实现过程给隐藏了起来。

数组和链表

存储结构

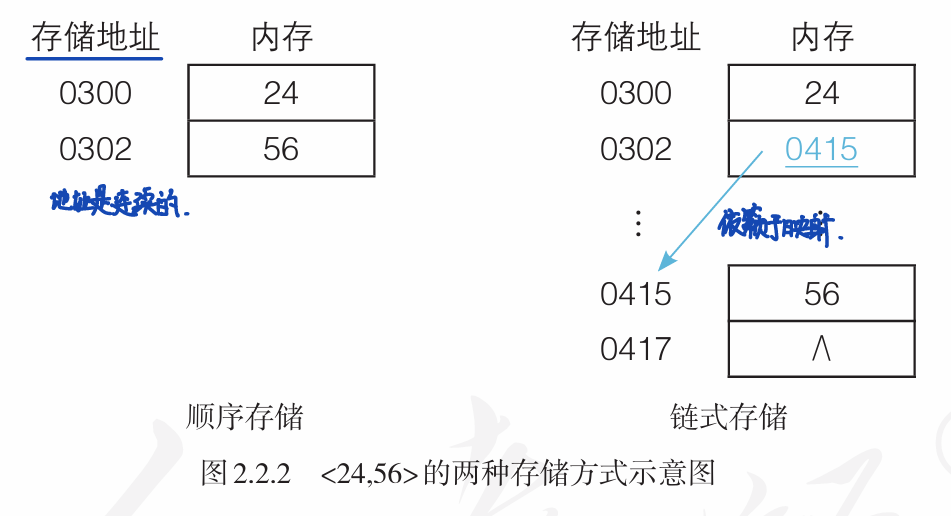
存储结构/物理结构指的是逻辑结构在计算机中的存储形式，存储结构包括顺序存储结构（数组）和链式存储结构（链表）.

顺序结构是把逻辑上相邻的数据元素存放在地址连续的若干存储单元中，数据元素之间的逻辑关系由存储单元的邻接关系实现。在顺序结构中，只需要存储数据元素的数据域Data即可。
链式存储结构是指把数据元素存放在任意的存储单元中，这些存储单元可以是连续的，也可以是不连续的。链式存储结构在高级程序设计语言中通常用指针来实现。在链式存储结构中，每个数据元素除了要存放其数据域之外，还要存放其后继元素的存储地址（指针域）。
DataNext Address

数组

数组是一组具有相同数据类型的数据元素的集合，占用一段连续的存储空间，常用来实现数据的顺序存储。
#### 数组的操作

插入和删除元素
在某一个数组中插入：
- 如果插入，则直接将现在数组的后面一个索引对应的元素进行赋值就好。
- 如果插入，那么插入。

由于数组在内存中占用的是一段连续的存储空间，一旦在程序中定义了数组，那么它的维度和能够容纳的元素个数就不会轻易地发生改变。因此对数组经常进行存取和查找操作，一般不进行数组的插入或者删除操作。
数组的优点和缺点都在于元素存储的集中方式和连续性。它的缺点具体表现为数组元素的插入和删除需要大量移动数组中已有的元素，当数组中存储的数据元素个数较多时，操作量将会很大。

链表

链表指由多个节点（由数据域和指针域组成）链接成的序列，通过节点的指针域将多个节点按数据元素的逻辑顺序链接在一起。每个节点只有一个指向后继的指针域的链表称为单链表。通常，我们将链表示意为用箭头相链接的节点的序列，节点之间的箭头表示指针域中的指针。假设有一个由$n$（$n$ 为正整数）个数据元素构成的线性结构$（a_1，a_2，…，a_i，…，a_n）（1 ≤ i ≤ n）$，则由$ n$ 个节点链接成的单链表如下图所示，其中，Head指示链表中第一个节点的存储位置，称为头指针。尾部一般用Null表示。

链表的操作

定义结点类

class None(object):
    def __init__(self,data,next=None):
        self.data = data #数据域
        self.next - next # 指针域

初始化链表

class LinkList(object):
  def __init__(self):
      self.head = None

  def initlist(self):
      data = input() # 链表中每个节点的数据通过输入获得
      if data != "-1": # 输入-1时表示链表结束
          self.head = Node(int(data))
          p = self.head # 初始化指针
      while data != '-1':
          data = input()
          if data == "-1":
              break
          else:
             p.next = Node(int(data)) # 由于Python的特性，Python自己其实是没有指针的，这里这个object自己就是data的内存地址
             p = p.next # 指针后移一位

求链表长度/遍历链表节点从链表的头指针开始，使用while，指针逐渐后移，直到指针遇到None：

def find_length(self):
  p = self.head
  length = 0
  while p != None:
      length = length + 1
      p = p.next
  return length

查找节点
从链表的头指针开始查找，验证边界条件：如果是空链表则返回链表为空，当链表为空时则使用while对每个节点的数据域注意比较：

def search(self, value):
  if self.find_length() == 0:
      print('empty linked list')
      return
  p = self.head
  i = 0
  while p.next != None and p.data !=value:
      p = p.next
      i = i+1
  if p.data == value:
      print('find value in position:', i+1)
  else:
      print('no such value')
  return

链表的问题在于，如果要查找链表里面的一个元素，链表必须从头开始遍历。其时间复杂度最高是$O(n)$。

插入节点
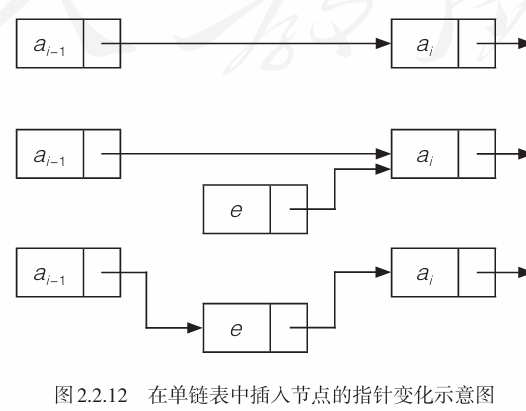
在一个有$n$个节点的链表中插入一个结点$e$使其成为第$i$个节点的基本步骤是：

查找定位$a_{i-1}$
生成一个新的节点$e$
调整指针：当$i\neq1$时，首先将$e$的后继指针指向$a_i$，然后再将$a_{i-1}$的后继指针指向$e$

  def insert(self,index,item):
    p = self.head
    # 如果把增加的节点放在第一个位置，那么只用处理后面一个结点
    if index == None:
        q = Node(item)
        q.next = self.head
        self.head = q
    else:
        post = self.head
        # 遍历整个链表，找到index -1 的位置
        while p.next != None and j< index:
            post = p
            p = p.next
            j = j+1
        # 对index -1位置处的节点指针进行修改
        if index == j:
            q = Node(item,p)
            post.next = q
            q.next = p

- 删除节点   
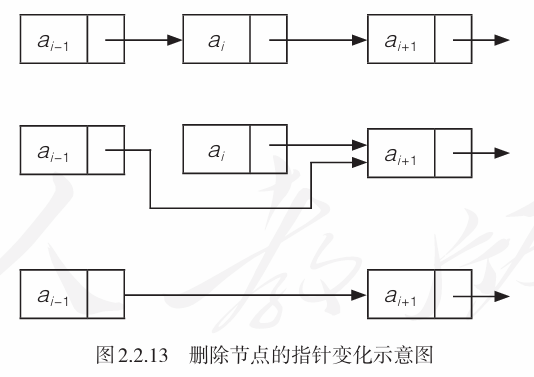
  在有$n$个节点的单链表中删除第$i$个数据元素$a_i$的基本操作是：  
  1. 查找定位$a_{i-1}$  
  2. 修改指针    
  <img src=https://cdn.jsdelivr.net/gh/l61012345/Pic//img/20250615151117733.png width=40%>    

  ```python
  def delete(self,index):
    p = self.head
    if index == None: # 如果删除的是第一个节点
        q = self.head
        self.head = q.next # 头改为第一个节点指针域的内容
        p = self.head
    else:
        post = self.head
        j  = 0
        while p.next != None and j<index:
            post = p
            p = p.next
            j = j + 1
        if index == j:
            post.next = p.next

从上面的代码可以看出，使用链表会很方便地动态增删数据，无需考虑数据容器的大小。只用调整目标附近的索引就行了。

对比

因此，对数据元素进行的操作主要是查找，很少涉及插入和删除的时候，应该采用数组作为存储结构。如果需要频繁的对数据元素进行增删，则应当使用链表结构。
当程序中需要的元素个数变化较大或者不知道数据量有多大时，建议选择链表结构，这样可以不需要考虑存储空间大小的问题。但如果事先知道元素的大致个数，采用数组的效率会高很多。

	数组	链表
存储分配	数组用一段地址连续的存储单元依次存储数据元素	链表用一组地址不要求连续的存储单元存放数据元素，用指针来反映数据元素之间的逻辑关系
空间性能	数组需要一段连续的存储空间，因此对内存的要求较高；存储密度高	链表不需要一段连续的存储空间，因此对内存的要求不高；存储密度低
时间性能	数组是一种随机访问结构，对数组中任一元素都可以直接存取。而在数组中进行插入和删除，平均要移动近一半的元素，当每个元素的信息量较大时，移动元素需要消耗较长的时间。	链表是一种顺序访问结构，要查找链表中的任一元素，都需从头指针起开始查找，平均需要搜索半个链表。而在链表中的任何位置上进行插入和删除，都只需要修改指针，不需要移动元素

使用线性搜索时数组和链表的时间复杂度如下表所示：

	数组	链表
`search(x)`	$O(n)$	$O(n)$
`insert(x)`	$O(1)$ 在末端插入	$O(1)$ 在头部插入
`remove(x)`	$O(n)$	$O(n)$

学习笔记 > 数据结构

01. 存储结构:数列和链表

https://l61012345.top/2025/08/28/学习笔记/数据结构/存储结构_数列和链表/

作者

Oreki Kigiha

发布于

2025年8月28日

更新于

2025年9月1日

许可协议

02. 线性逻辑结构：栈和队列上一篇

笔记摘要-涌现：从混乱到秩序下一篇

	数组	链表
`search(x)`	\(O(n)\)	\(O(n)\)
`insert(x)`	\(O(1)\) 在末端插入	\(O(1)\) 在头部插入
`remove(x)`	\(O(n)\)	\(O(n)\)