02. 线性逻辑结构：栈和队列

本文最后更新于 2025年9月1日 上午

线性逻辑结构：栈和队列

栈

栈(stack)是一种线性的抽象数据结构，只允许在有序的线性资料集合的一端（称为堆栈顶端，top）进行加入数据（push）和移除数据（pop）的运算。因而按照后进先出（LIFO, Last In First Out）的原理运作，堆栈常用一维数组或链接串列来实现。
栈的基本操作包括：

  • pop：弹出栈顶的元素
  • push：将数据元素放入栈顶
  • top：返回栈顶
  • IsEmpty：判断栈是否为空

上面的这些基本操作的时间复杂度都是\(O(1)\)。
栈在计算机中的应用包括：

  • 函数的调用和递归
  • 文字编辑器中的“撤销”（Undo）
  • 检查公式/程序的括号是否匹配

栈的实现

数组的实现方式

用数组来实现栈的方式非常直接，即指定某个数组A的起始开始到某一索引对应元素的区域为这个栈，栈顶为最后一个索引对应的元素。

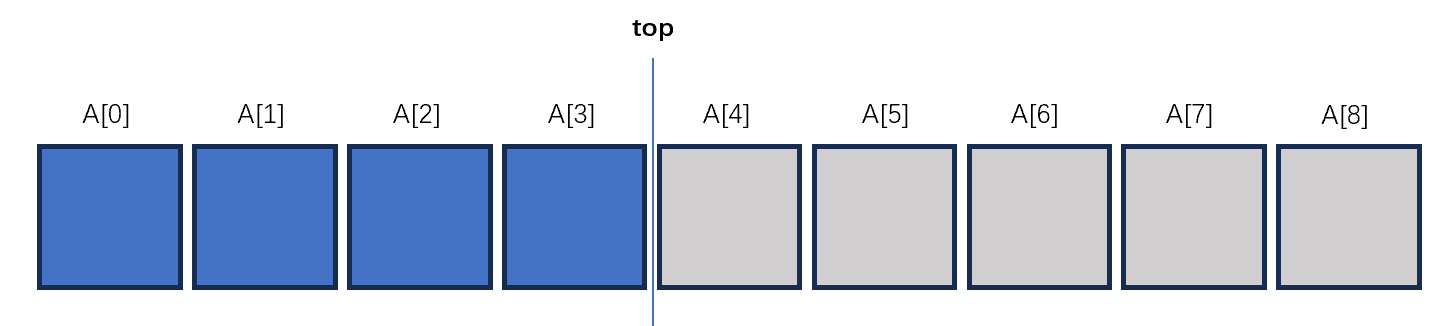
在数组下来看上面提到的基本操作：

  • 检查栈空：
    可以人为设定当top返回的索引值为-1时表示栈空。
    1
    2
    3
    4
    5
    IsEmpty(){
      if (top=-1):
      return True
      else return False
    }
  • push
    设定栈顶的索引对应元素的值为新加入的值，同时top的索引向右移动一位。
    1
    2
    3
    4
    push(x){
      top = top + 1
      A[top] = x
    }
    需要注意的是，在C/C++语言中数组有可能添加的数据会超过数组的大小，此时会发生栈溢出。比较好的解决方法是在现有数组满的情况下重新创建一个两倍大的数组，然后把原来数组中的内容复制到新的数组中。
  • pop
    top的索引向左移动一位。原来的数据变为垃圾数据。
    1
    2
    3
    pop(x){
      top = top -1
    }
  • top 返回top对应索引的值。
    1
    2
    3
    top(){
      return A[top]
    }

完整的C++实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// Stack - Array based implementation
 
#include <stdio.h>
 
#define MAX_SIZE 10
int A[MAX_SIZE];	//数组声明括号里的数指的是元素个数
int top = -1;
 
void Push(int x)
{
	if(top == MAX_SIZE-1){
		printf("Error: Stack overflow\\n");
		return;
	}
	A[++top] = x;	//先自增再赋值 
}
 
void Pop()
{
	if(top == -1){
		printf("Error: No element to pop\\n");
		return;
	} 
	top--;	//Pop元素不用管，下次赋值自动更新 
}
 
int Top()
{
	return A[top];
}
 
void Isempty()
{
	if(top == -1)	printf("Stack is empty.");
	else printf("Stack is not empty.");
}
 
void Print()
{
	printf("Stack is:");
	for(int i=0;i<=top;i++){
		printf("%d ",A[i]);
	}
	printf("\\n");
}
 
int main()
{
	Push(2);	Print();
	Push(5);	Print();
	Push(10);	Print();
	Pop();	Print();
	Push(12);	Print();
	Isempty();	
	
	return 0;
}
#### 链表的实现方式
回忆链表的基本结构：
头部head是一个指向第一个数据元素地址的指针，每个节点（数据元素）包括数据和指针两个域，数据域是这个节点的数据，指针域则是下一个节点的地址，最后一个节点的指针域指向Null。
在链表下来看栈的基本操作：
对于添加和删除元素，在栈里面可以实现的方法有两种：将链表的头部/尾部视为栈顶，从而从链表的头部/尾部添加或者删除元素。
无论是哪一种，操作方法都与链表元素的增删没有差别。

  • 从链表的尾部增删元素时，由于链表自身的特性，需要遍历整个列表之后才能够找到链表最后一位插入的位置，因此从链表的尾部进行增删元素的时间复杂度为\(O(n),n\)为链表的元素个数。
  • 从链表的头部增删元素时，无需遍历，只需要将原来头部指针指向的地址作为新增加的元素的指针域地址，同时修改头部指针的地址即可，这样的操作时间复杂度是常数\(O(1)\)。

因此用链表实现栈时，一般都是将链表的头部视为栈顶。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// Stack - linked list based implementation
 
#include <stdio.h>
#include <stdlib.h>
// 定义节点类型
struct Node
{
	int data;
	struct Node* next;
};
struct Node* top = NULL;
 
void Push(int x)
{
	struct Node* temp;
	temp = (struct Node*)malloc(sizeof(struct Node));
	//malloc是c语言中在堆中动态分配内存的方式
    temp.data = x;
	temp.next = top;
	top = temp;
}
 
void Pop()
{
	if(top == NULL)	return;
	struct Node* temp = top;
	top = top.next;
	free(temp);
}
 
void Print()
{
	struct Node* temp = top;
	printf("Stack is:");
	while(temp != NULL){
		printf("%d ",temp.data);
		temp = temp.next;
	}
	printf("\\n");
}
 
int main()
{
	Push(2);	Print();
	Push(5);	Print();
	Push(10);	Print();
	Pop();	Print();
	Push(12);	Print();
	
	return 0;
}

栈的使用

反转

栈可以用来反转列表或者是链表，比如如果要反转一个字符串，则将字符串中的字符按照顺序填入栈中，填完后再依次出栈即可。对于链表的显式反转也可以用同样的方法来实现。
链表的反转还可以进行隐式的操作：

1
2
3
4
5
6
7
8
9
10
//假设有一个栈s
Node *temp = s.top(); 
head = temp;
s.pop();
while (!s.IsEmpty()){
    temp.next = s.top(); //将链表中元素指向的下一个节点设置为栈顶
    s.pop();
    temp = temp.next;
}
temp.next = NULL;
完整代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// Using stack to reverse a linked list
#include<iostream>
#include<stack>
using namespace std;
 
struct Node
{
	int data;
	struct Node* next;
};
struct Node* head = NULL;
 
void Reverse()
{
	if(head == NULL)	return;
	stack<struct Node*> S;
	struct Node* temp = head;
	while(temp != NULL){
		S.push(temp);
		temp = temp.next;
	}
	temp = S.top();
	head = temp;
	S.pop();
	while(!S.empty()){
		temp.next = S.top();
		S.pop();
		temp = temp.next;
	}
}
#### 检查括号的匹配 检查括号匹配的意思是，对于一个数学表达式例如{(A+B)+(C+D)}，检查表达式的每一个括号的左括号和右括号是否匹配的任务，检查需要满足：

  1. 括号的数量相同
  2. 括号的顺序相同

解决办法是：

  1. 对数学表达式从左边到右边进行扫描
  2. 如果遇到一个左括号，那么将左括号加入到一个列表中
  3. 如果遇到一个右括号，则将列表中的左括号元素移除
  4. 最后检查列表是否为空

可以发现这个列表是需要遵循后进先出的原则的，因此可以用栈来实现这个列表，伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
CheckBlank(exp){
    n = length(exp);
    create a stack s;
    for i=0 to n-1:
    {
        if exp[i] is "(" or "[" or "{":
        {
            push(exp[i]);
        }
        else if exp[i] is ")" or "]" or "}":
        {
            if (s.IsEmpty()):{
                return False; //栈顶没找到匹配的符号
            }
            else 
            {
                pop();
            }
        }
        if s.IsEmpty():{
            return True // 遍历完成后栈是空的，表明所有括号都是匹配的
        }
        else{
            return False
        }

    }
}
C++的完整代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/*
  C++ Program to check for balanced parentheses in an expression using stack.
  Given an expression as string comprising of opening and closing characters
  of parentheses - (), curly braces - {} and square brackets - [], we need to 
  check whether symbols are balanced or not. 
*/
#include<iostream>
#include<stack>
#include<string>
using namespace std;
 
// Function to check whether two characters are opening and closing of same type. 
bool ArePair(char opening, char closing)
{
	if(opening == '(' && closing == ')')	return true;
	else if(opening == '[' && closing == ']')	return true;
	else if(opening == '{' && closing == '}')	return true;
	else	return false;
}
 
bool AreParanthesesBalanced(string exp)
{
	stack<char> S;
	for(int i=0;i<exp.length();i++){
		if(exp[i]=='(' || exp[i]=='[' || exp[i]=='{')
			S.push(exp[i]);
		else if(exp[i]==')' || exp[i]==']' || exp[i]=='}'){
			if(S.empty() || !ArePair(S.top(),exp[i]))
				return false;
			else	S.pop();	
		}
	}
	return S.empty() ? true : false;
}
 
int main()
{
	string expression;
	cout << "Enter an expression: ";
	cin >> expression;
	if(AreParanthesesBalanced(expression))
		cout << "Balanced";
	else
		cout << "Not balanced";
}
#### 算术求值 ##### 前缀、中缀、后缀表达式 前缀、中缀、后缀表达式是数学表达式的三种不同的写法，它们的结构表示如下：

  • 中缀表达式：<operand><operator><operand>
    在中缀表达式下需要检查算术优先级和括号
  • 前缀表达式：<operator><operand><operand>
  • 后缀表达式：<operand><operand><operator>

前缀表达式和后缀表达式都是没有歧义的书写方法，都不用检查算术优先级和括号，因此对机器更加友好。

后缀表达式和前缀表达式的求值

以后缀表达式为例，如果将一个后缀表达式按照顺序填入一个列表中，在放入列表的过程中，如果遇到operator那么列表就将之前最近的放入列表的两个operands提出，并且将运算结果返回列表中。可以发现对这个列表的操作是从同一端放入和取出元素的，因此这个列表其实是一个栈。
下面的图展示了一个后缀表达式运算的例子：

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
EvaluatePostfix(exp):{
    create a stacks;
    for i=0 to length(exp)-1:{
        if (exp[i] is operand):{
            push(exp[i]);
        }
        else if (exp[i] is operator):{
            op1 = pop();
            op2 = pop();
            result = Perform(exp[i],op1,op2);
            push(result);
        }
    }
}
那么前缀表达式的求值计算也是同理，只不过放入栈中的顺序从从左到右变成了从右到左。
下面展示了一个例子：

中缀表达式转后缀表达式

中缀表达式转后缀表达式的基本思想是： 将中缀表达式按照从左到右的顺序把符号放入栈中，如果栈上的操作符优先级比正在遍历的符号的优先级更高，那么它可以弹出栈并且放入后缀表达式中（因为不确定正在遍历的运算符右边的运算数是什么）。

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
InfixToPostfix(exp):{
    create a stack s;
    for i=0 to length(exp)-1:{
        if exp[i] is operand:{
            result.append(exp[i]);
        }
        else if exp[i] is operator:{
            while (! s.IsEmpty() and HasHigherPriority(s.top(),exp[i])){
                result = result.append(s.top());
                s.pop();
            }
            s.push(exp[i]) //遍历结束的时候把所有剩下的符号全部入栈
        }
    }
    while(! s.IsEmpty()){
        result = result.append(s.top())
        s.pop()
    }
    return result
}

在考虑括号的情况下，还需要指定如下规则：

  • 运算符入栈时：
    若栈顶为左括号 (，则当前运算符不出栈比较优先级，直接入栈。

  • 运算符出栈时：
    弹出操作会一直进行，直到遇到左括号为止，左括号本身不出栈。

  • 遇到右括号 ) 时：
    将栈顶元素依次弹出并加入后缀表达式，直到弹出左括号 ( 为止（左括号本身丢弃，不加入后缀表达式）。

下图展示了一个例子：

这个部分伪代码如下：(【】里面的内容为新加的)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
InfixToPostfix(exp):{
    create a stack s;
    for i=0 to length(exp)-1:{
        if exp[i] is operand:{
            result.append(exp[i]);
        }
        else if exp[i] is operator:{
            while (! s.IsEmpty() and HasHigherPriority(s.top(),exp[i]) 【And !IsOpeningParenthesis(s.top())】){
                result = result.append(s.top());
                s.pop();
            }
            s.push(exp[i]) //遍历结束的时候把所有剩下的符号全部入栈
        }
        【
        else if IsOpeningParenthesis(exp[i]):{
            s.push(exp[i]);
        }
        else if IsClosingParenthesis(exp[i]):{
            while(!s.IsEmpty() And !IsOpeningParenthesis(s.top())){
                result = result.append(s.top());
                s.pop();
            }
            s.pop();
        }
        】
    }
    while(! s.IsEmpty()){
        result = result.append(s.top())
        s.pop()
    }
    return result
}

队列

队列是一种特殊的列表，遵循先进先出原则，插入和删除元素的操作只能在这个列表的分别一段进行。
队列可以进行的基本操作接口如下：

  • Enqueue(x)：插入元素
  • Dequeue(x)：删除元素
  • Front(x)：返回队列头元素
  • IsEmpty：是否为空队列

这些基本操作都具有常数的时间复杂度\(O(1)\).
在计算机中，队列常用于：

  • 资源分配，在一次只能给一个资源的情况下分配请求资源
  • 模拟等待
  • 调度

队列的实现方式

数组实现队列

用数组实现队列的方式是取一个数组的中间两端，分别作为队首和队尾。
那么创建队列的方式则是直接创建一个数组，并初始化队首和队尾指向的索引，可以令空队列时队首和队尾的索引值为-1，例如下面的操作：

1
2
3
int A[10]
front = -1;
rear = -1;
现在来看刚才提到的队列的基本操作利用数组的实现方式，需要注意这些操作都需要满足常数时间复杂度的要求。

  • IsEmpty
    检查队首和队尾指向的索引是否为-1。

    1
    2
    3
    4
    5
    6
    7
    8
    IsEmpty(){
      if front == -1 and rear == -1:{
          return True
      else{
          return False
      }
      }
    }

  • Enqueue
    先检查边界条件：如果队列已经满了的话那么不会添加这个元素；如果队列为空的话需要先调整front和rear的索引值。其他情况下只需要将当前的rear指向的序列索引填入内容后，移动rear指向下一个索引即可。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    Enqueue(x){
      if IsFull():{
          return
      }
      else if IsEmpty():{
          front =  rear = 0;
          A[rear]=x;
      }
      else{
          rear = rear + 1;
          A[rear] = x;
      }
    }

  • Dequeue
    出队之前需要检查这个元素离开之后队列是否变成空队列，或者这个队列本身是否为空队列；其他情况下只需要将队首索引向后移动一个就可以，这时删除的数据仍然在数组中，但是变成垃圾数据。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    Dequeue(x){
      if IsEmpty(){
          return
      }
      else if front == rear // 这是队列中的最后一个元素{
          front = rear = -1;
      }
      else{
          front = front + 1;
      }
    }
    ##### 数组实现循环队列 循环队列是一种特殊的队列，这种队列的首尾是相连接的。在循环队列中，队首和队尾的指示变成对下一个位置的指示，假设一个最大元素为\(N\)的队列，现在的位置为\(i\)，那么下一个位置表示为：
    \[(i+1)mod N\] 利用取余数，当标号到\(N-1\)(因为是从0开始的)时下一个位置便会为0.
    这时候需要对入队和出队做一些小小的修改：

  • Enqueue

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    Enqueue(x){
      if (rear+1)%N==front:{ //队尾和队首标号相同，代表队列满了
          return
      }
      else if IsEmpty():{
          front =  rear = 0;
          A[rear]=x;
      }
      else{
          rear = (rear + 1)%N; // 下一个索引
          A[rear] = x;
      }
    }

  • Dequeue

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    Dequeue(x){
      if IsEmpty(){
          return
      }
      else if front == rear // 这是队列中的最后一个元素{
          front = rear = -1;
      }
      else{
          front = (front + 1)%N; //上一个索引
      }
    }

链表实现队列

用数组实现队列的问题在于数组无法动态分配大小，数组被占满之后需要做一些额外的操作（将现在数组里面的元素复制到一个更大的数组中），因此在需要动态分别大小的情况可以用链表来实现队列。
可以将链表的两头分别作为队尾和队首来模拟队列。
但是链表的遍历过程存在一个问题：从链表的尾部插入或者删除元素所需要的时间复杂度是\(O(n)\)，并不符合队列中基础操作都消耗常数时间复杂度\(O(1)\)的要求。
解决这个问题的办法是在创建链表时就给这个链表赋予两个指针，front和rear分别指向链表的头部和尾部。
下面是Enqueue和Dequeue的C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
struct Node{
    int data;
    struct Node* next;
};
struct Node* front = NULL;
struct Node* rear = NULL;
void Enqueue(int x){
    // 创建一个临时节点指针，malloc表示这个指针是在动态存储区创建的
    struct Node* temp=(struct Node*)malloc(sizeof(struct Node*));
    temp.data = x;
    temp.next = NULL;
    if (front == NULL) && (rear == NULL){
        front = rear = temp;
        return;
    }
    rear.next = temp;
    rear =  temp;
}

void Dequeue{
    struct Node* temp=front;
    if (front == NULL) return;
    if (front == rear){ //如果队列里面就这一个元素
        front = rear = NULL;
    }
    else{
        front = front.next;
    }
}

学习笔记 > 数据结构
02. 线性逻辑结构：栈和队列
https://l61012345.top/2025/08/29/学习笔记/数据结构/线性逻辑结构_栈和队列/
作者
Oreki Kigiha
发布于
2025年8月29日
更新于
2025年9月1日
许可协议