03. 非线性逻辑结构:树和图
本文最后更新于 2026年2月26日 晚上
非线性逻辑结构:树和图
树
数组、链表、栈、队列都是线性数据结构,树和图是非线性结构。在选择不同数据结构的时候应当考虑:
- 存储对象的类型
- 基本操作的开销
- 内存使用情况
- 实现的难易程度
术语
树是单向链接在一起的节点的集合,具有层级结构。
树中的基本数据单元是节点,节点和节点之间通过连结相连。树的最顶端的节点称为根节点。对于每个节点,与其相连接的节点称为这个节点的子节点;这个节点与其上层相连接的节点称为这个节点的父节点。同一个父节点的子节点之间称为兄弟节点(sibling nodes)。没有子节点的节点称为这个树的叶节点。
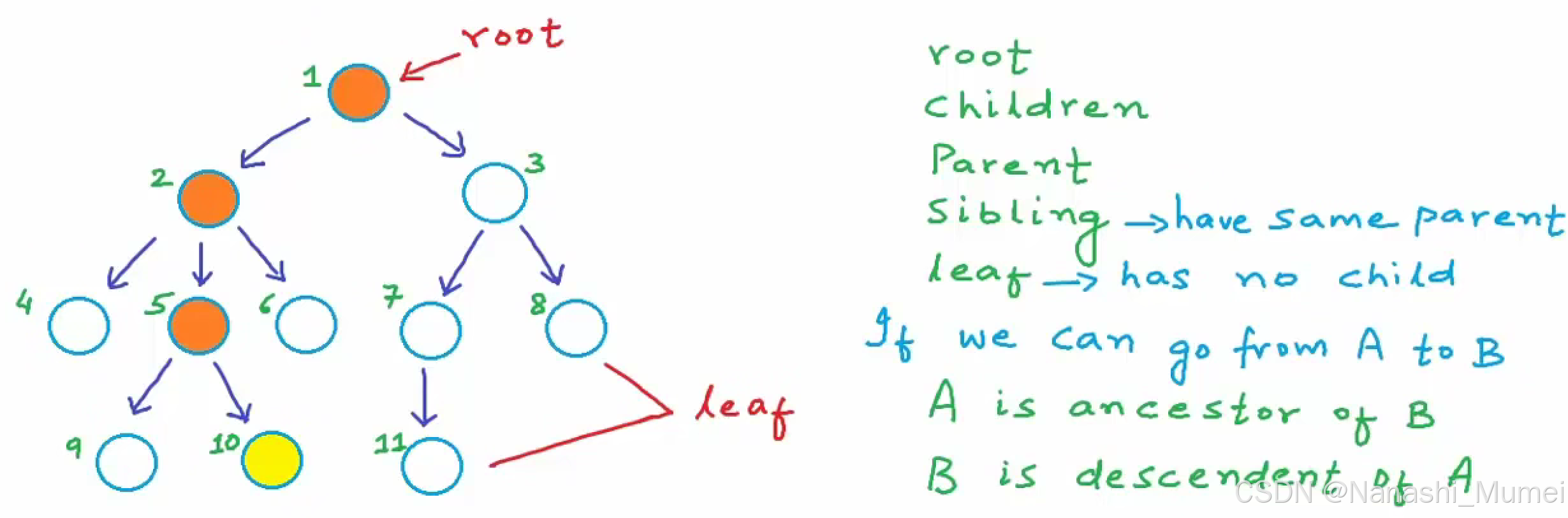
在计算机系统中,树可以用于:
- 组织文件系统
- 网络路由
- 组织数据以便快捷的搜索
树的性质
树是一种具有递归性质的数据结构,任何一个结点下方的所有子孙结点构成了以这个节点为根节点的子树。
一个具有\(N\)个节点的树具有\(N-1\)个连结。
从根节点到某个节点的路径长度称为这个节点的深度,根节点的深度为0.
从某个节点到一个叶子节点的最长路径经过的连接数称为这个节点的高度。树的高度以这个树根节点的高度来表示。只有一个结点的树的高度为0,没有结点的空树的高度为-1.
二叉树
二叉树是一种特殊的树形结构,其树上的每个节点最多只允许拥有两个子节点。每个非叶节点都拥有两个子节点的二叉树称为完全二叉树,完全二叉树具有如下性质,这些性质代表了二叉树的上限:
- 在第\(i\)层的(最大)节点个数:\(2^i\)
- 在高度\(h\)的(最大)节点个数:\(2^h-1\)
- 具有\(n\)个节点的树的最小高度:\(log_2n\)(向下取整),最大高度\(n-1\)
了解这些性质的原因是因为对树的许多操作都和树的高度密切相关,换言之时间复杂度一般为\(O(h)\).
高度越大,对树进行操作的代价就越高,因此希望二叉树的高度尽可能比较小。将树上某个节点的高度差定义为这个节点的左边子树的高度与右边子树的高度的差:
\[diff(x)=|height(leftsubtree(x))-height(rightsubtree(x))\]
高度差越小说明两边的子树的形状越接近,说明在节点数固定的情况下这个树的高度越小。如果树中每个节点的高度差都不超过1,那么称这个树是平衡的。树越平衡越有利于进行搜索。
二叉树的实现
二叉树有两种方法进行实现,第一种是动态的创建结点,再用链表连在一起,这种情况下每个节点的指针域应当包含对其左右节点地址的引用:
1
2
3
4
5struct Node{
int data;
Node* left;
Node* right;
}
第二种方法是用数组进行实现,这种方法常见于存储完全二叉树中,也就是按照从上到下,每一层从左到右,广度优先的方法对树的每一个节点进行编号,再按照编号顺序存储到数组中,在这种情况下,对于编号为\(i\)的节点,其左节点的索引为\(2i+1\),右节点的缩影为\(2i+2\)。
二叉搜索树
二叉搜索树是一种更便于遍历和搜索的特殊二叉树。我们已经知道,当采用线性搜索时,对数组和链表的搜索的时间复杂度为\(O(n)\),但是如果采用二分法查找,则每次只需要遍历当前遍历的节点的一半的节点数,其时间复杂度为\(O(log_2n)\)。利用这个二分法的思想,在二叉树中令任何节点其右子树上的所有节点的值都比其大,其左子树上所有节点的值都比其小或者相等,如此对二叉搜索树进行搜索和增删的时间复杂度都是\(O(log_2n)\)。
二叉搜索树的接口
创建
创建一个二叉搜索树的操作如下:
1
2
3
4
5
6
7
8
9
10
11
12#include <iostream>
using namespace std;
struct BstNode{
int data;
BstNode* left;
BstNode* right;
};
int main(){
BstNode* root;
root = NULL; // 创建了一个空树
}
添加
设计一个函数Inset来添加节点:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22BstNode* GetNewNode(int data)
{
BstNode* newNode = new BstNode;
newNode.data=data;
newNode.left = NULL;
newNode.right = NULL;
return newNode; // 创建了一个新的节点
}
BstNode* Insert(BstNode* root,int data)
{
if(root == NULL) //如果现在的树是空树
{
root = GetNewNode(data);
}else if(data<=root.data) //如果这个输入的树小于等于节点的值,那么应该放在左子树
{
root.left = Insert(root.left,data);
}else{ //如果这个输入的树大于节点的值,那么应该放在右子树
root.right = Insert(root.right,data);
}
return root;
}Insert函数有几点需要注意:
Insert函数中的* root应该是一个全局变量,或者设置输入为指针的指针,才能保持Insert中调整的root和主程序中递归处理的子树是同一个子树
root.left和root.right这里使用了递归
主程序如下:
1
2
3
4
5
6
7
8
9
10int main()
{
BstNode* root = NULL;//to store address of root node
root = Insert(root,15);
root = Insert(root,10);
root = Insert(root,20);
root = Insert(root,25);
root = Insert(root,8);
root = Insert(root,12);
}
搜索
设计一个搜索节点的函数:查找节点的过程也是递归的。我们从根节点开始,根据键值的大小决定是向左子树还是右子树查找。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15bool Search(BstNode* root,int data)
{
if(root == NULL){ // 考虑边界条件:如果根节点为空(代表此时搜索到了叶节点之下或者本来就是空树)
return false;
}
else if(data==root.data) //找到了
{
return true;
}else if(data<root.data)//如果现在的节点的值大于要找的值
{
return Search(root.left,data); //递归搜索左子树
}else{//如果现在的节点的值小于等于要找的值
return Search(root.right,data); //递归搜索右子树
}
}
找到二叉搜索树中的最大值和最小值
不断让临时结点向左或向右走就行。
用迭代实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21int FindMin(BstNode* root){
if(root==NULL){
cout<<"tree is empty";
return -1;
}
while(root.left!=NULL){
root=root.left;
}
return root.data;
}
int FindMax(BstNode* root){
if(root==NULL){
cout<<"tree is empty";
return -1;
}
while(root.right!=NULL){
root=root.right;
}
return root.data;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19int FindMin(BstNode* root){
if(root==NULL){
cout<<"tree is empty";
return -1;
}else if(root.left==NULL){
return root.data;
}
return FindMin(root.left);
}
int FindMax(BstNode* root){
if(root==NULL){
cout<<"tree is empty";
return -1;
}else if(root.right==NULL){
return root.data;
}
return FindMax(root.right);
}
找树的高度
二叉树的高度即左子树和右子树高度中的较大值,可用递归求解。
1
2
3
4
5
6
7
8SearchHeight(root){
leftHeight = SearchHeight(root.left) //向左边遍历到最深
rightHeight = SearchHeight(root.right) //向右遍历到最深
return max(leftHeight,rightHeight)+1;
if (root == NULL){
return -1 //这里需要注意的是,对于单节点树其高度应该为0,+1后变为0
}
}
内存中的操作
系统分配给一个程序的内存,在经典的架构中可以被分为四部分,如下图所示:
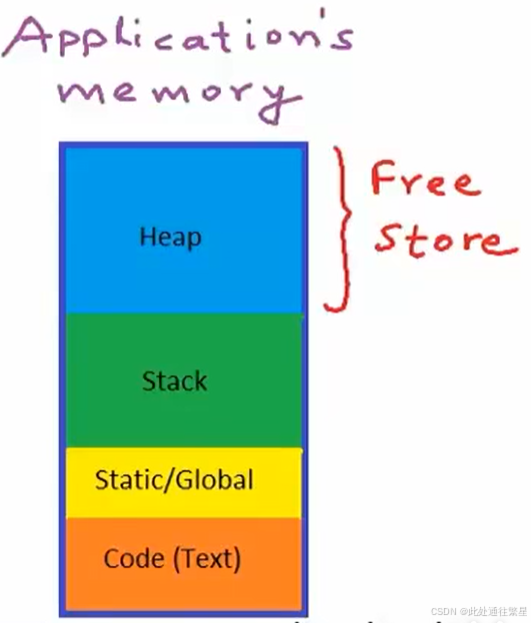
- 代码区:用来存放程序的指令
- 全局区:用于存放全局变量和静态变量以及常量
- 栈区: 暂存空间,用来执行函数,暂存所有的局部变量和函数参数以及函数调用后返回的地址
- 堆区: 自由储存空间,由程序员来进行分配,灵活性大,但其分配的速度较慢,地址不连续,容易碎片化
对于一个如下的调用递归的程序,运行时栈和堆的变化如下:
1 | |
| 1 | 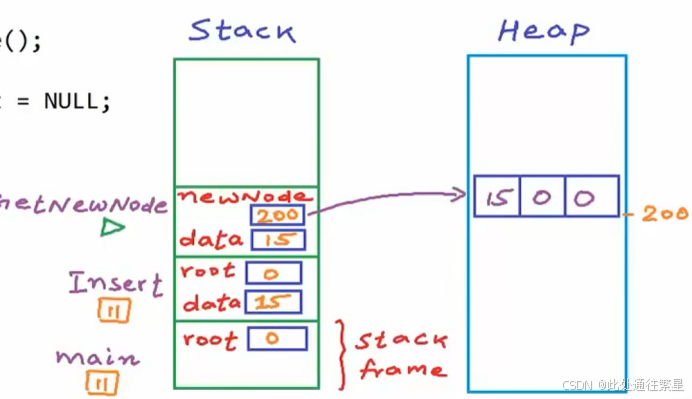 |
程序首先进入main函数,栈中开辟出一部分空间给main函数,程序运行到第一行创建一个root指针指向NULL,运行到第二行main函数运行暂停,程序进入Insert函数,分配栈帧(栈的一片)给insert函数,在insert函数中因为root是空的,所以程序进入GetNewNode函数,分配栈帧给GetNewNode函数,Insert函数停止运行,在堆中创建一个新的节点,栈中创建一个newNode指针指向这个节点,并给节点赋值. |
| 2 | 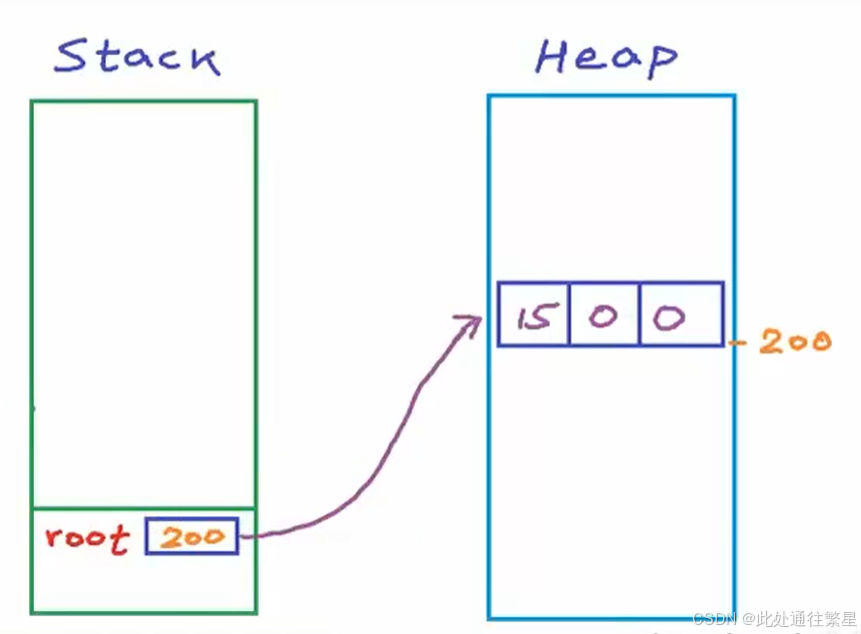 |
GetNewNode函数结束,分配给它的栈帧将会被收回,将root指针返回给Insert函数,继续运行Insert函数: root指向节点,Insert函数运行结束,栈帧收回,返回root指针,此时main函数中root指针指向节点。 |
| 3 | 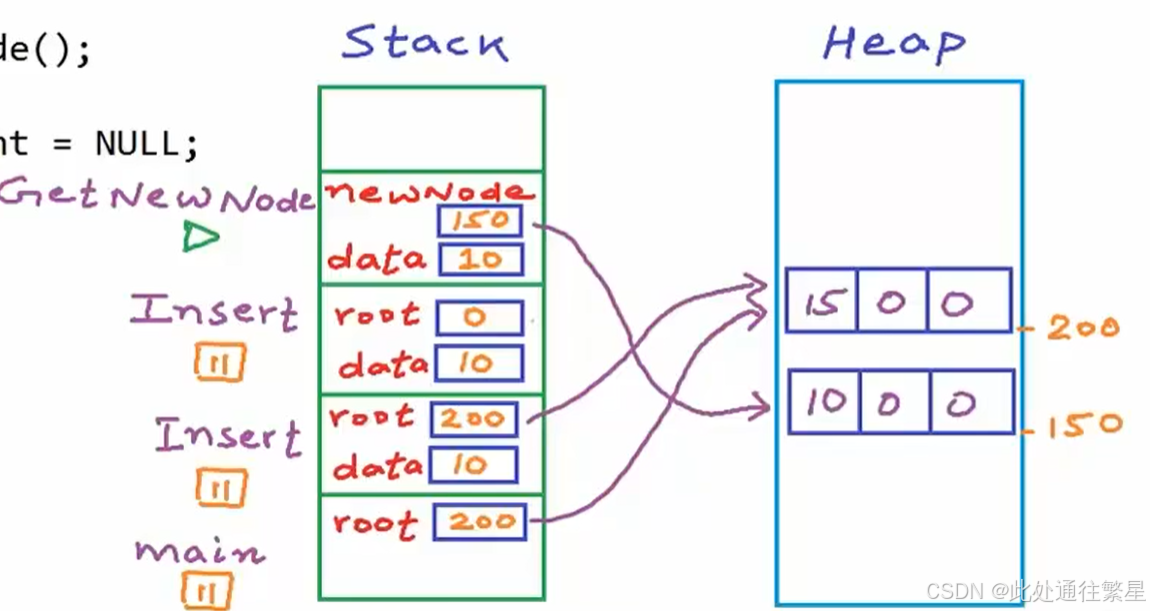 |
程序继续执行下一行,main函数暂停,分配给Insert函数所需的栈帧,root不为空,比较数据的大小,然后进行函数递归,对于递归函数的栈帧分配和普通函数是相同的;root左节点再插入一个节点,新的root为空,再进入GetNewNode函数创建一个新的节点,返回节点的指针。 |
| 4 | 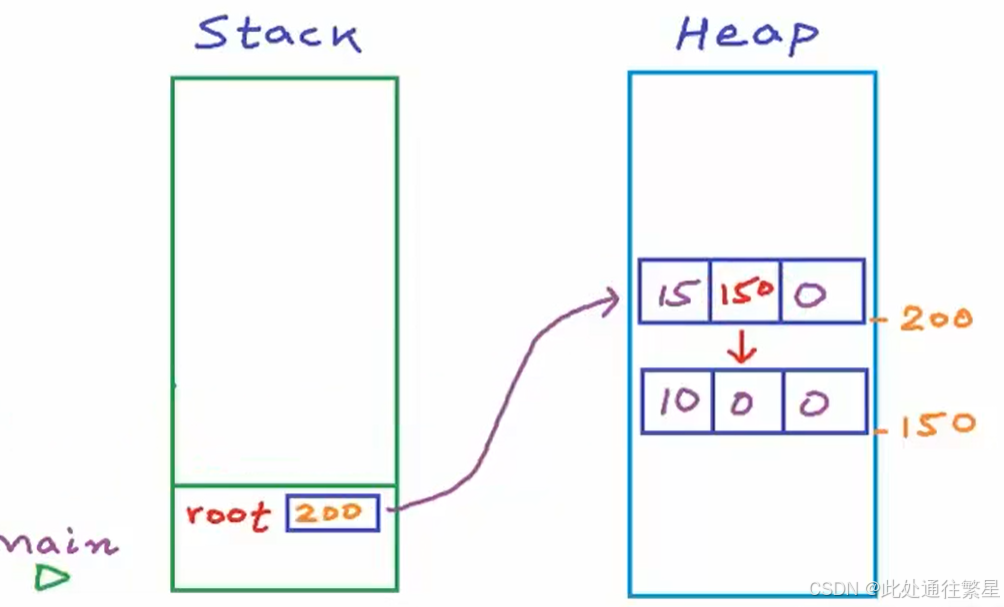 |
GetNewNode函数栈帧被收回,继续执行Insert,root指向新节点,Insert函数暂停,返回到第一层Insert函数,root地址返回给root.left,root.left指向新节点,也就是root指向的地址为200节点的左孩节点地址为150,因此这两个节点连接起来了,最后Insert函数结束,控制返回到main这一行,此时二叉树成功插入两个节点。接下来程序执行过程和上面类似,就不再模拟演示了。 |
| … | … | … |
树的遍历
树的遍历是将树的每个节点都访问一次的过程。树的遍历有两种方法:
- 广度优先
先遍历同一层的全部节点,再访问下一层的节点,广度优先遍历只有一种策略,称为层次遍历。
- 深度优先
先访问一个结点的全部子节点,再访问其孙节点。深度优先算法的遍历可以遵循不同顺序访问根节点、根节点的左子树和右子树:
前序遍历:<root><left><right>
中序遍历:<left><root><right>
后序遍历:<left><right><root>
层次遍历
层次遍历算法的一个难点是为了不走回头路(每个节点只访问一次)。解决这个问题的办法是使用一个列表,在访问一个结点的时候将其子节点放入一个列表中,以便之后访问,当子节点被访问的时候弹出列表。可以发现这个列表遵循的是先进先出的原则,因此此处使用队列。下图展示了一个例子:
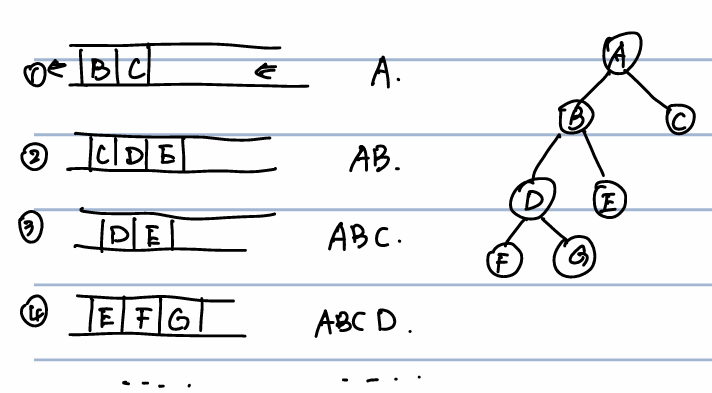
1 | |
上面的操作的时间复杂度是\(O(n)\),空间复杂度而言,最大使用数量取决于子节点:最好的情况下\(O(1)\),最坏的情况(完全二叉树)下,也是平均情况下空间复杂度为\(O(n)\)。
深度优先算法
深度优先算法的思想同样也是使用递归的方式来遍历子树:对于现在访问的树上的一个结点,都按照前序/中序/后序的方法遍历。
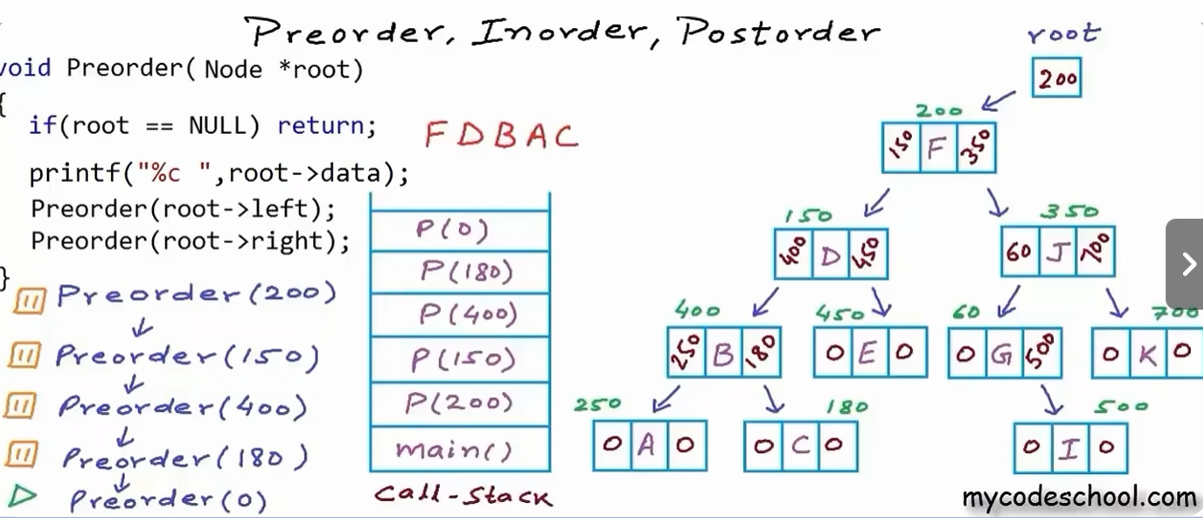
伪代码如下:
1
2
3
4
5
6void Preorder(Node * root){
if (root == NULL) return;
print('%C', root.data);
Preorder(root.left);
Preorder(root.right);
}
1
2
3
4
5
6void Inorder(Node *root){
if(root == NULL) return;
Inorder(root.left);
printf("%c",root.data);
Inorder(root.right);
}1
2
3
4
5
6void Postorder(Node *root){
if(root == NULL) return;
Postorder(root.left);
printf("%c",root.data);
Postorder(root.right);
}printf("%c",root.data);,时间复杂度\(O(n)\),空间复杂度\(O(h)\)
遍历的操作
判断一棵树是否为二叉搜索树
判断一棵树是否为二叉搜索树的基本思想是,二叉搜索树可以看成两个部分:左子树和右子树,对于左子树只要判断其下方的左右子树是否都小于正在遍历的节点值;对右子树同理。然后递归的判断每一个节点的左子树和右子树即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31bool IsSubtreeLesser(Node* root, int value);
bool IsSubtreeGreater(Node* root, int value);
bool IsBinarySearchTree(Node* root);
bool IsBinarySearchTree(Node* root){
if (root==NULL) return true;
if (IsSubtreeGreater(root.right,root.data) && IsSubtreeLesser(root.left,root.data)
&& IsBinarySearchTree(root.left) && IsBinarySearchTree(root.right)){
// 是二叉搜索树的条件:左子树比root大,右子树比root小,左右子树都是二叉搜索树
return true;
}
else
return false;
}
bool IsSubtreeLesser(Node *root,int value){
if(root == NULL) return true;
if(root.data <= value && IsSubtreeLesser(root.left,value)&&IsSubtreeLesser(root.right,value)){
return true;
}
else
return false;
}
bool IsSubtreeGreater(Node *root,int value){
if(root == NULL) return true;
if(root.data > value && IsSubtreeGreater(root.left,value)&&IsSubtreeGreater(root.right,value)){
return true;
}
else
return false;
}
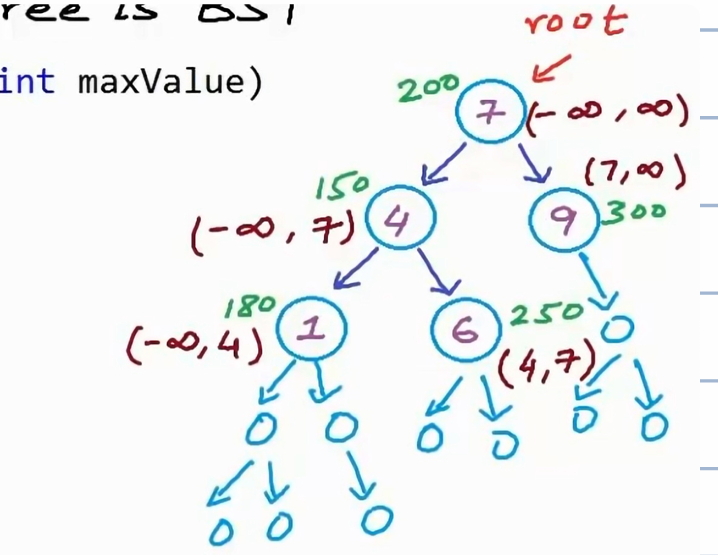
1 | |
但是很多时候使用者可能不希望传入int minValue和int maxValue这两个参数,解决方法是新建一个工具函数:
1
2
3
4
5
6
7
8
9
10
11bool IsBstUtil(Node* root, int minValue, int maxValue){
if (root == NULL) return true;
if(IsBstUtil(root.right,root.data,maxValue) && IsBstUtil(root.left,minValue,root.data)
&& root.data > minValue && root.data< maxValue)
return true;
else
return false;
}
bool IsBinarySearchTree(Node* root){
return IsBstUtil(root,INT_MAX,INT_MIN); //初始边界应该为正无穷到负无穷
}
从二叉搜索树中删除一个结点
从二叉搜索树中删除一个结点的话需要进行讨论:
- 对于叶节点,也就是没有子节点的节点,直接删除就好
- 对于非叶节点,我们希望在删除之后依然想要保留剩下的子节点:
- 只有一个子节点时:删除某个节点之后直接将其子节点依附到删除节点的位置就好
- 当被删除的节点有两个子节点时,希望将处理情形退化到只有一个子节点的情况,处理方法是用这个节点子树中的某个节点的值先替换这个节点,然后再删除刚才使用的那个节点的值的位置,此时希望将删除节点的操作退化到只有一个子节点时的操作:那么在子树中,有下面两种节点只有一个子节点:
- 右子树的最小值节点
- 左子树的最大值节点
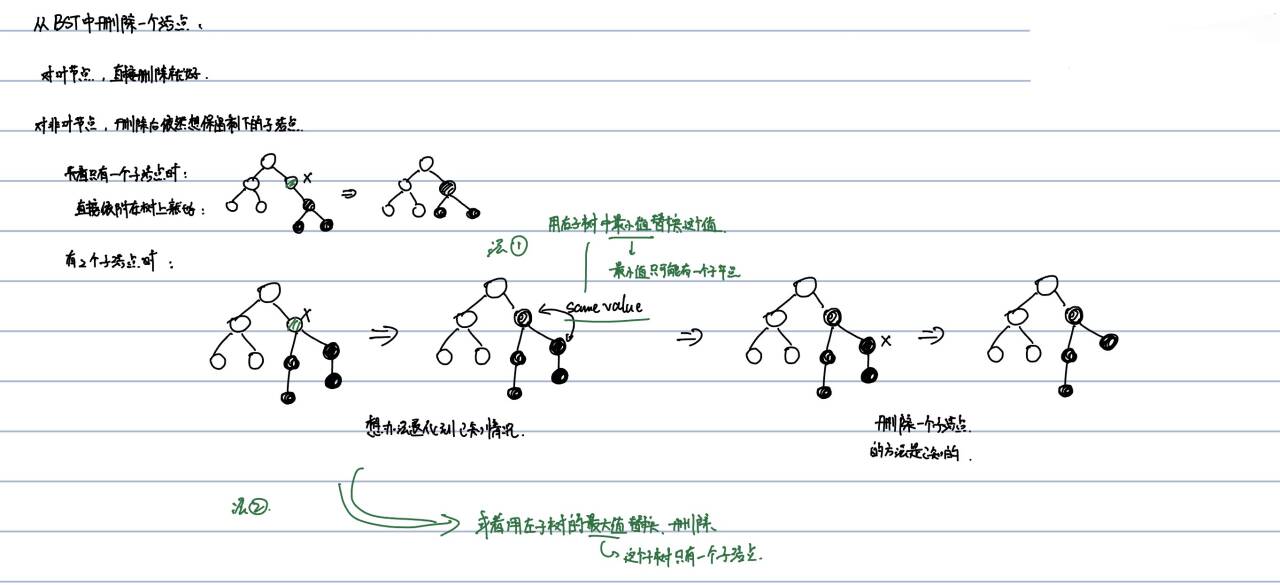
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40//Function to find minimum in a tree.
Node* FindMin(Node* root)
{
while(root.left != NULL) root = root.left;
return root;
}
// Function to search a delete a value from tree.
struct Node* Delete(struct Node *root, int data) {
if(root == NULL) return root; //返回改变后的根节点
// 删除点在左/右子树,将问题降级为从左/右子树中删除
else if(data < root.data) root.left = Delete(root.left,data);
else if (data > root.data) root.right = Delete(root.right,data);
// Wohoo... I found you, Get ready to be deleted
else {
// Case 1: No child
if(root.left == NULL && root.right == NULL) {
delete root;
root = NULL;
}
//Case 2: One child
else if(root.left == NULL) {
struct Node *temp = root;
root = root.right; //用右子节点作为这个节点
delete temp;
}
else if(root.right == NULL) {
struct Node *temp = root;
root = root.left; //用左子节点作为这个节点
delete temp;
}
// case 3: 2 children
else {
struct Node *temp = FindMin(root.right); //用右子树的最小节点替代被删除的节点
root.data = temp.data;
root.right = Delete(root.right,temp.data); // 在右子树中删除这个最小值节点
}
}
return root;
}
找中序遍历的后继
中序遍历的过程是遍历左子树,再输出根节点,再遍历右子树。在遍历的过程中,如果称一个节点的所有子节点都被访问过才算被访问,如此访问过的结点顺序构成一个数列,这个数列的某个元素的后一项代表了下一个被完全遍历的节点,称为这个节点的后继,一个例子如下图所示:
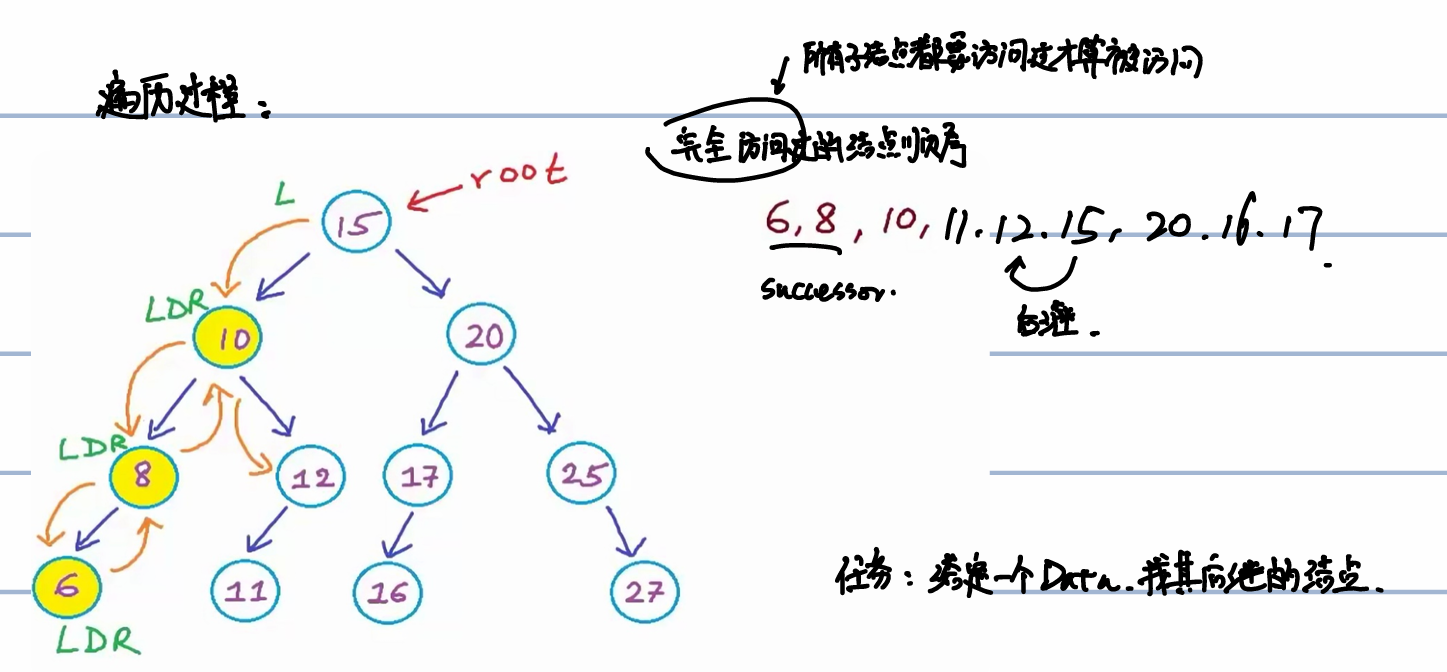
现在的任务是给定一个节点,要找到这个节点在中序遍历中的后继节点。
这个任务可以分割成两个情况:
- 节点有右子树,那么后继为右子树的最左边的节点(即最小值节点)
- 节点没有右子树,那么后继为这个节点上方未访问过的第一个父节点,找父节点有两个方法:
- 在
Node结构中添加一个指向父节点的指针,从当前节点向上查找,直到遇到一个节点是其父节点的左子树。 - 从根节点出发,寻找目标节点的路径,在路径中记录最后一个将目标节点包含在其左子树中的祖先节点,这个节点就是中序后继。
如此的时间复杂度为\(O(h)\),取决于树的深度。
- 在
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19struct Node* Getsuccessor(struct Node* root, int data){
struct Node* current = Find(root,data);
if (current == NULL) return NULL;
if (current.right !NULL){ //第一种情况
return FindMin(current.right);
}
else{
struct Node* successor = NULL;
struct Node* ancestor = root;
while(ancestor != current){
if (current.data < ancestor.data){
successor = ancestor; //目前找到的左子树中current为这个左子树最深的节点
ancestor = ancestor.left;
}
else
ancestor = ancestor.right;
}
}
}
图
图是一种节点和连接的集合。图的基本单元是顶点和边:顶点即节点,数学上表示为:
\[G=(V,E)\] \(V\)是顶点集,\(E\)是边集。
边是两个顶点的连接,一条边以边相连接的两个顶点定义,边可以有方向也可以没有方向,可以有权重也可以没有权重。
现实中的图可以用来表示网络的拓扑结构、网站的相互链接关系、社交网络等等。
图的基本属性
在介绍图的基本属性之前先要介绍图的两种特殊情况:
- 自环:边的连接的两个顶点是同一个顶点
- 多重边:两个相同的顶点间有多个边
在没有上述这两种特殊条件的图中:
对于有向图,边的数量\(|E|\)在\([0,n(n-1)]\)之间;对于无向图,边的数量\(|E|\)在\([0,\frac{n(n-1)}{2}]\)之间.
如果边的数量\(|E|\)接近最大值,那么称这个图是稠密图,稠密图一般用后面提到的邻接矩阵存储;如果边的数量\(|E|\)接近最小值,那么称这个图是稀疏图,稠密图一般用后面提到的邻接表存储;
术语
- Path: 一组相连的边的有序序列
- Simple Path:没有重复路径的path
- walk:可以有重复路径的path
- closed walk:路径的起止顶点相同
- 环:一个闭合的simple walk
- 强连接图:从任意顶点到任意其他顶点都有path
- 单向图:没有环的有向图
图的存储
边列表
我们可以用两个列表来存储一个图所有的信息:
- vertex list:用一个列表存放所有顶点
- edge list:用一个列表存放所有的边
这里定义边:
当边有权重的情况下可以在加一个域用于存放数据。1
2
3
4
5
6class Edge{
char *startVertex;
char *endVertex;
}
string_vertex_list[MAX_SIZE];
Edge edge_list[MAX_SIZE];
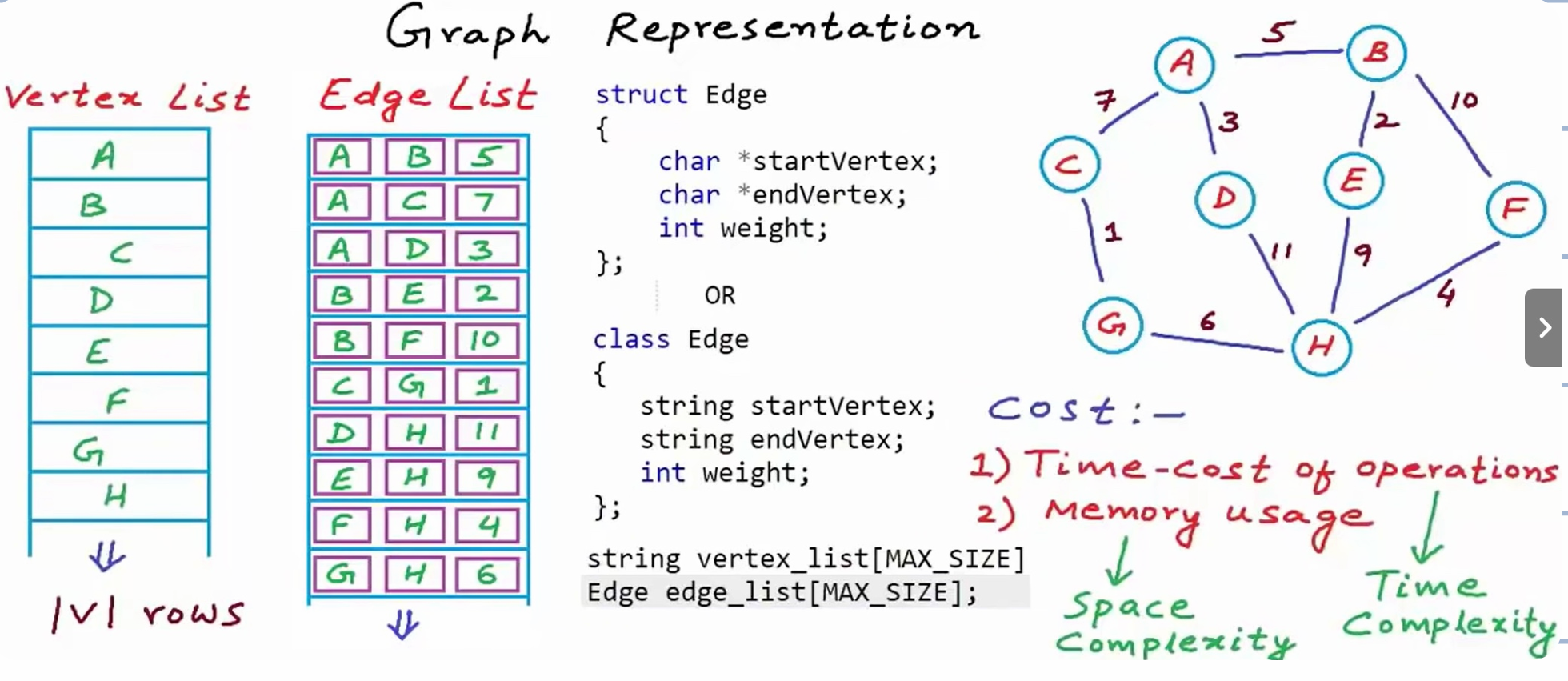
但是上述方法的成本比较高:
- 空间复杂度
对vertex list:\(O(|V|)\);对edge list,直接使用节点的索引值以节约存储空间:\(O(|E|)\);
整个的空间复杂度:\(O(|V|)+O(|E|)\)
- 时间复杂度
图中最花费时间的操作有两个:找到一个结点的所有相邻接点和找到两个节点是否相连,由于都需要遍历列表edge list,在线性遍历下,时间复杂度为:\(O(|E|)\)
但是对于图而言,边的数量几乎随着顶点的数量指数上升\(O(|E|)→O(|V|^2)\)。
邻接矩阵
为了改进边列表的时间复杂度,设置一个\(|V|×|V|\)的矩阵\(A\)来表示顶点索引,当图为无权重时:
\[
A_{i,j}=\begin{cases}
1 \text{, if ∃ }E \text{ from }i \text{ to }j\\
0,\text{otherwise}
\end{cases}
\]
在无向图中,这个矩阵应当是一个对称矩阵。
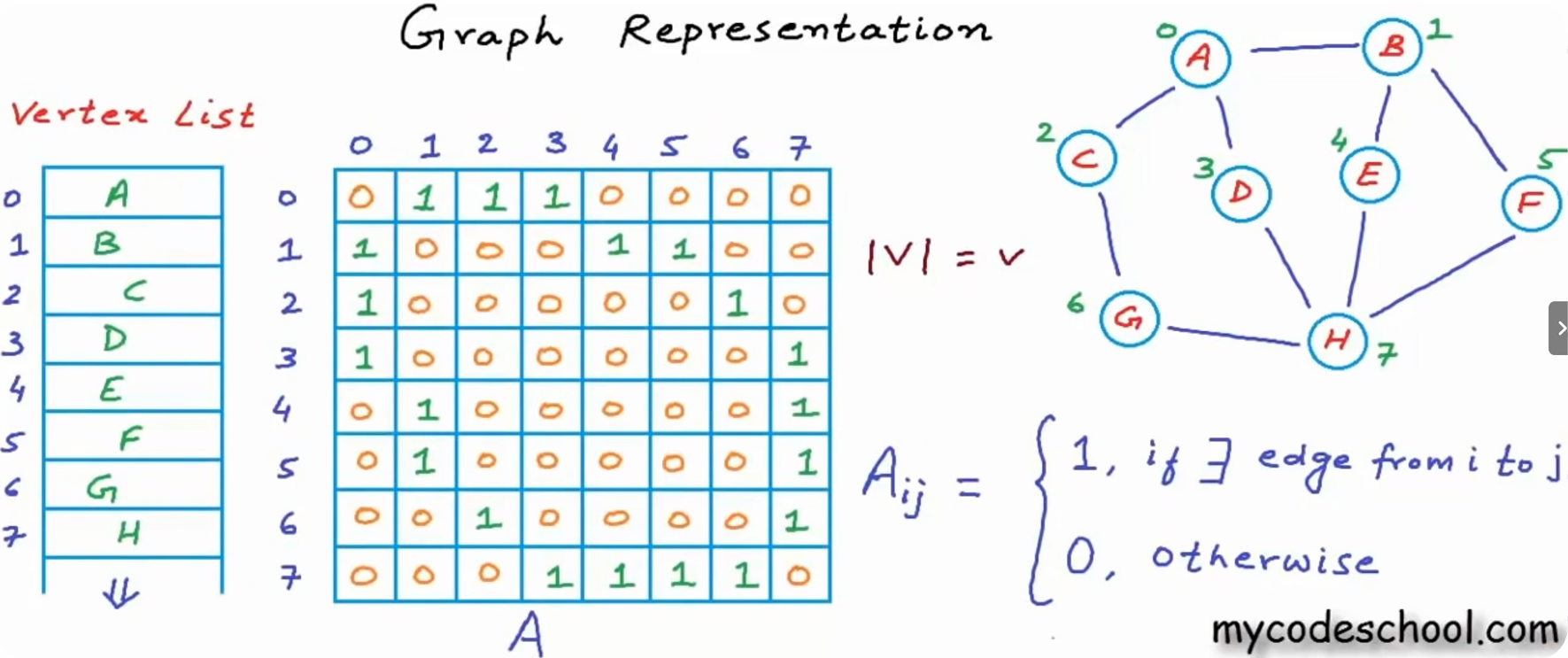
在A中找某个节点的相邻接点的过程:
- 首先在vertex list找节点,这一步的时间复杂度为常数\(O(1)\)
- 在邻接矩阵中找对应行的哪些列为1\(O(|V|)\)
找两个节点是否相连的时间复杂度为:\(O(1)+O(|V|)=O(|V|)\),其中邻接矩阵可以用哈希表进一步减少到\(O(1)\),因此总的时间复杂度最少可以减小到\(O(1)\)。
不过这个方法的内存使用为\(O(|V|^2)\):如果对稀疏图使用这种方法的话会有大量的元素值为“0”,导致存储空间的浪费。
对于有权图,矩阵中的每一个元素设置为对应边的权重值。
邻接表
对于邻接矩阵的一行,这一行不仅存放了哪些节点与某个节点相连,也存储了这个节点没有与那些节点相连。如果后一个部分可以不用存储的话,那么直接可以用一个列表保存某个节点与节点相连:比如如果一个顶点\(A\)与\(B,C,D\)相连,那么可以将\(A\)存储为\(\{B,C,D\}\).
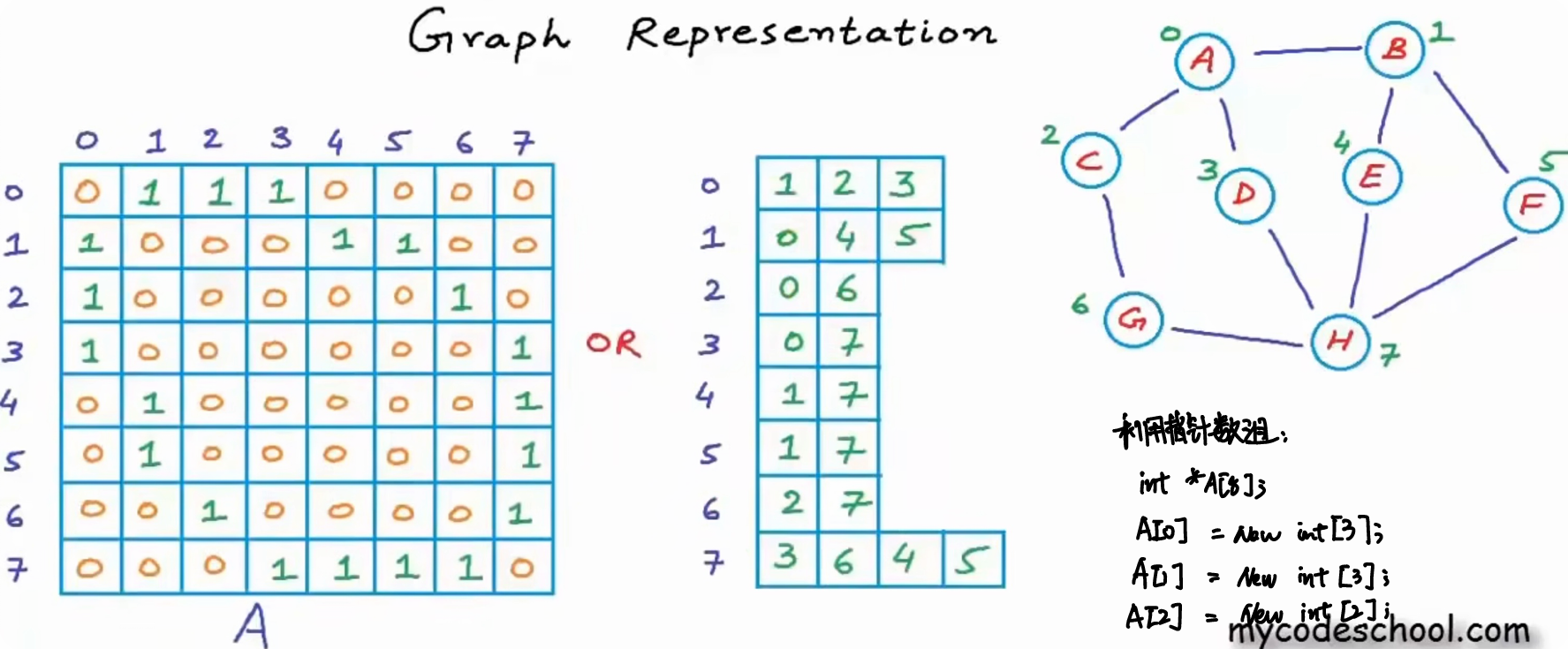
在这种情况下利用可以利用一个指针数组存储这个表,比如:
1
2
3
4int *A[8];
A[0] = new int[3];
A[1] = new int[3];
A[2] = new int[2];
对时间复杂度,
- 找到两个结点是否相连,在最差的情况下,时间复杂度为\(O(|V|)\)(线性搜索),\(O(log_2|V|)\)(二分搜索)
- 找到一个结点的相邻结点,在最差的情况下,时间复杂度为\(O(|V|)\)(线性搜索),\(O(log_2|V|)\)(二分搜索)
在边的数量小于顶点平方的情况下,这种操作的空间复杂度更小。
但是在这种情况下,增加图中的边会更加困难,因为每一个数组的容量大小是固定的,增加图中的边意味着需要动态扩容数组,因此每个顶点的边邻接表可以使用链表:
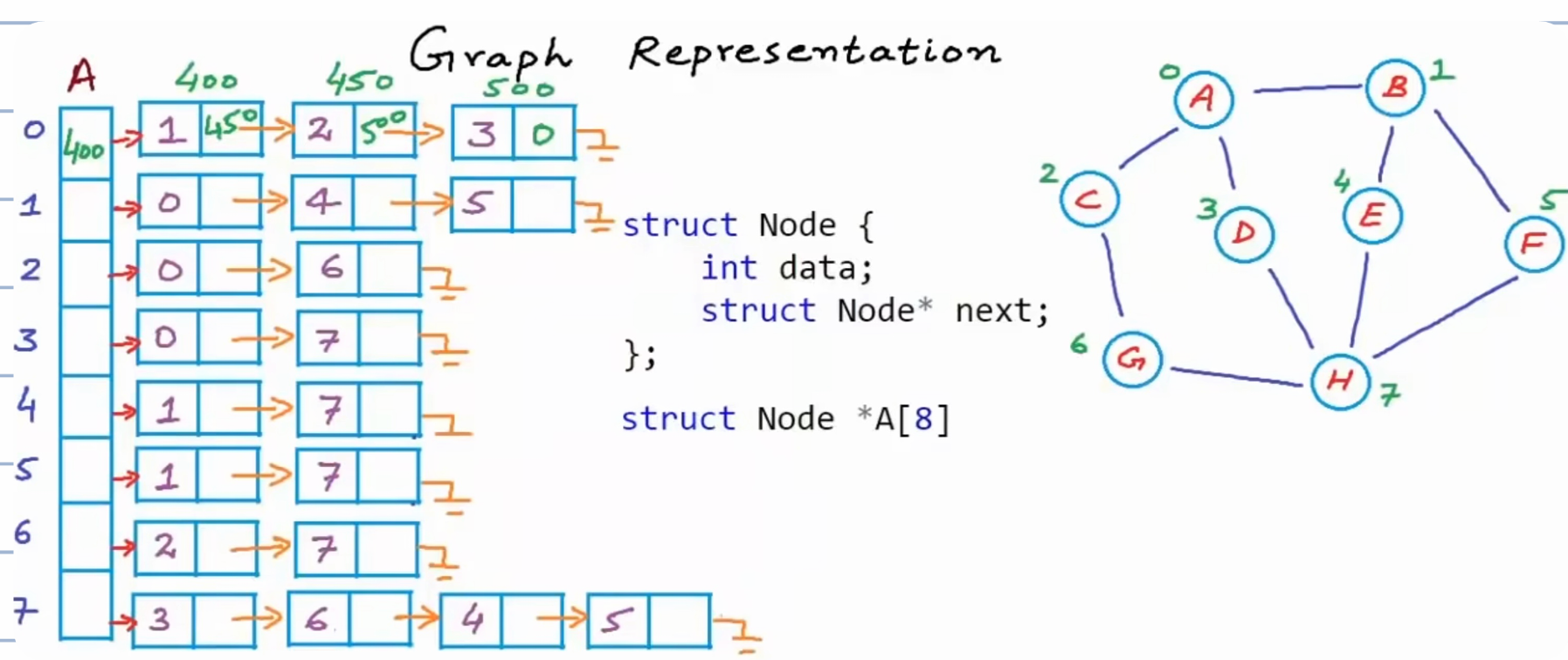
这就是邻接表,邻接表的空间复杂度为\(O(|E|+|V|)\),时间复杂度和之前的分析相同。
利用二叉搜索树来存放还可以进一步减少查找和增删的成本。