天线知识点总结

知识点总结

author: Kigha Oreki/ Hikari Kobayashi （Hikari Kobayashi的博客）

基本理论*

传输线模型

传输线模型中的幅值电压反射系数\(Γ\)： \[Γ=\frac{Z_L-Z_0}{Z_L+Z_0}\] 其中\(Z_L\)为天线负载的阻抗，\(Z_0\)为传输线上的阻抗。
驻波比：
\[SWR=\frac{V_{max}}{V_{min}}\]

麦克斯韦方程组·平面波理论

真空中的特征阻抗：\(η_0=√\frac{μ_0}{ϵ_0}=120π\)
波数：\(k=\frac{2π}{λ}=ω√{μ_0ϵ_0}\)
E和H的关系:\(H=\frac{1}{2η}|E|\)

天线基础知识

天线的方向图

HPBW(Half-Power Beamwidth)： \(U(2θ_{HPBW})=0.707U\)（对应下降3dB）
FNBW(First-Null Beamwidth): \(U(2θ_{FNBW})=0\)

天线的远场区

\[\frac{2D^2}{λ}\]

天线的能量

• 平均能量密度 \[W_(av)=\frac{1}{2}Re[E×H^*]=\frac{1}{2η}|E|^2\]
  
• 平均辐射强度 \[U=r^2W_{av}\]
  
• 平均能量 \[P_{rad}=∯W_{rad}ds=∯UdΩ=∫_0^{2π}∫_0^{π}W_{rad}r^2sinθdθdφ\]

注意积分的上下限，题目没有给出的情况下： \(θ:0-π,φ:0-2π\)

• 方向性 \[D=\frac{U}{U_0}=\frac{4πU}{P_{rad}}\]

• 有效面积 \[A_{em}=\frac{λ^2}{4π}D_{max}\]

• 辐射阻抗 \[P_{rad}=\frac{1}{2}I^2R_r\]

• 输入阻抗 \[\frac{1}{2}I_{in}^2R_{in}=\frac{1}{2}I^2R_r+P_{waste}\] 当\(P_{waste}=0\)时，对偶极子天线有\(I_{in}=I_0sin(\frac{kl}{2})\)。
  \(R_{in}=\frac{R}{sin^2(\frac{kl}{2})}\)。
  当偶极子天线长度\(l=\frac{λ}{2}\)时，输入转发射的效率最高。

天线的效率

\[e=e_re_{cd}\] \(e_r\)：由传输线模型反射（reflection）所造成的损失产生的效率：\(e_r=1-|Γ|^2=\frac{P_{avg}}{P_{input}}\)
天线的增益： \[G=e_{cd}D\] 考虑传输线模型中的反射：
\[G_{realize}=e_re_{cd}D=(1-|Γ|^2)G\]

天线的极化

单个天线的极化方式：a) 线极化 b) 圆极化 c) 椭圆极化
极化适配：如果波的极化方向\(\hat{ρ_w}\)和天线的极化方向\(\hat{ρ_a}\)不相同，波的接收会有损失，定义极化损失因子（PLF）或极化效率： \[PLF=|cosφ_p|^2\] \(φ_p\)为\(\hat{ρ_w}\)与\(\hat{ρ_a}\)的夹角，如图所示：

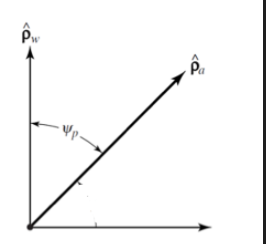
当两天线正交时，理论上接收不到任何电磁波。当两天线重合时，极化效率最高。

天线的互易性*：同一个天线在作为发射或接收天线时所有性质不变。

偶极子天线

辅助位函数

\[A=\frac{μ_0Il}{4πr}e^{-jkr}\hat{e_z}\]

由\(A=\hat{e_r}A_r+\hat{e_θ}A_θ+\hat{e_φ}A_φ\)，有：
\(\begin{cases} A_r=A_zcosθ \\ A_θ=-A_zsinθ \\ A_ϕ=0 \\ \end{cases}\) ### 远场区辐射 由\(H=\frac{1}{μ_0}▿×A\)：
\[H_ϕ=j\frac{Il}{2λr}sinθe^{-jkr}\] 由\(E=\frac{1}{jωɛ}▿×H\)：
\[E_θ=j\frac{60πIl}{λr}sinθe^{-jkr}\]

能量和方向性

\[W=\frac{1}{2}Re[E×H^*]=\frac{1}{2η}|E|^2=\frac{15πI_A^2l^2}{λ^2r^2}sin^2θ\hat{e_r}\]
\[P=∯WdS=40π^2I^2(\frac{l}{λ})^2\]
\[D_0=4π\frac{U_{max}}{P_r}=\frac{3}{2}\]

天线阵列

各向同性天线阵列的参数

各向同性天线阵列如图所示：

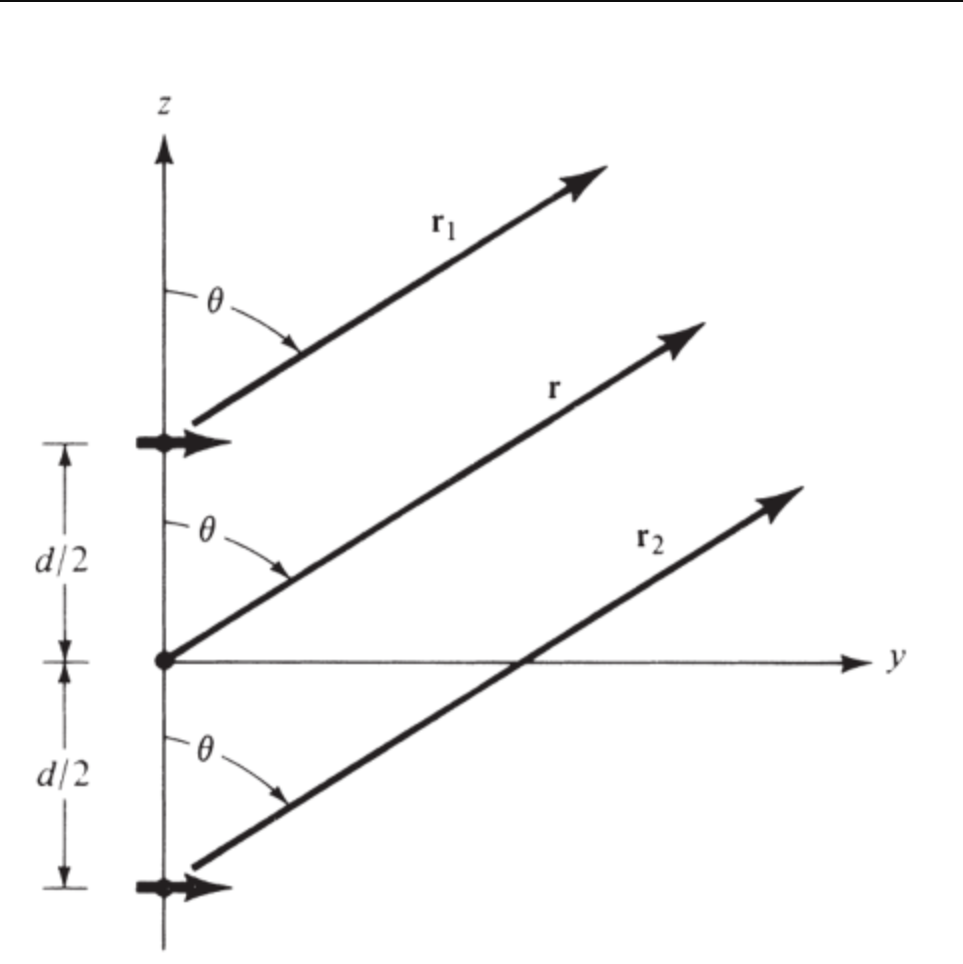
• 阵列因子
  如图，由\(E=∑E_i\):
  \[E=\frac{E_0}{r^2}[C_01+C_1e^{-jkr_1}+...]\] \[AF_{norm}=∑_{n}^NC_ne^{j(n-1)(kdcosθ+β)}\] \[AF_{norm}=\frac{sin(\frac{N}{2}φ)}{sin(\frac{1}{2}φ)}\]

n=0的天线（参考天线）位于原点，如果负半轴有天线，n应当从负数开始加起。

\(d\):两个天线的间距，\(β\):两个天线的相位差(对偶极子天线来说为0)，\(C_n\)为激活常数（默认为1）

• 平均辐射强度（归一化） \[U_{norm}=AF_{norm}^2\]

• 最大方向性 \[D_0=2N(\frac{d}{λ})\]

天线阵列的方向图

方向图的最大点： \(AF(θ)=AF(θ)_{max}\)时的\(θ\)
方向图的零点： \(AF(θ)=0\)时的\(θ\)
方向图的半波宽度： \(AF_{norm}|θ_{3db}=0.707,Θ_{hpbw}=2|θ_{max}-θ_{3dB}|\)

线天线

类型

环形天线

环形天线根据电尺寸分为两类： 电大天线和电小天线。
电大天线的周长近似于波长，电小天线的波长小于0.1个波长。

螺旋天线

• 正常模式（Normal）
  当每一节螺旋的长度\(L_0<<λ\)时，螺旋天线可以视作是偶极子天线和环形天线的组合。
  螺旋天线的轴比：
  \[AR=\frac{|E_θ|}{|E_ϕ|}=\frac{2λs}{(πD)^2}\] \(s\):相邻螺旋的高度差，\(D\):螺旋天线一个螺旋（圆部分）的直径。
  当螺旋天线的轴比为0时，螺旋天线是线极化的。
  正常模式下，整个螺旋线长度上的电流是恒定大小和相位的。由于其尺寸决定了天线的辐射特性，其辐射阻值\(R_r\)非常大，容易造成阻抗不匹配，且带宽很窄，辐射效率低下，方向性也比较差。

• 端射模式（End-fire） 螺旋天线一个螺旋（圆部分）的周长为\(C\)，当\(C≈λ,S≈\frac{λ}{4}\)时，螺旋天线视为端射模式。 端射模式的带宽比较宽，因此端射模式的辐射效率比较高。在端射模式下，天线的方向性非常的好。

八木天线

八木天线的结构和方向图如下图所示：

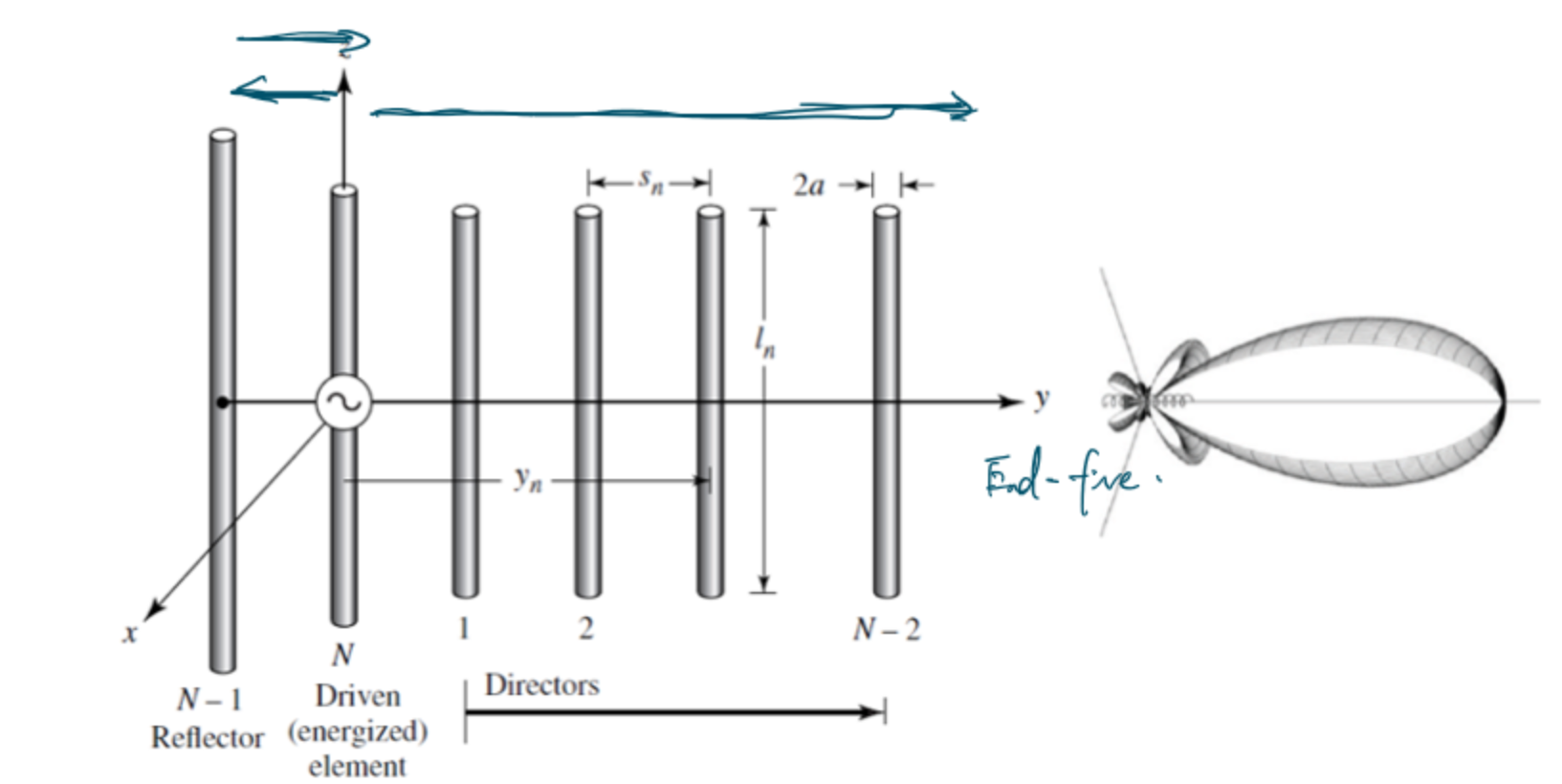
八木天线的结构：
反射子：反射电磁波。
驱动子： 发射电磁波，其长度通常略小于\(0.5λ\)(0.45-0.49)，通常是一个环形天线用于阻抗匹配。
方向子： 通过感性电流扩大辐射，其长度通常略小于\(0.5λ\)（0.4-0.45）。
通常方向子的间距在\(0.3λ-0.4λ\)之间。

非频变天线

概念

非频变天线指电磁波频率对其辐射性质（方向图，前后比，输入阻抗等）变化不大的一类天线。
天线的一系列物理边缘\(r\)可以与一系列频率的电磁波产生谐振。对于非频变天线，如果其第一个边缘\(r\)的表达式为\(r=F(θ,ϕ)\)，当后续边缘的表达式满足：
\[KF(θ,ϕ)=F(θ,ϕ+C)\] 其中K表示为第一个K倍大的电尺寸，C为第二个边缘旋转C角，如此旋转角度C取决于K而不取决于\(θ\)或者是\(ϕ\)，进而实现频率无关。
对其两边求微分后解得\(r=e^{aϕ}f(θ)\)，所有边缘满足该表达式的天线是非频变天线。

类型

• 平面等角螺旋天线(Planar Spiral Antenna)
  
• 锥形等角螺旋天线(Conical Spiral Antenna)
  
• 阿基米德螺旋天线
  
• 对数周期天线

等角螺旋天线

因为等角螺旋的表面几何形状可以用\(f(\theta)\)来表示，所以它可以被设计为一个频率无关天线。
对于等角螺旋天线，取特殊值时，它的半径为：
\[r = \rho = Ae^{a\phi}=\rho_0 e^{a(\phi-\phi_0)}\] 以波长记时，
\[\rho_\lambda = Ae^{a[\phi + \ln(\lambda)/a]}\]

所以，改变\(\lambda\)即改变\(\phi_0\)，结果方向图只是单纯的旋转而其它不变，所以我们得到的时频率无关天线。

螺旋总长的计算式*
\[L=(\rho_1 - \rho_0)\sqrt{1+\frac{1}{a^2}}\] 等角螺旋辐射的波的极化由臂长来控制，全臂长和波长相比很小时，辐射场是线极化的，全臂长与波长相比不断增高时会从椭圆极化最终变成圆极化。实际应用中大多数会选轴比等于或小于\(2:1\)的点，它发生在全臂长约一个波长的时候。

对数周期天线

另一个频率无关的天线时对数周期天线，但是，它的形状不能由角度来描述，所以其实它不是真正的频率无关。
对数周期的结构形状可以写成：
\[\theta = \theta_0 \sin [b\ln(\frac{r}{r_0})]\]

只要角频率的对数相差\(2\pi/b\)，那么\(\theta\)就会重复，所以叫做对数周期天线。
虽然它不是严格频率无关，但是实际应用中把振幅变化设计的很小，所以看成是频率无关的。
最后，对数周期天线是线极化的。

微带天线

辐射原理

当微带天线的贴片宽度\(W\)与基底高度\(h\)之比\(\frac{W}{h}>>1\)，并且\(ɛ_r>>1\)时，磁场从基底溢出（微带天线通过这样的磁场泄漏来发射电磁波），因此微带天线的电尺寸要大于实际尺寸，称之为边界效应。
在计算时，将电池溢出的部分和天线的基底一同视作新的基底，其等效介电常数为\(ɛ_{reff}\)。
\[1<ɛ_{reff}<ɛ_r\]

馈电方式

微带天线有四种馈电方式:
- 微带传输线馈电（Microstrip line feed） - 探针馈电（Probe feed）
- 耦合孔馈电（Aperture-coupled feed）
- 耦合馈电（Proximity-coupled feed）

如下图所示：

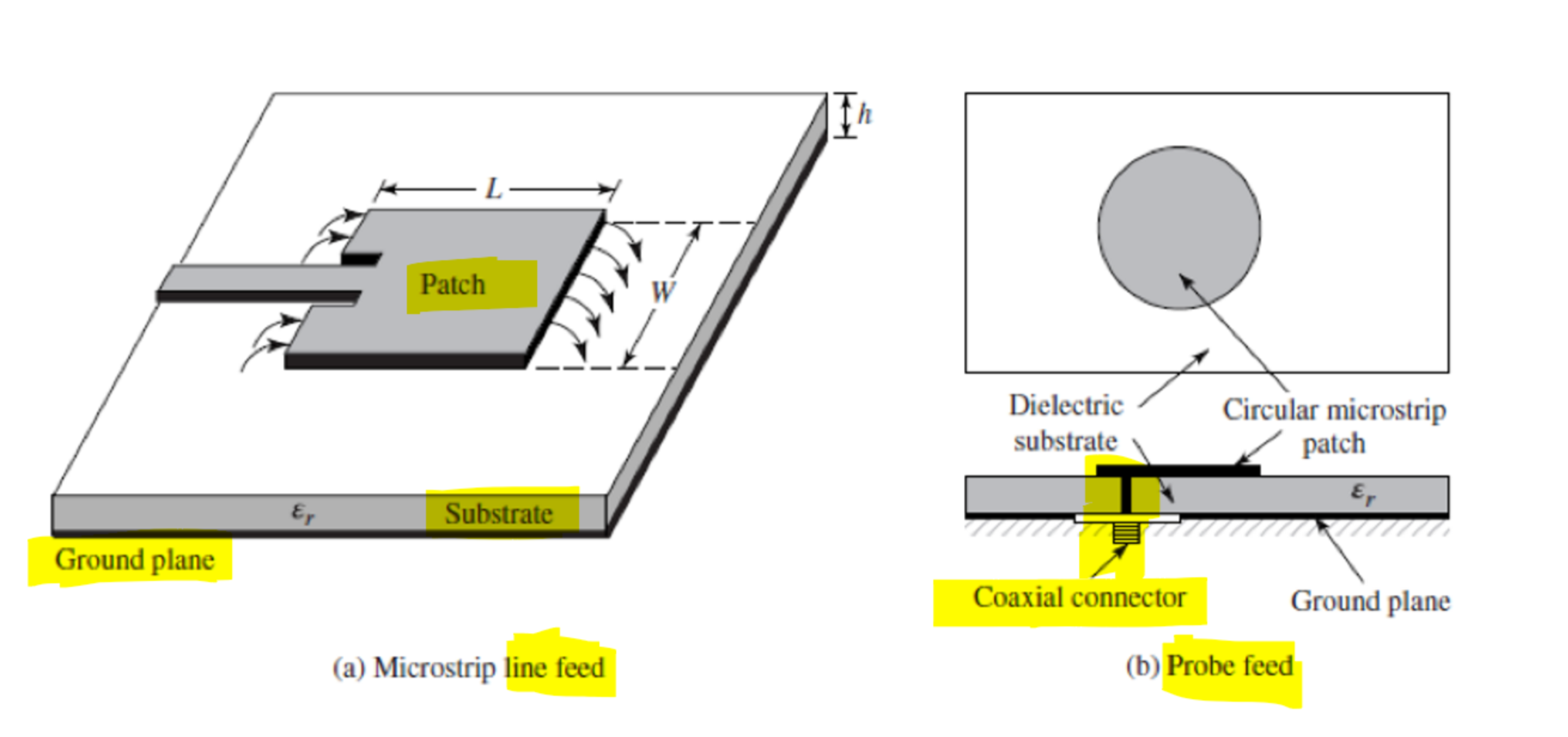
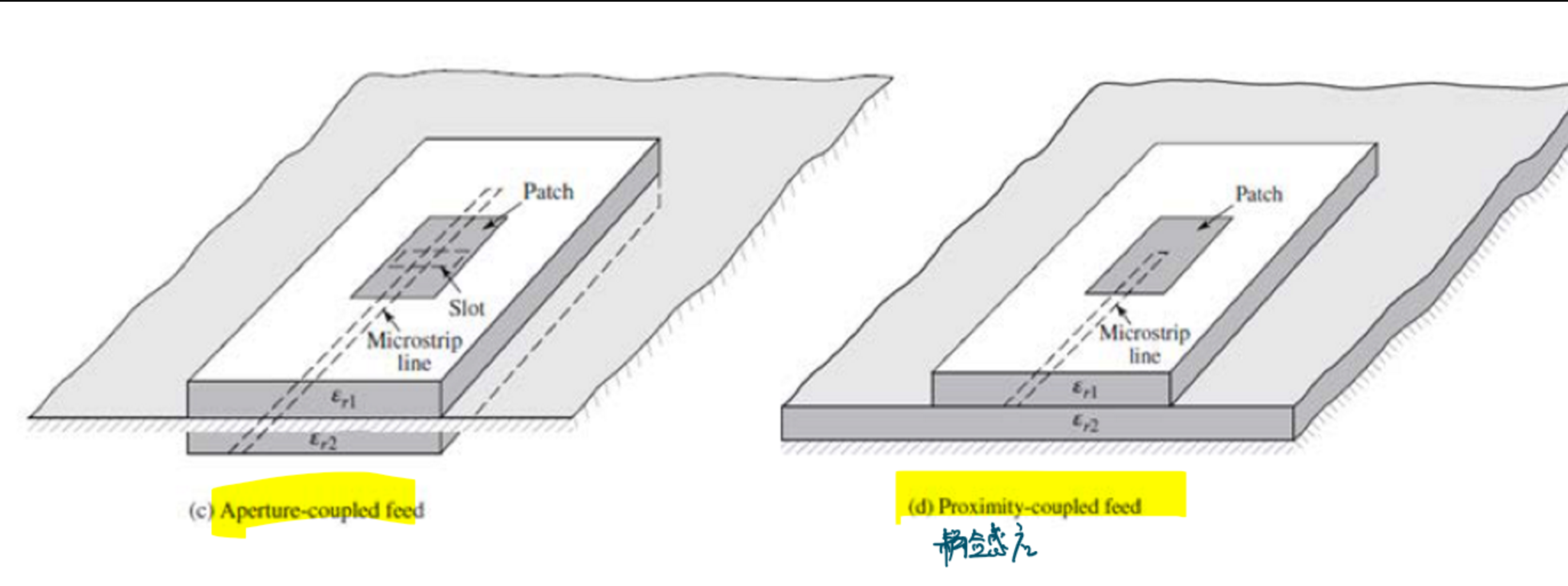
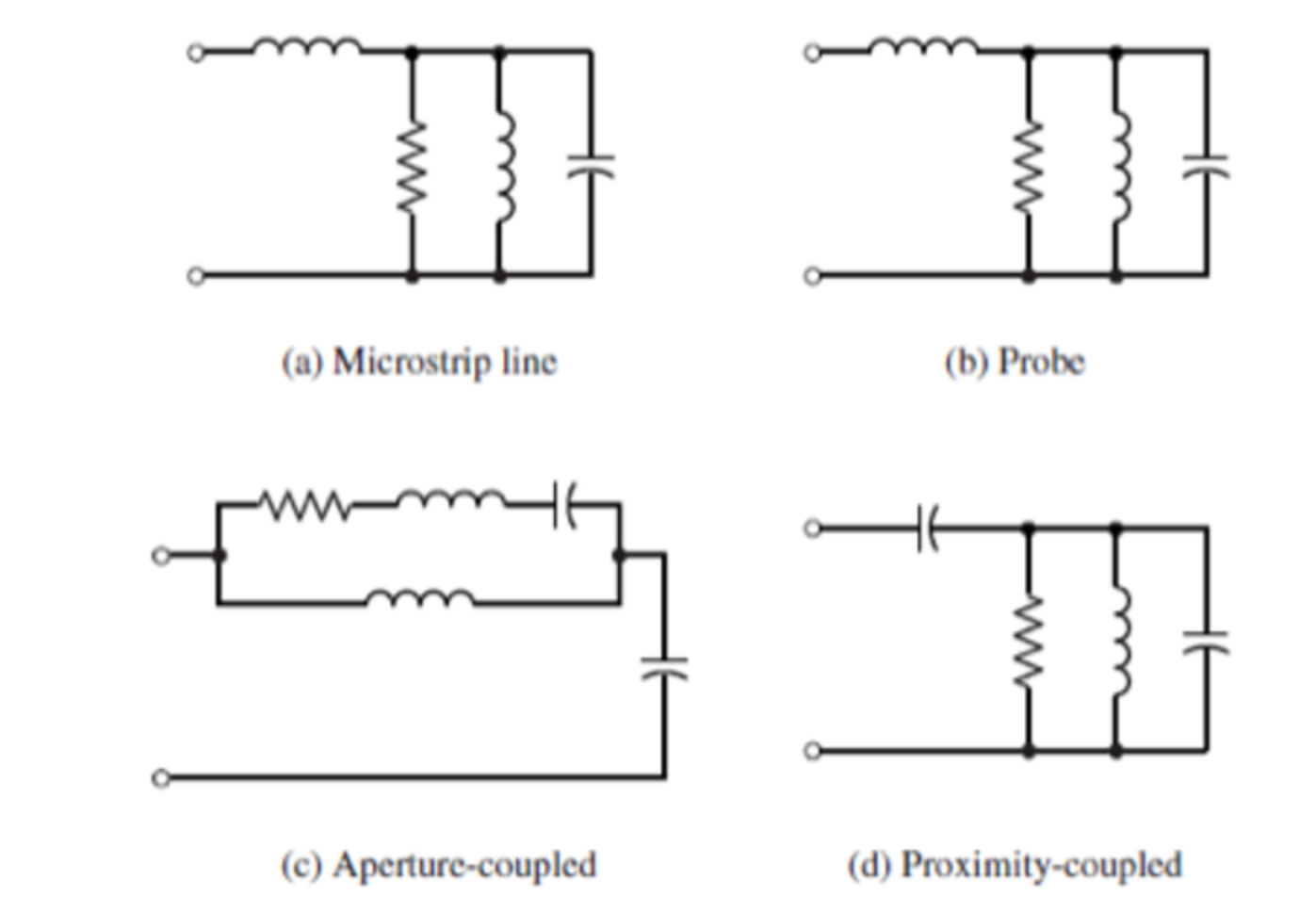
四种馈电方式的等效电路为：

结构

微带天线的结构如下图所示：

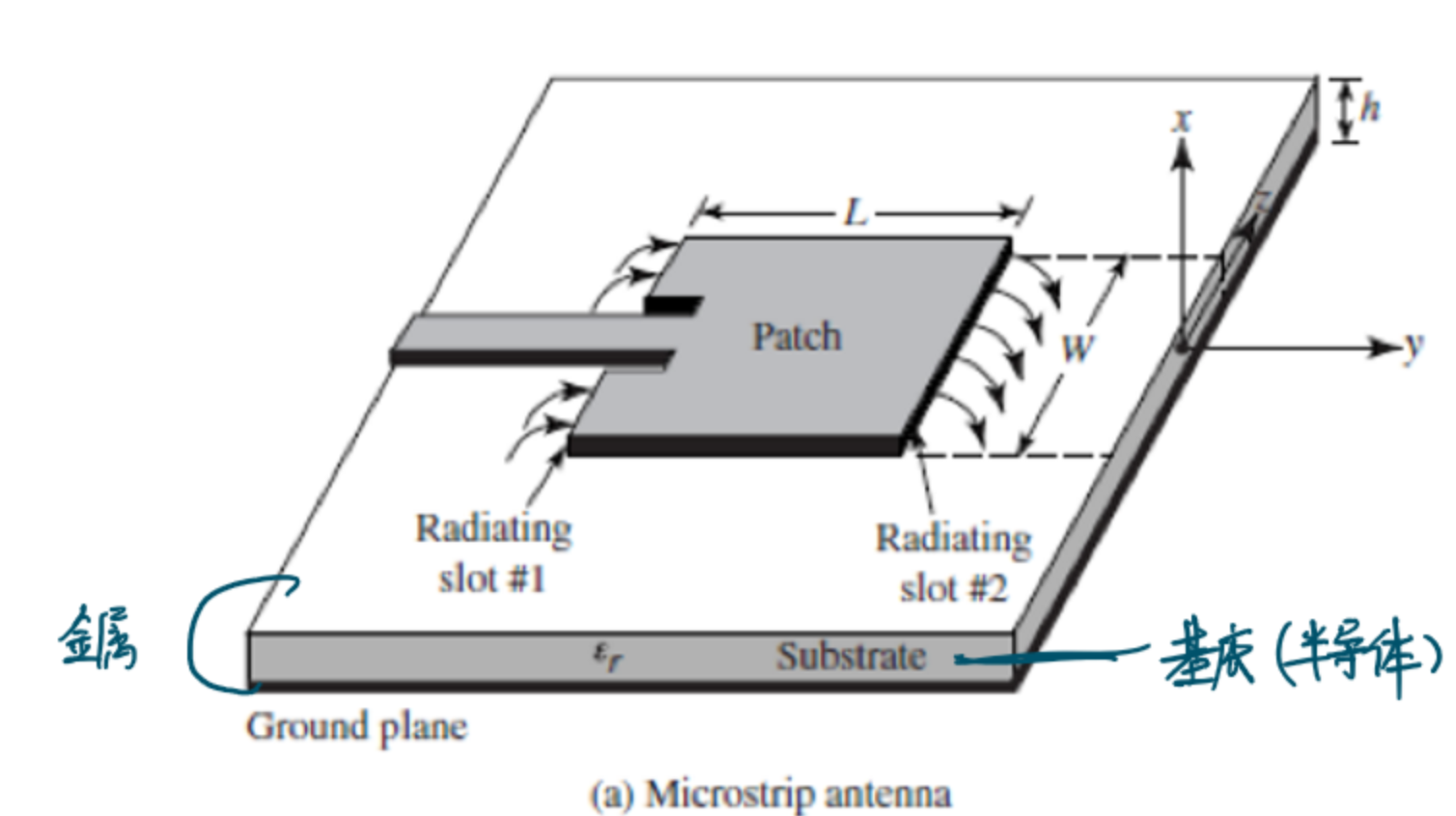
孔径天线

由于直接求解孔径天线是非常复杂的，所以需要用等效方法和惠更斯原理来进行求解。

等效

等效是指用一个封闭的平面将原来的辐射场包围起来，然后在封闭面上放置满足边界条件的适当的电流和磁流密度（电流元和磁流元）。这时边界上的电流和磁流可以唯一确定边界内的场，得到一个等效。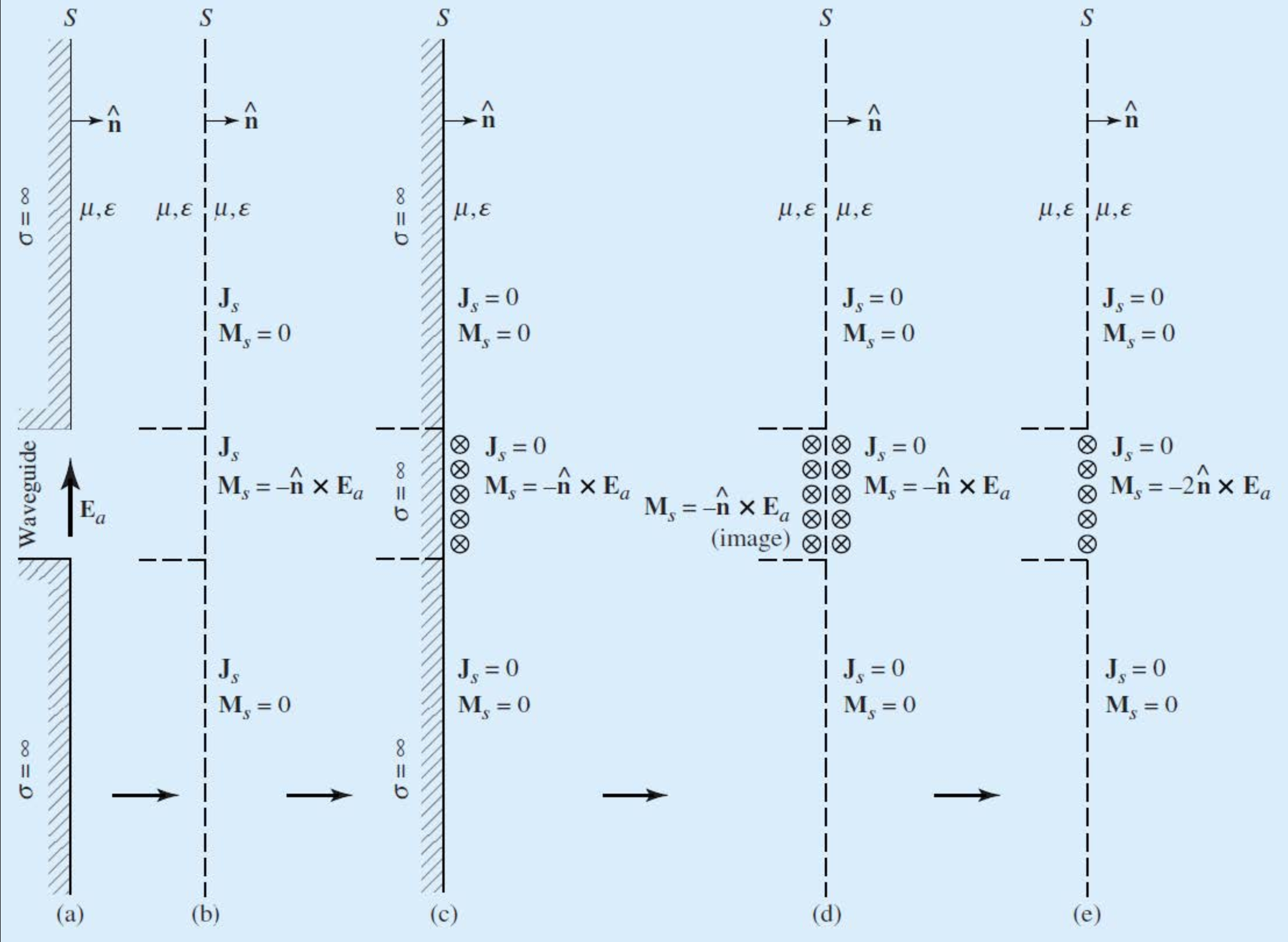

具体而言，如上图所示，假设孔径天线的波导处电场方向\(E_a\)向\(z\)轴方向，根据惠更斯原理假设电流元向\(-x\)轴方向，那么\(J_s=0\)。考虑镜像原理，\(M_s=-2\hat{n}×E_a\)。
因此口径天线的电流密度和磁流密度可以等效为：
\[\begin{cases} J_s=0 \\ M_s=-2\hat{n}×E_a \\ \end{cases}\] \(\hat{n}\): 如图的\(y\)方向上的单位向量

惠更斯原理

波前上每一点都可以看成是一个次级波的新波源。所以在等效过后，就可以通过惠更斯原理求出原辐射源在封闭面外的辐射。

喇叭天线

相移

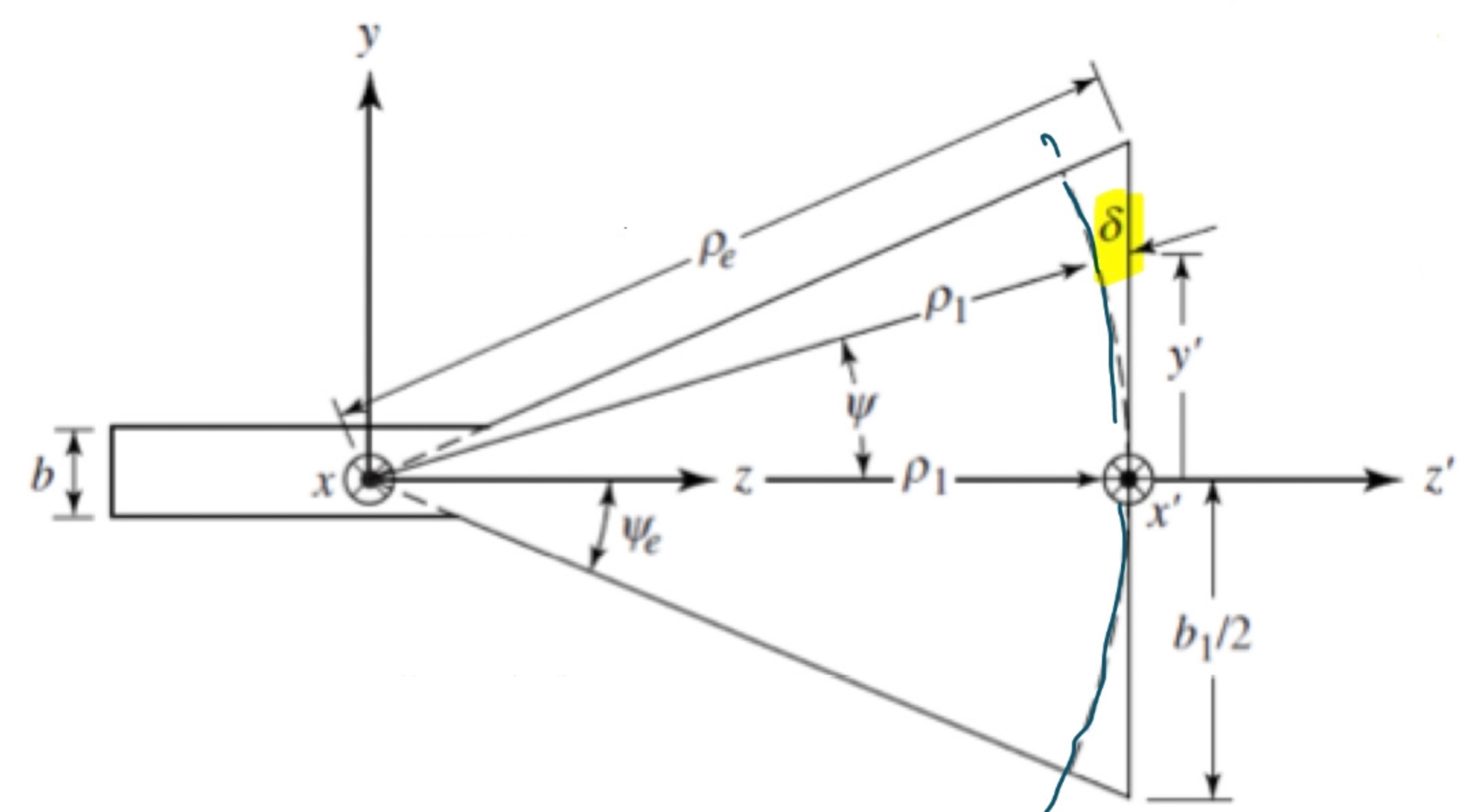
如图为喇叭天线的侧视图，到达\(x'\)的平面波之间的相位差是由距离的不同\(δ\)产生的，\(δ\)与高度\(y'\)有关，记为\(δ(y')\)，称为波程差（Spherical phase term）。
根据如图的几何关系，有：
\[[ρ_1+δ(y')]^2=ρ_1^2+y'^2\] 化简得到\(δ(y')=\frac{1}{2}(\frac{y'}{ρ_1})^2\)。
则波的相位差为：
\(ΔΦ=kδ(y')\) 其中\(k\)为相位常数，在数值上等于波数。 当\(y'=\frac{1}{2}b_1\)时\(δ(y')\)取最大值。

反射天线

抛物面天线

由于抛物面有从焦点到抛物面上任意一点的长度与该点到准线的长度之和始终为定值的特性，因此以焦点为馈电点，到准线的所有电磁波都是平面波。
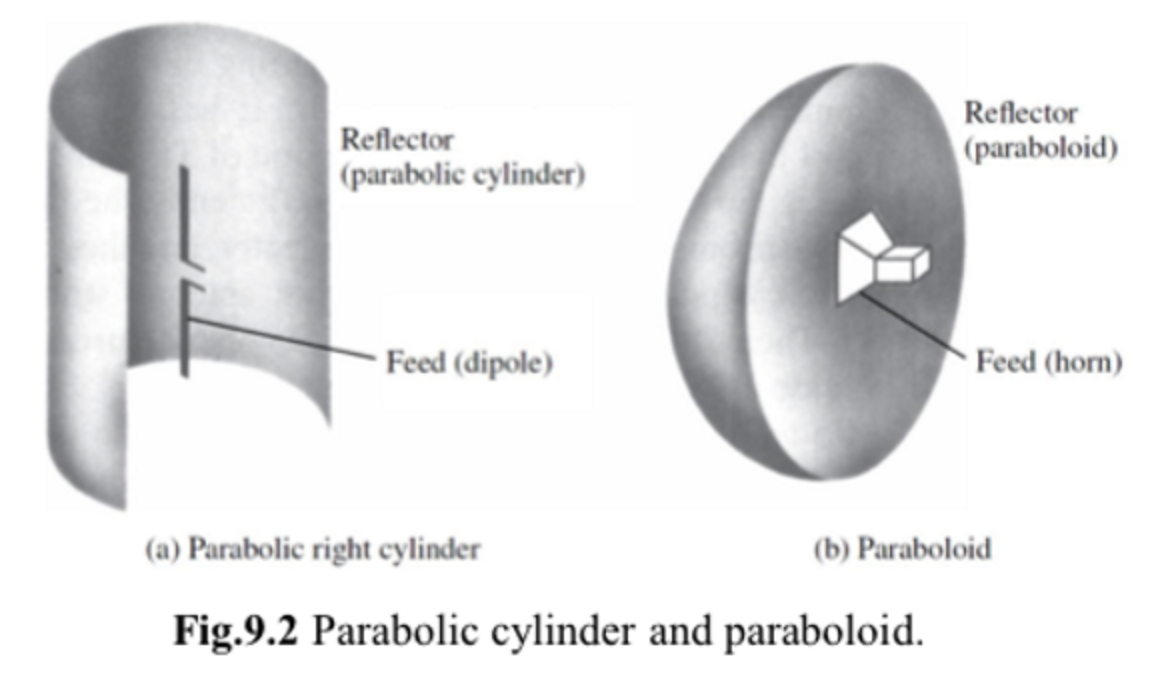
前馈的抛物面天线有两种：抛物柱面（Parabolic cylinder）天线和抛物面天线（Paraboloid）。

名称	振幅函数	馈电源	极化方式
抛物柱面天线	与\(\frac{1}{ρ}\) 呈正比	线形（通常是偶极子天线）	只有线极化
抛物面天线	与\(\frac{1}{r^2}\)呈正比	点	任何极化

与抛物面天线相比，抛物柱面天线的机械结构简单，能提供较大的口径阻挡，没有抛物面天线的吸引特性。

透镜天线

透镜天线的使用频率在1000MHz以上，在3000MHz以上工作效果会更好。
- 优点
- 馈电点和支撑不妨碍传播 - 更大的设计公差（Design tolerance）
- 可以处理比抛物面天线更多的波

• 缺点
  • 笨重
  • 设计复杂
    
  • 比同尺寸的抛物面天线贵
• 应用
  • 宽带天线
    
  • 微波传输

传输基本原理

传输过程的基本参数

真空中的特征阻抗：\(η_0=\sqrt{\frac{μ_0}{ϵ_0}}=120π\)
波数：\(k=\frac{2π}{λ}=ω\sqrt{μ_0ϵ_0}\)
通信链路公式：
\[P_L=(\frac{λ}{4πr})^2P_{in}G_rG_t\]

自由空间传播损耗

\[L_{fb}=10lg\frac{P_t}{P_r}=-20lg\frac{4πd}{λ}\] \[L_{fb}|_{dB}=32.4+20lgf[MHz]+20lgd[km]\] \(d\)：传输距离，\(f\)：电磁波频率

菲涅尔区

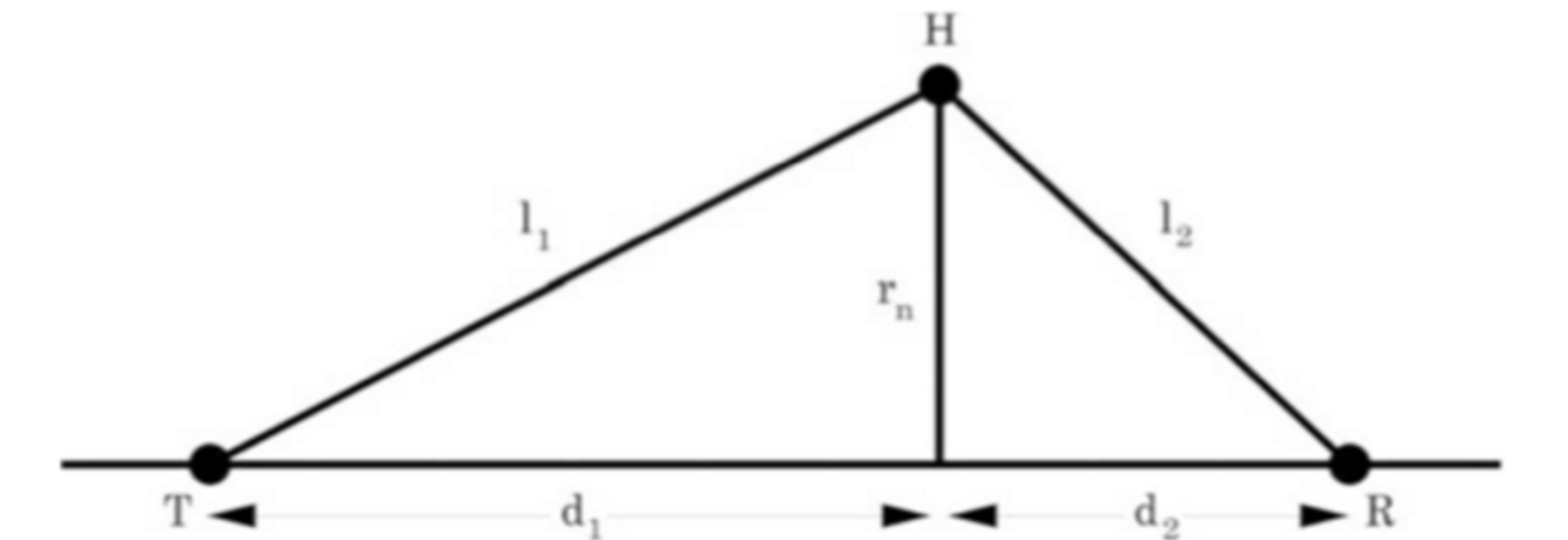
如图，第n菲涅尔区满足条件：
\[l-d=n\frac{λ}{2}\] 当\(d_1,d_2>>λ\)时，原式可以化简为： \[F_n=\sqrt{\frac{nd_1d_2λ}{d_1+d_2}}\]

菲涅尔区允许最大的侵占体积为整个菲涅尔区的40%，侵占体积最好不要超过整个菲涅尔区的20%。

移动通信

移动通信面临的问题是动态且多变的，具体表现为：
- 环境和信号都随着时间不断变化
- 这样的变化是毫无规律的

衰落

移动通信中的衰落主要有两种：
- 长期衰落：在传播中的微小变化通过时间积累后被放大。
- 短期衰落：传播过程中多次反射/多径效应造成的衰落。
短期衰落主要来源于: 障碍物的直接遮挡（阴影效应，Shadow）、接收者的移动、地形（Terrain）、链路的不平衡传输（下行数据速率大于上行）等等。

因此即使是在同一个点，不同时间接收到的信号的能量和场强等也会变化，其变化规律符合正态分布。接收信号的场强可以用\(E_q(dBμV/m)\)表示：

\[E_q=E_m+Q_iσ_L\]
\(E_m\):该点场强的中值，\(Q_i\):指定信号需要覆盖\(q\%\)的衰落储备(Fade Margin)所对应的指数分布系数，可通过查表找到\(q_i\)对应\(Q_i\)，\(σ_L(dB)\):标准差。
其中定义：
\[FM=Q_iσ_L\] 称为衰落储备(Fade Margin)。
接收端移动天线所接收的能量\(P_{rM}\)和敏感度\(P_{rS}\)，衰落储备之间的关系：
\[P_{rM}=P_{rS}+FM\]

多径效应和多普勒效应

由于障碍物的存在，实际上接收的电磁波来源有两类：
- 直接接收到的电磁波
- 通过障碍物和地面的反射接收到的电磁波

由同一传输信号沿两个或多个路径传播，以微小的时间差到达接收机的信号相互干涉所引起的衰落称之为多径衰落。多径效应对信号的幅值、频率、相位都有很大的影响。
多径效应的模型分为三类：静态（接收和发射都静止），半动态（接收运动），动态（接收和发射都运动）。

在动态模型中，需要考虑多普勒效应对观察频率\(f_d\)的影响：
\[f_d=f_mcosθ\] \(f_m=\frac{V}{λ}\)：最大多普勒频率，\(θ\):波和运动方向的夹角。

多普勒效应会对信号产生频移，不同的多径信号上存在时变的多普勒频移，如果信号由于多普勒效应产生的频移大于信道的时分复用周期，用户将接收不到信号。

通信链路

简单来说，接收的能量等于发射的能量加上传输增益、减去传输损失。
通信链路分为上行链路和下行链路，由于上行和下行设备的不同因此需要分开计算。
传输损失小的一方覆盖更大，最终链路的覆盖由损失更大的一方决定。

上行链路

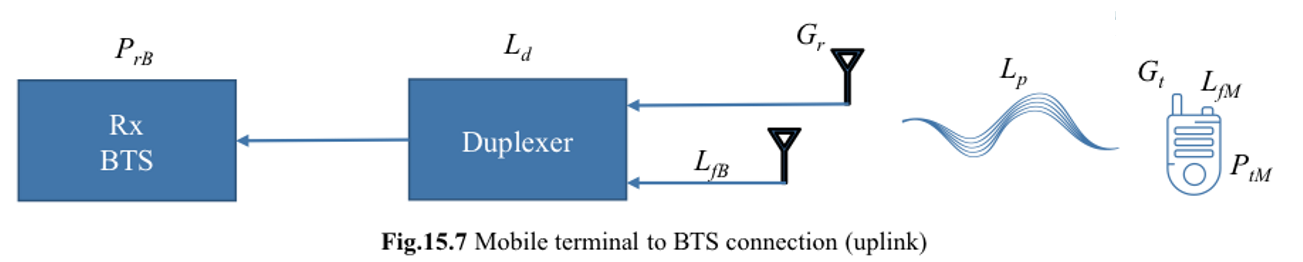
如图所示：
\[P_{rB}=P_{tM}-L_d-L_p-L_{fM}-L_{fB}+G_t+G_r\]
\[P_{rB}+FM=P_{tM}-L_d-L_p-L_{fM}-L_{fB}+G_t+G_r\]

下行链路

下行链路需要用多路耦合器（Multi coupler）将多个用户的信息进行整合，此处会有传输损失\(L_c\)。
如图所示：
\[P_{rM}=P_{tB}-L_c-L_d-L_{fB}-L_{fM}+G_t+G_r\]
\[P_{rS}+FM=P_{tB}-L_c-L_d-L_{fB}-L_{fM}+G_t+G_r\]

区域覆盖预测模型

区域覆盖预测模型有三种：经验模型（Empirical model）、确定性模型（Deterministic model）、和射线追踪模型/半确定性模型（Physical-statistical/Ray-tracing model）。

名称	特点
经验模型	1.基于实验测量 2.结果通常是基于有限的频率和一些特定的介质 3.缺乏对无线电波传播机制的物理观点(Physical view)
确定性模型/射线追踪模型	1.应用十分有限，主要应用于特殊几何结构的情况 2.对不同情况需要不同的传输路径特性(如ɛ和σ) 3.由于考虑了直射、折射和衍射，因此模型十分复杂 4.考虑了不同地形的电参数
半确定性模型	两者的折中方案

电磁波在介质中的实际传输

在实际情况下，根据电磁波的传输介质，电磁波可以分为：空间波、天波、地表面波三类，其频率、传播环境和应用如下表所示。

类型	频率	传播环境	应用
空间波	30MHz	视距无线传输(Line of sight)	微波通信、广播、导航
天波	3-30MHz	电离层(Ionosphere)	长距离通信、广播
地表面波	2MHz	地表面	短距离通信、报时信号

地表面波

特征

• 水平极化的地表面波衰减很大，并没有实用价值。因此基于地表面波的大部分应用都是基于地表面波的垂直极化。
• 向前传输
  地表面波可以分解为\(E_z\)和\(E_ρ\)两个方向上的波，由于\(E_z>E_ρ\)，因此两者的矢量和始终是向前的。
  地面以上部分的地表面波是椭圆极化：地表面波由径向分量和垂直分量组成。径向分量相对较小，相位差近似为零，形成椭圆偏振。

地表面电参数

• 土质
  
• 湿度
  
• 温度
  
• 能量吸收的能力
  
• 地表面类型对传播的影响
• 地表面的导电性越好，传输过程中的衰落就越小。
• 波的频率越高，传输过程中的衰落越大。

天波

大气层结构

• 对流层（Troposphere）
  这一层主要对电波有 吸收、衰减、折射、反射、极化改变、散射等等影响。
  
• 电离层（Ionosphere）
  这一层内部有许多的等离子体（plasma）/电离气体（Ionized gas）以防护宇宙射线。
  电离层能够极大的改变电磁波的电性质。
  电离层自身处于动态且周期性的变化中。
  天波主要在这一层进行传播。天波的内部分为多个小层：

名称	距离	注解
D	50-70km
E	70-100km	等离子体密度达到最大相对值 对电波传输的影响白天比晚上强，夏天比冬天强
F	1000km	等离子体密度再次达到相对最大值

• 在白天F层会分成\(F_1\)和\(F_2\)两个子层，在晚上这两层又会重新合并。
  在白天，D层的下部对中频电波的损失非常的大，因此在中频和高频通信中往往选用频率比较高的电磁波（Lower frequency in MF band）。由于F层在白天分层的特性，中频通信中使用的较低频率的电磁波只能在晚上传输，白天通常传输中频/高频通信中的较高频率的电磁波（Higher frequency in MF band）。

电离层中的传播

定义电离层中的等离子体谐振角频率、频率\(ω_p\)、\(f_p\)，那么电离层的介电常数可以由如下公式界定：
\[ɛ_r=1-\frac{f_p}{f}\] 电离层中的传输常数\(k_c\):\(k_c=k_0√{1-(\frac{f_p}{f})^2}\)

• 垂直发射
  电离层中的平面波电场可以简化为：\(E=E_0e^{-jk_cz}\) 垂直发射电磁波，当电磁波频率小于\(f_c=9√N,N\)：等离子体密度时，电磁波将无法穿过电离层并且反射回地球。
  
• 斜向发射
  
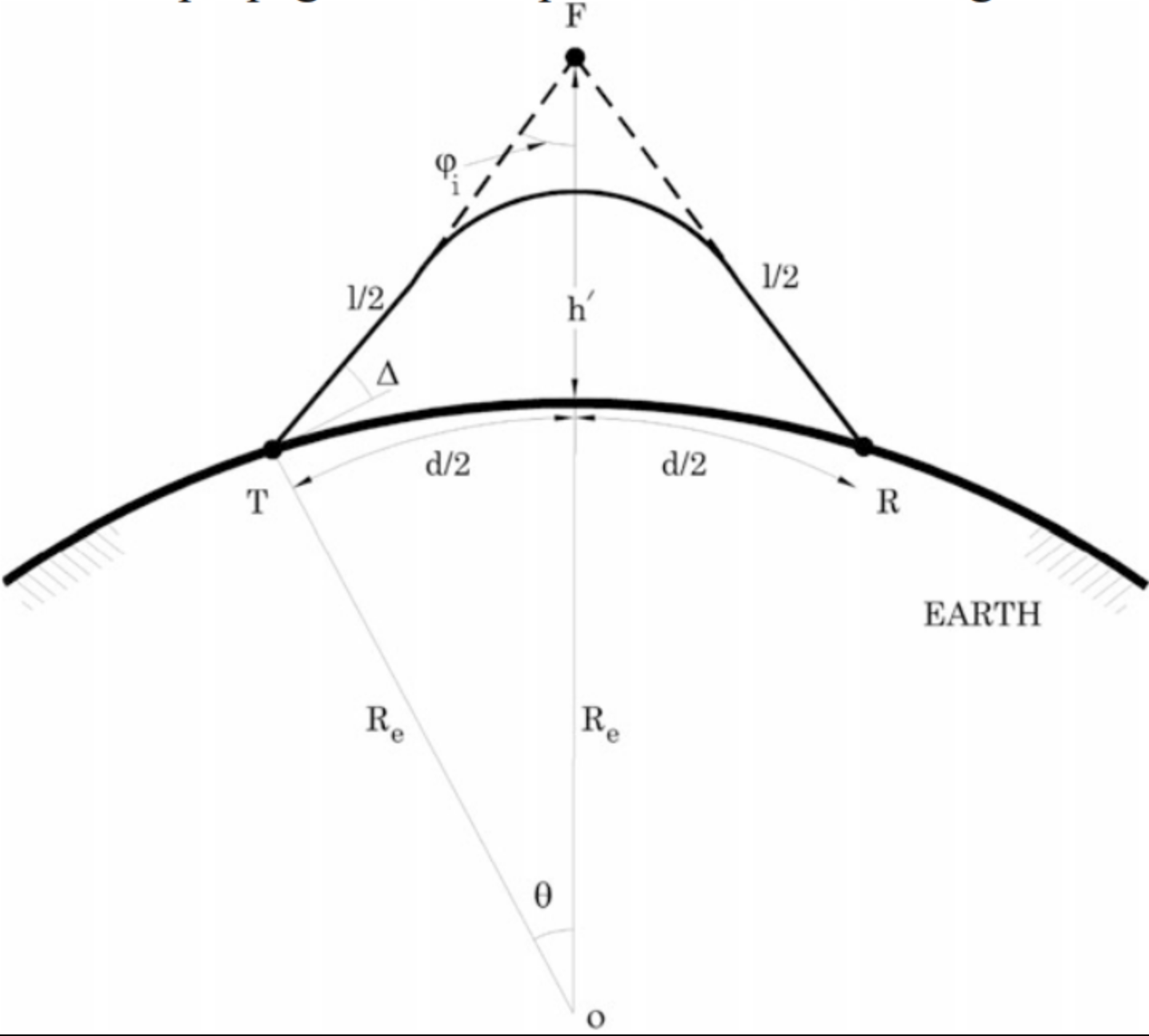
  斜向发射电磁波时，这一最大频率取决于电磁波的入射角\(Φ\)(上图中的\(ϕ_i\))和\(f_c\)，定义斜向发射时的最大可用频率MUF:
  \[MUF=f_c×secΦ\] 在发射矢量与地球相切（发射仰角\(Δ=0\)）时，认为\(Φ=74°\) \[MUF=f_c×secΦ=3.6f_c\] 由于各种因素的影响，定义最佳电磁波频率OUF： \[OUF=MUF×(50\%-80\%)\]

  如果题目中没有告诉百分比，默认取80%

实际上，电磁波的斜向传输是通过在地面和电离层之间来回多次反射进行的，每一次反射能跨越的距离主要受三个因素影响：
- 发射频率
- 电磁波的仰角（Elevation angle）
- 电离层中多个小层的变化