04. 高斯噪声

高斯噪声

白噪声

白噪声指噪声信号的功率谱密度函数在频域内符合均匀分布。事实上，完全意义上的白噪声是不可能存在的，因此如果噪声的功率谱密度在系统的工作频段内符合均匀分布，也认为是白噪声。
### 白噪声的统计特性 白噪声的谱密度函数（双边）可以表示为：
\[P_ξ(ω)=\frac{n_0}{2}(-∞<ω<∞)\] 其期望为：
\[E_ξ(ω)=∞\] 其自相关函数为：
\[R_ξ(τ)=\frac{1}{2π}∫_{-∞}^∞\frac{n_0}{2}e^{jωτ}dω=\frac{n_0}{2}δ(τ)\] 频谱中为负的部分没有任何的现实意义，因此定义白噪声的单边谱密度函数为：
\[P_ξ(ω)=n_0(-∞<ω<∞)\]

高斯白噪声

高斯白噪声指信号的功率谱密度函数在频域内符合均匀分布、概率密度函数符合高斯分布的噪声。高斯白噪声是一种可加性噪声。

高斯白噪声的统计特性

均值：\(E_ξ(ω)=0\)
方差：\(D_ξ(ω)=0\)
自相关函数：\(R_n(τ)=\frac{n_0}{2}δ(τ)\)

窄带高斯白噪声

当高斯白噪声通过线性滤波器从而使得原有的谱密度函数说遵循的均匀分布被限制在了某一个频段\((-ω,ω)\)，称此时的高斯白噪声为窄带高斯白噪声。

表达方式和统计性质

包络相位形式

窄带高斯白噪声的谱密度函数可以表示为：
\[n_i(t)=a(t)cos[ω_ct+ϕ(t)]\] 其中\(a(t)\)是随机包络函数，\(ϕ(t)\)是随机相位函数。

随机包络和随机相位的统计特性：
随机包络\(a(t)\)：
\[f(a)=\frac{a}{σ^2}exp[-\frac{a^2}{2σ_n^2}],a≥0\] 其服从瑞利分布。
随机相位\(ϕ(t)\)：
\[f(ϕ)=\frac{1}{2π},0≤ϕ≤2π\] 其服从均匀分布，且与随机包络相互独立。

同相正交形式

定义窄带高斯白噪声的
同相分量：\(n_c(t)=a(t)cos[ϕ(t)]\)
正交分量：\(n_s(t)=a(t)sin[ϕ(t)]\)
则窄带高斯白噪声可以分解为：
\[n_i(t)=n_ccosω_ct-n_s(t)sinω_ct\]

同相分量和正交分量的统计特性：
一个均值为0的窄带平稳高斯过程，其同相分量和正交分量也是平稳高斯过程，且均值为0，方差和原信号相同。

高斯白噪声通过低通滤波器

低通滤波器的频谱是一个以\(ω=0\)为纵对称轴轴的门函数，其截止频率为\(W\)：

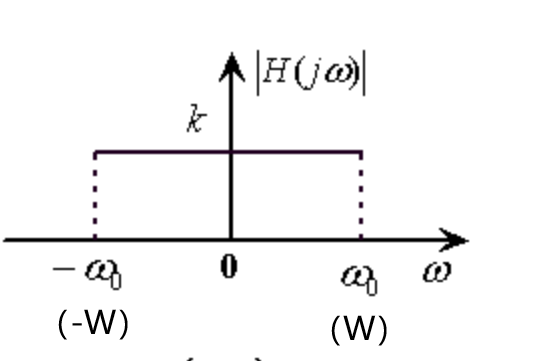
按照第3讲中平稳随机过程通过线性系统的输出特性，可以得到当输入高斯白噪声到低通滤波器时，输出的窄带高斯白噪声的谱密度函数：
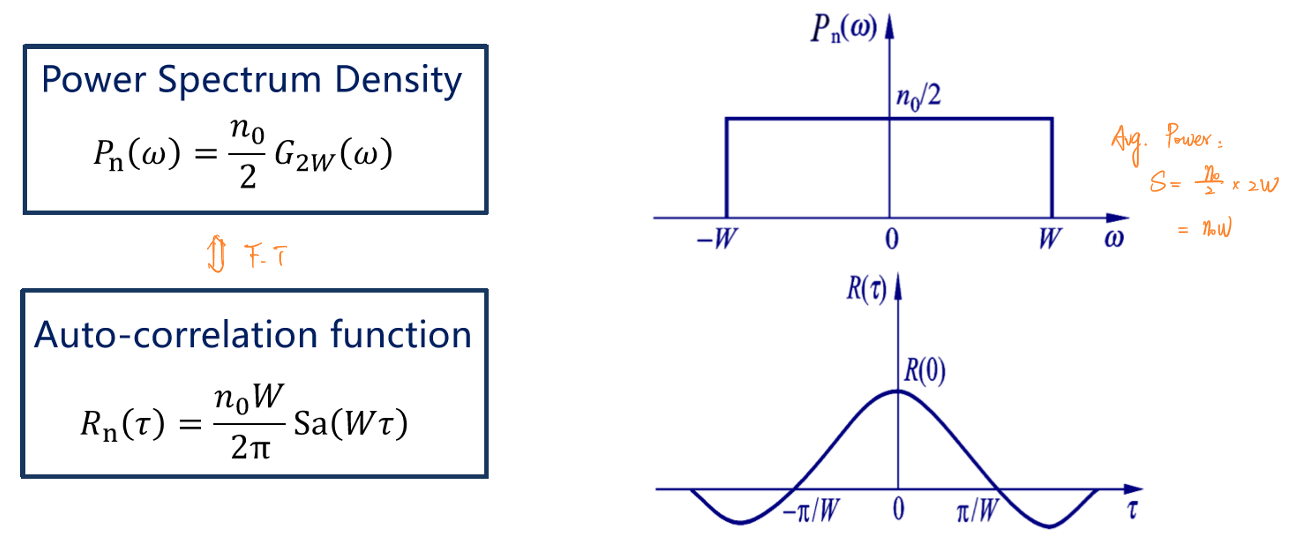
\[P_ξ(ω)=\frac{n_0}{2},-W≤ω≤W=\frac{n_0}{2}G_{2W}(ω)\] 其中\(W\)表示的是线性低通滤波器的截止频率。
此时的平均功率可以由谱密度函数的面积表示：
\[\overline{P_{ξ}}=\frac{n_0}{2}×2W=n_0W\] 其自相关函数可以通过傅里叶变换来获得：
\[R_n(τ)=\frac{n_0W}{2π}Sa(Wτ)\]

高斯白噪声通过带通滤波器

带通滤波器的频谱是两个以\(ω=ω_0\)为纵对称轴轴的、且相互以\(ω=0\)对称的门函数，其截止频段为\(W\)：

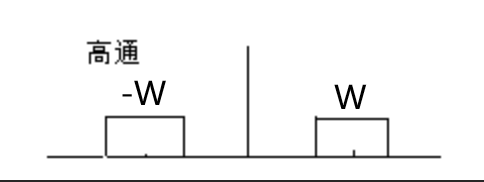
当高斯白噪声通过带通滤波器，其输出的窄带高斯白噪声的谱密度函数为：
\[P_n(ω)=\frac{n_0}{2}[G_W(ω+ω_0)+G_W(ω-ω_0)]\] 由傅里叶变换得到其自相关函数为：
\[R_n(τ)=\frac{n_0W}{2π}Sa(\frac{Wτ}{2})cos(ω_0τ)\] 其平均功率为：
\[Avg.Power=\frac{n_0}{2}×2×W=n_0W\]