讲义：什么是遗传算法（GA）？

讲义：什么是遗传算法？

参考资料： 1. Flappy Learning- https://xviniette.github.io/FlappyLearning 2. 北京大兴国际机场旅客航站楼和综合换乘中心, 北京市建筑设计研究院有限公司 3. Technological overview of the next generation Shinkansen high-speed train Series N700, Central Japan Railway Company, Tokyo, Japan 4. Towards Safe Evolutionary Optimization, Chao Qian, Nanjing University 5. 'Genshin Impact': Building a Scalable AI System, Shou Xu, miHoYo Inc., 2021 6. 遗传算法在游戏开发中的应用，杨科选等，中科院软件研究所，2009⋆ 7. 遗传算法原理及应用，周明等，国防工业出版社，1999⋆ 8. A genetic algorithm tutorial, Darrell Whitley, 1994⋆ 9. 自然与人工系统中的适应:理论分析及其在生物控制和人工智能中的应用,John.H.Holland ,高等教育出版社，2008⋆ 10. Adaptation in Nature and Artificial Systems,John.H.Holland, A Bradford Book, 2008 （9的英文版）⋆

这是Brunel University London EE1619：Engineering Science, Systems and Society（工程科学、系统与社会）面向大一学生的一节Seminar的中文讲义。
本文中避免了对于Holland博士提出的经典遗传算法收敛性的讨论，省略了交叉、突变对于算法收敛性的改进作用；并在有效性方面只介绍了模式定理，还请读者注意。

引入

学习目标

1. 了解一些遗传算法的应用案例
2. 了解经典遗传算法的运行流程
3. 使用数学方法证明经典遗传算法的有效性
4. 对遗传算法进行评价：知晓其优点和缺点

遗传算法的定义

遗传算法是一类将特定问题潜在的解决方案编码，然后应用进化理论对解决方案进行优胜劣汰式的反复筛选的算法。

遗传算法的应用

Github 开源项目FlappyLearning

项目地址：https://xviniette.github.io/FlappyLearning/
项目通过每一代生成50个flappy bird，每一只鸟由随机的操作进行控制，通过游戏对其进行淘汰，而能够活得久，获得高分的游戏策略会有高概率继承给下一代。
大约在第25-50代时的鸟能够稳定地存活下去。
在游戏设计中，有些怪物可以应用遗传算法随机切换攻击模式，并通过进化和玩家的对抗不断地筛选出不容易被玩家打败的攻击模式，从而提升游戏可持续的难度。

大兴机场穹顶力学结构设计

大兴机场的穹顶设计使用了遗传算法来符合力学要求。具体而言，大兴机场的穹顶在在设计时，穹顶的主划分线被赋予了88个控制点，遗传算法可以对这88个控制点的位置进行选择，使建造出的穹顶不会倒塌。

新干线N700系车头外形

高速铁路列车在通过隧道时由于列车和隧道对空气的挤压发出巨大的响声，新干线N700系列车在设计时通过遗传算法对列车的外形进行选择，最终设计出抗噪性较好的列车外形。

遗传算法的概念

举例：遗传算法面对的问题

开始之前，我们需要明确几个概念。
思考如下的场景：我们需要从一口井中取水，井中水的水位是由一个水阀进行控制，这个水阀有8个档位，每一个档位对应了不同的水位高度，要想更方便地取水自然水位的高度越高越好，现在我们想要找到那个最适合我们取水的档位，就可以用遗传算法解决这个问题。
在遗传算法中，这个水阀的8个档位实际上就是系统的八种状态，这八种状态对应了系统不同的输出，像这样的，系统的某些或全部状态的集合称为一个种群（Population）。 称这个状态集合中的一个特定状态为个体（Individual）或者染色体（Chromosome）。
> 此处要注意与生物学上个体和染色体的数量关系进行区分，遗传算法领域认为一个个体只含有一条染色体。

经典遗传算法的流程

经典遗传算法通过对当前种群的评估（Evaluation），选择（Selection），重组（Recombination）和突变（Mutation） 后，能够在现有种群的基础上产生下一代种群。经过数次进化之后，遗传算法能够选择出对目标问题解决的最佳方案组合。

状态编码

当然，计算机是无法直接读懂这些状态的意义，对数学运算而言，函数的自变量也必须是一个数，因此需要对系统的所有状态进行编码（Coding）。编码的过程就是将状态用数进行编号的过程。 遗传算法中采用的编码机制是二进制编码，如上面例子当中水阀的8个档位，就可以用3个比特位（称为位串（Strings））：从000 编码到111，对这个水阀的8个档位状态进行表达。
种群中的每一个个体都可以用位串的形式进行表达。
编码之后的个体就能够用函数去评估它是好的还是坏的了。

原始种群

由于实际问题中遗传算法要面临的状态编码数量非常庞大，不可能一下子对所有的状态都进行评估，因此遗传算法需要从所有个体中随机地抓取一些个体生成原始种群（Initial population）。遗传算法最开始的操作都是对原始种群进行的。

评估和适应度

原始种群被生成后，每一个个体会通过评估函数和适应度函数（Fitness funtion）生成其对种群的适应度（Fitness）。

对适应度函数的直观理解：
我们想要从一个班的学生中选择出优等生，最简单的方法就是考试，每个学生通过考试会得到一个分数，以衡量他们的学习水平。在这里，考试就是适应度函数，而每个学生的分数就是适应度。

种群中个体\(i\)的适应度定义为：
\[\frac{f_i}{\overline{f}}\]
其中，\(f_i\)表示评估函数对第\(i\)个个体的评估结果，\(\overline{f}\)表示种群的平均评估。
个体的适应度越高，表明这个状态对应的系统结果越能够符合我们的要求。

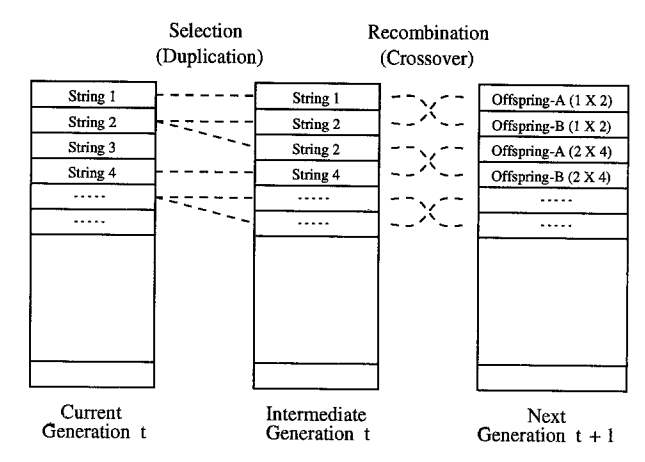
复制·选择（余数随机采样）

选择后的每个个体的适应度格式为x.xx，即有小数部分和整数部分。适应度的整数部分表示该个体会被复制多少次。 复制中的选择机制：
这样就能直接地让优秀的个体获得更多被复制的机会，而适应度整数部分为0的个体因为不会被复制而被淘汰。
但是，那些适应度比较低的个体中仍然可能有对系统有益的部分，为了尽可能地保留这些部分，遗传算法在选择阶段还规定：
对所有的个体，适应度的小数部分表示额外被复制的概率。
如此，每一个个体中对系统有益的部分都能够被尽可能地复制。
比如，适应度2.3的个体能够获得2次复制，并且有0.3的概率能获得第三次复制的机会。
这样的机制能够用数学表示为：
\[M(H,t+1)=M(H,t)\frac{f(H,t)}{\overline{f}}\]
其中M表示的是种群中的一个亚种(Sub-populations)。

总结：
选择的过程即为有概率地对种群中的个体进行复制，可以发现，适应度越高的个体被复制的概率就越大。

原始种群经过复制后形成中间种（Intermediate Generation）。

重组（单点交叉）

遗传算法中重组的本质是杂交（Crossover），其过程主要有两步： 1. 随机地使得个体间两两配对。
2. 随机地选取一对个体，两者在某个随机且相同的比特位处断开，前后的两段基因型进行交叉互换。

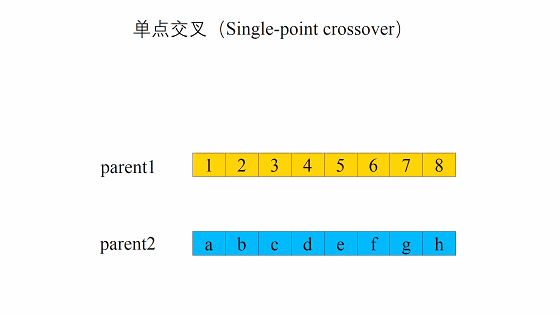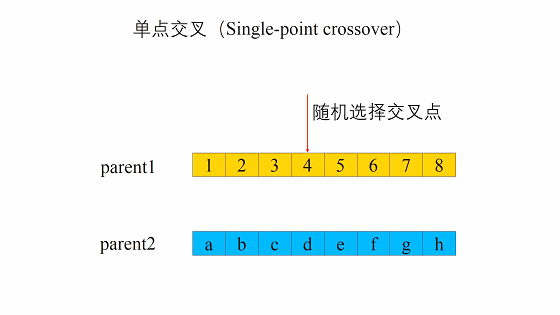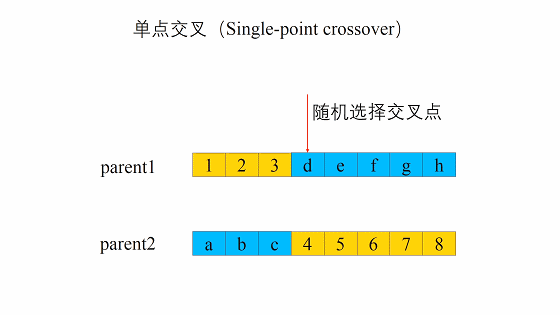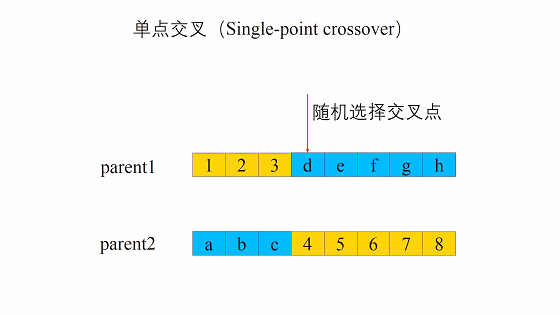
新生成的两个个体称为后代（Offspring），后代能够插入到下一代的概率计作\(p_c\)。

突变（反转突变）

重组之后利用突变算子对后代作突变处理，对于种群中的所有比特位，其有\(p_m\)的概率发生比特反转。同遗传学一样，突变概率一个非常小的概率，通常小于1%。
中间种经过重组和突变，最终能称为新的种群。

▲ 经典遗传算法的选择和重组过程

遗传算法的有效性证明

上述的过程中很难直观地让我们感受到重组和突变对算法带来的实际效果，也很难感受到遗传算法的有效性，下面从数学的角度说明这两点。

采样空间

在几何学上，称n维空间的某一个小于n维的子空间为超平面（hyperplane）， 比如二维空间的超平面是一条线，三位空间的超平面是一个面。
在位串长度固定位\(L\)的前提下，种群中所有可能的编码方式所构成的空间称为搜索空间（Search space）。 如果每一种特定的编码方式在L维搜索空间中对应了一个角（Corner），那么共超平面的几个角对应的编码中必定在相同的某几个比特位上的值是相同的，此时引入通配符（Don‘t care，以*记）的概念，那么搜索空间的一个超平面就可以表示为含有Don't care（*）的位串（比如：0****，11*****），这样的位串称为模式（Schema），每一个模式对应了一个超平面。

模式定理

适应度选择

由之前提出的经过选择后超平面\(H\)留存的样本（个体）数目\(M(H,t+1)\)：
\[M(H,t+1)=M(H,t)\frac{f(H,t)}{\overline{f}}\]

重组的作用·定义距

考虑重组对选择后超平面\(H\)中种群样本数目的影响： 1. 重组是有概率发生的，概率为\(p_c\)。
2. 对于发生重组的种群，交叉既有可能产生出现有空间内某个模式的副本（比如100和010交叉就可能产生000，使得000的副本增加一个）即为\(gains\)，单位为个数，同时也有可能使得原有的样本消失，这个消失的概率记为\(losses\)。

那么现在后代中落在超平面\(H\)的样本数目：
\[M(H,t+1)=(1-p_c)M(H,t) \frac{f(H,t)}{\overline{f}} +p_c [M(H,t)\frac{f(H,t)}{\overline{f}}(1-losses)+gains]\]

模式定理认为gain发生的概率要远远小于losses。为了简化计算，忽略gain，并且假设发生在Schema上有义部分的交叉必然导致染色体破坏，记破坏概率为\(disruption\)，那么有：
\[M(H,t+1) \geq (1-p_c)M(H,t) \frac{f(H,t)}{\overline{f}} +p_c [M(H,t)\frac{f(H,t)}{\overline{f}}(1-disruption)]\] 定义超平面\(H\)的采样率表示超平面\(H\)的样本数目与种群中样本数目的比，以\(P(H,t)\)记。

定义距\(Δ(H)\)表示超平面\(H\)对应模式中第一个确定字符的位置和最后一个确定字符的位置之间的距离。如：\(Δ( 011 ∗ 1 ∗ ∗ )=4\)。
按照我们对重组的理解：对原信息的破坏只可能发生在定义距的区间段内。

此外，如果发生重组的位串都在平面\(H\)内，那么重组也不可能对原本信息造成破坏，因此要想让重组破坏原有的信息，亲本中的另一条位串必定来自于其他平面，另一个位串来自其他平面的概率为\(1-P(H,t)\)。
由这上述两点可以将破坏概率定义为：
\[\frac{\Delta(H)}{L-1}(1-P(H,t))\] 由破坏的定义可以得出如下结论：
定义距\(Δ(H)\)越小，模式受到破坏的概率就越小。从直观上来说，定义距越小，交叉发生在定义距内（即一定能破坏信息）的概率也越小。
那么下一代超平面\(H\)的采样率可以表示为： \[P(H,t+1) \geq P(H,t) \frac{f(H,t)}{\overline{f}} [1-p_c \frac{\Delta(H)}{L-1}(1-P(H,t))]\]
如果考虑亲代是基于适应度选择出来的：
\[P(H,t+1) \geq P(H,t) \frac{f(H,t)}{\overline{f}} [1-p_c \frac{\Delta(H)}{L-1}(1-P(H,t)\frac{f(H,t)}{\overline{f}})]\]

突变的作用·模式阶

最后，考虑突变的影响：记突变发生的概率为\(p_m\)，超平面\(H\)的阶数为\(o(H)\)，阶数表示模式中确定字符的个数，当突变发生在这些字符上时，才会对原来的位串产生破坏。
那么表示超平面\(H\)的Schema不会受到突变影响的概率为：
\[(1-p_m)^{o(H)}\] 可以得出结论：
模式的阶数\(o(H)\)越小,模式不会受到突变影响的概率越大。从直观上来看，模式的阶数代表着有效字符的个数，有效字符越少，在交叉过程中越容易被保留下来。
最终，超平面\(H\)在下一代中被采样到的概率可以表示为：
\[P(H,t+1) \geq P(H,t) \frac{f(H,t)}{\overline{f}} [1-p_c \frac{\Delta(H)}{L-1}(1-P(H,t)\frac{f(H,t)}{\overline{f}})] (1-p_m)^{o(H)} \]

指数增长

可以通过数学推算出，在适应度\(\frac{f(H,t)}{\overline{f}}>1\)时： \[P(H,t) \frac{f(H,t)}{\overline{f}} [1-p_c \frac{\Delta(H)}{L-1}(1-P(H,t)\frac{f(H,t)}{\overline{f}})]=P(H,t) \frac{f(H,t)}{\overline{f}}(1-p_c \frac{\Delta(H)}{L-1})+[P(H,t) \frac{f(H,t)}{\overline{f}} ]^2\] 用\(t=0\)代来推算\(t\)代时候的采样率：
\[P(H,t) ≥ \{P(H,0) \frac{f(H,0)}{\overline{f}}(1-p_c \frac{\Delta(H)}{L-1})+[P(H,0) \frac{f(H,0)}{\overline{f}} ]^2\}^t(1-p_m)^{o(H)}\] 可以发现：在适应度\(\frac{f(H,t)}{\overline{f}}>1\)时，采样率呈现指数型上升。
可以总结为：
在选择、重组、突变算子的作用下，当某个超平面的适应度大于1时，模式的阶数\(o(H)\)越小，定义距\(Δ(H)\)越小的个体越能够被保留下来，且数目成指数型上升。
定义距和模式阶都是染色体本身的参数，通过重组和突变这两个参数被引入到进化中，并对选择起到了关键的作用。

对模式定理结论的直观理解

定义距相当于基因的长度，基因越长，在进化过程中被破坏概率就越大，因此定义距越短的个体越容易在进化中得到保留。
例子：兔子的性状
模式阶相当于个体携带性状的个数。单纯的红眼兔显然比裂唇长耳红眼兔更容易传递给后代。因此模式阶越小，个体越容易在进化中得到保留。

模式定理在数学上证明了重组和突变的有效性，并给出了采样率的下界，是遗传算法中重要的理论基础之一。

其他进化算法

Genitor 算法

进化策略中细分为两种类型：\((μ+λ)-ES\)和\((μ,λ)-ES\)。
在\((μ+λ)-ES\)机制中，亲代\(μ\)产生后代\(λ\)后，种群还会对亲代和后代共同进行选择，选择其中表现出色的个体生成下一代。在这种选择机制下，亲代会被保留直到被比亲代表现更出色的个体替代。
在\((μ,λ)-ES\)机制中，后代被产生后就直接替代亲代，选择在后代中执行。这种进化机制在选择阶段与经典遗传算法近似。但是在重组阶段所采用的算子与经典遗传算法不同。
\((μ+λ)-ES\)机制相比于\((μ,λ)-ES\)机制，其被优化的后代数目一定是单调增加的。

传统的进化算法在进行到最后时，由于留存的都是表现的比较好的个体，因此采用适应度淘汰个体（即选择过程）的压力会随着算法运行次数的增加而不断减弱，最后甚至根本不能对个体有任何选择。Gnitor算法可以加强选择的压力，一定程度上避免这种情况的发生。
Genitor算法是一种使用\((μ+λ)-ES\)机制的算法，其与经典遗传算法中的进化模型不同点有三处。
1. 选择在亲代中执行，选择后的亲代产生的后代被立即投放到下一代种群中。
2. 后代不会替代亲代，但是每一代中适应度最差的个体被直接移除以加强选择压力。
3. 适应度函数通过排名算法（Ranking）而非比值来表现。排名也同样能够保持选择压力的有效性。

排名算法

设三个个体的适应度评估为：\(h_1,h_2,h_3\).
首先对所有个体按照适应度从小到大排序，比如：\(h_2,h_1,h_3\);
按照上面的顺序重新赋予fitness，即\(f(h_2)=1,f(h_1)=2,f(h_3)=3\)
计算选择概率:\(p(h_2)=\frac{1}{1+2+3}=\frac{1}{6},p(h_1)=\frac{2}{6},p(h_3)=\frac{3}{6}\)
排名算法能够不受制于适应度的限制，选择压力不会因为总体适应度的上升而减小，保证了选择的有效性。
同时排名算法的运行机制也参考了适应度，保证了选择的可靠性。

锦标赛（Tournaments）算法

1. 确定每次选择的个体数量N。（二元锦标赛选择即选择2个个体）
2. 从种群中随机选择N个个体(每个个体被选择的概率相同) ，根据每个个体的适应度值，选择其中适应度值最好的个体进入下一代种群。
3. 重复步骤(2)多次（重复次数为种群的大小），直到新的种群规模达到原来的种群规模。 锦标赛算法相当于是有噪声的排序算法。
   由于2这一步可以同时选择若干个体数量为N的组，每一组内的选择是独立的，因此通过锦标赛算法可以将遗传算法进行并行化处理，大大地节省了运算时间。

遗传算法的局限性

计算量问题

对于遗传算法来说评估函数的计算速度和计算量是一个问题：首先，对于现有种群的评估计算量就比较大。不仅如此，种群的后代也需要进行评估——这会导致计算量的暴增。

信息表达问题

遗传算法的每个个体用位串来表示，能够存储的信息量、用于描述单个个体的精度有限。