05. 模拟基带信号的线性调制方法

模拟基带信号的线性调制方法

调制

简单来说调制是将原本的信号（称为基带信号）\(m(t)\)与另一个确知信号（称为载波）\(c(t)\)一同进入乘法器，输出信号的过程。
\[S_m(t)=m(t)c(t)\] 需要注意的是，由于载波是确知信号，因此调制过程不会发生任何信息的变化。
使用调制的目的有三个：
1. 由于天线与传输信号的波长之间存在匹配关系，通常天线的尺寸在\(\frac{λ}{10}\)到\(\frac{λ}{4}\)之间，经过调制的信号波长会变小，因此对应的传输天线的尺寸会对应减小以便于传输。
2. 调制使得多频复用称为可能，多个基带信号可以与不同的载波结合，实现同时传输多个基带信号。
3. 扩展信号带宽，提高系统抗干扰能力。

调制方法的分类

• 按基带信号的类型分为：数字调制和模拟调制
• 按照载波信号的类型可分为：连续波调制和脉冲调制
• 当载波为正弦波时，按照正弦波的受调参量可分为：

调制参量	模拟信号调制方法	数字信号调制方法
幅度(A)	AM,DSB,SSB,VSB	ASK
频率(ω/f)	FM	FSK
相位(ϕ)	PM	PSK,DPSK,QPSK,OQPSK

• 按已调信号的频谱结构可分为：线性调制和非线性调制

线性调制及其解调方法概述

线性调制后，不会有新的频率成分产生。因此线性调制只能在受调参量为幅度时使用。
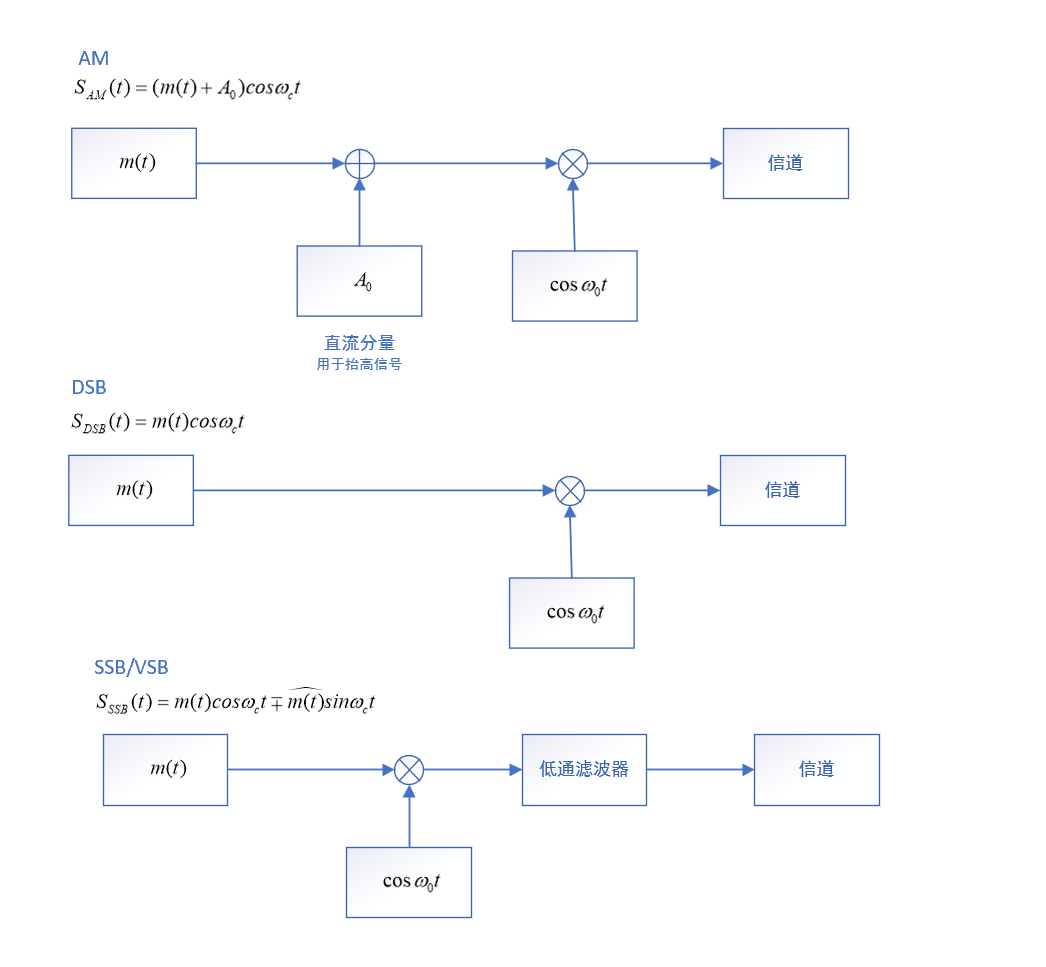
线性调制的方法分为：调幅（AM），双边带调制（DSB），单边带调制（SSB），残留边带调制（VSB）。这几种线性调制方法简图如下图所示：

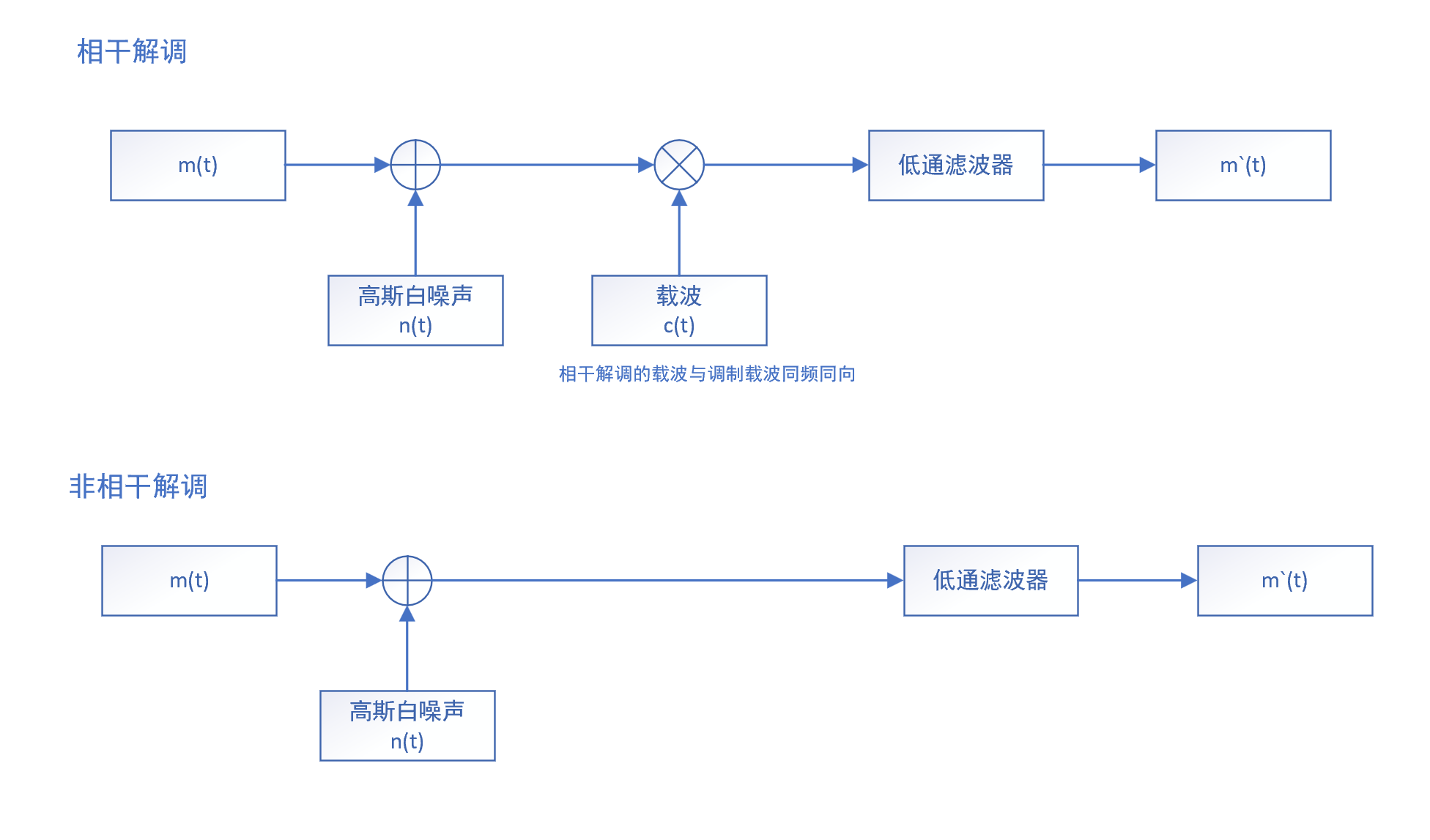
线性调制的解调方法分为两类：相干解调和非相干解调，两者的简图如下图所示：

调幅

标准调幅系统的框图如下。基带信号与一个直流信号叠加后进行抬升，然后以正弦波为载波通过乘法器。

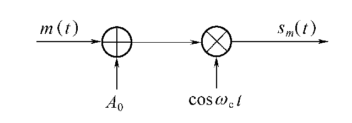
标准调幅可以用数学公式表达为：
\[S_{AM}(t)=[A_0+m(t)]cosω_ct\] 已调信号可以被分解为不含信息的载波项\(A_0cosω_ct\)和含有信息的边带项\(m(t)cosω_ct\)。
> 上述公式成立暗含着\(E(m(t))=0\)，即基带信号本身不含直流信号这一条件。

在时域上表现为正弦信号的包络线实则为经过抬升后的基带信号。
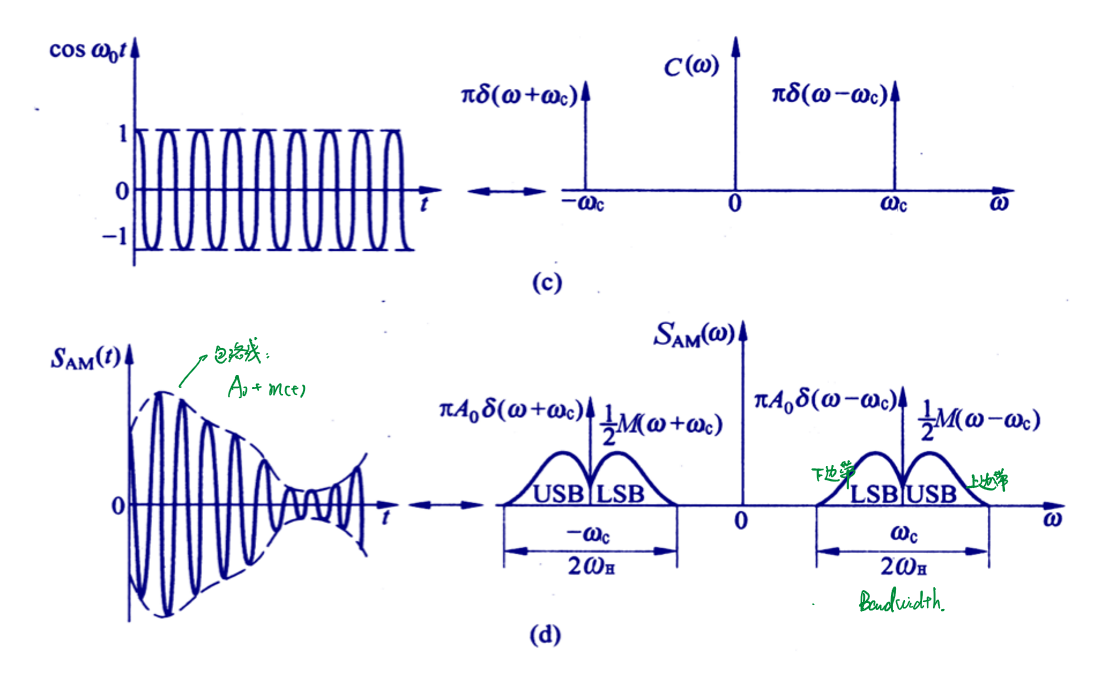
在频域中:
\[S_{AM}(ω)=πA_0[δ(ω+ω_c)+δ(ω-ω_c)]+\frac{1}{2}[M(ω+ω_c)+M(ω-ω_c)]\] 其在频谱图上表示为两段对称的连续频谱和两个冲击频谱。

调幅后的信号参数

带宽

由频谱可以看出,AM信号的频谱由载频分量、上边带（USB）、下边带(LSB)三部分组成。上边带的频谱结构与原调制信号的频谱结构相同,下边带是上边带的镜像。因此,AM信号是带有载波分量的双边带信号,它的带宽是基带信号带宽\(f_H\)的2倍,即:
\[B_{AM}=2f_H\]

能量·调制效率

已调信号的平均功率可以表示为：
\[P_{AM}=\overline{S^2_{AM}}=\overline{A_0^2cos^2ω_ct}+\overline{m^2(t)cos^2ω_ct}+\overline{2A_0m(t)cos^2ω_0t}\] 经过化简可以得到：
\[P_{AM}=\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}\] 其中载波功率：\(P_c=\frac{A_0^2}{2}\)，边带功率：\(P_s=\frac{\overline{m^2(t)}}{2}\)
即调制后信号的平均功率为载波功率和边带功率之和。
由于载波不携带任何信息，定义调制效率为边带功率与总功率之比以反映调制时信息的占比：
\[η_{AM}=\frac{P_s}{P_s+P_c}\]

调幅指数

由于对标准调幅的解调实质上是求得其包络线函数，在波形图上观察，当\(m(t)<A_0\)时，波形图的上下包络线会发生重叠从而无法还原之前的包络线函数，导致失真。

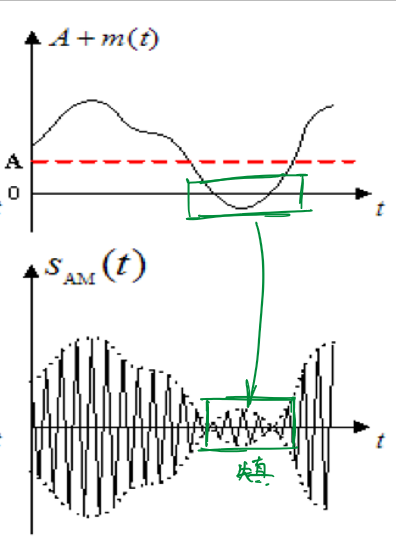
因此要求:
\[|m(t)|_{max}≤A_0\] 定义调幅指数\(β_{AM}\)反映\(|m(t)|_{max}\)与\(A_0\)的关系：
\[β_{AM}=\frac{|m(t)|_{max}}{A_0}\] - \(β_{AM}<1\)： 正常调幅 - \(β_{AM}=1\)： 满调幅 - \(β_{AM}>1\)： 过调幅

当然\(A_0\)并不是越大越好，倘若\(A_0\)设置的过大，那么会导致信息含量下降，调幅效率降低。

随机信号的调幅

当\(m(t)\)是一个高斯随机过程时，容易求得调幅过程的自相关函数：
\[R_{AM}=E[S_{AM}(t)S_{AM}(t+τ)]\] 其频谱仍然为：
\[P_{AM}(ω)=πA_0[δ(ω+ω_c)+δ(ω-ω_c)]+\frac{1}{2}[P_S(ω+ω_c)+P_S(ω-ω_c)]\] 对其进行积分，求得平均功率，可以发现上述有关平均功率的结论依然适用。

双边带调制(DSB)

对于调幅，其调制效率的最大值在受调信号\(m(t)\)达到最大值\(|m(t)|_{max}=A_m\)时取得，此时的最大调制效率为：
\[η_{AM}=\frac{\frac{A_m^2}{2}}{A_0^2+\frac{A^2_m}{2}}=\frac{1}{3}\] 可以发现，\(A_0\)虽然抬高了受调信号，但是调制效率非常低下。
双边带调制改进了调幅办法，取消了用于抬高的直流信号\(A_0\)，其余部分与调幅相同，其调制过程框图如图所示：

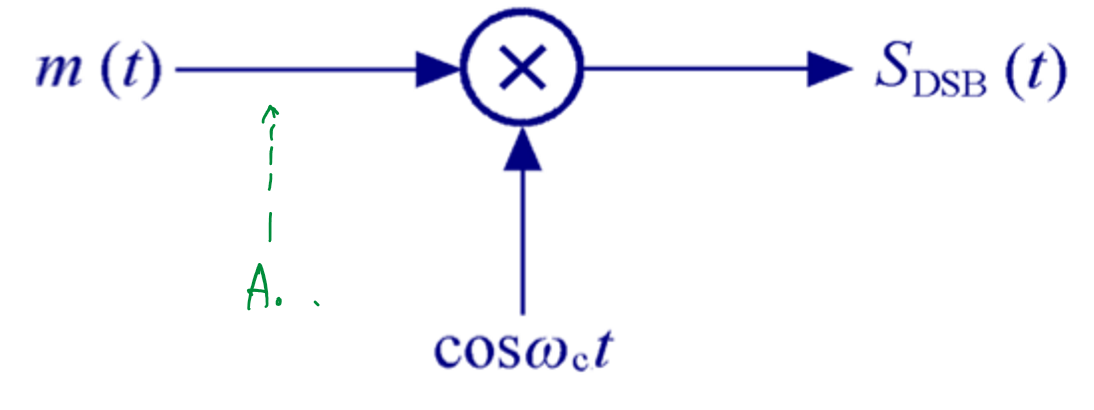
整个调制过程的输出信号\(S_{DSB}(t)\)可以表示为：
\[S_{DSB}(t)=m(t)cosω_ct\] 在频域上：
\[S_{DSB}(ω)=\frac{1}{2}[M(ω-ω_c)+M(ω+ω_c)]\] 其频谱分量中不再有冲击分量。

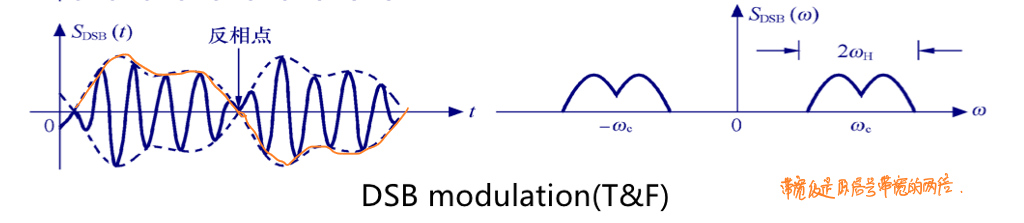
同调幅，其带宽仍然是原信号带宽的两倍。
\[B_{DSB}=B_{AM}=2f_H\] 由于去掉了\(A_0\)，双边带调制的能量为：
\[P_{DSB}=P_f=\frac{1}{2}\overline{m^2(t)}\] 最大调制效率为：
\[η_{max}=\frac{P_s}{P_c}=1\]

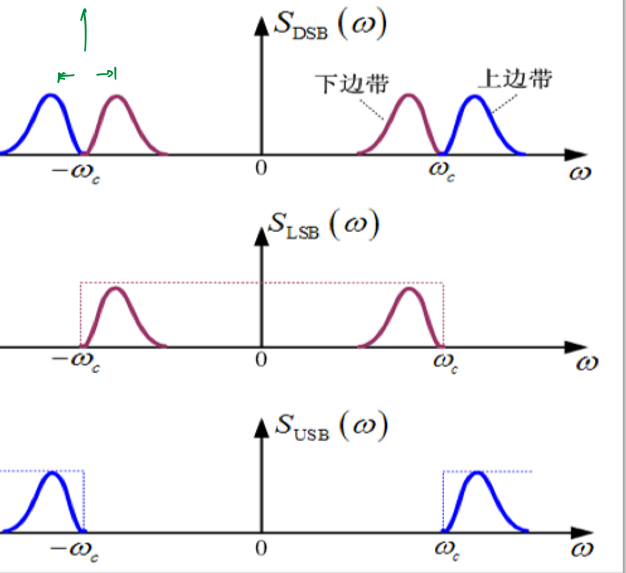
单边带调制(SSB)

调制过程的有效性用带宽利用率进行衡量，双边带调制的带宽比较大，因此其带宽利用率较低。同时通过对双边带调制结果的频谱分析，可以发现每个频谱成分中的半个边带（称为上边带/下边带）已经携带了受调信号的所有信息，因此考虑使用滤波器或者数学方法使得调制结果只包含单边带，以提高带宽利用率。这样的调制方法称为单边带调制。

滤波法

滤波法使用一个滤波器\(H_{SSB}(ω)\)过滤出LSB或USB，其调制过程如图所示：

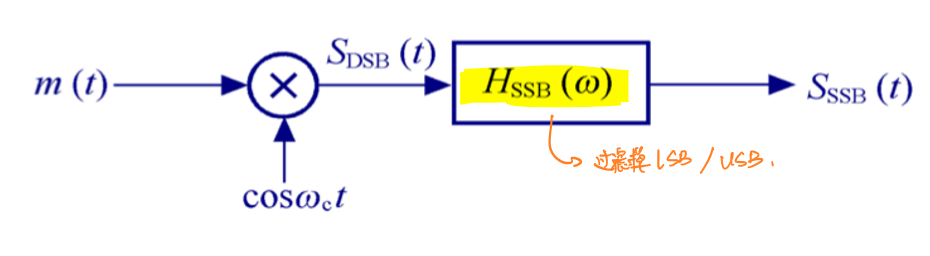
在实际运用中，由于LSB的峰值点和USB的峰值点非常接近，因此要求滤波器接近理想滤波情况，即要求滤波器在截止频率后的过滤频率剧烈变化。这样的滤波器设计在现实中是非常难实现的。

相移法

相移法通过数学上的希尔伯特变换使其能够将原信号变换为仅含有上边带或者下边带的部分。
对于正弦受调信号：\(m(t)=A_mcosω_mt\)，其受正弦双边带调制调制后的信号为：\(S_{DSB}(t)=m(t)c(t)=A_mcosω_mtcosω_ct\)。
利用积化和差公式可以得到：
\[S_{DSB}(t)=\frac{1}{2}cos(ω_c-ω_m)t+\frac{1}{2}A_mcos(ω_c+ω_m)t\]
其中加号连接的两项分别为上边带和下边带部分，因此下边带可以写作：
\[\begin{aligned} S_{LSB}(t)&=\frac{1}{2}cos(ω_c-ω_m)t\\ &=\frac{1}{2}A_mcosω_mtcosω_ct+\frac{1}{2}A_msinω_mtsinω_ct \\ &=\frac{1}{2}m(t)cosω_ct+\frac{1}{2}\hat{m(t)}sinω_ct \end{aligned}\] 可以发现\(sinω_mt\)实际上是\(cosω_mt\)通过 相移\(-\frac{π}{2}\)得来的。称将原信号\(m(t)\)在时域内相移\(-\frac{π}{2}\)的变换为希尔伯特变换，变换后的信号记为\(\hat{m(t)}\)。
> 希尔伯特变换表达式：\(\hat{f(t)}=f(t)*\frac{1}{πt}\)

同理，对上边带部分也有：
\[S_{USB}(t)=\frac{1}{2}m(t)cosω_ct-\frac{1}{2}\hat{m(t)}sinω_ct\] 因此相移法的调制结果可以表示为：
\[S_{SSB}=\frac{1}{2}m(t)cosω_ct ∓ \frac{1}{2}\hat{m(t)}sinω_ct\] > 注意上边带为“-”，下边带为“+”

无论哪一种调制方式，SSB结果的带宽都是DSB的一半：
\[B_{SSB}=\frac{1}{2}B_{DSB}=f_H\] SSB调制后的能量可以表示为：
\[P_{SSB}=\frac{1}{2}\overline{\frac{1}{2}m^2(t)cos^2ω_ct}+\frac{1}{2}\overline{\frac{1}{2}\hat{m^2(t)}sin^2ω_ct}=\frac{1}{4}\overline{m^2(t)}\]

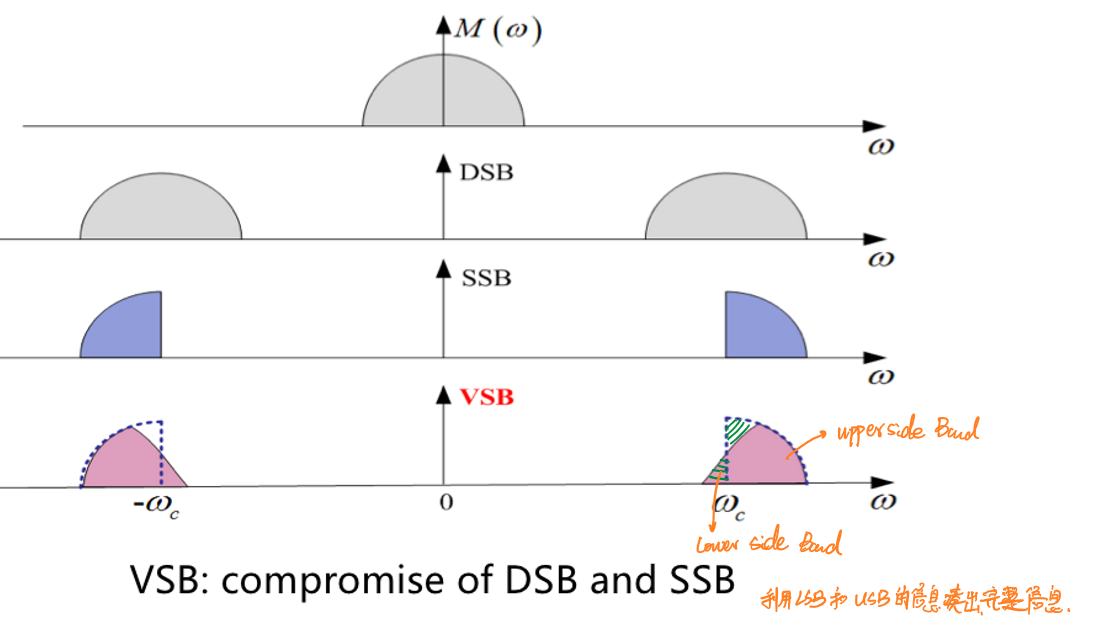
残留边带调制（VSB）

残留边带调制VSB在双边带调制的基础上，通过设计滤波器，使信号一个边带的频谱成分原则上保留，另一个边带频谱成分只保留小部分（残留）。该调制方法既比双边带调制节省频谱，又比单边带易于解调。
可以理解为VSB利用过滤后残留的上边带和下边带部分拼凑出一个完整的信息。

线性调制过程的噪声

由于所有的调制过程都是线性调制，而本课内默认所有噪声为高斯白噪声，根据平稳高斯随机过程通过线性系统的特点，可以得出线性调制过后的噪声应该和基带信号中的加性噪声能量相等：
\[N_{modulation}=N_{baseband}=n_0B\] 其中\(n_0\)表示噪声的功率谱密度，\(B\)表示调制后噪声的带宽。

信道衰减·输入信噪比

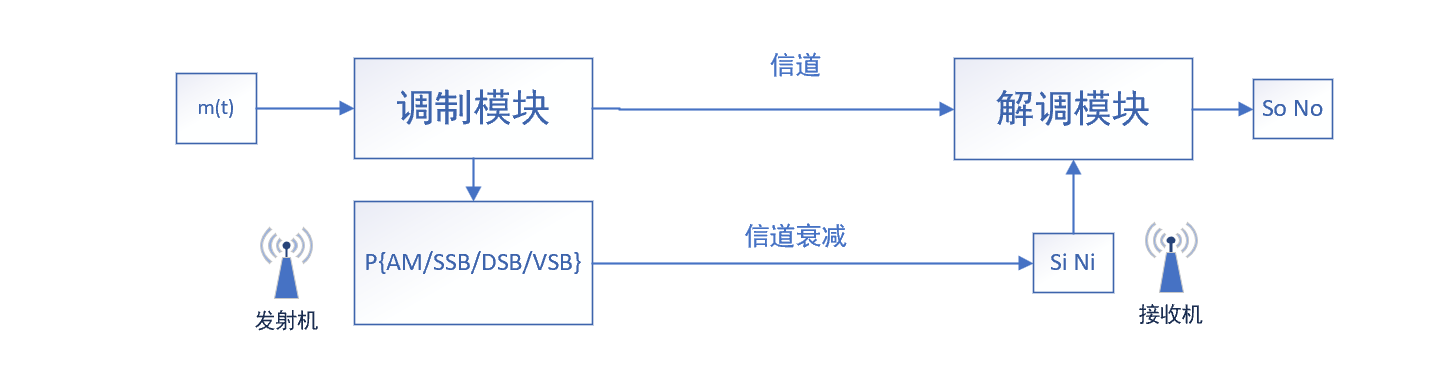
经过线性调制后的信号通过发射机(TX)发送，进入信道，在信道中由于干扰和噪声，导致信号功率出现损失，使得接收机(RX)接收的信号功率与发射机发射的信号功率不同，定义信道中的衰减（ATU）为发射机发射功率与接收机接收功率之比：
\[ATU|dB=10lg\frac{P_{TX}}{P_{RX}}\] 因此，在解调模块处，接收机接收到的功率可以表示为：
\[P_{TX}=P_{RX} × ATU=P_{AM/DSB/SSB}\] 在这个过程中，假设噪声通过信道时不会发生任何改变，噪声的功率仍然与基带信号中的噪声功率相同。

定义输入信噪比(\(SNR_i\))为输入进解调模块的信噪比：
\[SNR_i=\frac{S_i}{N_i}\] 其中，\(S_i=P_{RX}=P_{AM/DSB/SSB} / ATU\)。
\(N_i=N_{modulation}=n_0B\)。

总结：线性调制方法的性质

线性调制方法	输出表达式	带宽	调制后功率\(P_{TX}\)	调制端噪声	无衰减下的输入信噪比\(SNR_i\)
调幅(AM)	\(S_{AM}=(A_0+m(t))cosω_ct\)	\(2f_H\)	\(\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}\)	\(2n_0f_H\)	\(\frac{A_o^2+\overline{m^2(t)}}{4n_0f_H}\)
双边带调制(DSB)	\(S_{DSB}=m(t)cosω_ct\)	\(2f_H\)	\(\frac{\overline{m^2(t)}}{2}\)	\(2n_0f_H\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)
单边带调制(SSB) 残留边带调制(VSB)	\(S_{SSB}=\frac{1}{2} m(t)cosω_ct∓\frac{1}{2}\hat{m(t)}sinω_ct\) \(\hat{m(t)}\) 表示\(m(t)\) 相移 \(-\frac{π}{2}\) 的结果 即希尔伯特变换 保留上边带为“-”，下边带为“+”	\(f_H\)	\(\frac{\overline{m^2(t)}}{4}\)	\(n_0f_H\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)