数字信号处理-知识点总结

离散信号和系统的性质

线性

对于系统\(H\)，有\(y_1[n]=H[x_1[n]]\),\(y_2[n]=H[x_2[n]]\)，如果： \[H[A_1x_1[n]+A_2x_2[n]]=A_1y_1[n]+A_2y_2[n]\] 称系统是线性的。

时不变

对于系统\(H\)，有\(y[n]=H[x[n]]\)，如果：
\[H[x[n-τ]]=y[n-τ]\] 称系统是时不变的。

稳定

对于系统\(H\)，如果系统输入有界\(x[n]<∞\)，系统输出\(y[n]<∞\)，称系统是稳定的。

因果

对于系统\(H\)，如果系统输出\(y[n]\)不与未来系统的输入\(x[n+m],m∈Z^*\)有关，称系统是因果的。

周期性

如果序列满足：
\[x[n+N]=x[n]\] 那么序列是周期的。
对于正弦序列\(x[n]=Acos(\omega_0n+φ)\)，如果： \[N=\frac{2πk}{ω_0},k=0,1,2...,N-1\] 能找到\(k\)使得\(N\)是一个整数，那么这个正弦序列是周期的。

共轭对称和共轭反对称

对于某个序列中的每一项\(x[n]\)可以拆解为实部和虚部的形式：\(x[n]=x_r[n]+jx_i[n]\): 如果另一个序列的每一项满足： \[x_e^*[n]=x_r[n]-jx_i[n]\] 称序列\(x_e^*[n]\)是序列\(x[n]\)的共轭对称序列。

如果另一个序列\(x_o^*[n]\)的每一项满足：

\[x_o^*[n]=-(x_r[n]-jx_i[n])\]

称序列\(x_o^*[n]\)是序列\(x[n]\)的共轭反对称序列。

离散时间域分析方法

离散时间傅里叶变换

一个信号可以被分解为系数与本征函数的线性组合:
\[x[n]=∑w[n]E[n]\] 其中\(E[n]\)为本征函数。
离散时间傅里叶变换（DTFT）的物理意义是一个离散序列\(x[n]\)可以表示为无数个指数序列的线性组合，这个线性组合的系数为其离散时间傅里叶变换的结果：
\[x[n]=\frac{1}{2π}∫_{-π}^πX(e^{jω})e^{jωn}dω\] \[X(e^{jω})=∑x[n]e^{-jωn}\]

直接计算离散时间傅里叶变换的两种方法：
- 递推法，适用于出现系统反馈\(y[n-m]\)时。
- 通项定义法，根据定义写出通项表达式，使用等比数列求和后用欧拉公式进行化简。

线性卷积

两个序列的线性卷积表示为：
\[x[n]*y[n]=∑_{m}x[m]y[m-n]\] 当其中一个输入为\(x[n]=e^{jωn}\)时，线性卷积的结果是另一个输入的离散时间傅里叶变化结果\(Y(e^{jω})\)。

线性卷积的时域计算方法

时域计算两个有限长度序列的线性卷积的方法为不进位乘法，方法为：
两个序列的末尾（最右边）对齐，做竖式乘法，其每一位的结果不进位，得到线性卷积后的结果。
结果中\(n=0\)一项的位置由第一个序列中最右边距离\(n=0\)的位置\(N_1\)与第二个序列中最右边距离\(n=0\)的位置\(N_2\)确定，结果中\(n=0\)一项的位置为从右往左数第\(N_1+N_2-1\)项。

Z变换

\[X_r(e^{jω})=∑x[n]r^{-n}e^{-jωn}=∑x[n](re^{jω})^{-n}\] 将：\(re^{jω}\)简记为\(z\)，得到Z变换的变换公式：
\[X(z)=∑x[n]z^{-n}\] 常用的两个序列的Z变换：
\[δ[n]↔1,Aδ[n-n_0]↔Az^{-n_0}\] \[a(b)^nu[n]↔\frac{a}{z-b}\]

Z变换的收敛域

Z反变换的结果会根据Z变换收敛域的不同而不同。序列特征和对应Z变换的收敛域如下表所示：

序列类型	收敛域	图示
右边序列：\(x[n]=a^nu[n]\)	\(‖z‖>‖a‖\)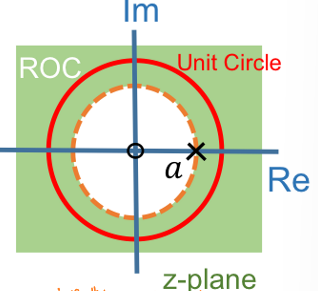
左边序列：\(x[n]=-a^nu[-n-1]\)	\(‖z‖<‖a‖\)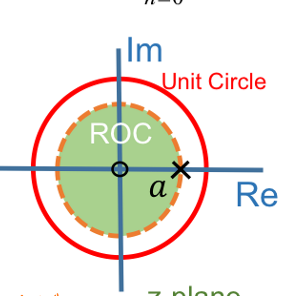
双边序列:\(x[n]=a^nu[n]-b^nu[-n-1]\)	\(‖a‖<‖z‖<‖b‖\)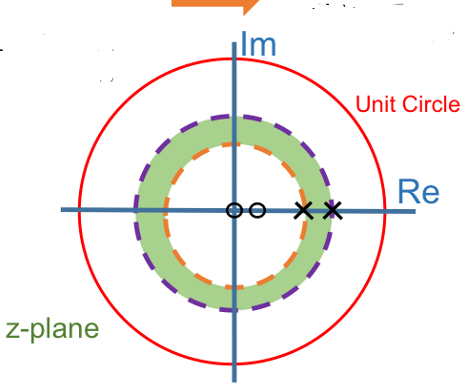

收敛域对应系统的性质：
- 右边序列对应系统因果。 - 系统稳定时，收敛域应当包括单位圆。

Z反变换

通常，Z反变换使用部分分式法来求解，基本步骤是：
1. 对分母做因式分解，找到极点。
2. 根据因式分解结果将整个式子拆分为多个分数相加的形式，并找到零点。
3. 进行反变换。

反变换时需要根据\(z-a_i\)的正负对Z变换的收敛域进行讨论:
- 当\(|z|<(a_i)_{min}\)时，根据极点对应序列形式（收敛特性一小节中提到的表格），该项对应的指数序列为左边序列\(-A_i(a_i)^nu[-n-1]\)。 - 当\(|z|>(a_i)_{max}\)时，根据极点对应序列形式，该项对应的指数序列为右边序列\(A_i(a_i)^nu[n]\)。 - 当\(a_{min}<|z|<a_{max}\)时，根据极点对应序列形式，该项对应的指数序列为双边序列。

需要注意左边序列每一项前面的符号为负：\(-A_i(a_i)^nu[-n-1]\)

离散傅里叶变换/离散傅里叶级数

N点离散傅里叶变换定义为：
\[X[k]=∑_{n=0}^{N-1}x[n]e^{-j\frac{2π}{N}kn}\] 反变换为：
\[x[n]=\frac{1}{N}∑_{k=0}^{N-1}X[k]e^{j\frac{2π}{N}kn},0≤n≤N-1\] 离散傅里叶级数则是当变换对象为周期序列\(\tilde{x}[n]\)时的离散傅里叶变换结果。相当于取周期序列\(\tilde{x}[n]\)的主值序列进行离散傅里叶变换后进行周期延拓。
计算时需要注意：
当\(N\)大于序列长度时，使用0对\(x[n]\)进行填充。
当\(N\)小于序列长度时则会发生混叠（Alising）。长度为\(L\)的序列\(x[n]\)发生混叠的过程表示为：
\[\begin{aligned} x[0],x[1],...,&x[N],...,x[L-2],x[L-1]\\ &⇓\\ x[0]+x[N],x[1]+&x[N+1],...,x[N-1]+x[2N-1] \end{aligned}\] 简单来说就是把超出\(N\)的序列部分截断，与原序列从\(x[0]\)开始对位叠加。

直接计算离散傅里叶变换的两种方法：
- 递推法，适用于出现系统反馈时。
- 通项定义法，根据定义写出通项表达式，使用等比数列求和后用欧拉公式进行化简。

离散傅里叶变换计算中可能会用到的重要公式：
- 等比数列求和公式：
对于公比为\(q\),长度为\(n\)的等比数列，其和为：
\[\frac{a_1(1-q^n)}{1-q}\] - 欧拉公式：
\[cosx=\frac{1}{2}(e^{-jx}+e^{jx})\] \[sinx=\frac{1}{2j}(e^{jx}-e^{-jx})\]

\(x[n]=e^{jω_0n}\)具有周期性：
\[x[n]=e^{jω_0n}=e^{j(ω_0+2πk)n}=x[n+N]\] 复指数序列\(x[n]\)具有周期性，称\(N\)为其周期。

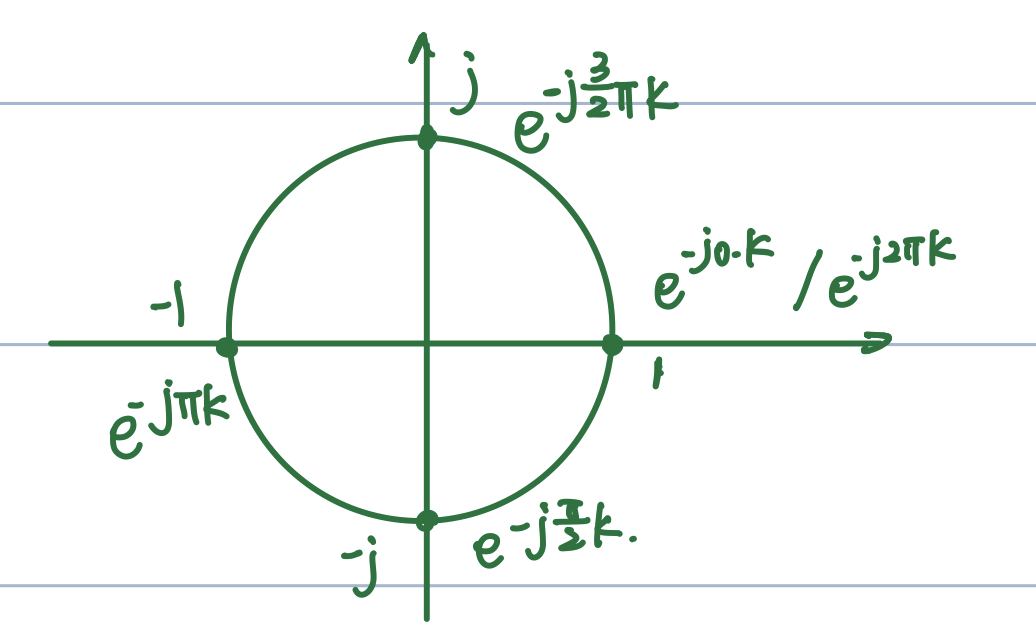
循环移位

\(x[n]\)的N点左移\(m\)的循环移位结果为\(x[(n+m)modN]\)。
\((n+m)modN\)运算的含义是取序列的\(0-N\)部分以\(N\)为周期进行延拓，延拓后的序列向左平移\(m\)个单位，取现在序列\(0-N\)的结果。

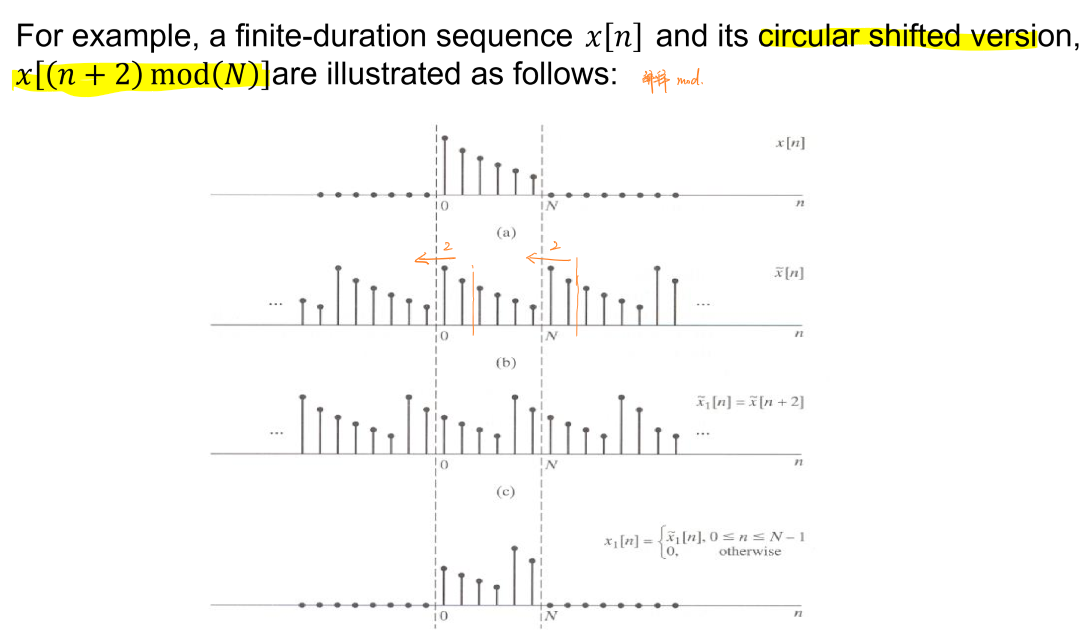
循环卷积和周期卷积

定义两个序列非周期序列的\(N\)点\(x[n]\)、\(y[n]\)循环卷积/圆周卷积（Circular shift）为：
\[x[n]⊗_Ny[n]=∑_{m=0}^{N-1}x[m]y[(n-m)mod(N)]\] 同样地，当\(N\)大于两个序列的长度时，直接将两个序列的长度用0填充到长度\(N\)，再进行循环卷积。
当\(N\)小于两个序列的长度时，循环卷积时则会发生混叠。
\(x[n]\)和\(y[n]\)具有相同的序列长度，两个序列长度如果不相同，使用0进行补齐。
其物理意义是将其中一个序列反转（称为反褶）后，进行\(N\)点循环时移\(m\)次，与原序列线性卷积的结果。

在频域上，循环卷积对应两个序列DFT的乘积：
\[x[n]⊗y[n]↔X[k]Y[k]\]

圆周卷积的时域计算方法

圆周卷积在时域上可以通过矩阵快速计算：
\[x[n]⊗y[n]=\left[\begin{matrix} z[0] \\ z[1] \\ ...\\ z[N-2] \\ z[N-1] \end{matrix}\right]=\left[\begin{matrix} y[0] & y[N-1] & ...& y[2] & y[1]\\ y[1] & y[0] & ...& y[3] & y[2]\\ ...&...&...&...&...\\ y[N-2] & y[N-1] & ...& y[0] & y[N-1]\\ y[N-1] & y[N-2] & ...& y[1] & y[0]\\ \end{matrix}\right]\left[\begin{matrix} x[0] \\ x[1] \\ ...\\ x[N-2] \\ x[N-1] \end{matrix}\right]\] 可以发现矩阵\(Y\)内部每一列的元素在进行周期性的位置轮换。

周期卷积则是将两个同周期的周期序列\(\tilde{x_1}[n]\)、\(\tilde{x_2}[n]\)的主值序列进行循环卷积后进行周期延拓的计算。

离散时间傅里叶变换、Z变换、离散傅里叶变换的关系

周期序列\(\tilde{x}[n]\)做傅里叶级数分析后一周期内（\(0≤n≤N-1\)）的结果与\(x[n]\)做离散傅里叶变换的结果完全一致。

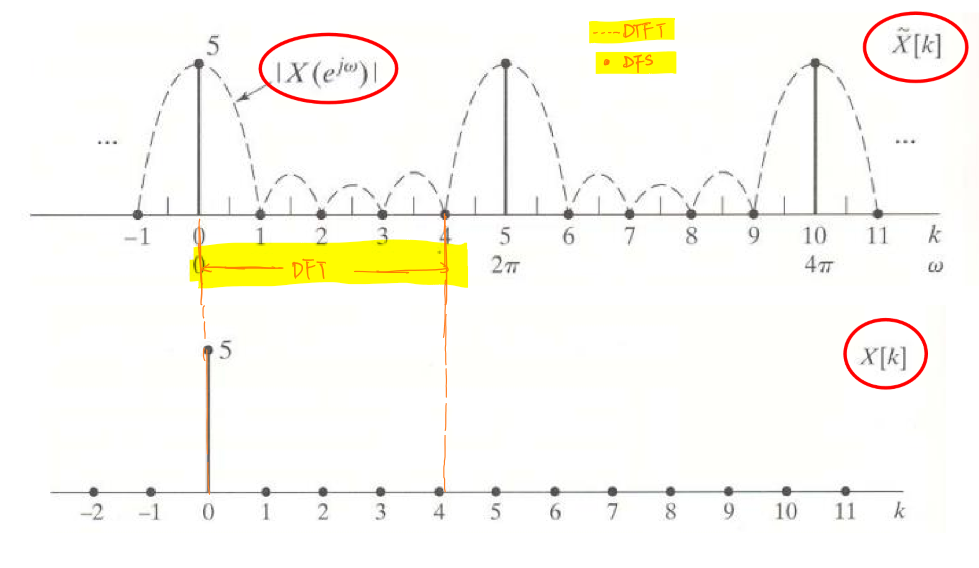
可以发现：离散傅里叶级数是对离散时间傅里叶变换的结果进行采样，而一周期内的采样结果则为离散傅里叶变换的结果。
对于Z变换，\(z=re^{jω}\)，如果选择\(r=1\)，那么Z变换将退化为离散时间傅里叶变换：
\[X(e^{jω})=X(z)|_{z=e^{jω}}\] 因此，Z域单位圆上的任意一点表示\(e^{jω}\)。 而离散傅里叶变换是对离散时间傅里叶变换一周期内的采样，因此离散傅里叶变换是在Z域单位圆上的均匀采样。

线性卷积、循环卷积、周期卷积的关系

当循环卷积的点数大于\(2L-1\)（即线性卷积的长度）时，其结果与线性卷积（\(x[n]*y[n]\)）完全相同。
如果\(\tilde{x_1}[n]\)、\(\tilde{x_2}[n]\)分别对应是\(x_1[n]\)、\(x_2[n]\)以周期为\(N\)的延拓，有：
\[(x_1[n]⊗_Nx_2[n])R_N=\tilde{x_1}[n]\tilde{⊗}_N\tilde{x_2}[n]\] \(R_N\)表示以周期为\(N\)的延拓。
即在周期卷积对象的主值序列是循环卷积对象时，\(N\)点循环卷积是\(N\)点周期卷积的主值序列。

快速傅里叶变换

快速傅里叶变换是计算离散傅里叶变换的一种近似计算方式。只有在序列长度为\(2^n\)时才能够使用。
快速傅里叶变换的结构基于蝶形运算：

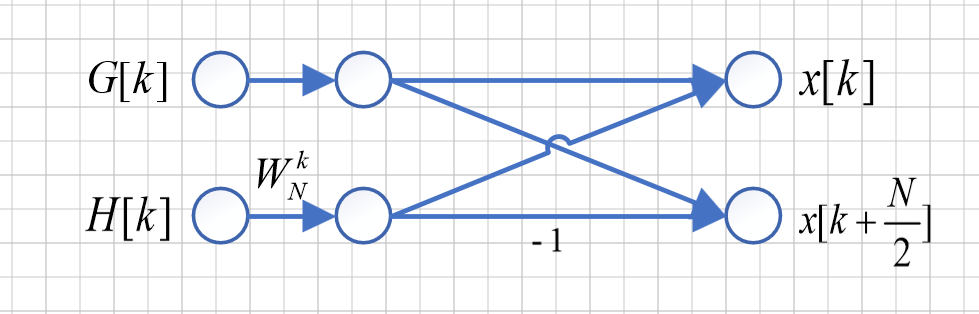
对于\(N=2^m\)，需要\(m\)级次蝶形结构的运算。

快速傅里叶变换的步骤是：
1. 做比特镜像反转，即1点FFT。
2. 对\(i\)级，其\(x[n]\)和\(x[n+i]\)配对，使用蝶形结构进行运算。
3. 重复上述过程，直到达到对应的级，完成\(N\)点FFT的计算。

如果序列长度为\(N\)，其计算量为：
\[N+\frac{N}{2}log_2N\] 一个8点快速傅里叶变换结构如下图所示：

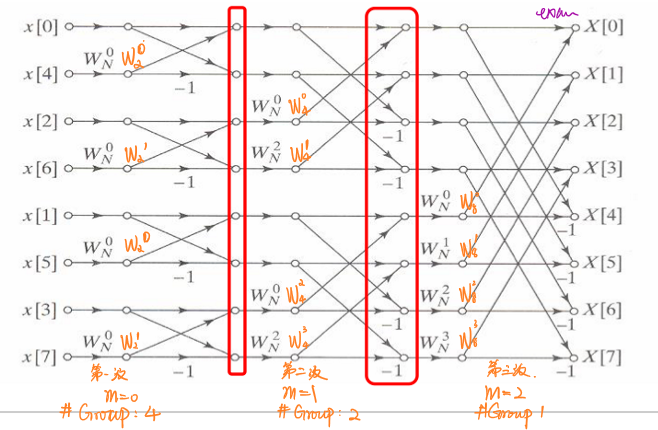
系统的表示方法

对于一个离散系统，其差分方程为：
\[∑_{k=0}^Na_ky[n-k]=∑_{k=0}^Mb_kx[n-k],a_0≠0,b_0≠0\]

系统的单位采样响应/系统的冲激响应

系统的单位采样响应指输入为\(δ[n]\)时候的系统输出\(h[n]\)。通常可以带入\(x[n]=δ[n]\)到差分方程递归运算得到。也可以通过对系统的频率响应求Z反变换得到。
系统输出可以表示为：
\[y[n]=x[n]*h[n]\]

系统的频率响应/转换方程

当系统的输入\(x[n]=e^{jωn}\)时：
\[y[n]=e^{jωn}∑h[k]e^{-jωk}\] \(∑h[k]e^{-jωk}\)正好对应其离散时间傅里叶变换\(H(e^{jω})\)，称为其频率响应。
频率响应可以通过观察差分方程快速写出：
\[H(e^{jω})=\frac{∑b_ke^{-jωk}}{∑a_ke^{-jωk}}\] 带入\(z=e^{jω}\)，得到其Z域下的表现称为转换方程：
\[H(z)=\frac{∑b_kz^{-k}}{∑a_kz^{-k}}\] 也可以通过对\(h[n]\)求离散时间傅里叶变换得到。
由于Z域的收敛域可以不同，一个转换方程/差分方程可以对应多个冲激响应。但是只有当系统因果时，才能具备离散时间傅里叶变换的条件。
因此，只有系统的冲激响应\(h[n]\)和系统的频率响应\(H(e^{jω})\)可以确定唯一的系统。

系统的幅频响应和相频响应

系统的频率响应也可以写作：
\[H(e^{jω})=|H(e^{jω})|e^{-j∠H(e^{jω})}\] \(|H(e^{jω})|\)是系统的幅度值-频率响应（Magnitude-frequency response）简称幅频响应或者幅度值响应。\(∠H(e^{jω})\)是系统的相位-频率响应，简称相频响应或相位响应。
系统的幅度相应和相位响应的求法为：
将系统频率响应改为对应的Z域方程，找到系统的零点和极点，在Z域上作图。然后连接单位圆上的任意一点，求解零点/极点与该点构成向量（称为零向量和极向量）的模和角度。

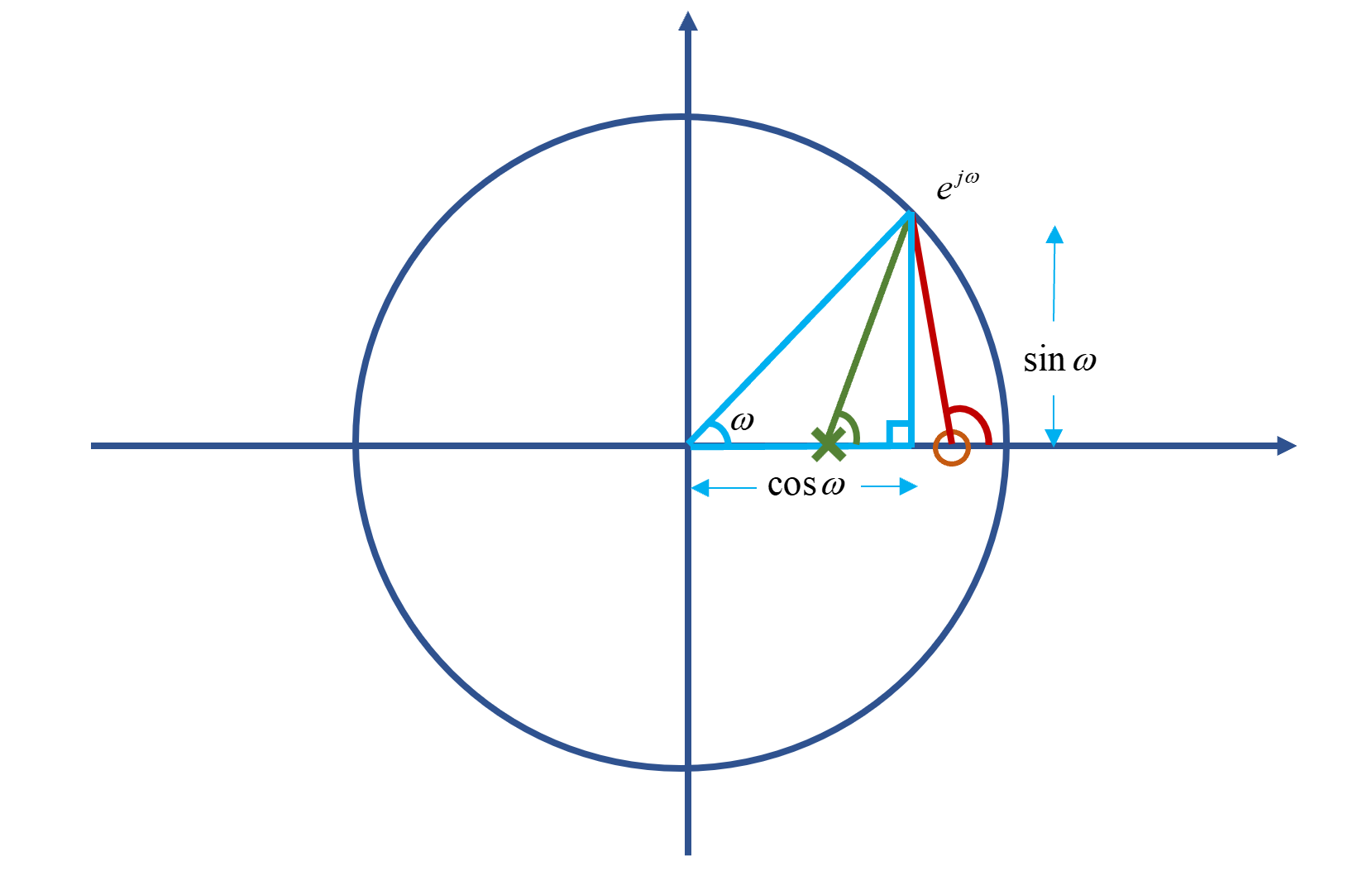
• 系统方程的模长/幅度值(Magnitude)：
  \[|H(e^{jω})|=\frac{Π零向量的模长}{Π极向量的模长}\] 即系统方程频率响应\(H(e^{jω})\)的幅度值-频率响应，简称幅频响应。
  
• 系统方程的相位：
  \[∠H(e^{jω})=∑零向量的角度-∑极向量的角度\] 即系统方程频率响应\(H(e^{jω})\)的相位-频率响应，简称相频响应。

正弦信号通过系统
如果正弦信号为\(Acos(ω_0t+θ_0)\)，通过系统\(H(e^{jω})=|H(e^{jω})|e^{-j∠H(e^{jω})}\)后的表达式为：
\[A|H(e^{jω_0})|cos(ω_0t+θ_0+∠H(e^{jω_0}))\]

FIR系统和IIR系统

对Z域转换方程做Z反变换：
\[h[n]=∑_{r=0}^{M-N}B_rδ[n-r]+∑_{k=1}^NA_k(d_k)^nu[n]\] 由于\(u[n]\)是一个无限长度的序列，因此系统的冲激响应也是无限长度的，称这样的系统为无限冲激响应系统（IIR System）。
当\(N=0\)时，差分方程左边只含有\(y[n]\)，系统方程的当前输出只由输入\(x\)决定，系统不含有反馈，此时系统方程为：
\[h[n]=∑_{r=0}^{M}B_rδ[n-r]\] 由于\(δ[n-r]\)长度有限，整个系统的冲激响应的长度是有限的，称这样的系统为有限冲激响应系统（FIR System）。

	N	差分方程左侧	有无反馈	冲激响应长度
IIR	N>0	含有\(y[n-k]\)	有	无限
FIR	N=0	只有\(y[n]\)	无	有限

滤波器设计

滤波器的理论结构

对于FIR滤波器，滤波器的理论结构如下表所示：

类型	基于的系统表示	图示
直接型	\(y[n]=∑_kh[k]x[n-k]\)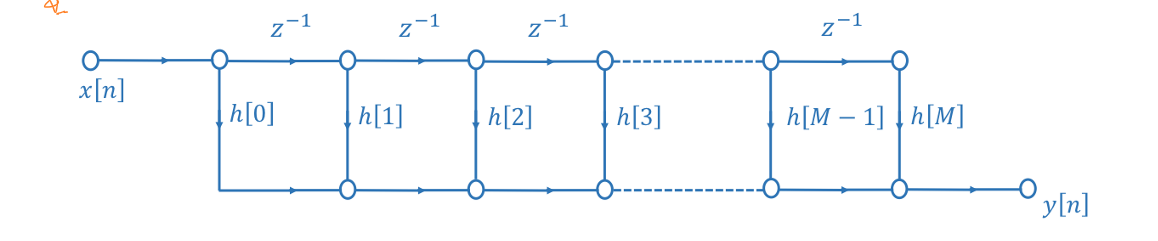
级联型	\(Y(z)=G∏_{k=1}^{M_s}(b_{0k}+b_{1k}z^{-1}+b_{2k}z^{-2})X(z)\)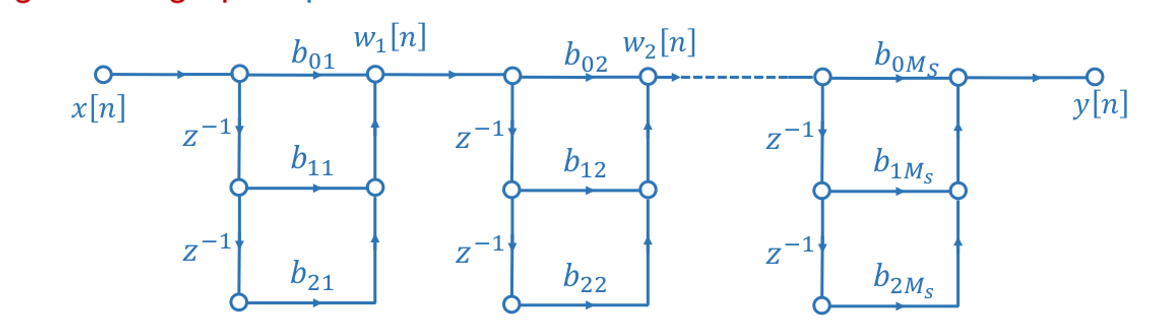

对于IIR滤波器，滤波器的理论结构类型如下表所示：

类型	基于的系统表示	图示
直接型	\(y[n]=v[n]+∑_{k=1}^Na_ky[n-k]\) \(v[n]=∑_{k=0}^Mb_kx[n-k]\)
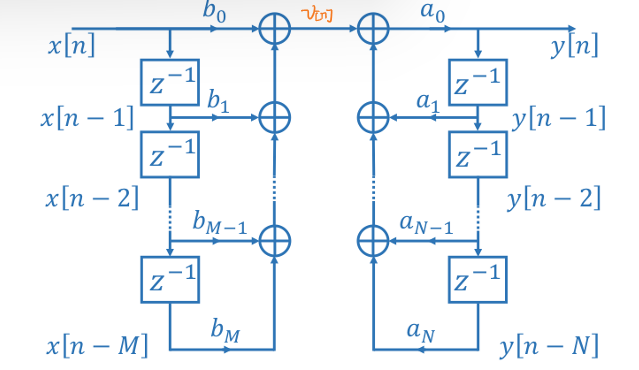标准型	\(H(Z)=\frac{Y(Z)}{W(Z)}\frac{W(Z)}{X(Z)}\) \(x[n]=∑_iA_iw[n-i]\) \(y[n]=∑_iB_iw[n-i]\)
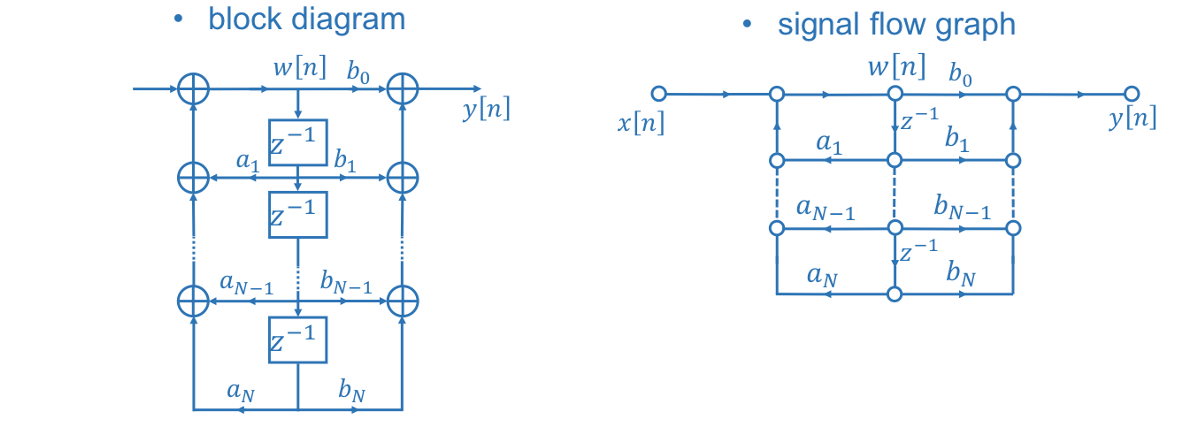级联型	\(H(z)=G∏_{k=1}^{N_s}\frac{(z_k-z^{-i})}{(p_k-z^{-i})}=G∏_{k=1}^{N_s}H_i(z)\)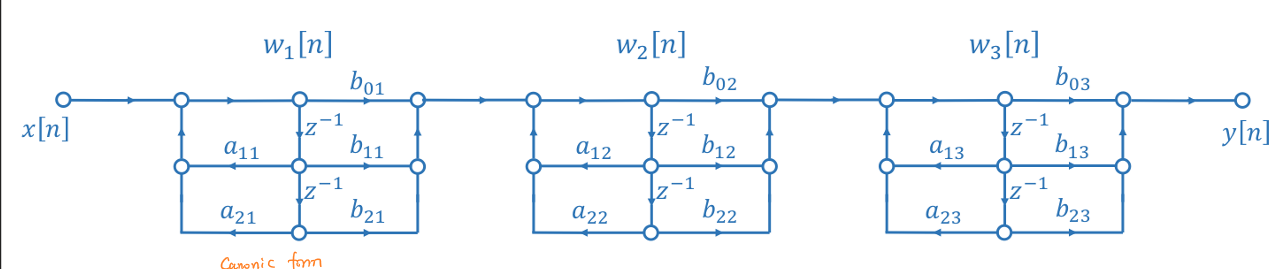
并联型	\(H(z)=∑_{k=0}^{N_p}C_kz^{-k}+∑_{k=1}^{N_s}\frac{e_{0k}+e_{1k}z^{-1}}{1-a_{1k}z^{-1}-a_{2k}z^{-2}}\)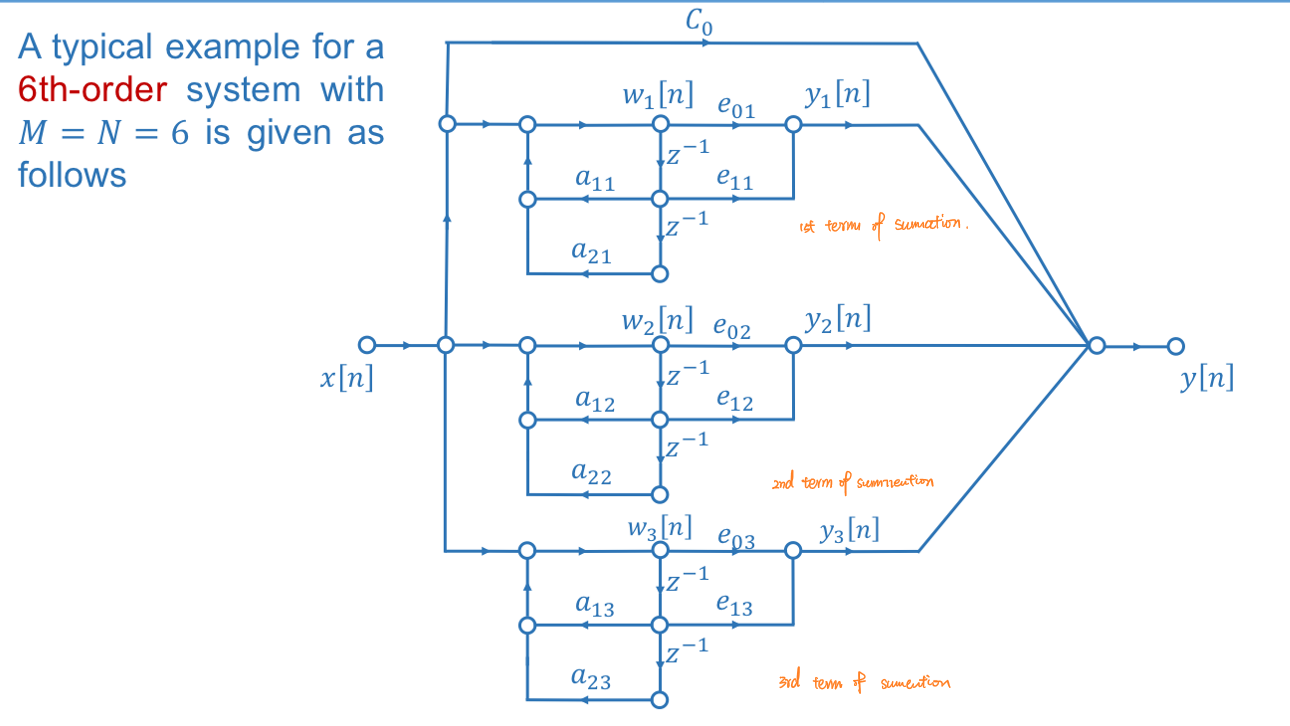

FIR滤波器设计的加窗法

加窗法的实现依赖于理想低通滤波器，理想低通滤波器的冲激响应为：
\[h[n]=\frac{sin(ω_cn)}{πn}\] 其中\(ω_c\)表示其截止频率。
1. 设置滤波器的长度\(L=2N+1\)，并在理想低通滤波器冲激响应上截取\(L\)个采样点。为了满足线性相位滤波器的条件，通常使用以\(h[0]\)为对称轴的奇数\(L\)个序列。定义滤波器的阶数\(M\)为滤波器序列长度减一： \[M=L-1\] 此时的序列为\(\{h[-N],h[-N+1],..,\underset{n=0}{h[0]},..,h[N-1],h[N]\}\),是一个非因果序列。 2. 对截取的序列做时移以满足系统的因果性，时移量为\(α=\frac{L-1}{2}\)，称为滤波器的群时延(Group delay)。
此时的序列为：\(\{\underset{n=0}{h[-N]},h[-N+1],..,h[0],..,h[N-1],h[N]\}\) 3. 为了使得滤波器性能更好，还需要对产生的序列进行赋权，产生赋权序列的函数称为窗函数（Window function），赋权的操作为： \[fl[n]=h_d[n]×w[n]\] 其中\(h_d[n]\)为截取和时移之后的理想低通滤波器序列，\(w[n]\)由窗函数产生。

需要注意的是，窗函数的阶数比序列阶数高2，再截掉窗函数序列两端的0后，与理想低通滤波器序列相乘。

窗函数

窗函数类型	表达式	\(e_p=20lgδ\)	过渡带带宽
三角窗	\(\begin{cases}\frac{2}{M}n,0≤n≤\frac{M}{2}\\ 2-\frac{2}{M}n,\frac{M}{2}≤n≤M \end{cases}\)	-25	\(\frac{2.37π}{M}\)
汉宁窗	\(0.5-0.5cos(\frac{2πn}{M})\)	-44	\(\frac{5.01π}{M}\)
海明窗	\(0.54-0.46cos(\frac{2πn}{M})\)	-53	\(\frac{6.27π}{M}\)
布莱克曼窗	\(0.42-0.5cos(\frac{2πn}{M})+0.08cos(\frac{4πn}{M})\)	-74	\(\frac{9.19π}{M}\)

IIR滤波器设计

模拟滤波器

定义其通带波纹\(R_p\)为：
\[R_p|_{dB}=-10lg|H_a(jΩ_p)|^2=-10lg\frac{1}{1+ϵ^2}\] 止带衰减\(A_s\)为：
\[A_s=-10lg|H_a(jΩ_s)|^2=-10lg\frac{1}{A^2}\]

模拟滤波器类型

• 巴特沃斯滤波器
  巴特沃斯滤波器的频率响应：
  \[|H(e^{jω})|^2=\frac{1}{1+(\frac{Ω}{Ω_c})^{2N}}\]

• 切比雪夫滤波器
  切比雪夫I型滤波器的频率响应：
  \[|H(e^{jω})|^2=\frac{1}{1+ϵ^2T_N^2(\frac{Ω}{Ω_c})}\] \(T_N(x)\)为N阶切比雪夫多项式：
  \[T_N(x)=\begin{cases} cos(Narccos(x)),0≤x≤1\\ cosh(Narccosh(x)),1≤x≤∞ \end{cases}\] > \(cosh(x)=\frac{e^x+e^{-x}}{2}\)

  \[ϵ=\sqrt{10^{0.1R_p}-1}\]

模数转换-冲激响应不变

脉冲响应不变的映射律：
\[h[n]=Th_c(nT)\] 脉冲响应不变法的流程：
1. 根据设计要求的通带截止频率和止带截止频率将数字角频率还原为模拟角频率：\(Ω_p=\frac{ω_p}{T},Ω_s=\frac{ω_s}{T}\)。
2. 设计出对应的模拟滤波器。
3. 求出模拟滤波器的频率响应：\(H_c(s)=∑_{k=1}^N\frac{A_k}{s-s_k}\)。 4. 根据映射律：\(H(z)=∑\frac{A_k}{1-e^{s_kT}z^{-1}}\)，得到数字滤波器的频率响应。

由于其所有的极点在s域以\(Ω_c\)为半径的圆上均匀分布，因此极点可以根据下图快速求得：

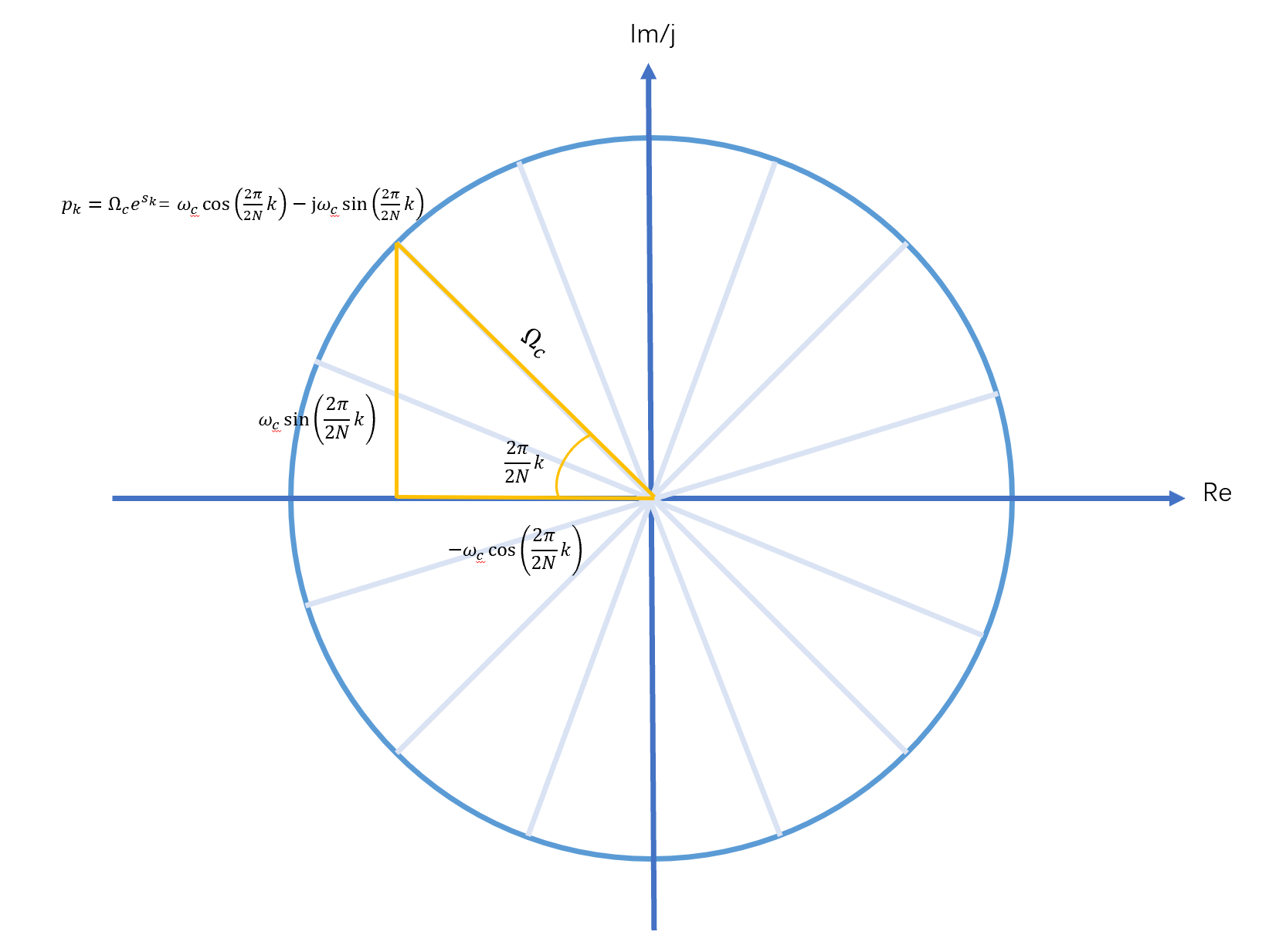
可以求得：
\[s_k=Ω_ccos(\frac{π}{N}k)-jΩ_csin(\frac{π}{N}k)\]

模数转换-双线性转换

双线性转换的映射律：
\[s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\] 其模拟角频率与数字角频率之间的关系是：
\[Ω=\frac{2}{T}tan\frac{ω}{2}\]

MATLAB程序设计基础

绘制频率响应

给定系统冲激响应\(h[n]\)下，绘制其频率响应需要注意的是：
- 需要对\(h[n]\)进行周期延拓，方法是使用zeros(1,L)创建一个长度为L的全0向量用x=[x,zeros(1,L)]对其填充。
- 使用fft()函数求其FFT结果。abs()求结果的绝对值得到幅频响应，angle()求FFT结果的相频响应。
- 横轴应当为[0:(N+L)]*2*pi/(N+L+1)使得0-2π内每一格的长度为\(\frac{2π}{N+L+1}\) （因为0:(N+L)有N+L+1个数）

下面的示例程序展示了如何绘制\(h[n]=Sa(0.1(n-50)),0≤n≤100\)的幅频和相频响应曲线：

N=100; %100点FFT
n=0:N;
x=sinc(0.1*(n-50));
x=[x,zeros(1,1000)]; %对x周期延拓到长度为1000
X=fft(x); %求其FFT/DFS结果（Amplitude Response）
subplot(2,1,1);
w=[0:(N+1000)]*2*pi/(N+1001);%横轴，每一格表示2π/(N+1001)
plot(w./pi,abs(X));  %取绝对值求幅频响应（Magnitude Response）并作π归一化
title('Magnitude Response');
axis ([0 2 0 12]);
xlabel('\omega/\pi');
subplot(2,1,2);
plot(w./pi,angle(X)); % angle(X)表示求其相频响应
title('Phase Response');
axis ([0 2 -4 4]);
xlabel('\omega/\pi');

给定系统Z域下的转换方程\(H(z)=\frac{∑b_kz^{-k}}{∑a_kz^{-k}}\)时，可以使用[H,w]=freqz(b,a,n)返回其频率响应H和对应的π归一化的角频率横轴w，其中a是\(∑a_kz^{-k}\)由高次幂到低次幂排列时的系数向量，其中b是\(∑b_kz^{-k}\)由高次幂到低次幂排列时的系数向量，n为计算时所指定的N点FFT的点数，缺省值为512。
如下的例程中给出了如何绘制\(H(z)=\frac{1-0.5z^{-1}}{1-2z^{-1}+z^{-2}}\)的频率响应图：

b=[1,-0.5];
a=[1,-2,1];
[H,w]=freqz(b,a); 
plot(w,abs(H));  %取绝对值求幅频响应（Magnitude Response）
title('Magnitude Response');
plot(w,angle(H)); % angle(X)表示求其相频响应
title('Phase Response');

### 卷积函数 线性卷积计算使用命令conv(x,y)得到。
周期卷积计算可以使用命令toeplitz(x,y)得到，其中x,y为两个周期序列的主值序列向量，两个向量长度相同。 当两向量长度不等时，使用0进行填充。

滤波器设计

MATLAB中，可以使用fir1()函数来进行加窗法的程序设计，其具体表达为：
fir1(order,omega_c,filtertype,windowtype,"noscale/scale")
其中order表示滤波器的阶数；omega_c是π归一化后的滤波器截止频率；filtertype表示设计的滤波器类型，缺省值为低通滤波器"low"；windowtype表示使用的窗函数，缺省值为海宁窗；"noscale/scale"表示是否需要归一化。
其中常见的窗函数有：
- boxcar(l)：矩形窗
- hann(l)：海宁窗
- kaiser(l,beta)：凯撒窗
l 表示的是滤波器的序列长度，注意与滤波器的阶数作区分。

fir1()函数会返回滤波器的冲激响应序列，返回的冲激序列使用[H_f,w]=freqz(h)返回其幅度-频率响应H_f和角频率轴w。
其幅度值-频率响应可以通过求其绝对值abs(H_f)得到，相频响应可以通过angle(H_f)得到。
下面的例程展示了如何用MATLAB绘制一个序列长度为7，截止频率为0.5π的理想低通滤波器：

h = fir1(6, 0.5, "low",boxcar(7),"noscale"); % generate the filter
[hf,w] = freqz(h); % 频率响应
figure(1);
plot(w/pi,abs(hf)); % 幅频响应
xlabel("\omega / \pi")
title("Magnitude response");
figure(2);
plot(w/pi,angle(hf)); % 相频响应
xlabel("\omega / \pi");
title("Phase response");

下面例程用于生成一个序列长度131，截止频率0.5π，β=4.966的凯撒窗低通滤波器，例程如下：

% 生成一个序列长度131，截止频率0.5π，β=4.966的凯撒窗滤波器
h = fir1(130, 0.5, "low",kaiser(131,4.966),"noscale"); 
[hf,w] = freqz(h); % 幅度-频率响应
figure(1);
plot(w/pi,abs(hf)); % 幅度值-频率响应
xlabel("\omega / \pi")
title("Magnitude response");
figure(2);
plot(w/pi,angle(hf)); % 相频响应
xlabel("\omega / \pi");
title("Phase response");