遗传编程(GP)导论
本文最后更新于 2025年4月25日 晚上
遗传编程导论
Gennetic Programming.,John R. Koza,Riccardo Poli,Search Methodologies—Introductory Tutorials in Optimization and Decision Support Techniques, 2005.
Visualization of Evolutionary Process in Genetic Programming.,Wongsiriprasert, Chatchawan & Chongstitvatana, Prabhas & Prasitjutrakul, Somchai, 1998.
the home page of Genetic Programming Inc.., Genetic Programming Inc.,http://www.genetic-programming.com/, 2007.
术语
遗传编程(Gennetic Progamming)是一种针对复杂目标问题,基于对需求高层级下的描述,使用计算机描述自动给出的最优解的算法。
具体而言,遗传编程通过应用类似于自然界基因遗传的规律,对一组程序(Programs)进行筛选和迭代,最终生成对目标问题解决效果最好的程序。
个体的描述和表达
与遗传算法不同的是,遗传编程中不再像遗传算法那样使用固定长度的字符串(Strings)和线性结构来描述一个个体。而是通过程序(Program)和树形结构(称为语法树,Syntax trees)来编码可能的系统解决方法。
遗传编程中,一个程序可以理解为是可以被符号化和流程化的一个类(item),它可以是一个特征,也可以是目标问题的一种解决问题的策略。
这样编码方式使得对个体的描述能够更加准确,同时进行遗传操作时对个体的变化也更大。
比如:
\[max(x*x,x+3*y)\] 可以被树形化为:
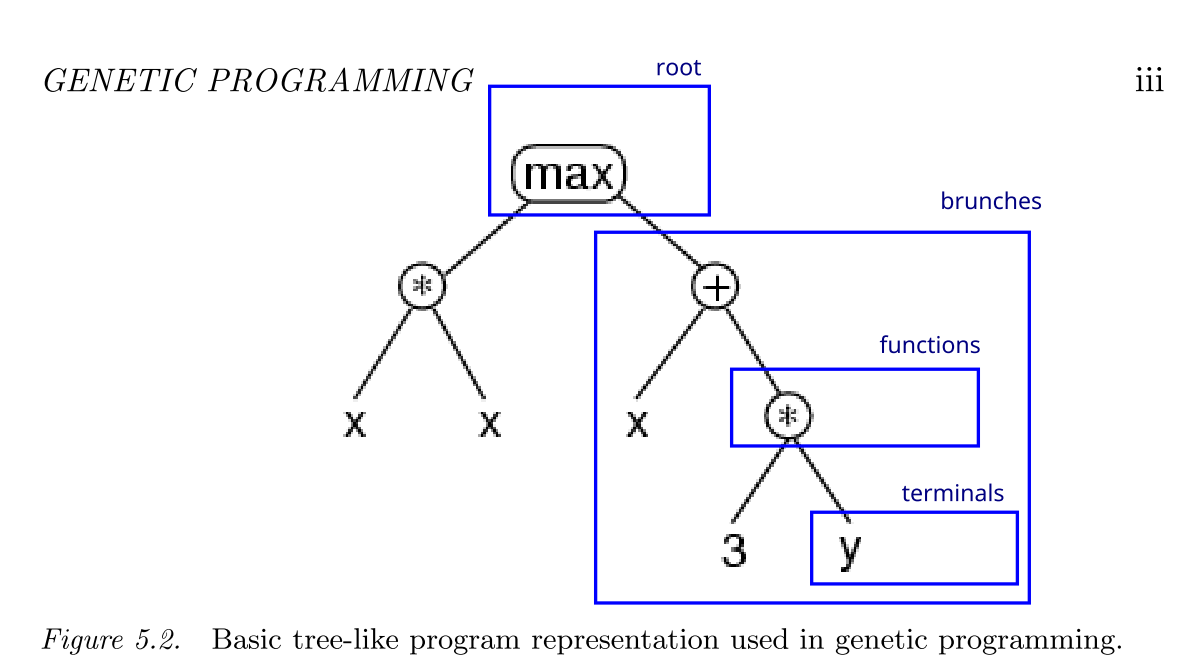
如上图所示,语法树由众多的节点(nodes)和节点之间的连接(links)组成,一个程序可以由语法树来描述其成分和执行流程,一个节点表示一个操作,在数学中可以理解为运算符,而连接可以表示某个节点与操作对象的对应关系,在数学中可以理解为运算数(Operand)。一个基本的语法树包括如下的成分:
- 根(root)
最顶层的节点,表示程序的最外部操作。
- 函数(function)
语法树中内部的节点。每一个函数对应的子树称作分支(brunch)。
- 端点(terminal)
语法树中非操作符的成分,比如不相关的变量,常数等等,是树的结束。
每一个语法树分支的类型和分支的数量称为语法树/程序的结构(architecture)。
在遗传编程中更习惯用前缀表示法(profix-notation expression)来表达一个数学运算,前缀表示法中所有的运算符都前置以强调运算符,这样的表示也更接近语法树结构。比如\(max(x*x,x+3*y)\)可以表示为:
\[max(*xx)(+*3y)\]
运行前的准备
在运行遗传编程之前,程序的设计者应当准备如下步骤:
- 对目标问题,要决定目标问题每一个分支的端点,端点可以是独立变量、无变量数学运算、或者是随机常数等等,这些都以一个集合的形式给出。
- 确定每一个分支的函数,同样也以一个函数集对其指定。
- 确定适应度函数,即如何评估个体的优劣。
- 确定运行时的参数和调试、诊断参数。
- 确定何时终止程序运行的标准。
搜索空间的确定
第一步和第二步为遗传编程的运行确定了搜索空间,遗传编程将在这个空间内对特定的目标种群进行搜索。对于不同类型的目标问题,端点和函数有所不同。有时甚至函数并不是数学运算符,也有可能是目标问题中其他的可以被符号化、结构化和流程化的表达。通常,函数是通过对目标进行分解而得到的。但无论如何设置函数,函数集必须满足完备性,即函数集中的函数可以包括目标问题中所有可能的操作。
例如,如果目标是让扫地机器人在有障碍的房间中能够顺利的清扫房间。那么执行的函数集中应当包括:转向、前进、清扫、停止等等。
如果目标问题是对模拟电路进行自动综合(Synthesis),那么函数集应该能够让遗传编程程序自动的从电路器件库中选择器件进行创建,函数集可以是含有电阻、电容、电感、运算放大器等等的器件库。
适应度函数
同样的,第三步中的适应度函数(fitness function)也与目标问题有关,适应度函数的主要功能是评估和量化种群中每个个体的优劣程度。在遗传算法领域,个体的“优劣”通常指个体对实现目标问题的贡献程度。适应度评估是遗传编程中将对目标问题高层级的需求转义进遗传编程程序中的最基本的机制。
运行控制
第四步和第五步都是用于控制遗传编程程序的运行,第四步中为遗传编程指定一些参数,比如:种群大小、允许的个体(即程序)的最大大小(端点和函数的最大个数)、以及个体发生遗传操作(复制、交叉、突变等)的概率等等。
第五步则指定了遗传编程何时终止,数学上表征为何时收敛。可以通过指定个体的适应度达到某个阈值,或者是最大的运行代数来确定遗传编程何时终止。这些参数的设定都在“怎样算成功解决目标问题”这个大的背景问题下设定。
遗传编程的运行
遗传编程的运行从随机初始化个体形成初始种群开始,个体通过适应度函数对其量化评估,得到个体的适应度后,基于适应度,有概率地挑选个体进行遗传操作,生成下一代种群。整个运行的流程图如下所示。
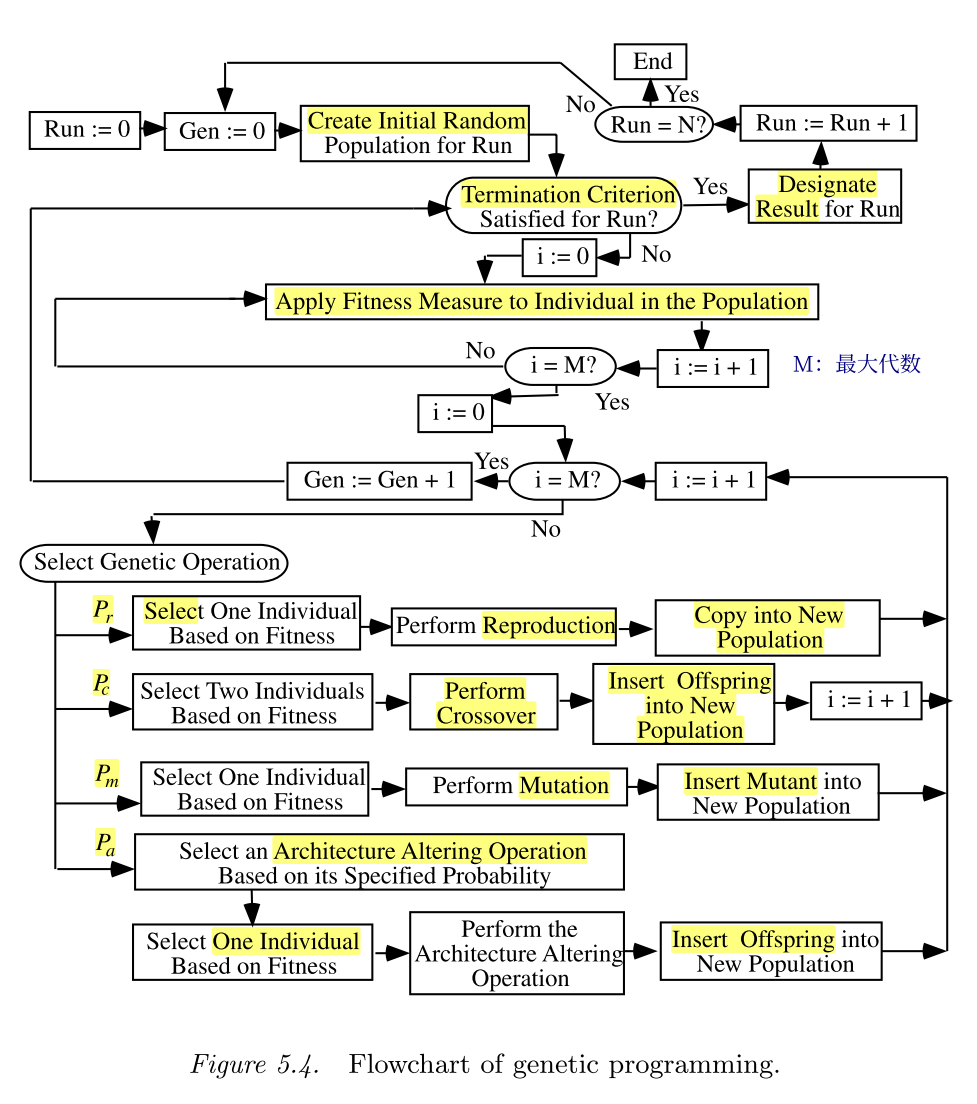
与遗传算法不同的是,遗传编程中的遗传操作是并行执行,而遗传算法中的遗传操作是串行执行的。并行执行可以使得原本优秀的亲代性状尽可能的被保存。(这一条意见被保留)
和遗传算法一样,遗传编程也是一种通用的解决问题的策略、不对某一个或是某一类问题进行特化(problem-independent)。
初始化个体
从函数集和节点集中随机挑选一些组成个体,并形成初始种群(第0代种群)。
初始种群中的个体通常是通过递归产生一个程序树,该树由随机选择的原始函数和终端组成。通常初始个体的大小设置为运行准备一节中所设置的最大大小。
初始化个体的常用方法有两种: “Full” 和 “Grow”。
Full Initialization
Full 初始化的方法的步骤是:
- 确定语法树的最大深度,即子树的最高层级。
- 从函数集中随机选择一些运算符,构建子树。
- 当达到最大深度时,从端点的集合中选择一些变量或者常数作为端点。
通过Full初始化方法,每一个个体只会在最深一层出现端点。
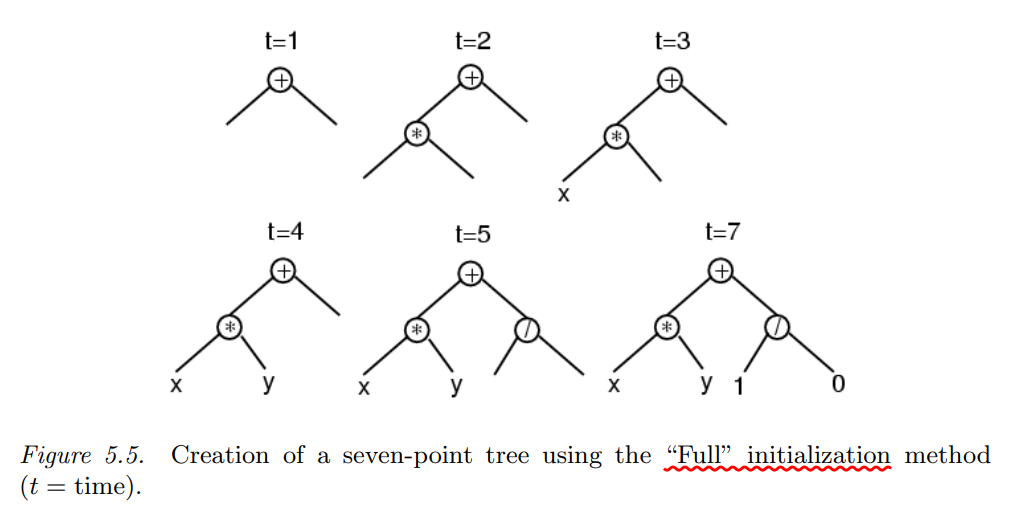
Grow Initialization
Grow初始化方法的步骤是:
- 确定语法树的最大深度,即子树的最高层级。
- 从函数集和端点集中同时随机选择一些运算符和运算数,构建子树,直到达到语法树的最大深度。
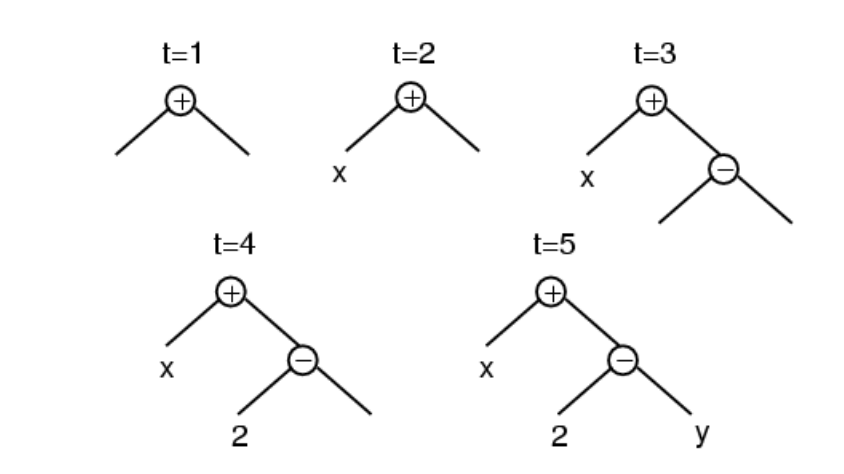
通过这样的随机生成方法,初始种群中会出现不同大小和形状的个体。 用grow策略生长得到的语法树往往不对称,而且普遍会比用户设置的最大深度浅一些;在变量的数量远大于函数的数量时,这种情况更明显。
下图动态展示了full和grow初始化:

这两种的随机初始化方法是对搜索空间的盲选。在python的遗传编程库gplearn中默认采用的是一半一半(half-half)的策略:一半的公式树用grow策略生成,另一半用full策略生成,以创造种群多样性。
> gplearn: https://gplearn.readthedocs.io/en/stable/
个体评估
个体的编译
当随机种群生成后,遗传编程进行迭代,并基于前一代个体筛选和变异生成下一代个体。每一次迭代的第一步是用适应度函数评估每一个个体,得到每个个体的适应度。评估过程需要多次运行当前种群中的每一个个体。常见的程序运行策略包括离线编译、在线编译、链接、虚拟机编译、解释等等。具体而言,需要将每个个体的树形结构转义为运算式后,在运算其结果,带入适应度函数中得到对应的个体适应度。
对树形结构的解释(interpretation)是一种一边编译一边运行的策略,解释遵循当且仅当这个函数下面的所有量都是已知的情况下,这个函数才会被运行。下图所示了一棵语法树在\(x=-1\)时的解释流程。
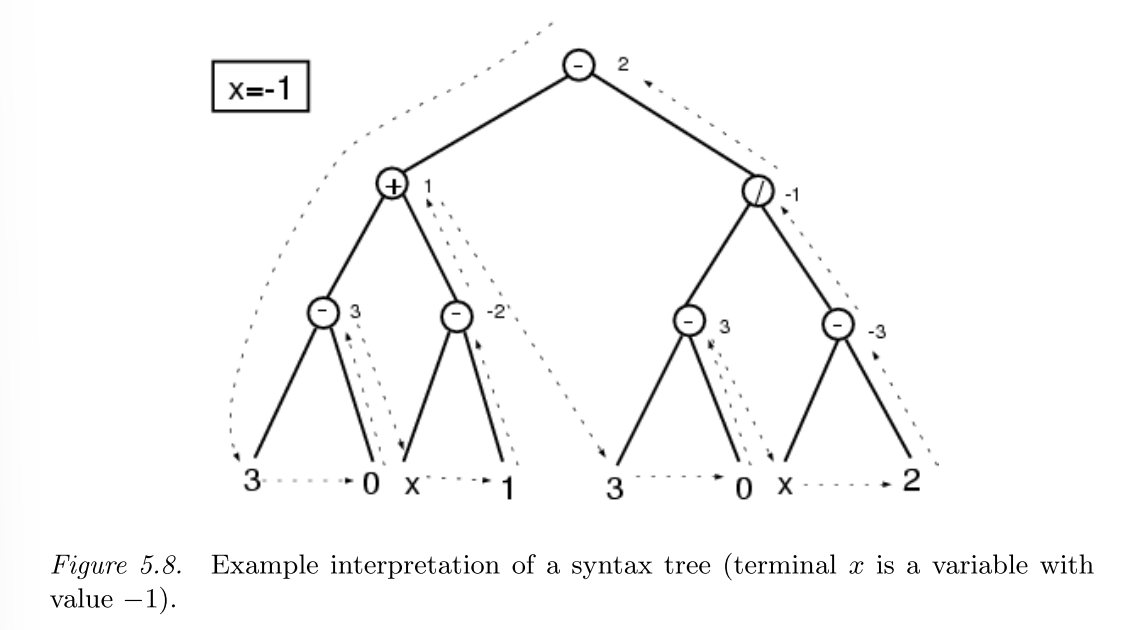
这种运行策略可以节省每一个个体的运行时间,加快评估速度。
适应度评估
对个体的适应度的评估依据于问题目标,比如个体的适应度可以是运行时间、运行中发生的错误数、计算资源消耗、或者是识别目标时的准确率等等。
个体也可以从多个维度去评价,并应用不同的适应度函数得到多个适应度结果。通常如果评测个体的指标有很多个,有必要对评测的指标进行降维操作。
许多问题中,每个个体的表现还与程序的输入、初始条件和运行环境有关,这些影响个体表现的因素称为适应度场合(fitness cases),每个个体在不同的场合下可能会有不同的适应度。
遗传操作
经过随机盲选得出的初始种群的个体适应度通常都不高,因此需要通过遗传操作(genetic operations)在搜索空间(searching space)内从这些初始个体周围开始寻找新的适应度更高的个体。
基于自然界的达尔文生物进化理论,遗传操作包括复制/繁殖(reproduction)、交叉(crossover)、突变(mutation),以及遗传算法中没有的结构变换(architecture-altering)。通过遗传操作产生的个体(称为后代)被移入下一代种群。
遗传编程基于个体的适应度,有概率的对个体进行这些遗传操作。通常个体的适应度越高,个体被选中进行遗传操作的概率就更高,这暗示了遗传编程将更倾向于在高适应度个体的周围去搜索搜索空间中的其他个体。通常选择个体进行遗传操作的算法有轮盘赌算法和锦标赛算法,这些算法都不是贪心算法,即是从全局而非当前的局部最优来考虑优化问题。这种非贪心的特性能够保证遗传编程/遗传算法不会陷入局部最优解。
贪心算法
在对问题求解时,总是做出在当前看来是最好的选择。即不从整体最优上加以考虑,贪心算法所做出的仅是在某种意义上的局部最优解。
交叉
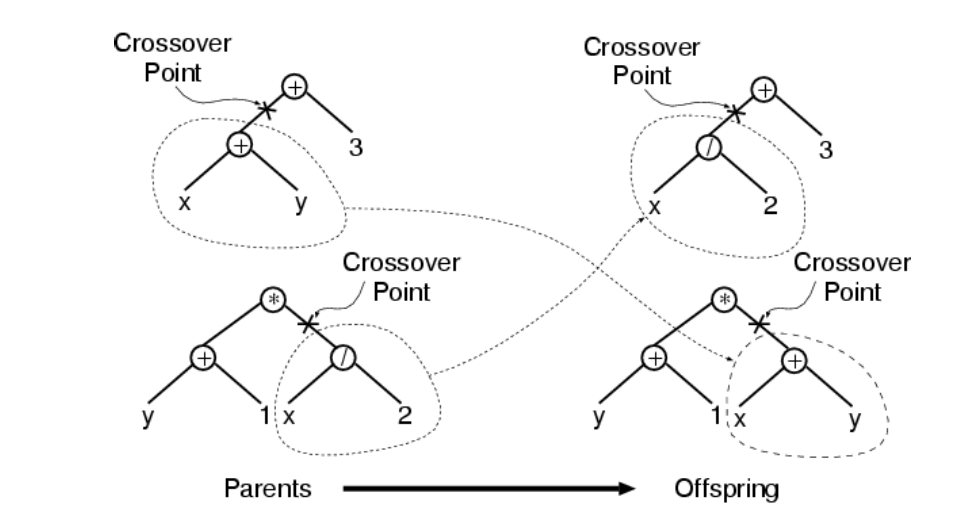
交叉的步骤是:
基于概率\(p_c\)和适应度从当前种群中选择两个个体,随机的选择两个个体某一位置上的一个连接或者结点作为交叉点,然后交换两个体交叉点以下的子树。
通常选择函数作为交叉点的概率要远高于端点作为交叉点的概率(比如90%的概率选择一个函数,10%的概率选择端点。),这是因为选择函数作为交叉点时,交叉对个体的影响更大,遗传编程在搜索空间中单次搜索的范围更广。
突变
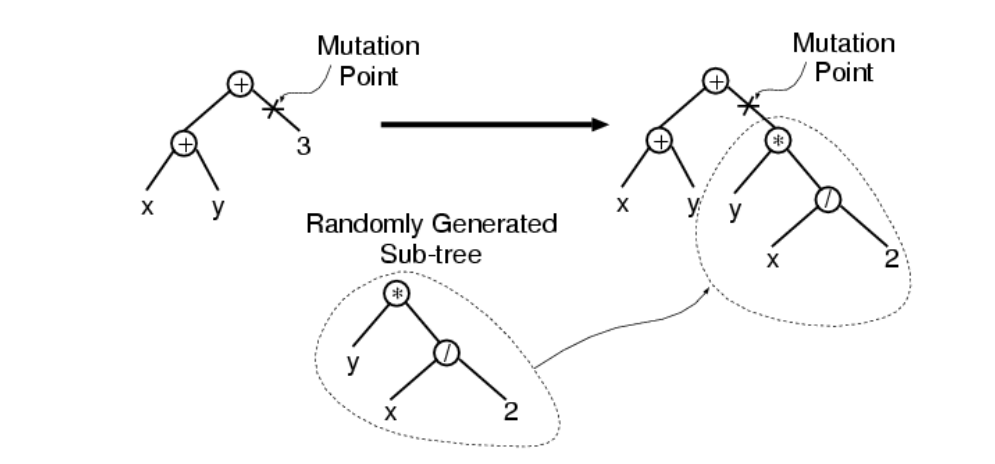
突变的步骤是:
基于概率\(p_m\)和适应度从当前种群中选择一个个体,并随机在这个个体内选择一个突变点,突变点下的子树被一个随机生成的子树替代(相当于与这个随机生成的子树发生交叉)。
复制
基于概率\(p_r\)和适应度从当前种群中选择一个个体,并复制到下一代种群中。
结构变换
结构变换会在之后的节中详述,在此不做叙述。
遗传操作执行结束后,后代组成的下一代种群会替代当前的种群,并再次进行“评估-选择-遗传操作”这样的迭代流程。直到遗传编程的运行达到一开始设定的终止条件。
由于初始种群中的每个程序是可运行的有效程序,遗传操作不会改变其有效性,因此后代也是有效的,可以说明通过遗传编程生成的最终程序是有效的。
遗传编程的运行案例
这一节将举例说明遗传编程是如何通过遗传操作解决目标问题的。目标问题为自动的生成一个程序使得其在\(x ∈ [-1,1]\)区间内生成的值满足函数\(x^2+x+1\)。这种试图发现某种隐藏的数学公式,以此利用特征变量预测目标变量的问题称之为符号回归(symbolic regression)类问题。
搜索空间确定和参数设置
对于这个问题,在遗传编程的准备阶段,端点集由随机常数和变量\(x\)构成:
\[T=\{X,ℜ\}\] 其中的\(ℜ\)表示一个随机数,人为地设置其范围为\(ℜ∈[-5.0,5.0]\)。
接下来指定遗传编程的函数集,可以将函数集设置为四则运算即可:
\[F=\{+,-,×,\%\}\]
为了避免运行错误,指定了\(ℜ÷0=1\)。
初始种群中的每一个个体都将从端点集和函数集中生成。生成之后的个体需要用适应度函数对其评估,在这个问题中,适应度函数可以通过当前个体\(\hat{y}\)与目标函数\(y_e=x^2+x+1\)在\(x ∈ [-1,1]\)上的值的差距来衡量。定义这个问题中的适应度函数为:
\[f(i)=∫_{-1}^1|\hat{y_i}-y_e|dx\] 对于这个适应度函数而言,个体的适应度越小代表与目标函数的差距越小,个体表现更加“优秀”。 接下来应当决定运行参数,为了简化解释,此处设定每一代中仅存在四个个体(但是实际上每一代的个体数量往往是成千或者百万级别的)并设置各遗传操作发生的概率,通常情况下设置交叉的概率为90%,繁殖的概率为8%,突变的概率为1%,结构变换的概率为1%。
GP通过交叉对搜索空间进行查找,因此交叉的概率应当比较大,才能保证搜索空间中的个体尽可能被搜索完全。
繁殖的概率比较低暗示了环境压力较大,选择比较严苛。
突变和结构变换的随机性会带来负面效应,因此应当尽量保持在非常低的水平
初始种群生成和个体评估
初始种群从搜索空间中随机挑选得到,这个例子中随机生成的初始种群中的四个个体如下图所示:
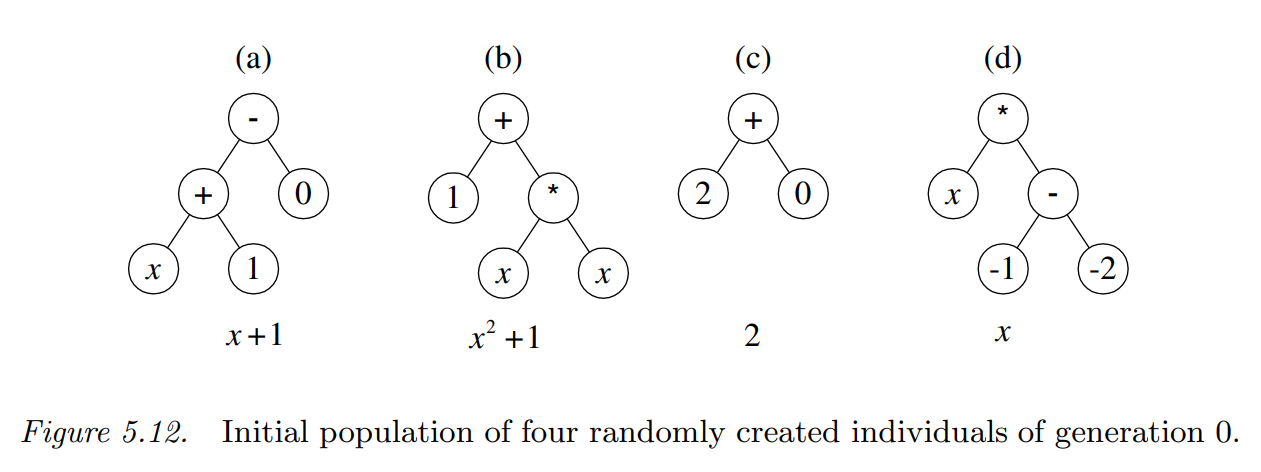
通过解释,这四个个体表示为:\(x+1\)、\(x^2+1\)、\(2\)和\(x\)。
将这四个个体\(\hat{y}\)分别带入适应度函数中,可以计算得出四个个体的适应度为0.67、1.0、1.67和2.67,可视化表示如下图所示:
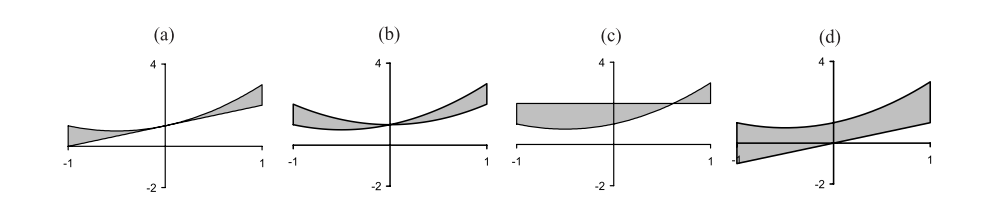
可以发现前两个个体(a)、(b)的适应度更低(或者说更“好”),在这个例子中意味着这两个个体更接近与目标,它们有更高的概率被选择做遗传操作。
遗传操作
复制
由于个体(a)适应度最好,它更有高概率被选择。此处假设它被选择出来进行复制操作,它被复制到下一代种群中。即它在下一代被保留。
突变
假设个体(c)的某个点位发生了突变,其下面的子树会被一个随机生成的子树替代,如图所示。
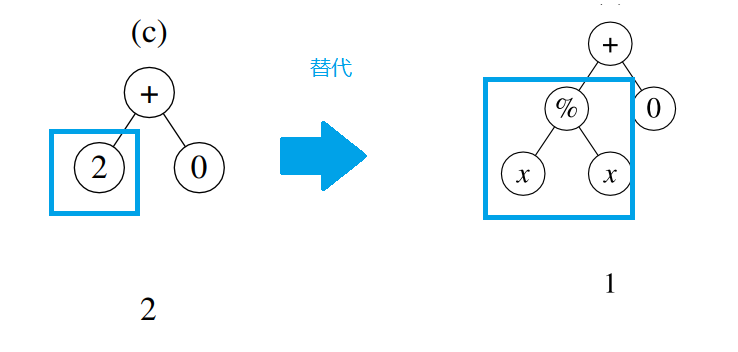
可以发现,原本适应度不佳的个体(c)通过突变后,其适应度可能会有所好转。除了在运行快要收敛时对现有种群施加扰动、改善算法的运行情况外,突变还能够有概率地改善适应度不加的个体的适应度,在搜索空间中调整在这些点附近的查找方向。
交叉
前两个个体(a)、(b)的适应度更好,更有高概率被选择配对进行交叉操作,假设(a)(b)个体发生如下图所示的交叉:
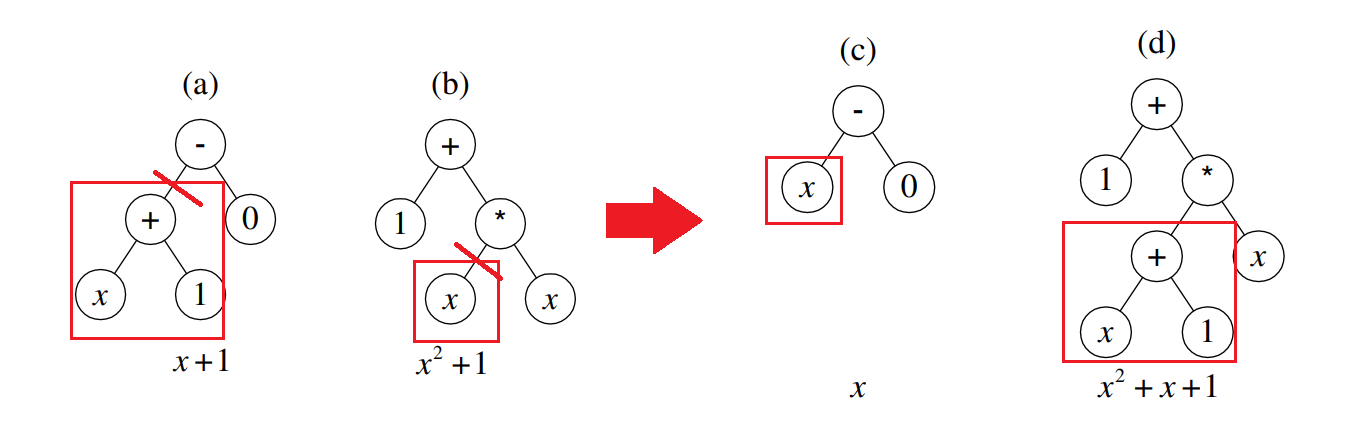
可以发现,个体(a)和个体(b)中各自都有一部分贴近于目标函数(称为各自的优良性状),通过交叉,两个亲本的优良性状更容易被结合,从而生成更加贴近目标的后代。
终止
通过遗传操作后的后代如下图所示:
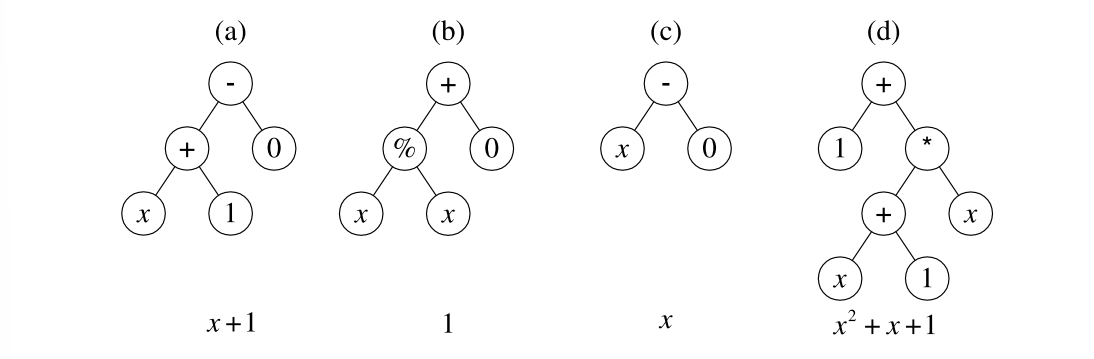
可以发现,个体(d)的适应度已经为0,达到了预先设定的终止条件,遗传编程停止运行。
遗传编程的高级特性
除了可以通过上述简单的例子表现出来的遗传编程的选择机制之外,遗传编程还拥有许多高级特性,在此进行简单介绍。
强类型
强类型(Strong type)指的是程序中表达的任何对象所从属的类型都必须能在编译时刻确定。
强类型是针对类型检查的严格程度而言的,它指任何变量在使用的时候必须要指定这个变量的类型,而且在程序的运行过程中这个变量只能存储这个类型的数据。因此,对于强类型语言,一个变量不经过强制转换,它永远是这个数据类型,不允许隐式的类型转换(例如Python中变量的数据类型取决于赋值而并非事先声明)。
上面的例子中,端点集和函数集并不是非常严格地指定了数据类型(比如上面的例子中端点集可以是常数,也可以是随机变量,函数也没有严格地指定输入的数据类型)。但是大部分问题对程序的要求都需要指定程序输入和输出的数据类型:比如在扫地机器人的例子中,函数“旋转”的输入一定是一个角度值,而“前进”的输入一定是一个距离。
将强类型语法应用于遗传编程中,用于限制树的结构和构成方式。在强类型的遗传编程随机过程中,如果一个下层节点的输出类型和它连接的一个上层节点输入类型不一致,那么存在这种连接的树会被丢弃。
在生成初始个体时,应该使所有的初始个体都满足强类型语法,并且要使得所有的遗传操作也要满足强类型语法的条件,这样最终筛选出来的个体也会是强类型的。
自动定义函数
像人类编程的程序中会编写子函数一样,遗传编程会利用问题对称性、规律性和模块性的特点,将个体之间结构、形状相似的部分自动定义为若干个小模块/子程序,称为自动定义函数(Automatically defined function,ADF),这些模块允许在重用时其输入的变量根据问题的不同而变化。
通常ADF的端点集和函数集与主程序的端点集和函数集有所不同。
自动定义函数会随着与主程序一起动态演化,并且可以在进化过程的同时被调用和递归调用。
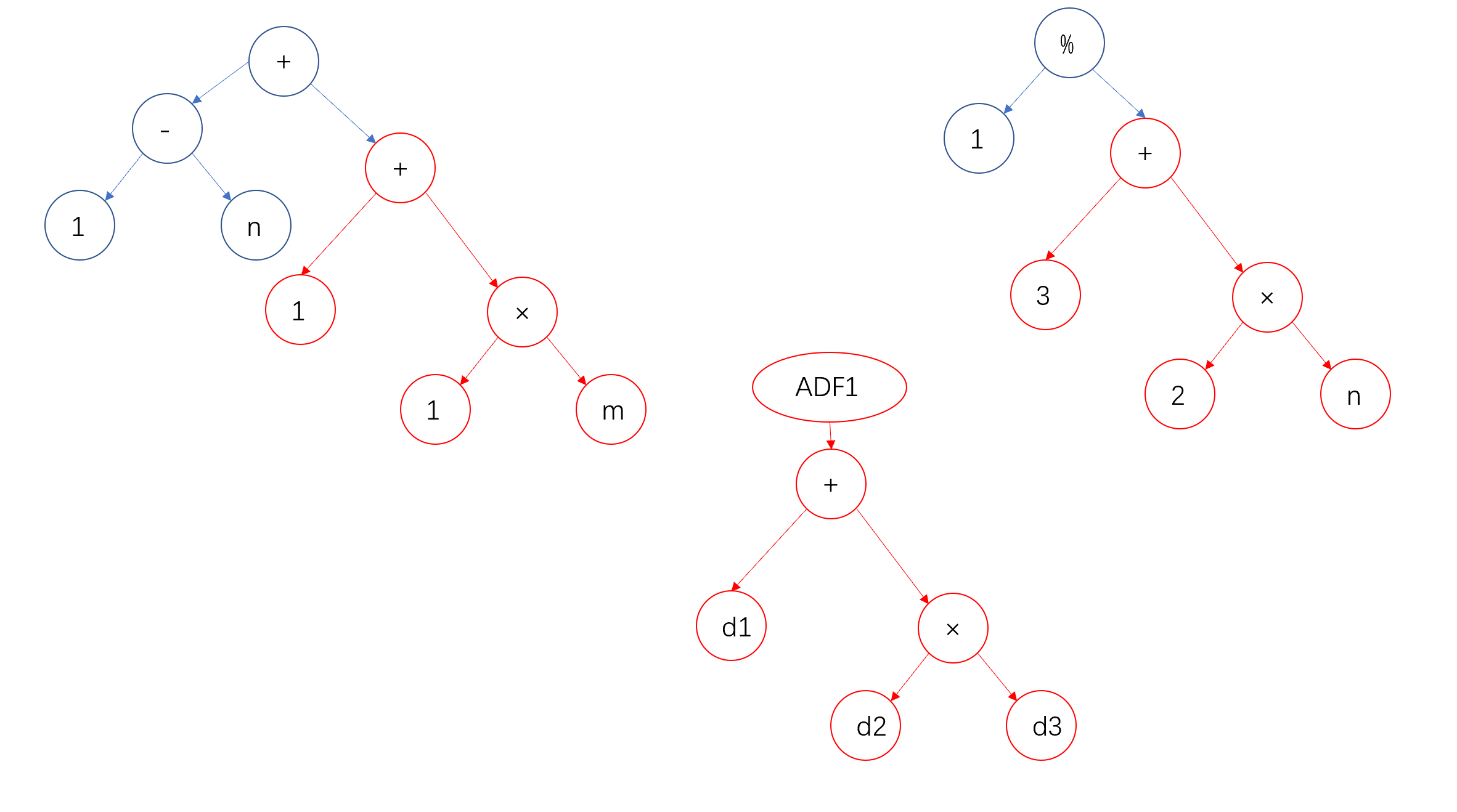
自动定义函数机制使得遗传编程能参数化重用和分层调用某一个模块,减小进化过程的回归压力,降低计算量。在问题层面上,自动定义函数机制能够将问题分解为若干个模块、简化问题的解决流程。随着问题的复杂程度上升,自动定义函数机制可以明显的减缓计算量和个体大小的上升,实验表明,在复杂问题中应用这样的机制简化计算是非常有效的。
程序的结构和结构变换操作
程序的结构
在遗传编程中,个体/程序的结构(architecture)包括:
- 分支的总数量
- 分支的类型(比如有自动定义函数分支,自动定义迭代分支,自动定义循环分支,解决生成分支)
- 每个分支中端点/声明的数量
- 分支的层级
结构变换
在遗传编程中,如何找到目标个体的结构也是一个问题。结构变换操作(architecture-altering operations)提供了一种方法:在遗传编程运行期间动态地向单个程序添加和删除子程序和其他类型的分支并添加或删除它们的参数。结构变换是针对一种程序结构的遗传操作,迭代运行结构变换后可以给出一个符合目标比较好的程序结构。由于结构变换本身具有破坏性,通常结构变换发生的概率很小,只有0.5%-1%。
有如下的几种常见的结构变换操作,如下表所示:
| 操作类型 | 说明 | 图示 |
|---|---|---|
| 子程序重复 subroutine duplication |
复制单个程序中预先存在的子程序,并为其副本指定新名称,并将预先存在的调用到该子程序的树复制为两部分。 此操作通过扩展整个程序中子程序的层次结构来改变整个个体的结构。与自然界中的基因复制一样,这种操作在第一次发生时保留了语义。这两个子例程通常在稍后发散,有时产生专门化。 |
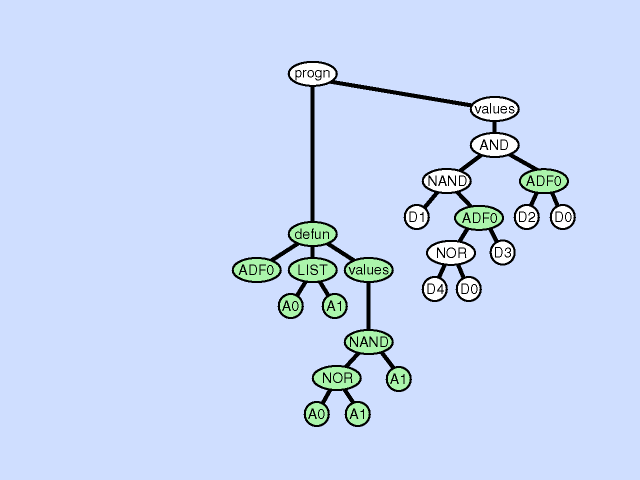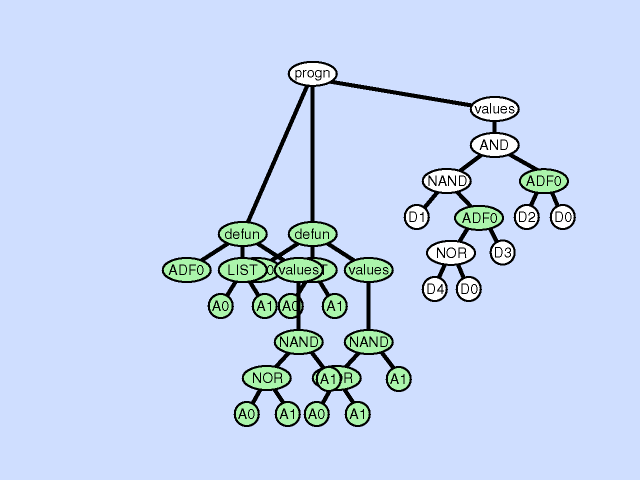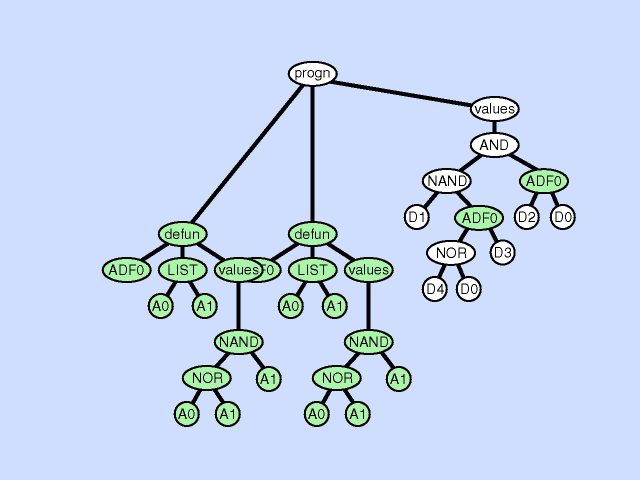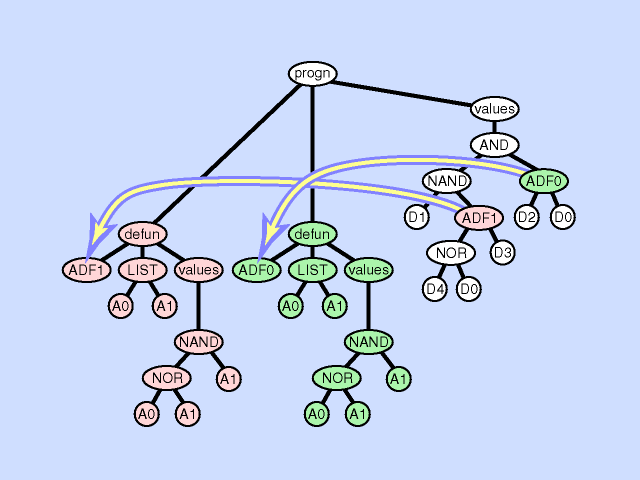 |
| 子程序缺失 subroutine deletion |
删除一个子程序分支 | 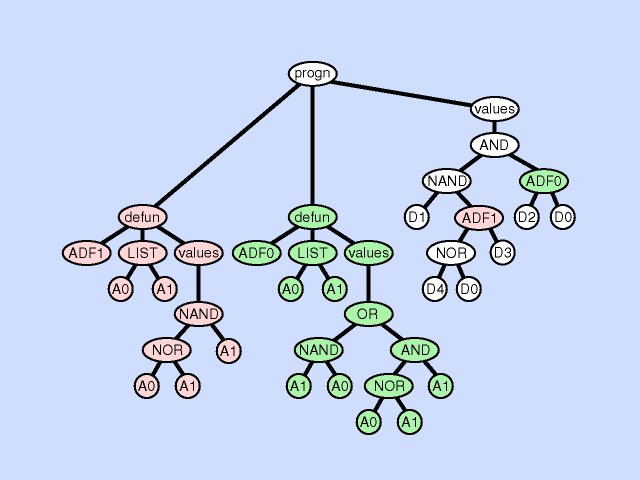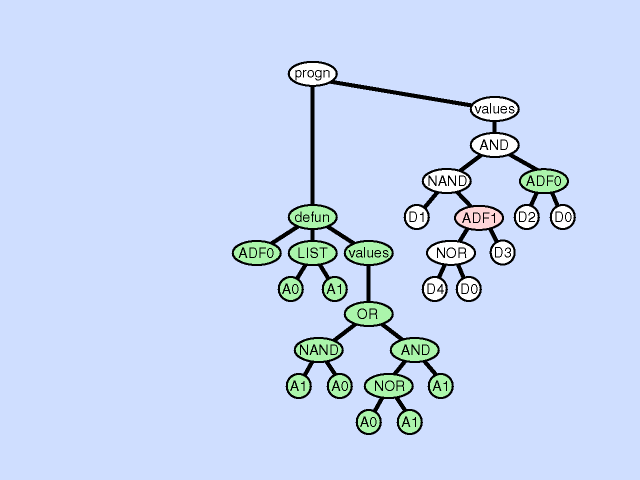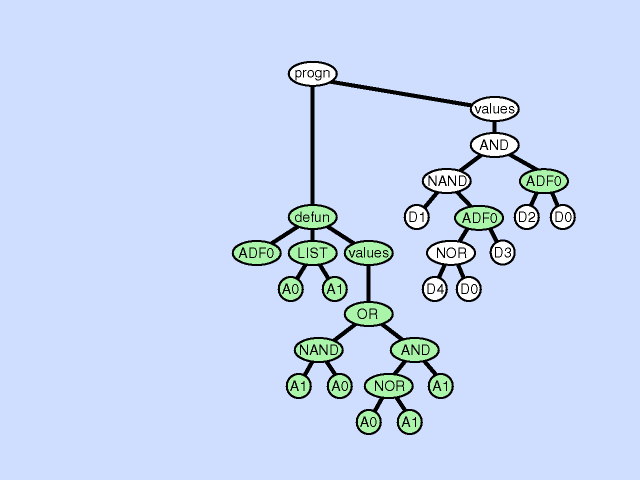 |
| 子程序创建 subroutine creation |
使用主结果生成分支的一部分创建新的子例程,从而通过在主程序和新的子程序之间创建分层引用深化整个程序中引用的分层。子程序创建操作还可以从现有子程序的一部分创建一个新的子程序,通过在先前存在的子例程和新的子程序之间创建一个层次引用以及一个更深更复杂的整体层次结构,进一步深化引用的层次结构。 | 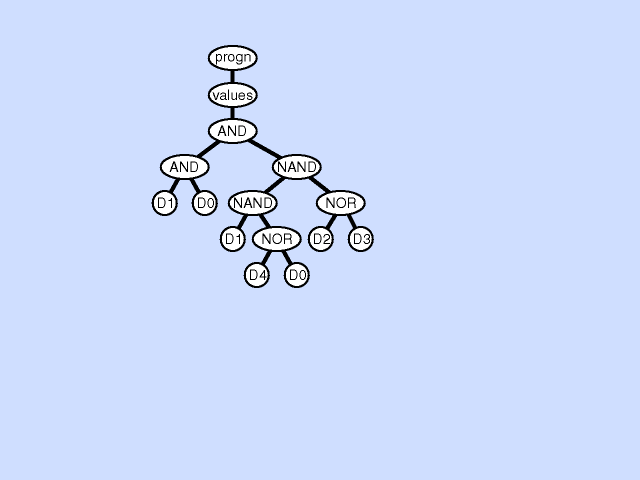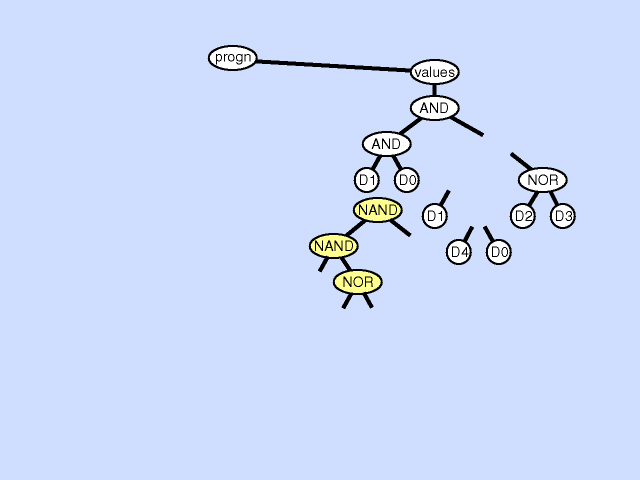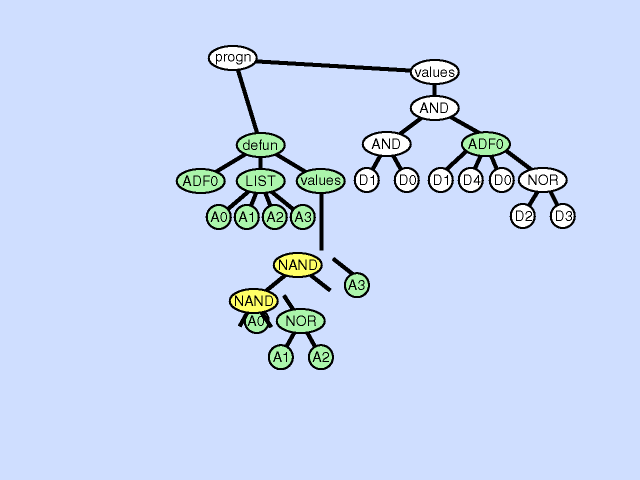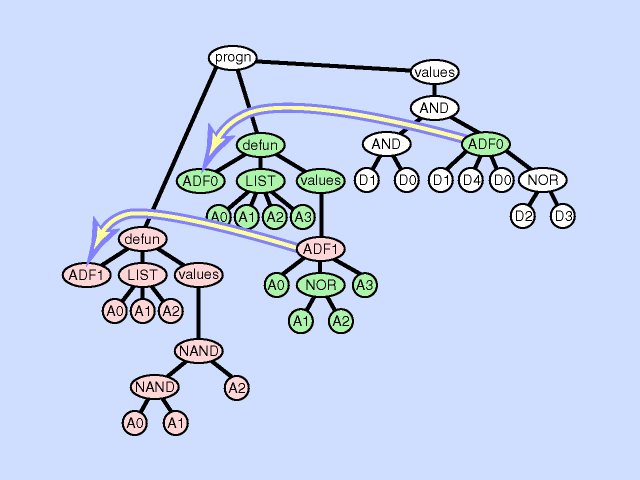 |
| 声明重复 argument duplication |
复制子程序的一个参数,随机划分对它的内部引用,并通过调整对子例程的所有调用来保留整个程序语义。此操作放大了子例程操作的子空间的维数 | 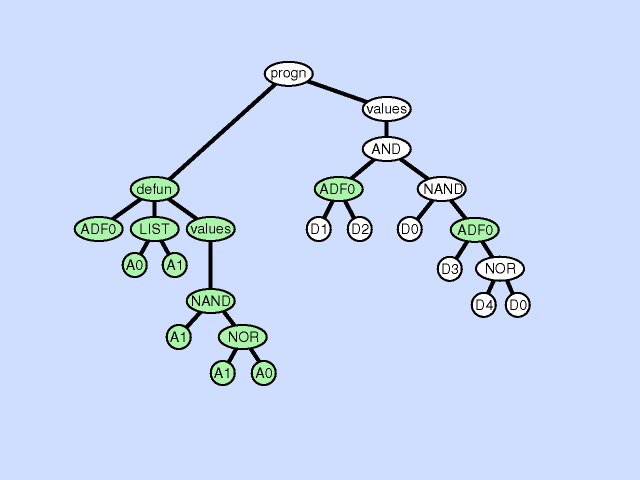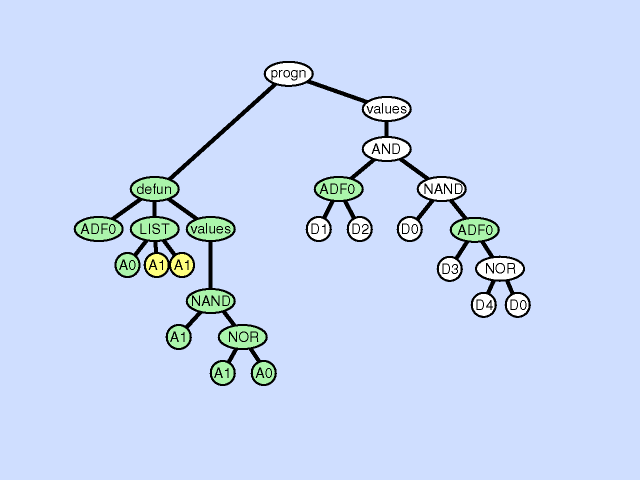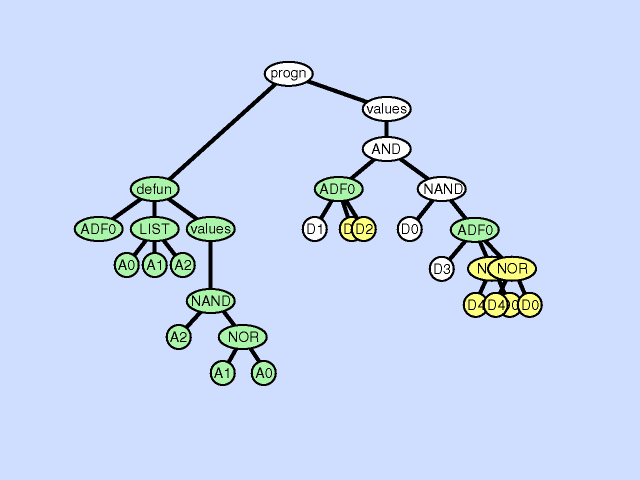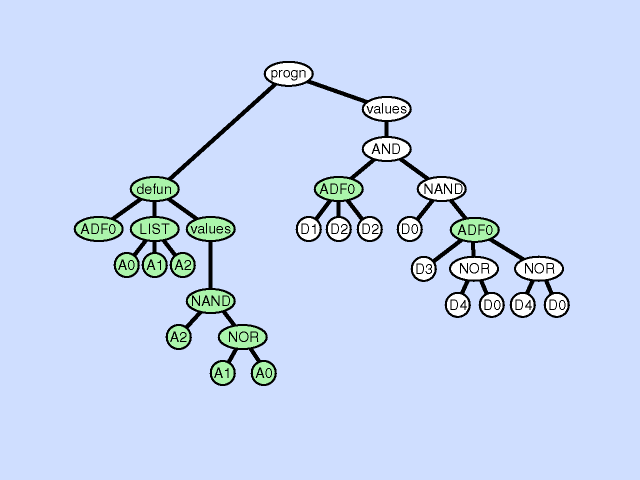 |
| 声明缺失 argument deletion |
删除某个子程序下的参数 | 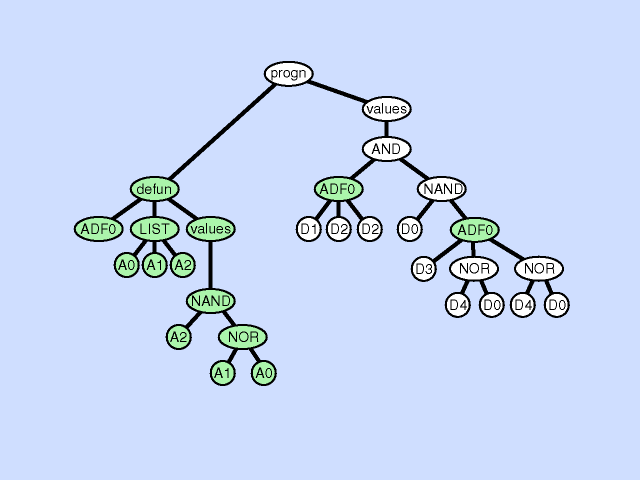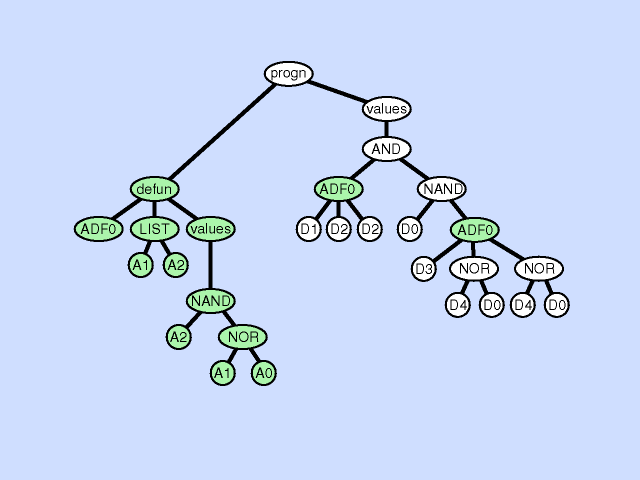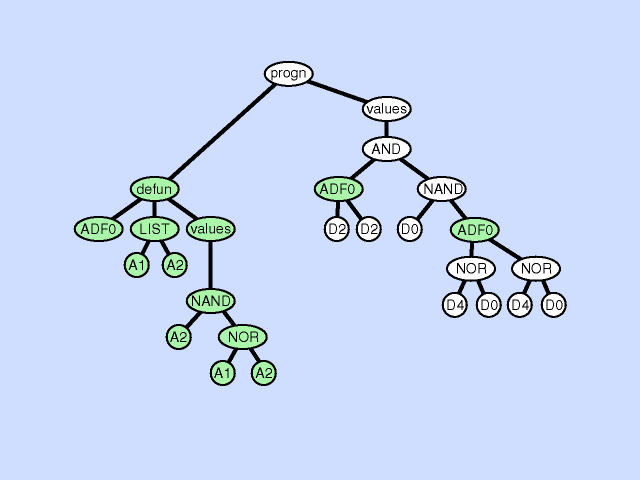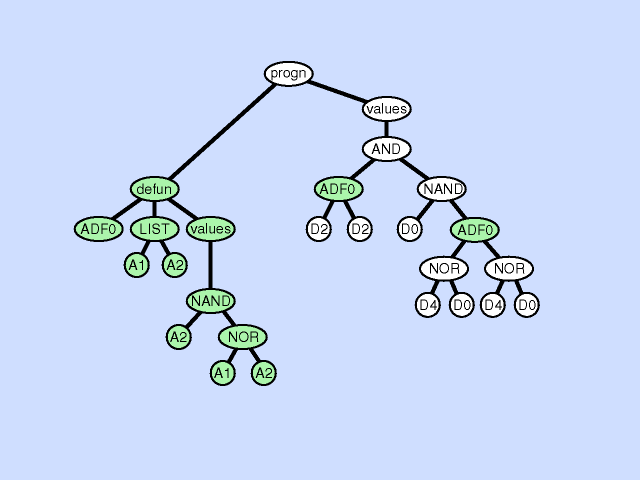 |
总而言之,结构变换提供了一种寻找目标个体结构的方法,其优点是能够随着主进化过程一同动态变换。
除了结构变换外,寻找目标个体结构的方式还有:
- 人为设置程序的结构
这种方法是一种静态设置的方法,适合在能够通过经验判断目标结构、目标结构比较简单时使用,可以节省计算量。
- 使用遗传编程进化出合适的目标结构
这种方法需要像上述运行流程一样首先随机生成若干个结构,应用迭代和筛选选择出合适的目标结构,相比于结构变换操作,这种方法的计算量较大,但是产生的目标结构可能更为贴切。
遗传编程的理论分析
遗传编程的的本质是一种在程序组成的搜索空间内搜索目标问题最优解的搜索方法。在最初阶段,遗传编程会从搜索空间中随机的几个点(即初始种群)开始搜索,这些个体中优于平均水平的个体会通过遗传操作在它们的周围搜索更优秀的个体,随着遗传编程的进行,这些随机分布的点会朝着某一方向移动,最终聚拢。
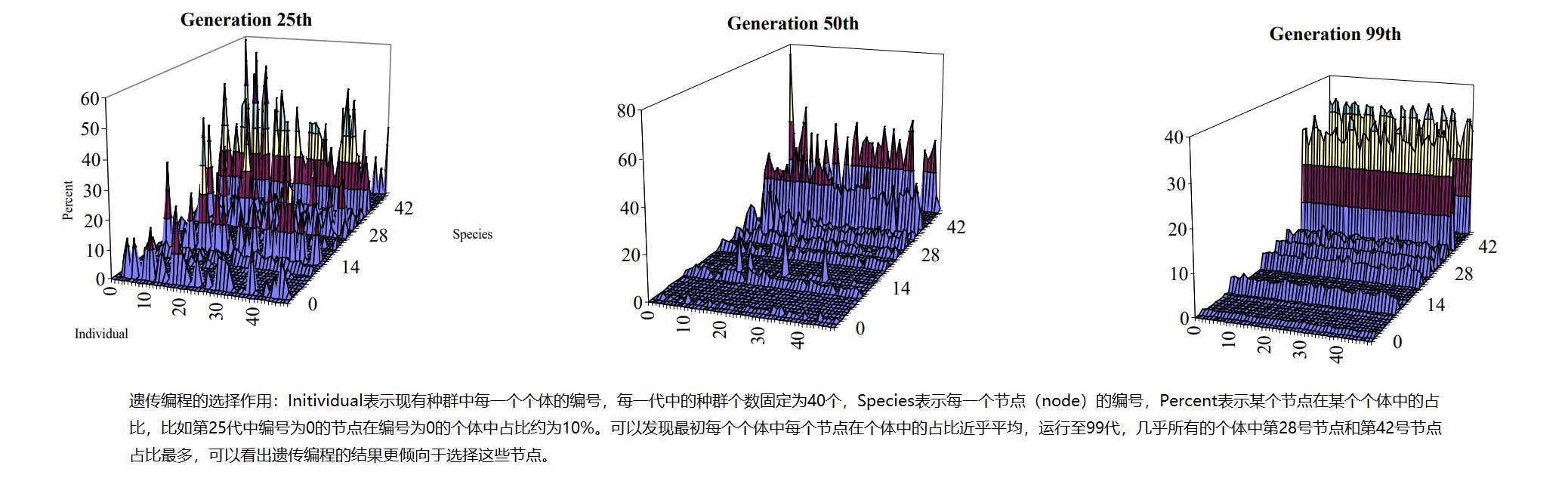
不过在高维和复杂的搜索空间中去可视化这样的过程从而探究遗传编程的运行机理不太可行,另外一种探究遗传编程的运行机理的方式是在相同条件下运行数次遗传算法,观察运行结果,通过经验和分析运行过程中的一些参数变化得出结论。这种方法很容易出错,因为遗传编程系统是一个复杂的自适应系统,有无数个自由度。因此,任何少量的统计描述符都可能只能捕捉到这样一个系统复杂性的一小部分。
由Holland提出的模式理论(schema theory)是另一种可行的解决方法,模式理论可以基于上一代种群的信息,推演出现有种群中某个特定个体的进化性质。
在遗传编程中,模式是一种含有通配符(don’t care)的树,通配符可以是一些函数或者端点。一个特定的模式可以代表所有的与这个模式形状结构相同、大小相同、非通配符节点也相同的一类个体,一个模式代表了一个子种群(sub-population)。
比如模式\(H=(\*x(+y\*))\)可以表示:\((+x(+yx))\),\((+x(+yy)),(\%x(+yx))\)等等个体。
令\(α(H,t)\)表示模式\(H\)在\(t\)代的进化采样率,即在\(t\)代中模式\(H\)中的个体得到进化的概率,即\(t+1\)代种群中有模式\(H\)中的个体数目与\(t+1\)代种群中的总个体数目之比,\(α(H,t)=p(H,t+1)\)。假设进化过程中只有复制和单点交叉发生,那么\(t\)代个体中含有\(H\)的概率分为两部分:\(H\)中的个体被复制到下一代的概率和现有种中交叉产生的后代在\(H\)中的概率:
\[α(H,t)=P_r[\text{via repoduction}]+P_r[\text{via crossover}]\] 设每个个体发生复制的概率为\(p_r\),发生交叉的概率为\(p_c\),\(p_c+p_r=1\):
\[α(H,t)=p_rP_r[\text{via repoduction}]+p_cP_r[\text{via crossover}]\] 对于前项,选择\(H\)中的个体发生复制的概率为:
\[P_r[\text{via repoduction}]=p(H,t)=P(H,t)\frac{f(H,t)}{\overline{f}}\] 其中\(P(H,t)\)表示从第\(t\)种选择一个来自\(H\)的个体的概率,\(\frac{f(H,t)}{\overline{f}}\)表示均值归一化后的\(H\)的平均适应度。
对于第二项,选择两个个体,它们的形状为\(k\),\(l\),已知形状\(k\)和\(l\)在交叉点\(i\)和\(j\)被选择时,发生交叉后的个体会落入模式\(H\),那么通过交叉产生个体落入\(H\)的概率分解为两步:
- 从所有配对的亲本中选择出形状\(k\)和形状\(l\),这个概率记为\(P_r[k,l]\)。
- 在形状\(k\)中选择出交叉点\(i\),在形状\(l\)中选择出交叉点\(j\),这个概率记为\(P_r[i,j|k,l]\)。
根据条件概率公式,有选择形状\(k\),\(l\)且选择出交叉点\(i\),\(j\)的概率为:
\[P_r[i,j,k,l]=P_r[i,j|k,l]×P_r[k,l]\] \[P_r[\text{via crossover}]=∑_{k,l}∑_{i,j}P_r[i,j,k,l]\] 假设形状相同的个体中的每个交叉点被选到的概率是相同的,在形状\(k\)中选择出交叉点\(i\),在形状\(l\)中选择出交叉点\(j\)均为其形状中含有的节点数分之一:
\[P_r[i,j|k,l]=\frac{1}{nodes_k}×\frac{1}{nodes_l}\] 对于\(P_r[k,l]\),为了简化计算,假设两个树中一个树的某个节点上方满足在\(H\)内的个体的结构,另一个树的下方满足在\(H\)内的个体的结构,那么:
\[P_r[k,l]=P_r[k]×P_r[l]\] \(P_r[k]\)和\(P_r[l]\)分别表示从\(t\)代中选择这两种形状的个体的概率: \(P_r[k]=p(k,t)\),\(P_r[l]=p(l,t)\)。
\[P_r[k,l]=p(k,t)×p(l,t)\]
进而可以给出理论上\(H\)的采样率下界:
\[α(H,t)=p(H,t)+∑_{k,l}∑_{i,j}\left[\frac{1}{nodes_k}×\frac{1}{nodes_l}×p(k,t)×p(l,t)\right]\] 通过采样率下界,可以估计子种群\(H\)经过遗传操作,下一代中个体在子种群\(H\)中的数目的期望为:
\[E[M(H,t+1)]=M(H,t)α(H,t)\] 由于\(p()=P()\frac{f()}{\overline{f}}\),可以发现整个采样率\(α\)的表达式与子种群\(H,k,l\)的采样率及其适应度有关:子种群\(H,k,l\)的适应度\(\frac{f(H,t)}{\overline{f}}\),\(\frac{f(k,t)}{\overline{f}}\),\(\frac{f(l,t)}{\overline{f}}\)的适应度越高,\(H\)的采样率\(α\)就越高,进而可以推出:随着遗传编程的运行,每一代种群中适应度高的子种群越倾向于被保留,采样率逐步升高。 理论上,在经过若干次进化后,种群中的所有个体都将是搜索空间中适应度较高的个体。