03.模糊系统

模糊系统

模糊逻辑

生活中人们在描述对某些系统的设置时常常并不是使用准确的数值来表述这些设置，而是使用较为模糊的语言来描述：例如人们通常会说“将空调温度调高一点”而非“将空调温度调高1摄氏度”。在系统工程中，专家通常依赖于基于经验的直觉来解决问题，这些直觉通常也是模糊的(vague)。
那么如何让计算机理解这些模糊的设置呢？模糊逻辑(fuzzy logic)就是一种使用逻辑来描述设置中的不确定性和模糊性的方法论。模糊逻辑基于模糊集论(fuzzy set theory)，它试图使用近似和不确定的信息来模仿人类的直觉推理。模糊集论使用数学表达来描述这样的不确定和模糊。

有时也认为模糊逻辑和模糊集论是相同的概念。

基本定义

隶属度

对于传统的布尔逻辑，对某件个事件的描述分类是非黑即白的，即是二值的。而在模糊逻辑中，对于某个事件的描述分类是基于概率分布的，称为隶属度(DoM,Degree of Membership)，这是一种多值逻辑。
比如使用模糊逻辑描述一个人的身高：“小刘有15%的概率被认为是高的。”（这样的描述称为语义命题）其中的15%是“小刘身高”隶属于“高”这一分类的隶属度。

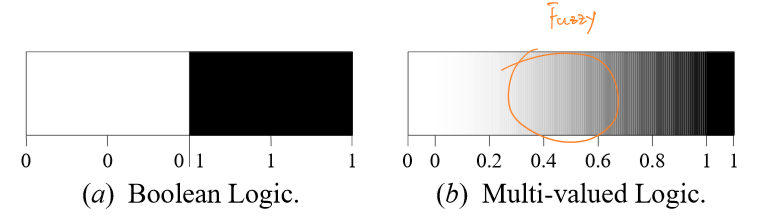
模糊集和隶属度函数

模糊集(fuzzy set)表示隶属于某个类别的所有个体。模糊集中所有个体各自的某一属性的所有可能取值(称为论域，univsersal of discourse)以及这个属性值对应该属性的隶属度可以被可视化为一条曲线，其值域范围为\([0,1]\)。

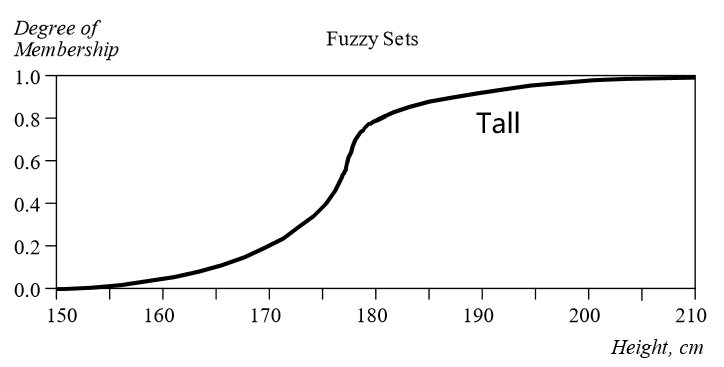
例如上图描述了被认为是“高”的模糊集以及各个体的身高对应的隶属度。比如图上的一点：\((180,0.78)\)的含义是：“身高为180cm的个体属于高的概率为78%”。

从上面的描述可以看出，模糊逻辑的实质是通过一个映射将具体的数值映射为概率表示的隶属度，从而实现对数值的模糊化。 在模糊集论中，这个映射被称为隶属度函数(membership function)\(μ_A(x)\)，表示了属性数值\(x\)，称为模糊变量(fuzzy variable)与隶属某一类概率的映射关系。这样的隶属关系表示为：
\[μ_A(x)=1,x\text{ totally in }A\] \[0<μ_A(x)<1,x\text{ partially in }A\] \[μ_A(x)=0,x\text{ not in }A\]

模糊集可以由隶属度函数和模糊变量定义，用扎德表示法(Zadeh presentation)写成：
\[A=\frac{μ_A(x_i)}{x_i}+...+\frac{μ_A(x_n)}{x_n}\] 其中一个\(\frac{μ_A(x_i)}{x_i}\)称为一个单例类（singleton），它不是一个分数，表示模糊变量\(x\)的个体\(x_i\)的隶属度为\(μ_A(x_i)\)。

隶属度函数的确定通常由专家根据实际经验得出。在许多情况下,经常是初步确定粗略的隶属函数，然后再通过“学习”和实践检验逐步修改和完善，而实际效果正是检验和调整隶属函数的依据。常见的隶属度函数是sigmoid函数和线性分段函数。
下面展示了有关于模糊变量：室内温度，评价为“冷”、“温和”、“热”的三个隶属度函数的表示：

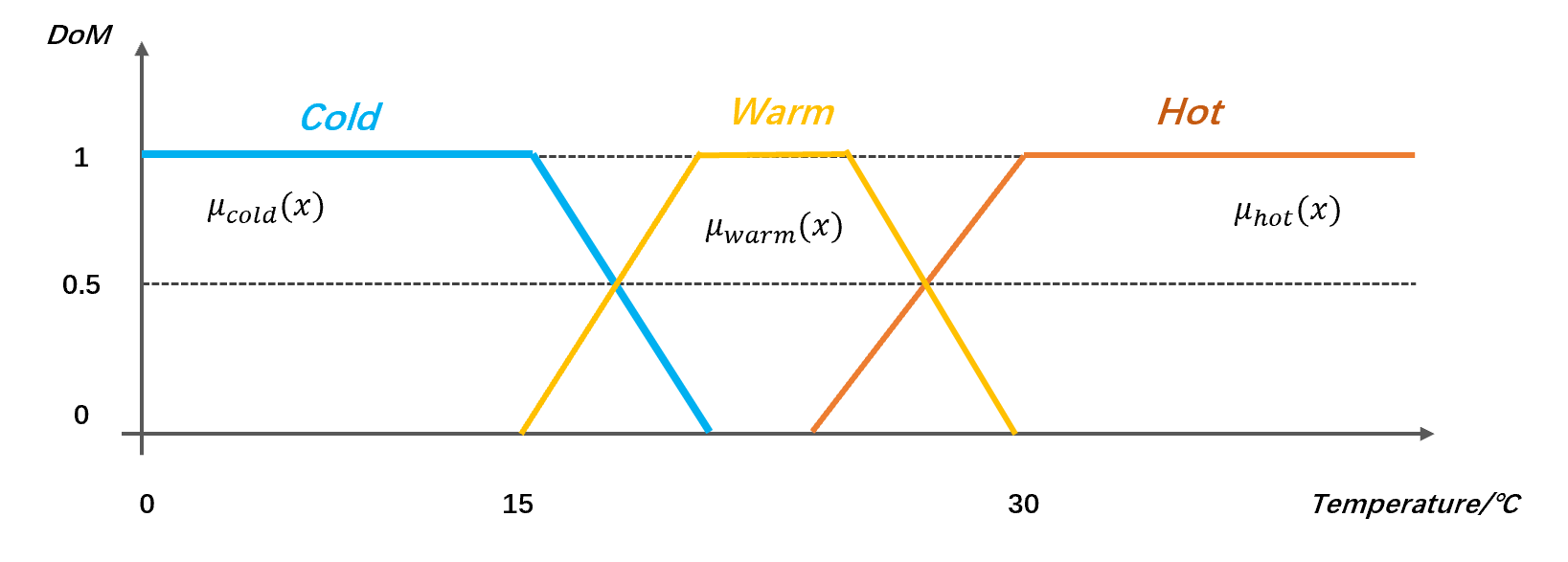
模糊限制语

在自然语言中，人们对于模糊变量的描述通常还存在某些修饰词，来描述属性的剧烈程度，比如：“很(very)”，“有一点(a littly)”，“真的(indeed)”等等。模糊逻辑中使用模糊限制语(hedges)来表示这些修饰。简单来说，如果属性前具有模糊限制语，那么属性对应的隶属度函数形状将会根据某些规则改变。下表展示了常用的模糊限制语对隶属度函数的影响：

模糊限制语	数学表达	图示 (细线为原隶属度函数)
非常 very	\([μ_A(x)]^2\)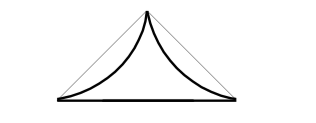
十分很 very very	\([μ_A(x)]^4\)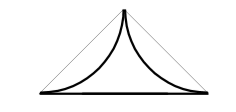
或多或少 more or less	\(\sqrt{μ_A(x)}\)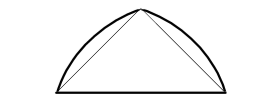
真的 indeed	\(2[μ_A(x)]^2,0≤μ_A(x)≤0.5\) \(1-2[μ_A(x)]^2,0.5<μ_A(x)<1\)

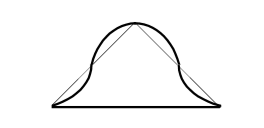模糊规则

模糊规则(fuzzy rules)用于描述若干个模糊变量之间的关系，用逻辑运算符（或且非等）和“IF...THEN...”结构表达。其中，"IF..."称为模糊规则的前项(antecendents)。
表示为：
IF \(x\) IS \(A\)
THEN \(y\) IS \(B\)
其中\(x,y\)是两个模糊变量，\(A\)和\(B\)是两个属性/模糊集。
例如：
IF wind IS strong AND temperature IS warm
THEN sailing IS good

模糊集操作

模糊集有关定义

• 空集
  当且仅当一个模糊集\(A\)内的模糊变量个体的隶属度都为0，称模糊集\(A\)为空集：
  \[A=∅⇔μ_A(x)=0\]

• α截集
  模糊集\(A\)的α截集(α-cut)为其集合中隶属度大于等于\(α\)的个体的全集：
  \[A_α=\{μ_A(x)≥α\}\]

• 正规性和高度
  当模糊集\(A\)的个体中中至少有一个的隶属度为1，称模糊集\(A\)是正规的(normality)。
  模糊集中个体隶属度的最大值表示该模糊集的高度。

• 支点
  模糊集\(A\)中隶属度大于0的所有个体组成的全集为模糊集\(A\)的支点(support)：
  \[supp(A)=\{μ_A>0\}\]

• 核
  模糊集\(A\)中隶属度等于1的所有个体组成的全集为模糊集\(A\)的核(core)：
  \[core(A)=\{μ_A=1\}\]

• 基数
  模糊集\(A\)的基数(cardinality)是其所有隶属度的和：
  \[card(A)=∑_xμ_A(x)\]

模糊集关系

模糊集关系表示两个模糊集之间的关系，有四种：交集(intersection)、并集(union)、补集(complement)和包含(containment)。

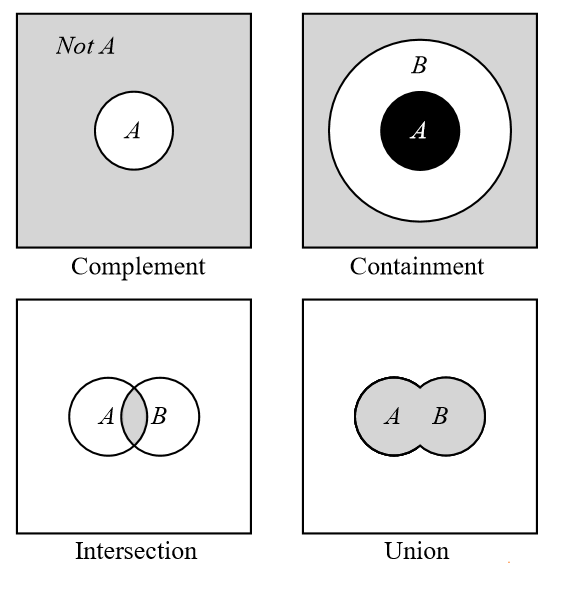
• 补集
  补集关系表示个体不属于模糊集\(A\)的概率。
  补集关系表示为1减去该模糊集的隶属度函数：
  \[μ_{\overline{A}}=1-μ_A(x)\]

• 交集
  交集关系表示个体属于两个模糊集交集\(A∩B\)的概率。
  交集关系表示为具有相同模糊变量的两个模糊集的每个隶属度取最小值：
  \[μ_{A∩B}(x)=min[μ_A(x),μ_B(x)]=μ_A(x)∩μ_B(x)\]

• 并集
  并集关系表示个体属于两个模糊集并集\(A∪B\)的概率。
  并集关系表示为具有相同模糊变量的两个模糊集的每个隶属度取最大值：
  \[μ_{A∪B}(x)=max[μ_A(x),μ_B(x)]=μ_A(x)∪μ_B(x)\]

• 包含
  如果一个模糊集\(A\)内的所有隶属度和模糊变量个体都属于模糊集\(B\)，称模糊集\(B\)包含模糊集\(A\).
  \[A⊆B⇔μ_A(x)≤μ_B(x)\]

• 全等
  如果一个模糊集\(A\)内的所有隶属度和模糊变量个体都与模糊集\(B\)相同，称模糊集\(B\)与模糊集\(A\)全等.
  \[A=B⇔μ_A(x)=μ_B(x)\]

模糊推理

知道模糊规则中蕴涵的模糊关系后，就可以根据模糊关系和输入情况，来确定输出情况，这就叫做模糊推理（fuzzy inference）。

Mamdani模糊推理

模糊推理技术中最常用的方法是Mamdani方法。1975年，伦敦大学的Ebrahim Mamdani教授建立了第一个模糊系统来控制蒸汽机和锅炉.他应用了一套有经验的人类操作员提供的模糊规则。
Mandani模糊推理的过程有4步：
- 对输入变量进行模糊化
在取得精确输入\(x\)和输出\(y\)(project funding and project staffing)的前提下决定这些精确(crisp)数据属于每个适合模糊集的程度。
例如将某个精确的输入\(x_1\)和其精确输出\(y_1\)应用到如下的规则中：

得到：

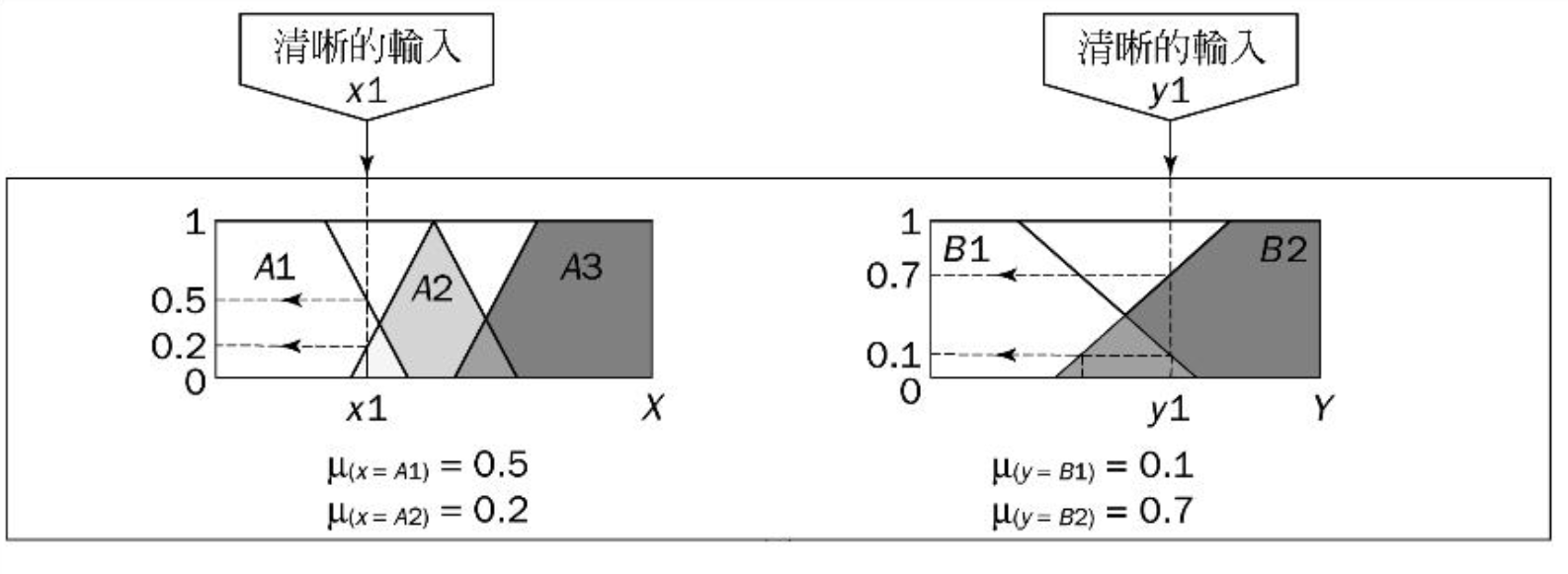
• 评估规则
  取得上一步中的模糊输入（比如例子中的：\(μ_{A_1}(x)=0.5，μ_{A_2}(x)=0.2,μ_{B_1}(x)=0.1,μ_{B_2}(x)=0.7\)），并将它们应用到模糊规则的前项(antecendents，即模糊规则中的IF表述)。如果已知的模糊规则存在多个前项，则使用逻辑关系符(AND或者OR)得到最终的一个输出值。并将得到的输出值使用α截剪切(clipping)后项对应的规则中。
  

  除了剪切外，有时也会使用缩放(scaling)。缩放提供了保持模糊集原始形状的更好的方法。这种方法损失的信息较少，在模糊专业系统中非常有用。
  

  
  

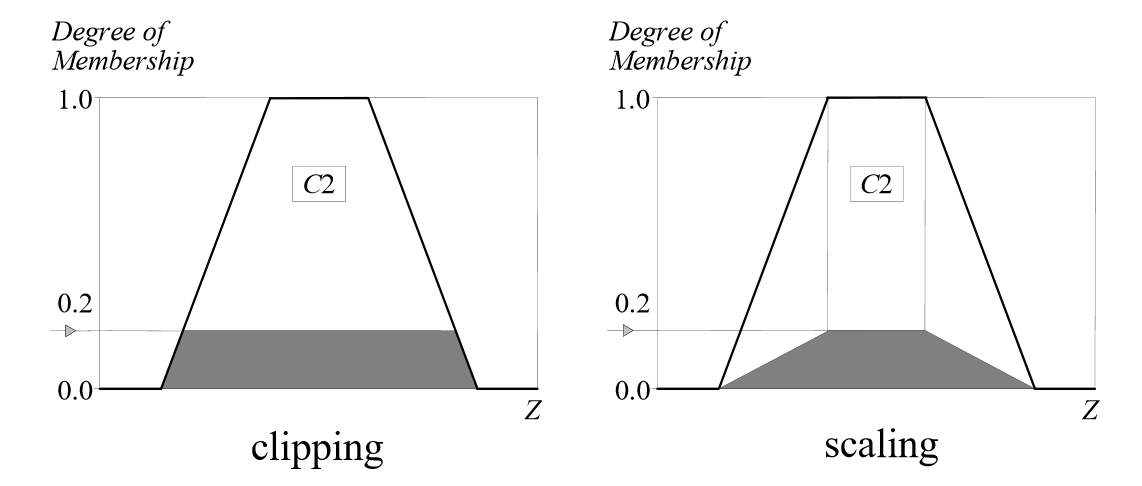
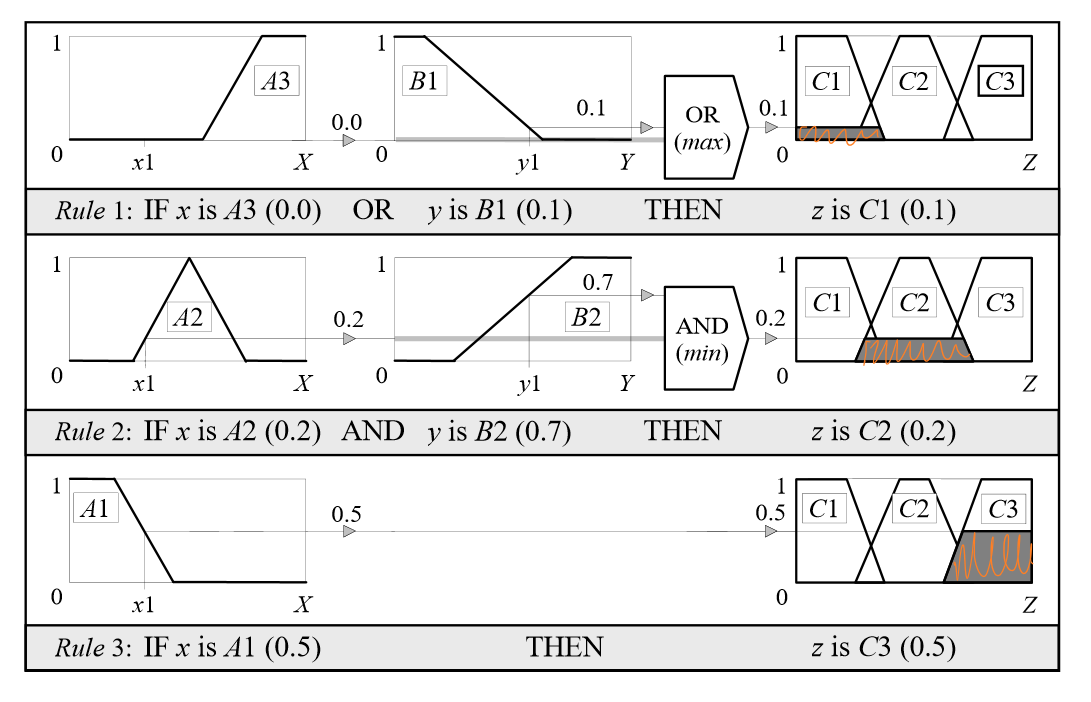
• 聚合规则
  将剪切好的多个后项规则合并到一起，拼合后的规则称为聚合集。
  

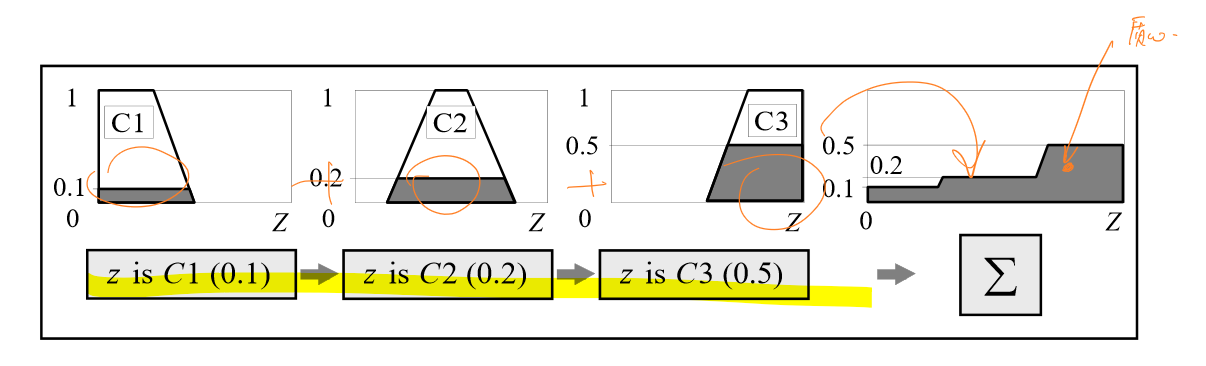
• 逆模糊化
  模糊系统最终的输出是一个数值，因此有必要将拼合好的规则通过某种方式聚合为一个数值。常见的方法有三种：

  • 质心
    质心表示了已知精确值对应模糊集的期望，这是最常用的逆模糊化方法。其垂线刚好可以将拼合好的规则面积分为两部分，质心的计算公式如下：
    \[COG=\frac{∑xμ_A(x)dx}{∑μ_A(x)}\]
  • Max-in和Min-in
    这两种方式表示了精确值对应模糊集的上下限，当聚合集具有多个最大值和最小值点时，有：
    \[Max-in=\frac{∑Max_iμ_A(x)dx}{∑μ_A(x)}\] \[Min-in=\frac{∑Min_iμ_A(x)dx}{∑μ_A(x)}\]

Sugeno模糊推理

Mamdani模糊推理需要通过整合连续变化的函数来逆模糊化，计算效率通常不高。而Sugeno在聚合规则时只会聚合每个规则下对应的一个单例类。整合时每个规则在该单例类下有值，其他区域的值均为0。因此Sugeno方法聚合规则并不需要聚合一个区域，只用聚合几个值即可，计算量大幅度减小。因此Sugeno模糊推理常常用于模糊神经网络（下文会详细介绍）的反向传播中。
最常用的是零阶-Sugeno模糊推理模型，它的规则表示为：
IF \(x\) IS \(A\) AND \(y\) IS \(B\)
THEN \(z\) IS \(k\)
其中\(k\)是一个常数。
在这样的规则表示下，每一个模糊规则的输出都是一个常数。所有规则的输出通过单例类表示。
Sugeno模糊推理的第二步评估规则表示如下:

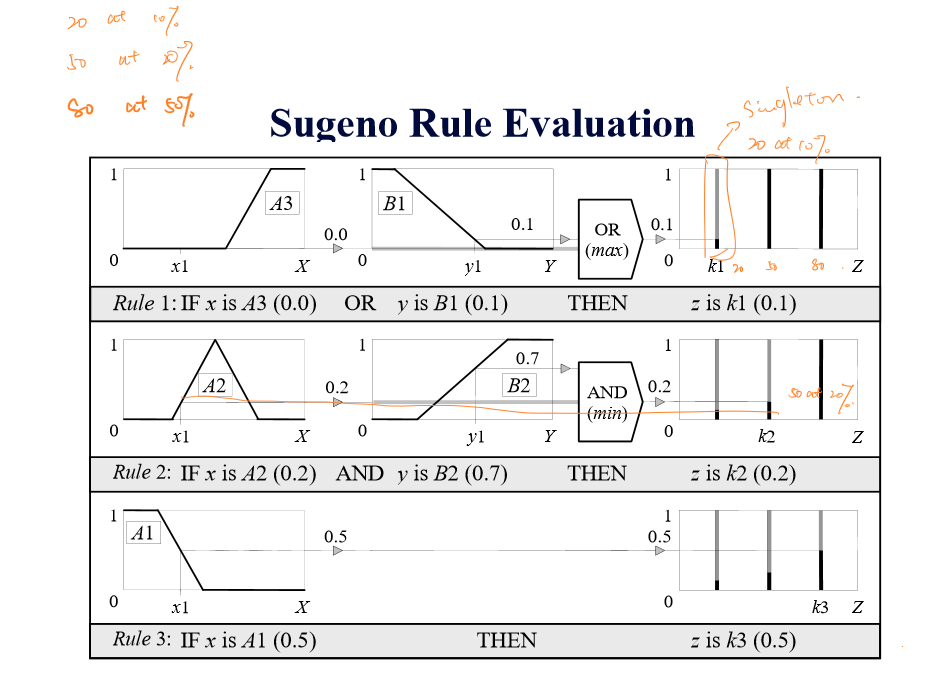
第三步聚合表示为：

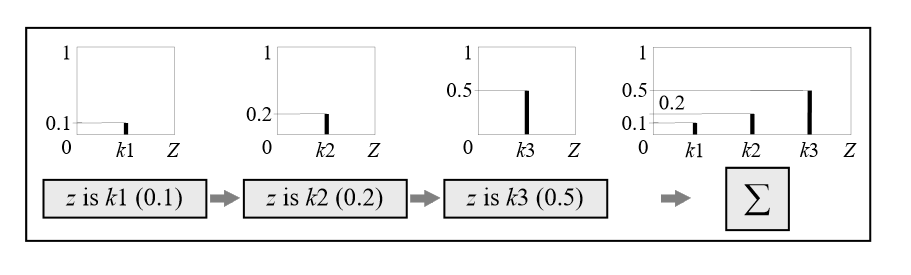
Sugeno模糊推理常常使用加权平均值来进行逆模糊化：
\[WA=\frac{∑k_i×μ_Z(K_i)}{∑μ_Z(k_i)}\]

方法评价

在获取专家知识时常常使用Mamdani方法，这种方法可以用更加直接、更加符合人类直觉的方式来描述专家的意见。但是其计算量更大。
Sugeno方法的计算效率高，可以与优化算法和自适应技术协同工作。这种方法在控制问题、尤其是在动态非线性系统研究领域比较有吸引力。

模糊运算

模糊集与实数的运算

• 倍数
  假定实数\(a\)与模糊集\(A\)，有： \[aA=\{aμ_A(x)\}\]
• 幂
  假定实数\(a\)与模糊集\(A\)，有： \[A^a=\{[μ_A(x)]^a\}\]

模糊关系

模糊关系用于表示两个模糊变量之间的关系强度。假设模糊变量\(X\)对应模糊集\(A\),模糊变量\(Y\)对应模糊集\(B\)，两者之间的关系强度可以用笛卡尔积(Cartesian Product)表示：
\[μ_{A×B}(x_i,y_j)=min(μ_A(x_i),μ_B(y_j))\] 即模糊集\(A\)中的每一个模糊变量\(X\)的个体\(x_i\)的隶属度\(μ_A(x_i)\)都要与模糊集\(B\)中模糊变量\(Y\)所有的个体\(y_j\)的隶属度\(μ_B(y_j)\)求最小值。最终得到一个关系矩阵\(R\)，其表示了模糊集\(A\)中的每一个模糊变量\(X\)的个体\(x_i\)与模糊集\(B\)中模糊变量\(Y\)每一个个体\(y_j\)的关系强度。
下图展示了一个模糊关系的计算例子：

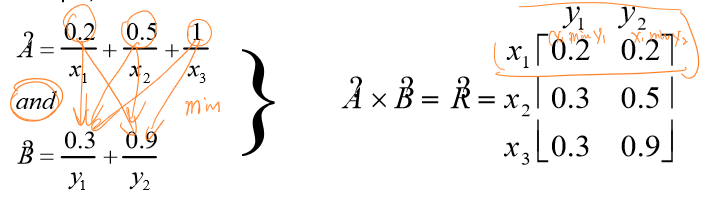
间接关系

如果模糊变量\(X\)与\(Y\)存在模糊关系\(R\),模糊变量\(Y\)与\(Z\)存在模糊关系\(S\)，那么可以借助模糊变量\(Y\)推导出模糊变量\(X\)与\(Z\)的关系\(F\):
\[F=R∘S\] 其中的\(∘\)代表了两种算子：
- max-min算子
\[μ_F(x_i,z_k)=max[min(μ_R(x_i,y_j),μ_S(y_j,z_k))]\] 即关系矩阵\(R\)的每一行与关系矩阵的\(S\)每一列对应元素取最小值后再取行列计算结果中的最大值。

- max-product算子
\[μ_F(x_i,z_k)=max[μ_R(x_i,y_j)·μ_S(y_j,z_k)]\] 即关系矩阵\(R\)的每一行与关系矩阵的\(S\)每一列对应元素相乘后再取行列计算结果中的最大值。

展开原则

展开原则(principle)描述了从一个模糊集\(A\)到另一个模糊集\(B\)的映射。
假设存在映射关系\(A→B:f(x)\)，\(A=\frac{μ_A(x_1)}{x_1}+\frac{μ_A(x_2)}{x_2}+...+\frac{μ_A(x_n)}{x_n}\)，有\(y_i=f(x_i)\)，那么有：
\[B=f(A)=\frac{μ_A(x_1)}{y_1}+\frac{μ_A(x_2)}{y_2}+...+\frac{μ_A(x_n)}{y_n}\] 如果计算后存在有\(y\)值相同的项，那么该\(y\)值对应的隶属值为这些项中最大的隶属值：
\[μ_B(y)=maxμ_A(x)\]

模糊集间的四则运算

对于两个模糊集\(A\)和\(B\)，分别对应模糊变量\(X\)和\(Y\)，其四则运算\(∘\)(\(∘∈\{+,-,×,÷\}\))的结果表示为：
\[\begin{aligned} F(A∘B)=&\left[\frac{min[μ_A(x_1),μ_B(y_1)]}{x_1∘y_1}+\frac{min[μ_A(x_1),μ_B(y_2)]}{x_1∘y_2}+...+\frac{min[μ_A(x_1),μ_B(y_n)]}{x_1∘y_n}\right]\\&+\left[\frac{min[μ_A(x_2),μ_B(y_1)]}{x_2∘y_1}+...+\frac{min[μ_A(x_2),μ_B(y_n)]}{x_2∘y_n}\right]+...+\left[\frac{min[μ_A(x_n),μ_B(y_1)]}{x_n∘y_1}+...+\frac{min[μ_A(x_n),μ_B(y_n)]}{x_n∘y_n}\right] \end{aligned}\] 简单来说即“两两配对，下面相加/减/乘/除，上面取最小”。
如果计算后存在有\(x_i∘y_j\)值相同的项，那么该\(x_i∘y_j\)值对应的隶属值为这些项中最大的隶属值：
\[μ_F(x_i∘y_j)=max\{min[μ_A(x_i),μ_B(y_j)]\}\] 下图展示了一个计算例子：

自适应神经模糊系统

模糊推理系统非常适于表示模糊的经验和知识，但缺乏有效的学习机制；神经网络虽然具有自学习功能，却又不能很好的表达人脑的推理功能。基于自适应神经网络的模糊推理系统ANFIS(ANFIS，Adaptive Network-based Fuzzy Inference System)将二者有机的结合起来，既发挥了二者的优点，又弥补了各自的不足。自适应神经网络模糊系统其中一个十分重要的应用，就是在信号处理和控制中消除噪声或干扰。

结构

自适应神经模糊系统只有5层结构，如下图所示：

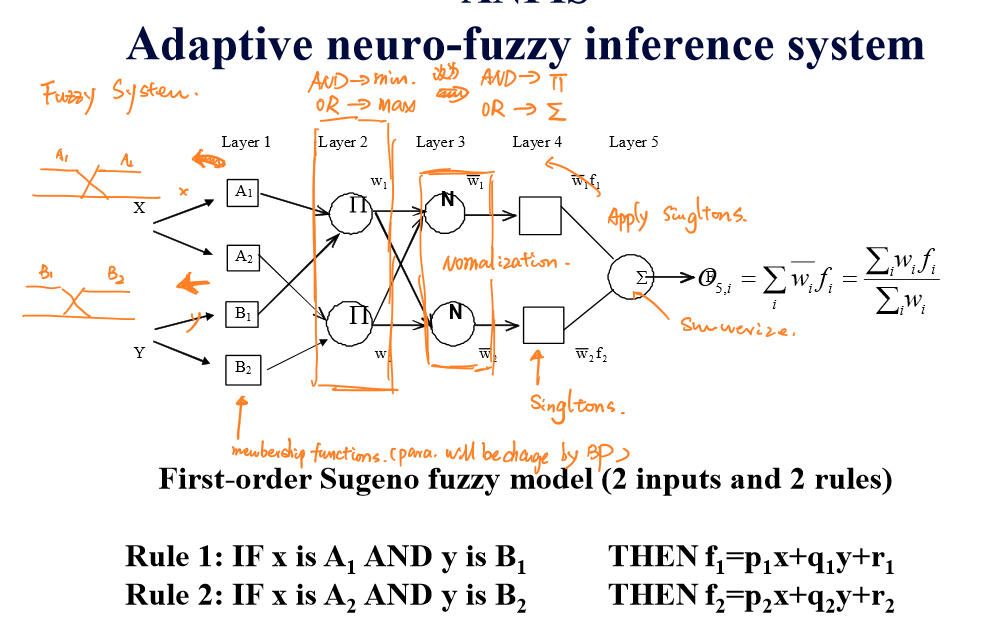
模糊层

第一层是模糊层，模糊层的每个节点带有一个隶属值函数：
\[O_{1,i}=μ_{A_i}(x),i=1,2\] \[O_{1,i}=μ_{B_i}(y),i=3,4\] 输入变量进入第一层后通过每个节点后将被各节点的隶属值函数转换为隶属值。
原始的自适应神经模糊系统第一层采用Sigmoid函数作为隶属值函数：
\[μ_A(x)=\frac{1}{1+|\frac{x-c_i}{a_i}|^{2b_i}}\] \[μ_B(y)=\frac{1}{1+|\frac{y-c_i}{a_i}|^{2b_i}}\]

运算层

这一层实现前提部分的模糊集的运算。在这一层中的每个结点都是固定结点，它的输出是所有输入信号的代数积。每个结点的输出表示一条规则的激励强度，本层的结点函数还可以采用取小、有界积或强积的形式。通常采用AND运算。
\[O_{2,i}=∏_{j=1}^nμ(x_j)=w_i\]

归一化层

第三层将第二层的输出\(w_i\)进行和归一化处理：
\[O_{3,i}= \overline{w_i} =\frac{w_i}{∑_jw_j}\]

结果层

这一层将归一化的权重应用到结合的单例项\(f_i\)中：
\[O_{4,i}=\overline{w_i}f_i=\overline{w_i}(p_ix+q_iy+r_i)\] 其中的两个单例项合并的结果：\(p_ix+q_iy+r_i\)中的系数需要通过反向传播找到。

逆模糊层

第五层是输出层，其将第四层的输出进行逆模糊化。逆模糊化的方法常常采用质心：
\[\hat{F}=O_{5,i}=∑_i\overline{w_i}f_i=\frac{∑_iw_if_i}{\sum_iw_i}\]

反向传播

自适应神经模糊系统的学习过程同样使用了基于梯度下降的反向传播。这是一种监督学习方法。
在ANIFS中，真实值和预测值的差表示为： \[δ=(\hat{F}-F)^2\] 其中\(F\)为真实值。
ANIFS系统中的参数\(a\)、\(b\)、\(c\)的更新公式为：
\[a:=a-η\frac{∂δ}{∂a}\] 输出层的梯度表示为：
\[δ_o=\frac{∂δ}{∂(x,y,...)}\]