无序变量的基本相关性分析方法和Python实现

概述

相关性(correlation analysis)是根据数据判断两个变量之间的变化关系是否随机的统计性质。和灵敏度分析不同，相关性检验主要是基于统计数据本身而非数学模型，且只考虑变量之间的两两关系。
高尔顿(Francis Galton)作为相关性检验的发明者，确定了一套用于描述两个变量相关性的数学语言：以一个指数\(ρ\)的值表示两个变量的相关性：
如果\(0<ρ≤1\)，表明两个变量之间存在正向的相关性，所谓正向指的是两个变量的变化方向一致；如果\(ρ=0\)，则表明两个变量之间不具有任何相关性；如果\(-1≤ρ<0\)，表明两个变量之间存在负向的相关性，两个变量的变化方向相反。

范围	解释
\(0<ρ≤1\)	两个变量具有正向相关性
\(ρ=0\)	两个变量不具有任何相关性
\(-1≤ρ<0\)	两个变量具有负向相关性

所谓等级变量，是指变量具有程度的性质，且使用具有不同高低的等级进行区分的变量，比如肝硬化程度、服务满意度等等。与之相反概念的是无序变量，这样的变量在描述时不使用等级语言。
常用的两种无序变量的相关性分析是皮尔逊相关性分析(Pearson correlation analysis)和斯皮尔曼相关性分析(Spearman correlation analysis)。

协方差和皮尔逊相关性分析

协方差

在统计学上，两个随机变量\(X\)、\(Y\)的方差满足如下关系：
\[D(X±Y)=D(X)+D(Y)±2E[(X-E(X))(Y-E(Y))]\] 其中， \[\begin{aligned} E[(X-E(X))(Y-E(Y))]&=E(XY-XE(Y)-YE(X)+E(X)E(Y))\\ &=E(XY)-E(X)E(Y) \end{aligned}\] 当两个随机变量独立时，\(E(XY)=E(X)E(Y)\),有\(E[(X-E(X))(Y-E(Y))]=0\)，\(D(X±Y)=D(X)+D(Y)\)。
当两个随机变量不独立时，有\(E[(X-E(X))(Y-E(Y))]≠0\)。
因此，\(E[(X-E(X))(Y-E(Y))]\)可以认为是可以衡量两个随机变量之间在线性代数和统计学上是否具有独立性，换言之即是否具有线性相关性的标志。定义两个随机变量的协方差(covariance):
\[Cov(X,Y)=E[(X-E(X))(Y-E(Y))]\]

皮尔逊相关分析

皮尔逊相关分析则是对协方差定义的进一步拓展，对两个随机变量的协方差使用各自的方差进行归一化处理，如此将满足高尔顿提出的相关性的数学描述：
\[ρ=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\] 进一步地，如果将\(X\)、\(Y\)的期望和方差进一步分解，有：
\[Cov(X,Y)=∑_{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})\] 同时\(D(X)=∑_{i=1}^n(x_i-\overline{X})^2\)、\(D(Y)=∑_{i=1}^n(y_i-\overline{Y})^2\)，定义统计学上的样本皮尔逊相关分析系数：
\[r=\frac{∑_{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})}{\sqrt{∑_{i=1}^n(x_i-\overline{X})^2}\sqrt{∑_{i=1}^n(y_i-\overline{Y})^2}}\]

代码实现

其在Python中的实现需要借用numpy库实现求和和列表相乘：

def pearson_correlation(X: 'lists', Y: 'lists')->['float']:
    x = np.array(X)
    y = np.array(Y)
    n = len(X)
    sum_xy = np.sum(np.sum(x * y))
    sum_x = np.sum(np.sum(x))
    sum_y = np.sum(np.sum(y))
    sum_x_square = np.sum(np.sum(x * x))
    sum_y_square = np.sum(np.sum(y * y))
    # pearson coefficient
    pearson = (n * sum_xy - sum_x * sum_y) / np.sqrt(
        (n * sum_x_square - sum_x * sum_x) *
        (n * sum_y_square - sum_y * sum_y))
    return pearson

当然，如pandas、scipy.stats之类的库中也有相关的函数可以实现皮尔逊相关系数。比如data.corr('pearson')或者stats.pearsonr(data.X,data.Y)。

由于皮尔逊相关系数本质上就是归一化的协方差，因此皮尔逊相关系数只能衡量两个随机变量之间是否具有线性相关性。

斯皮尔曼相关性分析

为了解决皮尔逊相关系数的局限性，斯皮尔曼(C Spearman)引入了等级相关的概念，并且阐述了其优点。斯皮尔曼相关性分析中，两个随机变量的统计样本通过对等级化取消了数据的直接相关性。所谓等级化\(R(·)\)是指原有的数据点按照相对大小由高到低排列，并用排序序号替换原有的统计数据。经过等级化后的随机变量进行皮尔逊相关性分析: \[r_s=\frac{∑_{i=1}^n(R(x_i)-\overline{R(X)})(R(y_i)-\overline{R(Y)})}{\sqrt{∑_{i=1}^n(R(x_i)-\overline{R(X)})^2}\sqrt{∑_{i=1}^n(R(y_i)-\overline{R(Y)})^2}}\] 如此皮尔逊相关性分析衡量的就是两个等级变量的相关性。由于等级变量只会表示数据的相对大小，因此这样的结果是皮尔逊相关分析只会体现出两个随机变量的单调相关性。
因此，斯皮尔曼相关性分析衡量了两个随机变量的单调相关性。

当所有的等级都是正整数时，\(r_s\)可以简化为：
\[𝑟_𝑠=1−\frac{6∑_{i=1}^n𝑑_𝑖^2}{𝑛(𝑛^2−1)}\] 其中\(d_i\)是第\(i\)个样本\((x_i,y_i)\)的等级差：\(d_i=R(x_i)-R(y_i)\).

如果多个样本具有相同的值：\(x_a=x_b=x_c=...x_z\)，那么这些样本的等级将被平均化：
\[R(x_a)=\frac{R(x_a)+R(x_b)+...+R(x_z)}{N_{same}}\]

代码实现

首先将两个输入的随机变量数据从大到小进行排序，并检测是否存在值相同的样本数据，如果有则将这些样本点的等级平均化。

# order two lists
def sort_list(X):
    X_sorted = sorted(X,reverse=True)
    X_d = []
    # exam whether this value is repeated
    for i in X:
        if X_sorted.count(i)==1:
            X_d.append(X_sorted.index(i))
        else:
            # if the value is repeated, the rank will be the average rank for the repeated number
            X_d.append(X_sorted.index(i)/X_sorted.count(i))
    return X_d

带入公式：

# find the difference of ranks of two data, d , then square and sum
sum_d_square = 0
for j in range(len(X_d)):
    d = X_d[j] - Y_d[j]
    sum_d_square = sum_d_square + d*d
# spearman coefficent 1-[(6*\sum d^2)/(n(n^2-1))]
spearman = 1-(6*sum_d_square/(n*(n*n-1)))

完整代码如下：

def spearman_correlation(X:'list',Y:'list'):
    # order two lists
    def sort_list(X):
        X_sorted = sorted(X,reverse=True)
        X_d = []
        # exam whether this value is repeated
        for i in X:
            if X_sorted.count(i)==1:
                X_d.append(X_sorted.index(i))
            else:
                # if the value is repeated, the rank will be the average rank for the repeated number
                X_d.append(X_sorted.index(i)/X_sorted.count(i))
        return X_d

    # exam the length of two list
    if len(X)==len(Y):
        n = len(X)
        X_d = sort_list(X)
        Y_d = sort_list(Y)

        # find the difference of ranks of two data, d , then square and sum
        sum_d_square = 0
        for j in range(len(X_d)):
            d = X_d[j] - Y_d[j]
            sum_d_square = sum_d_square + d*d
        # spearman coefficent 1-[(6*\sum d^2)/(n(n^2-1))]
        spearman = 1-(6*sum_d_square/(n*(n*n-1)))
    else:
        print('Length unequal')
        spearman = None
    return spearman

当然，如pandas、scipy.stats之类的库中也有相关的函数可以实现斯皮尔曼相关系数，比如data.corr('spearman')或者stats.spearmanr(data.X,data.Y)。

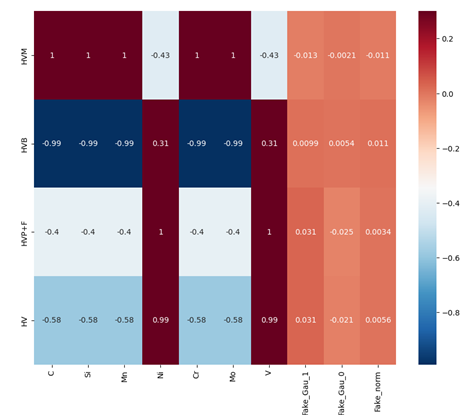
多维数据还可以使用seabon.heatmap将相关性检验的结果表示为热力图，例如：

seaborn.heatmap(hardness_data,vmax=0.3,annot=True,cmap="RdBu_r")
plt.show()