生成对抗网络

Generative Adversarial Nets, Ian J Goodfellow et al, 2014.
Conditional Generative Aversarial Nets, Mehdi Mirza et al, 2014.

简介

问题动机

深度学习的意义是挖掘人工智能应用领域不同种类的数据集的丰富的、层次化的概率统计分布模型。目前，深度学习领域最成功的研究已经包括了鉴别模型(discriminative model)——通常是将高维度，丰富的感知输入映射到类别标签的模型。判别模型中常常使用反向传播和dropout算法以及分段线性单元（piecewise linear unit），它们具有特别良好的梯度。
人工智能的另一种模型是生成模型(generative model)，即根据数据集分布特征生成新数据的人工智能模型。深度的生成模型(generative model)在研究领域的影响不大的原因有二：

• 应用最大似然估计和相关策略时出现了的概率计算困难
  
• 在生成上下文中难以应用利用分段线性单元的优势
  

  使用ReLU函数作为激活函数的神经元是一种典型的分段线性单元。ReLU函数可以表示为：
  \[f(x)=max(0,x)\] ReLU函数的优点是计算量小，收敛速度快。缺点是当较大梯度通过ReLU神经元，更新参数之后，这个神经元不会对任何数据有激活现象，神经元梯度将永远为0.

网络框架

本文提出了一种新的可以避免这两种问题的新的生成模型估计程序，称为生成对抗网络(GAN, generative adversarial nets)。这种对抗网络中，除了生成模型外，还有一个与之对抗的鉴别模型：鉴别模型，又称为鉴别器(distriminator)学习鉴别某个样本来自生成模型，又称为生成器(generator)的概率分布（是生成模型所生成的样本），还是来自原数据集的概率分布（是原数据集中真实存在的样本）。
上述过程可以将生成器比作生产假钞的造假者(counterfeiter)、鉴别器比作识别假钞的警察。造假者需要尽可能的将假钞制作得逼真到使警察无法识别，而警察则需要不断练习以鉴别真钞和假钞。
最终，如果造假者造出了警察无法识别的假钞，那么造假者将赢得这场竞争。即当鉴别模型无法鉴别样本源头时，算法终止。

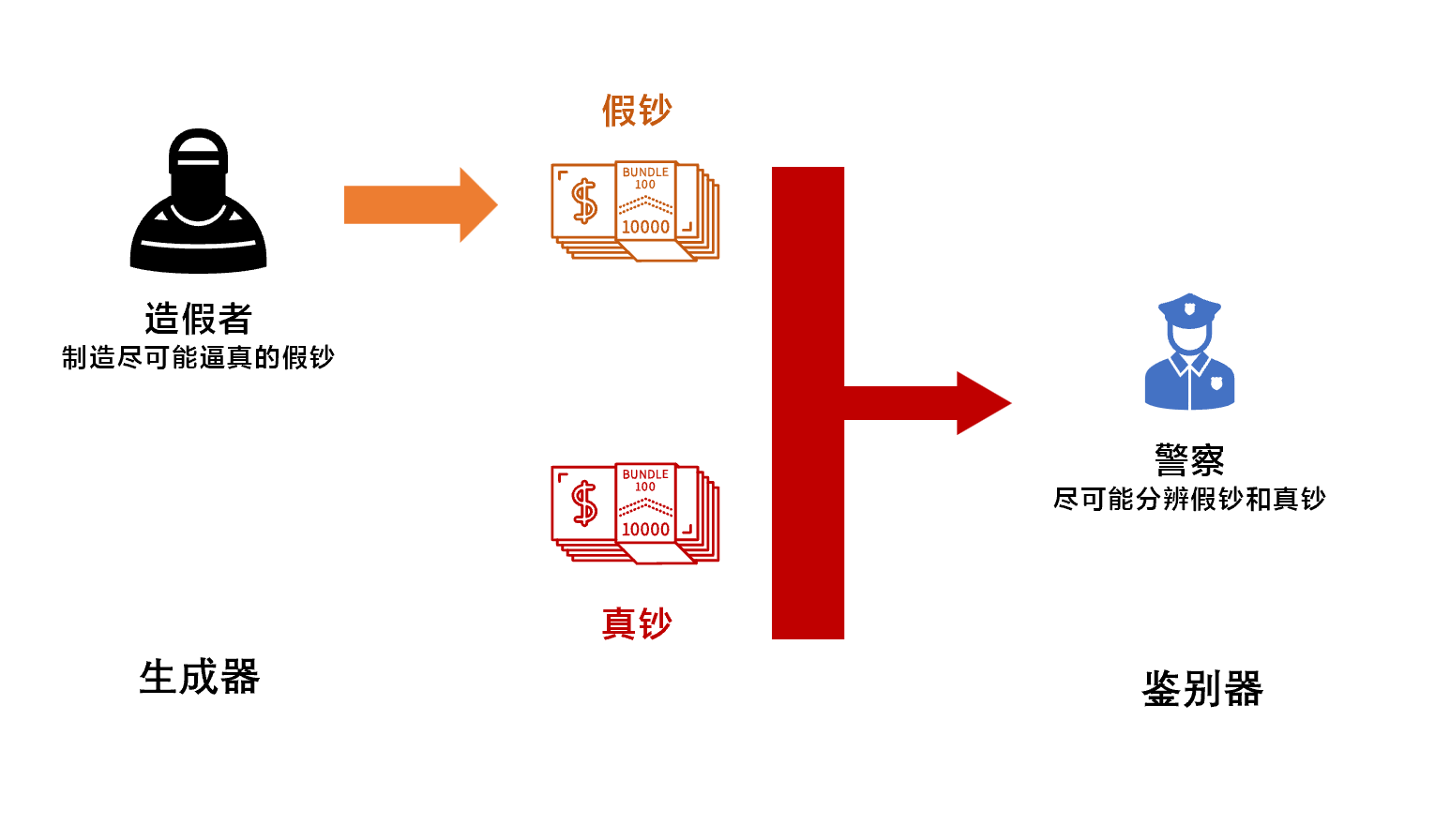
整个网络框架可以用多种模型和优化算法实现。本文中生成器和鉴别器的结构都是多层感知机(multi-layer perceptron)，其中生成器的输入是随机噪声。两者的训练方式均采用反向传播和dropout算法，并仅使用正向传播从生成模型中进行采样。训练过程中不需要任何近似推断(approximate inference)和马尔科夫链(Markov chain)。

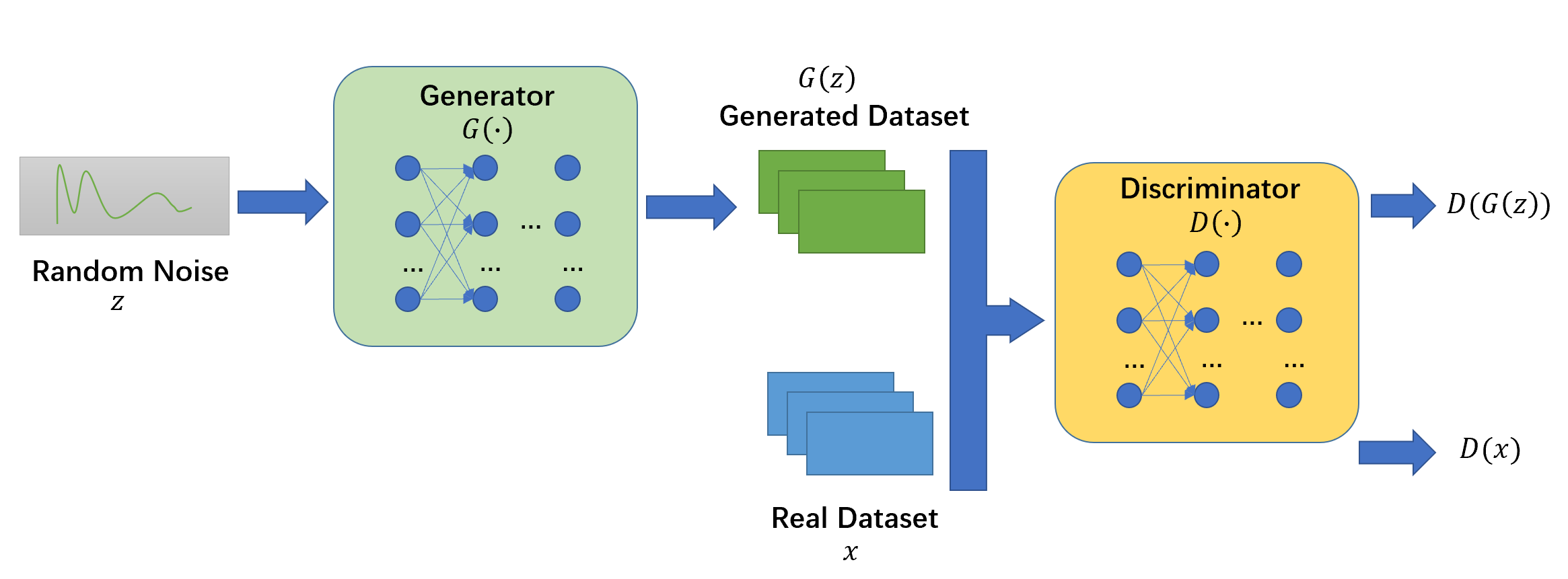
既有方法

大多数有关深度生成模型的工作都集中在提供一个概率分布函数的参数规范的模型上。然后可以通过最大化对数似然来训练模型。文章中列举出了几种比较有代表性的生成模型，如下表所示：

名称	概要	缺点
玻尔兹曼机 Boltzmann machine	模型的相互作用表示为没有归一化的势函数的乘积，通过对随机变量的所有状态进行求和或者定积分进行归一化	梯度不可追踪 混合对依赖于马尔科夫蒙特卡洛方法的学习算法造成了极大的问题
深度信念网络 DBN, deep belief networks	含有一个无向层和几个有向层的混合模型	无向模型和有向模型都存在计算困难
噪声对比估计 NCE,noise-contrastive estimation	需要设定一个判别训练标准以拟合生成模型，生成模型本身用于辨别从固定分布的噪声中生成的样本	由于使用了固定分布的噪声，学习速率在学习模型（甚至是相当一小部分数据）之后显著变慢
生成随机模型 GSN, generative stochastic network	从所需的分布中抽取样本训练生成器，可以看做是参数化的马尔科夫链	需要计算马尔科夫链

而对抗网络框架不需要马尔科夫链进行采样。由于对抗网络在训练生成器的过程中不需要循环反馈，生成器的训练只是单次的，梯度下降的更新速率较慢，一定程度上避免了分段线性单元出现过早收敛的问题。从而可以更好的利用分段线性单元、提高反向传播的算法性能。

但是这样的梯度下降方式也会导致GAN的收敛非常不稳定。

训练过程

交叉熵

信息论中以消息中包含的未确定事件的概率来衡量信息的大小，称为信息量。信息熵是用来衡量消息有效率的指标，信息熵表示消息中平均含有的信息量： \[H(P)=∑P(x_i)log_2\frac{1}{P(x_i)}\] 其意义是表示随机变量\(X\)如果按照其真实的概率分布\(P(x_i)\)进行编码，所得到的编码长度的期望，是理想最佳状态下的编码长度。
然而如果采用某种错误分布\(Q(x_i)\)为该随机变量进行编码，那么此时编码长度的期望为：
\[H(P,Q)=∑P(x_i)log_2\frac{1}{Q(x_i)}\] 该式子\(H(P,Q)\)称为交叉熵。

Kullback-Leibler散度/KL散度

Kullback-Leibler散度用于衡量随机变量\(X\)在非理想最佳状态下编码信息损失。根据交叉熵（非理想编码）和信息熵（理想编码）的定义，定义Kullback-Leibler散度为随机变量\(X\)的交叉熵与信息熵的差：
\[KL(p||q)=∑p(x)log(p(x))-∑p(x)log(q(x))=∑_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)})\] KL散度在\(p(x)\)和\(q(x)\)相同时取到最小值0，两个概率分布越相似，则KL散度越小。

二元分类器、最大似然估计与二元交叉熵

对于处理数据集\(D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)的二元分类器，令其分类结果/观察结果\(y∈\{0,1\}\)，即观察结果不是\(y=0\)就是\(y=1\)——这符合伯努利分布的性质。那么分类器假设观察结果\(y=1\)的概率为：
\[P_θ(y=1)=θ,θ∈[0,1]\] 那么有\(P_θ(y=0)=1-θ\)，综合这两个式子，可以得到\(y\)的（边缘）概率密度函数服从伯努利分布：
\[p_θ(y)=θ^y(1-θ)^{1-y}\] 此时可以将数据集标签\(y_1,y_2,...,y_N\)视为总体\(Y\)中的样本，利用数据集中每一个数据的真实结果\(y_i\)对分类器参数\(θ\)进行最大似然估计，那么\(y_1,y_2,...,y_N\)的联合概率密度函数表示为每一个独立样本\(y_i\)边缘概率密度函数的乘积：
\[\mathcal{L}(θ)=∏_{i=1}^Np_θ(y_i)=∏_{i=1}^Nθ^{y_i}(1-θ)^{1-y_i}\] 取对数以便于求得使\(\mathcal{L}(θ)\)最大时的\(θ\)：
\[l(θ)=log(\mathcal{L}(θ))=∑_{i=1}^Nlog[θ^{y_i}(1-θ)^{1-y_i}]=∑_{i=1}^N[y_ilogθ+(1-y_i)log(1-θ)]\] 上述式子称为二元交叉熵公式(binary cross-entropy)，表示所有样本的交叉熵之和。

损失函数

设对抗网络框架中含有参数\(θ_g\)的生成器表示为\(G(z;θ_g)\);含有含有参数\(θ_d\)的器表鉴别示为\(D(x;θ_d)\)，表示\(x\)为真实样本的概率为\(D(x)\)。GAN的目标是让生成器生成足以欺骗判别器的样本。从数学角度将，GAN希望生成样本和真实样本拥有相同的概率分布，也可以说生成样本\(G(z)\)和真实样本\(x\)拥有相同的概率密度函数，即：
\[p_G(x)=p_{data}(x)\] 接下来就只需要定义一个优化问题，找到一个\(G\)满足上述式子即可。
对于GAN的鉴别器，其本质是一个二元分类器，因此GAN借鉴了二元交叉熵公式。其损失函数表示为：
\[L=-\frac{1}{m}[y_ilogp_i+(1-y_i)log(1-p_i)]\] 其中第一项的作用是用来使正样本的识别结果尽量为1 ，第二项的作用是使负样本的预测值尽量为0。
根据之前介绍的对抗网络框架的结构，那么要求鉴别器能够将满足\(p_{data}(x)\)分布的真实样本\(x\)正确辨别出来，记为正样本“1”，有：
\[\mathbb{E}_{x\sim p_{data}(x)}log(D(x))\] 同时要求鉴别器能够将生成器用随机噪声\(z\)生成的样本\(G(z)\)正确辨别出来，记为负样本“0”，有：
\[\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z)))\] 综合上述推理，鉴别器的作用是将真实样本\(x\)正确记为1，将生成器用随机噪声\(z\)生成的样本\(G(z)\)正确记为0，那么鉴别器的作用可以表示为下列式子：
\[V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}log(D(x))+\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z)))\] 可以发现，\(V(D,G)\)越大，鉴别器的工作越好，越容易分辨样本是生成的还是原本数据集中的；\(V(D,G)\)越小，鉴别器的工作越差，越不容易分辨样本是生成的还是原本数据集中的。那么对于鉴别器而言，其优化问题应当是找到使得\(V(D,G)\)最大的\(D\):
\[\mathop{max}\limits_{D}V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}log(D(x))+\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z)))\] 对于生成器，GAN中应用了悲观理论：考虑对手处于最佳状态下击败对手。具体而言，GAN中的生成器需要在鉴别器处于最佳状态下，尽可能生成让鉴别器无法识别的样本。换言之，即最小化式子\(\mathop{max}\limits_{D}V(D,G)\)，即\(\mathop{min}\limits_{G}[\mathop{max}\limits_{D}V(D,G)]\)——这样的算法称为最小-最大算法(minimax algorithm)，写作：
\[\mathop{min}\limits_{G}\mathop{max}\limits_{D}V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}log(D(x))+\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z)))\]

算法运行

GAN的学习分为两个内外两个循环：对于每一次迭代（外循环），需要\(k\)步优化鉴别器\(D\)使其处于目前的最优状态，然后再仅一步优化生成器。如此，鉴别器\(D\)可以保持在它的最优结果附近，而生成器\(G\)缓慢改变。
具体过程如下所示：

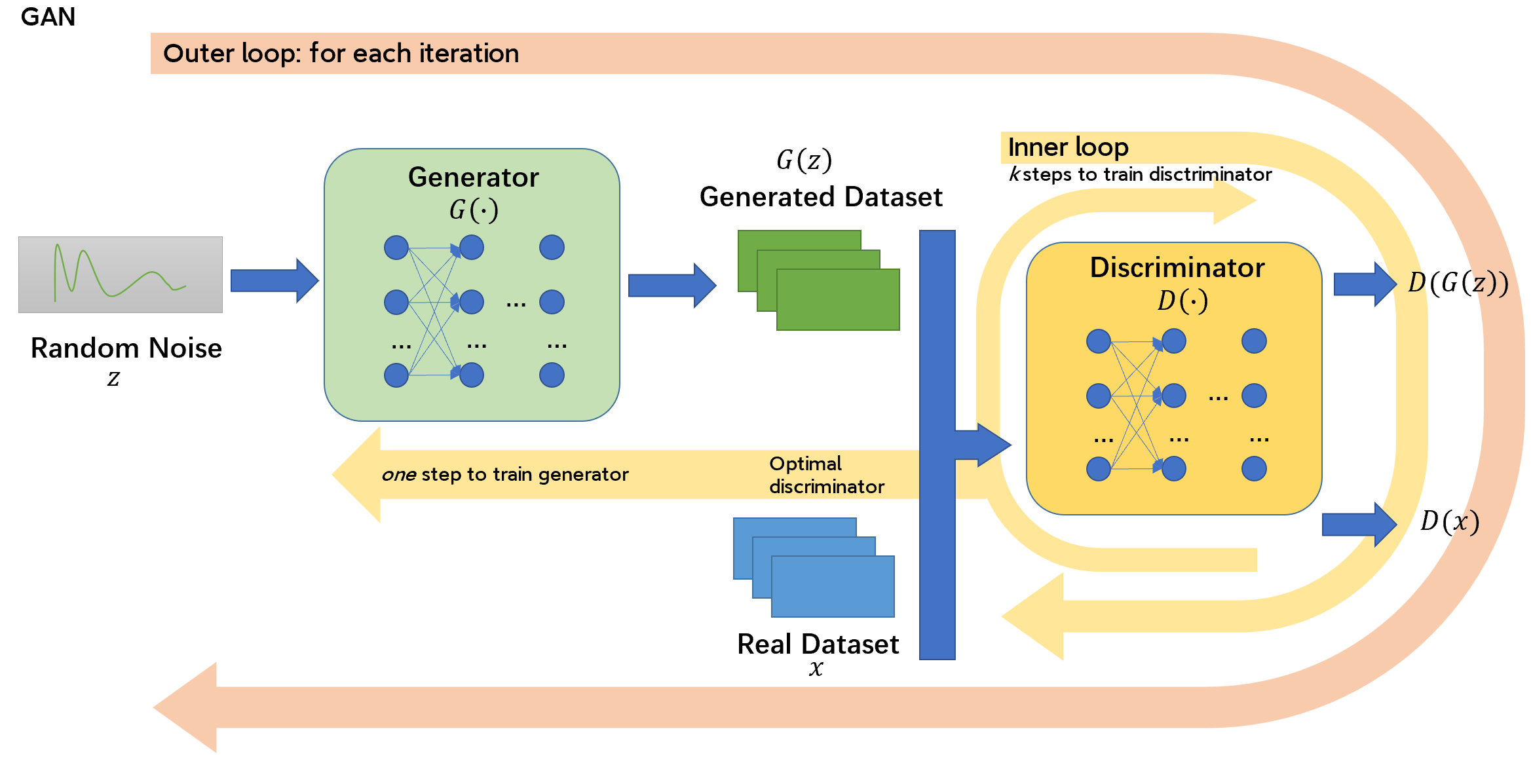
algorithm

for number of training iterations do  for \(k\) steps do   在噪声分布\(p_g(z)\)中采样\(m\)个样本：\(\{z^{(1)},...,z^{(m)}\}\)   在真实数据分布\(p_{data}(x)\)中采样\(m\)个样本：\(\{x^{(1)},...,x^{(m)}\}\)   使用梯度上升算法更新辨别器梯度：\[▿_{θ_d}\frac{1}{m}\sum_{i=1}^m[logD(x^{(i)})]+log(1-D(G(z^{(i)})))]\]  end for  在噪声分布\(p_g(z)\)中采样\(m\)个样本：\(\{z^{(1),...,z^{(m)}}\}\)  使用梯度下降算法更新生成器梯度：\[▿_{θ_g}\frac{1}{m}\sum_{i=1}^mlog(1-D(G(z^{(i)})))\] end for

整个算法的实质是构造一个鞍型函数，并寻找其鞍点。该鞍形函数的一侧为凸函数(鉴别器的鉴别能力)，另一侧为凹函数（生成器的生成能力）。如下图所示：

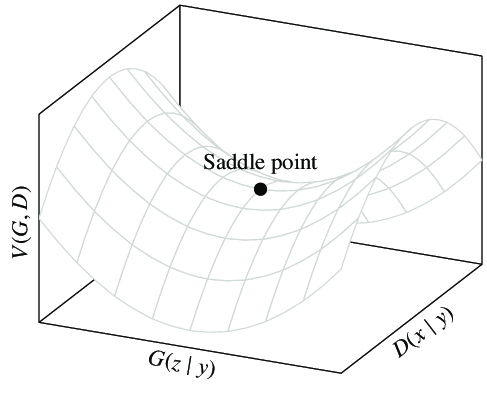
事实上，该算法有可能无法为生成器\(G\)的学习提供足够的梯度。在训练早期，生成器\(G\)还比较弱，不足以模仿数据集中的数据时，鉴别器\(D\)可以很轻松地鉴别出生成数据。此时\(log(1-D(G(z)))\)处于接近1的饱和状态。因此为了避免这种情况，可以在训练生成器时最大化\(log(D(G(z)))\)，这种策略可以在训练早期为生成器\(G\)提供足够的精度。
设\(p_{data}\)表示数据集的数据分布，\(p_g\)表示生成器生成的数据的数据分布。整个训练过程中鉴别器、生成器产生的分布如下图所示：

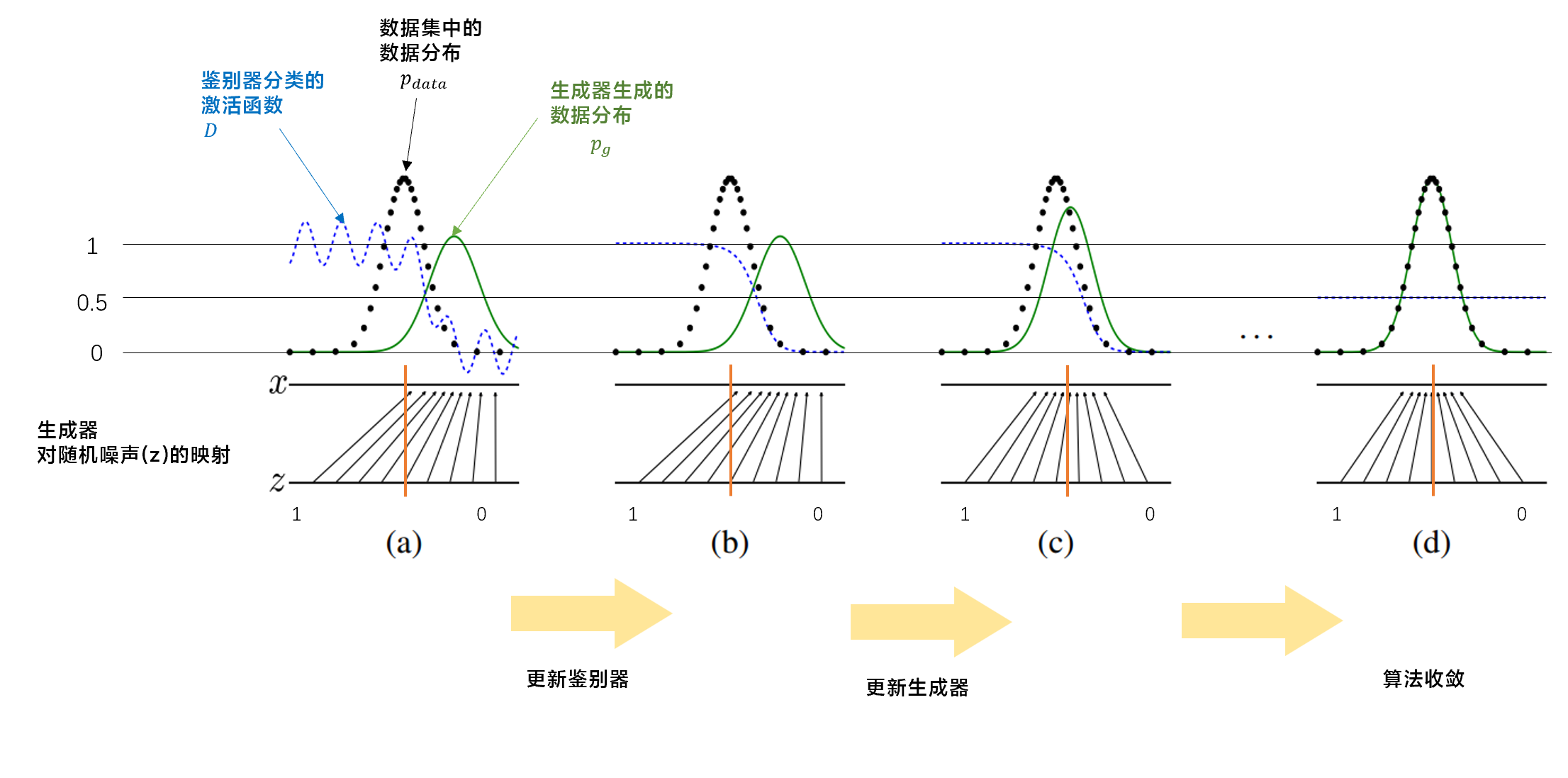
如图所示：

• a): 首先考虑训练至接近收敛的情况，此时\(p_g\)已经与\(p_{data}\)较为相似，鉴别器\(D\)是一个较为准确的二分类器。此时生成器并不完美，它对随机噪声的映射没有贴合真实的数据分布\(p_{data}\)。
  
• b): 在一次迭代中，首先对鉴别器进行循环学习，使鉴别器性能达到最优。
  
• c): 然后根据最优鉴别器的参数，生成器将做出调整，使其产生的数据分布更加接近真实的数据分布\(p_{data}\)。
• d): 随着算法迭代，理想情况下，最终生成器学习到了真实的数据分布，此时\(p_g=p_{data}\)。在这种情况下，鉴别器将无法识别两类样本，对两类样本的识别概率如同抛硬币一样，都是50%。

数学证明

最优判别器

GAN在一轮迭代中的第一步是对于任何给定的生成器\(G\)，优化鉴别器\(D\)。对于某个给定的生成器\(G\)，对应的最优化鉴别器\(D^*\)为：
\[D^*_G(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\] 证明方法如下：
将\(V(D,G)\)中含有的数学期望进行展开：
\[V(D,G)=∫_xp_{data}(x)log(D(x))dx+∫_zp_z(z)log(1-D(g(z)))dz\] 根据LOTUS定理（Law of the Unconscious Statistician），统一符号，有： \[V(D,G)=∫_xp_{data}(x)log(D(x))+p_g(x)log(1-D(x))dx\]

LOTUS定理
计算一个函数的期望时，可以不知道这个函数的分布。取而代之的是可以知道一个简单的分布，以及从简单分布到当前分布的映射即可。
即： \[\mathbb{E}_{p(x;θ)}[f(x)]=\mathbb{E}_{p(ϵ)}[f(g(ϵ;θ))]\] 在本文中存在映射\(z→x\)，对应映射法则为\(g(z)\)。因此可以做如上的替换。

对于形如"\(alog(y)+blog(1-y),y∈[0,1]\)"的函数，其最大值在\(y=\frac{a}{a+b}\)上取得，对于上式，其最大值应当在\(D^*_G(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\)上取得。

最优生成器

对于固定的鉴别器\(D\)，当且仅当\(p_G=p_{data}\)时，才可以得到\(C(G)=max_DV(G,D^*)\)的最小值。 此时\(D^*=\frac{1}{2}\)，\(V(G,D^*_G)=-log4\)。证明过程如下：
\[\begin{aligned} C(G)&=max_DV(G,D^*)\\ &=∫_xp_{data}(x)log(\frac{p_{data}(x)}{p_{data}(x)+p_g(x)})+p_G(x)log(1-\frac{p_{data}(x)}{p_{data}(x)+p_g(x)})dx\\ &=∫_xp_{data}(x)log(\frac{p_{data}(x)}{p_{data}(x)+p_g(x)})+p_G(x)log(\frac{p_G(x)}{p_{data}(x)+p_g(x)})dx \end{aligned}\] 上述式子可以转化为：
\[C(G)=-log4+∫_xp_{data}(x)\left(log(2)+log(\frac{2p_{data}(x)}{p_{data}(x)+p_g(x)})\right)dx+∫_xp_G(x)log(\frac{2p_G(x)}{p_G(x)+p_g(x)}dx)\] 带入KL散度公式，得到：
\[C(G)=-log4+KL(p_{data}||\frac{p_{data}+p_G}{2})+KL(p_G|\frac{p_{data}+p_G}{2})\] 由于\(KL(p_{data}||\frac{p_{data}+p_G}{2})\)和\(KL(p_G|\frac{p_{data}+p_G}{2})\)总是非负的，因此\(C(G)≥-log4\)。 换言之，当且仅当\(KL(p_{data}||\frac{p_{data}+p_G}{2})=KL(p_G|\frac{p_{data}+p_G}{2})=0\)时存在\(C(G)\)的最小值，此时\(p_{data}=p_G\)。
当\(p_{data}=p_G\)时，\(D^*=\frac{1}{2}\)的意义是鉴别器判断一个样本来自数据集本身还是生成器生成的概率都是50%——这个结果等价于鉴别器判断一个样本的来源是完全的随机猜想，即鉴别器无法判断样本的来源。

一个快速证明最优生成器的方法是对\(V(D,G)\)去对数化：
即将原来的加减回归到乘除运算，有：
\[V_f(D,G)=D(x)[1-D(x)]\] 该函数在\(D(x)=\frac{1}{2}\)时取得最大值。
这个快速证明方法并不严谨，但是有助于简单理解上述数学证明的过程。

算法收敛性

如果G和D具有足够的容量，并且在算法1的每个步骤中，允许鉴别器达到其给定的最佳G，并更新以提高评估标准，使得趋近\(\mathop{min}\limits_{G}\mathop{max}\limits_{D}V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}log(D(x))+\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z)))\)。
证明：将\(V(G,D)= U(p_g,D)\)视为上述过程中关于\(p_g\)的函数且\(U(p_g,D)\)是对\(p_g\)的凸函数。\(U(p_g,D)\)且具有之前所证明的证明的唯一全局最优值，因此在\(p_g\)的更新足够小的情况下，\(p_g\)能收敛到\(p_x\)。

事实上，对抗网络通过函数\(G(z;θ_g)\)表示一系列有限的分布，并且而且通常优化的是\(θ_g\)而不是\(p_g\)本身，因此证明不适用。但是多层感知器在实践中的出色性能表明，尽管缺乏理论上的保证，它们还是可以使用的合理模型。

实验验证

论文中使用GAN和其他生成网络学习MINST、TFD等数据集。其中生成器网络使用了线性和sigmoid函数作为激活函数，鉴别器网络使用了maxout激活。并且dropout算法应用在鉴别器的训练上。
下表展示了使用Parzen window-based log-likelihood estimates评估方法得到的MINST和TFD数据集的标准差：

Model	MINST	TFD
DBN	138±2	1909±66
Stacked CAE	121±1.6	2110±50
Deep GSN	214±1.1	1890±29
本方法	225±2	2057±26

该表格可以简单理解为标准差越大，对数据集的拟合越精确。可以发现本方法中的对抗网络在对MINST和TFD数据集的学习中都体现出了较高的方差特性。
下图随机选取了使用GAN生成了样本并进行可视化。

最右边的列显示了邻近样本的最近训练示例，以证明该模型没有存储训练集。样本是公平的随机抽签，并非精心挑选。与大多数其他深层生成模型的可视化不同，这些图像显示了来自模型分布的实际样本，而不是给定隐藏单元样本的条件均值。此外，这些样本是不相关的，因为采样过程不依赖于马尔可夫链混合。 a）MNIST b）TFD c）CIFAR-10（全连接模型） d）CIFAR-10（卷积鉴别器和“反卷积”生成器））

评价

优点

• 学习过程中不需要马尔科夫链和推断学习，在反向传播中只需要梯度即可更新参数。
  
• 根据更新好的辨别器参数来训练生成器，而非根据数据集来训练生成器，这样训练过程中输入的样本并没有直接导入到生成器。这样的结构降低了计算量。
  
• 竞争网络可以生成一个非常尖锐的高方差分布，对于样本分布的拟合更加精确。然而基于马尔科夫链的方法为了混合模式需要一个模糊的分布。

除此之外，GAN使用了无监督学习，对数据集不需要标注。但是也同时意味着生成的样本类别是不可控制的。

缺点

在学习过程中必须要保证鉴别器\(D\)的学习率与生成器\(G\)有良好的同步。实际上，在没有更新鉴别器之前，生成器不能够学习过多，以避免“海奥维提卡现象”(Helvetica Scenario)：不管输入的随机噪声\(z\)的取值如何，生成器都会一直生成同样的样本（生成器通过不断生成此样本就能够一直骗过判别器，即判别器会将其判定为真实数据，因此生成器也就开始“偷懒”：一直源源不断地生成同样的数据样本），使得生成样本的多样性差。

条件生成对抗网络

在《Generative Adversarial Nets》一文最后，作者提出了对生成对抗网络的损失函数添加条件概率的可能性。在《Conditional Generative Adversarial Nets》一文中，作者详细地解释了这一可能的实现。

问题动机

对于原始的GAN来说，由于采用了无监督学习学习样本，因此生成器生成的样本类别是不可控制的。换言之，使用者无法指定生成器生成某一类样本。
同时，对于现有的多模型图像识别学习而言还存在着另外两个问题：

• 1. 随着数据集中含有图像的种类越来越广泛，如今的图像识别模型需要适应非常庞大的输出类别。
     
• 2. 现在的研究主要都是基于“一对一”的映射关系：比如一张图片对应某一个标注/类别。然而事实上一张图片可能对应多个标注和类别，不仅如此，不同用户对于同一张图片的描述也不尽相同，因此实际问题中通常含有的关系是“一对多”的映射关系，即一个图像对应多个描述。

对于问题a)，一个有效解决办法是使用自然语言处理算法，将不同用户对于同一张图片的描述转换为语义相同的词向量(words vector)，研究这些词向量与图像之间的关系。
对于问题b)，一个解决办法是使用有（多个）条件的概率生成模型，模型的输入是条件变量，从而使一对多的映射关系具象化为一个条件概率分布。

方法论及结果

因此，条件生成对抗网络CGAN中使用了带有条件概率的损失函数，并将条件设置为样本的标签/类别，从而将无监督学习转换为监督学习，就可以创造出可以生成指定样本的生成器，并且可以通过糅合多个条件实现“一对多”的映射表达。
CGAN对于生成器和鉴别器，都需要以条件概率的形式添加额外的信息\(y\)，\(y\)可以是任何对识别有帮助的信息(auxiliary information)，比如对于每个个体的标签，或者是经过自然语言处理之后的词向量集等等。\(y\)将作为条件进入到额外的输入层中：
对于生成器，\(y\)可以以某种具体的办法加入到随机噪声中进行“隐含表示”(hidden representation)，原始的GAN对加入的方法具有很高的兼容性。
对于鉴别器，\(x\)和\(y\)都会作为鉴别函数的输入变量。
现在的优化目标改写为：
\[\mathop{min}\limits_{G}\mathop{max}\limits_{D}V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}log(D(x|y))+\mathbb{E}_{z\sim p_{z}(z)}log(1-D(G(z|y)))\] 这就是CGAN的优化目标。和原始的GAN相比，其在函数表现上仅仅加入了一个条件\(·|y\)，然而由于\(y\)的多样性，大大拓宽了GAN的使用限制。现在，对于训练好的生成器\(G(z|y)\)，可以通过指定样本标签\(y\)来让生成器生成对应标签的样本。
CGAN的架构如下图所示：

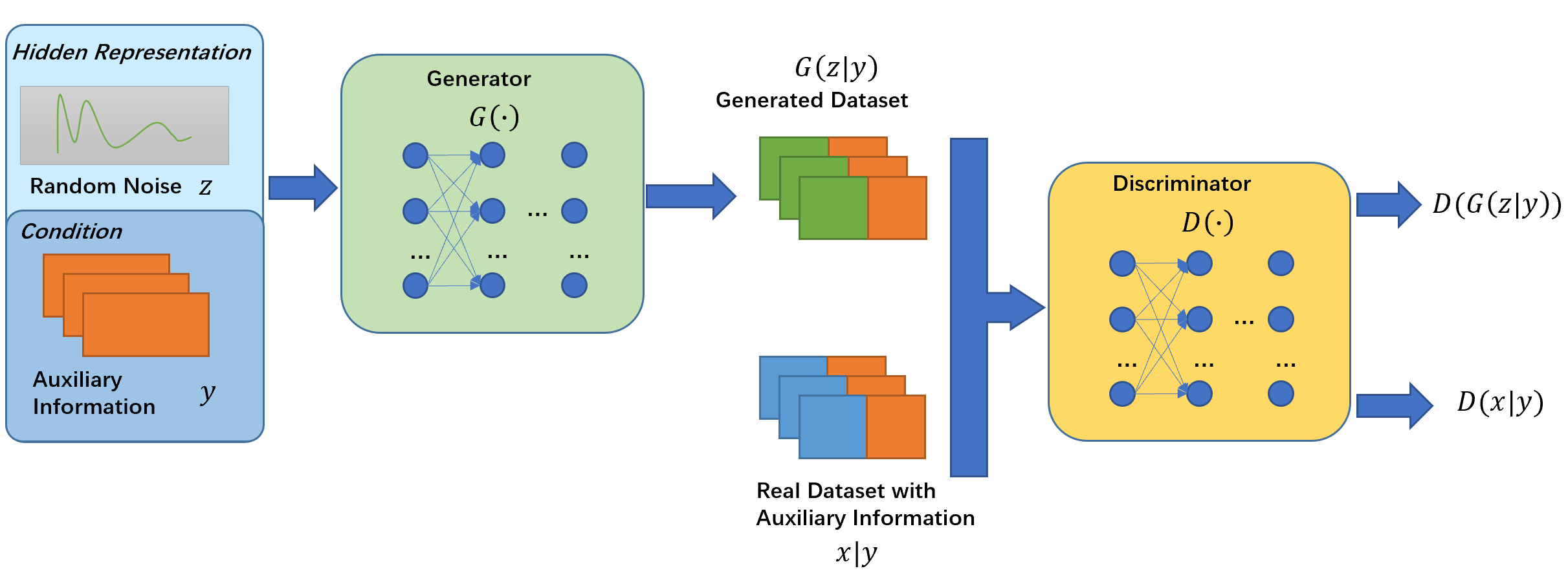
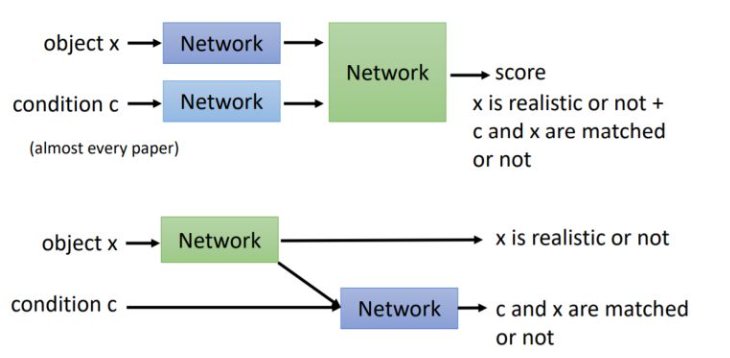
随着之后的演化，现在CGAN的鉴别器有两种结构，一种是将数据\(x\)和条件\(y\)（图中的\(c\)）分别经过一个网络处理后再融合为一个网络，对模型进行评价。另一种是使用一个网络评价\(x\)是来自生成的数据还是数据集，再使用另一个网络评价条件和数据是否吻合。

下图展示了使用CGAN的生成器生成的一些样本，这些样本指定了标签进行生成：