自适应遗传算法的Python实现

本文最后更新于 2023年12月12日 上午

自适应遗传算法：理论、Python实现和改进

M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms," IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, 1994, doi: https://doi.org/10.1109/21.286385.

问题动机

回顾：突变的效应

经典遗传算法中突变存在两种效应：
- 积极效应：突变可以在进化陷入局部最优解时通过施加干扰使得整个进化跳出局部最优解。
- 消极效应：突变的随机扰动会破坏个体中原本搜索好的信息。

在经典遗传算法中需要精确地设置突变概率以平衡突变的积极和消极效应。

适应度下降

经典遗传算法在运行过程中存在一个严重的问题，随着进化的轮数不断增加，现有种群中的适应度会不增反降。这种现象我将其称之为“适应度下降”。

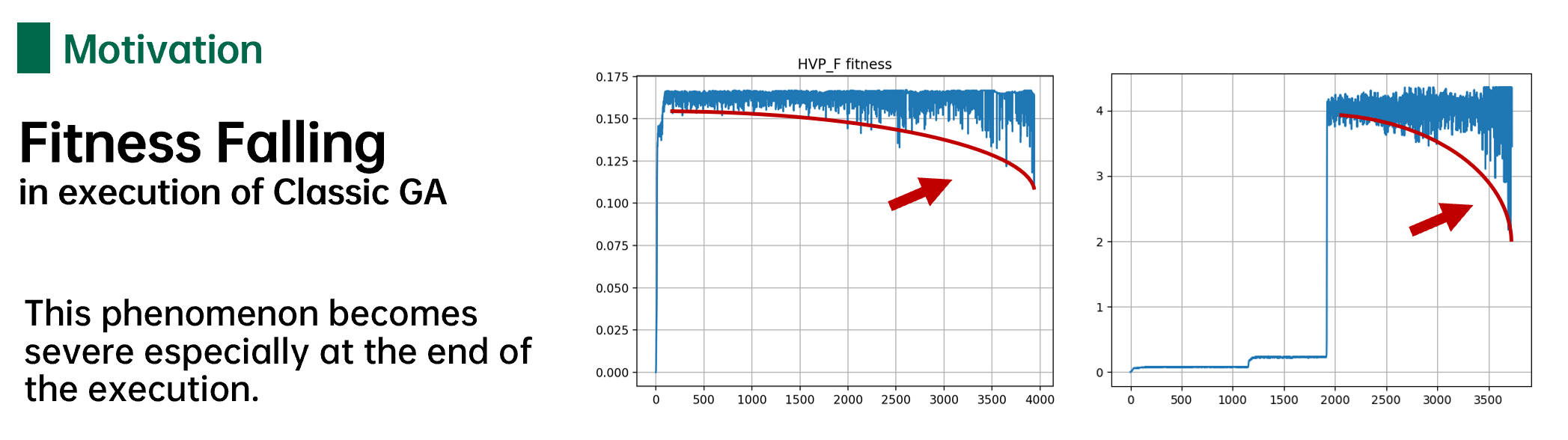
导致适应度下降的原因分析如下，随着进化的不断深入，在进化接近全局最优解时，种群中的优秀个体数量以指数型增长，最终整个种群中的几乎所有个体都具有较高的适应度。然而经典遗传算法中的是突变概率\(p_m\)固定的，在进化接近全局最优解时，突变对整个种群个体的破坏能力达到最大。
基于上述分析，如果可以自适应的根据进化过程调整突变和交叉的概率，使得可以在进化接近最优解时降低突变和交叉的概率，那么这种适应度下降的现象将被消除。

理论

自适应遗传算法(Adaptive Genetic Algorithm, AGA)就是这样一种能够根据个体的表现来自动调整突变和交叉概率的遗传算法。在自适应遗传算法中，每个个体所拥有的交叉和突变的概率如下：
\[p_c=\begin{cases} k_1\frac{f_{max}-f'}{f_{max}-\overline{f}},f'≥\overline{f} \\ k_3, f'<\overline{f} \end{cases}\]

其中\(f'\)表示一个配对中的两个个体中具有较大适应度的那个个体的适应度；\(f_{max}\)为现有种群中最大个体的适应度；\(\overline{f}\)是现有种群的平均适应度；\(k_1\)和\(k_3\)是常数。

\[p_m=\begin{cases} k_2\frac{f_{max}-f}{f_{max}-\overline{f}},f≥\overline{f} \\ k_4, f<\overline{f} \end{cases}\]

其中\(k_2\)和\(k_4\)都是常数。

讨论

以个体的突变概率为例，当个体的适应度处于平均水平，即\(f=\overline{f}\)时，其突变概率为：
\[p_m=k_2\]

当个体的适应度高于当前种群的平均表现，即\(f>\overline{f}\)时，其突变概率与个体适应度有关：个体适应度越高，其突变概率越小，最小的突变概率为：
\[min(p_m)=\lim_{f→f_{max}}k_2\frac{f_{max}-f}{f_max-\overline{f}}=0\]

当个体的适应度低于当前种群的平均表现，即\(f<\overline{f}\)时，其突变概率为：
\[p_m=k_4\]

通过如上的讨论，可以说明自适应遗传算法可以控制突变所带来的消极效应。同时\(k_2\)和\(k_4\)应当设置的相对比较大，如此使得所有低于和等于个体平均水平的个体都可以被完全打乱重新寻找。

Python实现

选择

接经典遗传算法的Python实现一章，由于交叉和突变都需要根据每个个体的适应度，因此需要对原本的选择函数做出调整，使之能输出被选择的每个个体的适应度，保存在一个列表中。

1
fitness_inter.append(fitness[i]) # copy the fitness
完整代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def adaptive_selection(population: 'list', fitness:'list', avg_fitness=None) -> ['list','list','int']:
    '''
    Function:
    produce the indiv to the intermediate population based on its fitness.

    Parameters:
    population - two dimension list
    fitness - list, the unnomalized fitenss
    avg_fitness - optional float, the average fitness of the current population

    Return:
    population_inter - two dimension list
    individual_number - int, number of unique indiv. in each population
    '''
    population_inter = [[]]
    fitness_inter = []
    if avg_fitness == None:
        avg_fitness = sum(fitness) / float(len(fitness)) # calculate the average fitness

    print('selection')

    for i in range(len(population)):
        # based on the integer part of the fitness, copy to the intermediate population
        copy_times = 0
        fitness_norm_i = fitness[i] / avg_fitness # normalize the fitness
        for j in range(int(fitness_norm_i)):
            population_inter.append(population[i])
            fitness_inter.append(fitness[i]) # same operation to the fitness
            copy_times = copy_times + 1
            print('indiv:*', i, '   normal fitness:', fitness_norm_i,
                  '   Copy times:', copy_times)
        # based on the fraction part of the fitness, extra chance of production
        if random.random() < (fitness_norm_i - int(fitness_norm_i)):
            population_inter.append(population[i])
            fitness_inter.append(fitness[i]) # same operation to the fitness
            copy_times = copy_times + 1
            print('indiv:*', i, '   normal fitness:', fitness_norm_i,
                  '   Copy times:', copy_times, '   extra')
        else:
            print('indiv:*', i, '   normal fitness:', fitness_norm_i,
                  '   No extra copy')
        # number of unique indiv. in each population
        individual_number = len(list(set([tuple(t) for t in population_inter[1:]])))
    return population_inter[1:], fitness_inter, individual_number

自适应单点交叉

现在的单点交叉需要根据个体的适应度进行。单点交叉的第一步仍然是随机配对，但是此处也需要对传入的中间种的适应度列表做同样的随机配对以匹配个体：

1
2
3
4
5
6
randnum = random.randint(0, 100)
random.seed(randnum)
random.shuffle(fitness)
random.seed(randnum)
random.shuffle(population)
print('shuffle')
然后对于每一个配对，比较配对中两个个体的适应度以确定\(f'\)：
1
2
3
4
5
6
for i in range(0, population_size - 1, 2):
    # determine the larger fitness in a pair
    if fitness[i] > fitness[i + 1]:
        larger_fitness_inpair = fitness[i]
    else:
        larger_fitness_inpair = fitness[i + 1]

用选择结构实现自适应概率的设置：

1
2
3
4
5
6
7
if larger_fitness_inpair < avg_fitness:
    pc = k3
    print('low pair, crossover rate:', pc)
else:
    pc = k1 * (max_fitness -
            larger_fitness_inpair) / (max_fitness - avg_fitness)+adjust
    print('high pair, crossover rate:', pc)

完整代码如下：
(对于adjustment参数的添加请见下一节)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
def adaptive_single_crossover(population: 'list',
                              fitness: 'list',
                              max_fitness: 'float',
                              avg_fitness: 'float',
                              k1=0.9,
                              k3=0.9,
                              adjust=0) -> ['list', 'bool']:
    '''
    Function:
    do the adaptive single crossover based on fitness.

    Parameters:
    population - two dimension list
    fitness - list, fitness list of intermediate population
    max_fitness - float, the max fitness in the current population
    avg_fitness - float, the average fitness in the current population
    k1 - 0 <=float<= 1, the max crossover rate when f' >= avg_fmax_fitness_inpair
    k3 - 0 <=float<= 1, the fixed crossover rate when f' < avg_f
    adjust - 0<=float<=1, the compensated probability of crossover

    Return:
    population - two dimension list
    True or False - bool value
                    if there is only one indiv in current population, the function will return False
                    otherwise, it will return True
    '''
    population_size = len(population)
    pc = 0
    # check whether there is only one indiv in the population
    if population_size == 1:
        print('【Warning】only one indiv in current population')
        return population, False
    # check whether k1>1
    elif k1 > 1 or k1 < 0:
        print('【Warning】k1>1')
        return population, False
    # check whether k3>1
    elif k3 > 1 or k3 < 0:
        print('【Warning】k3>1')
        return population, False
    else:
        print('adaptive single crossover')
        # random shuffle the fitness and population with the same seed
        randnum = random.randint(0, 100)
        random.seed(randnum)
        random.shuffle(fitness)
        random.seed(randnum)
        random.shuffle(population)
        print('shuffle')

        for i in range(0, population_size - 1, 2):
            # determine the larger fitness in a pair
            if fitness[i] > fitness[i + 1]:
                larger_fitness_inpair = fitness[i]
            else:
                larger_fitness_inpair = fitness[i + 1]

            if larger_fitness_inpair < avg_fitness:
                pc = k3
                print('low pair, crossover rate:', pc)
            else:
                pc = k1 * (max_fitness -
                           larger_fitness_inpair) / (max_fitness - avg_fitness)+adjust
                print('high pair, crossover rate:', pc)

            print('==== crossover rate:', pc, '====')

            # check each indiv with adaptive crossover rate
            if random.random() < pc:
                print('indiv:', i, '   chromosome:', population[i],
                      '   crossovered: yes')
                print('indiv:', i + 1, '   chromosome:', population[i + 1],
                      '   crossovered: yes')
                population[i], population[i + 1] = crossover(
                    population[i], population[i + 1])
                print('---after crossover---')
                print('indiv:', i, '   chromosome:', population[i],
                      '   crossovered: yes')
                print('indiv:', i + 1, '   chromosome:', population[i + 1],
                      '   crossovered: yes')
            else:
                # keep origin
                print('indiv:', i, '   chromosome:', population[i],
                      '   crossovered: not')
                print('indiv:', i + 1, '   chromosome:', population[i + 1],
                      '   crossovered: not')
        return population, True

自适应突变

相比于经典遗传算法，依照理论，自适应遗传算法中的突变概率与个体适应度的相关：

1
2
3
4
5
for i in range(population_size):
    if fitness[i] < avg_fitness:
        pm = k4
    else:
        pm = k2 * (max_fitness - fitness[i]) / (max_fitness - avg_fitness)+adjust

完整代码如下：
(对于adjustment参数的添加请见下一节)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def adaptive_mutation(population: 'list',
                      fitness: 'list',
                      max_fitness: 'float',
                      avg_fitness: 'float',
                      k2=0.05,
                      k4=0.05,
                      adjust=0) -> 'list':
    '''
    Function:
    do the mutation based on the mutation rate.

    Parameters:
    population - two dimension list
    fitness - list, the fitness list of intermediate populaton
    k2 - 0 <=float<= 1, the max mutation rate when f' >= avg_fmax_fitness_inpair
    k4 - 0 <=float<= 1, the fixed mutation rate when f' < avg_f
    adjust - 0<=float<=1, the compensated probability of mutation
    Return:
    population - two dimension list
    '''
    population_size = len(population)
    chromesome_length = len(population[0])
    pm = 0
    print('adaptive mutation')

    for i in range(population_size):
        if fitness[i] < avg_fitness:
            pm = k4
        else:
            pm = k2 * (max_fitness - fitness[i]) / (max_fitness - avg_fitness)+adjust
        # chech each indiv with mutation rate
        if random.random() < pm:
            mutation_point = random.randint(
                0, chromesome_length - 1)  # random select the mutation point
            print('indiv:', i, '   chromosome:', population[i],
                  '   mutated: yes', '   mutation point:', mutation_point,
                  '   muation rate:', pm)
            population[i][mutation_point] = bit_inverse(population[i][mutation_point])
            print('---after mutation---')
            print('indiv:', i, '   chromosome:', population[i],
                  '   mutated: yes', '   mutation point:', mutation_point,
                  '   muation rate:', pm)
        else:
            print('indiv:', i, '   chromosome:', population[i],
                  '   mutated: not', '   muation rate:', pm)
        print('========')
    return population

结果和改进

结果

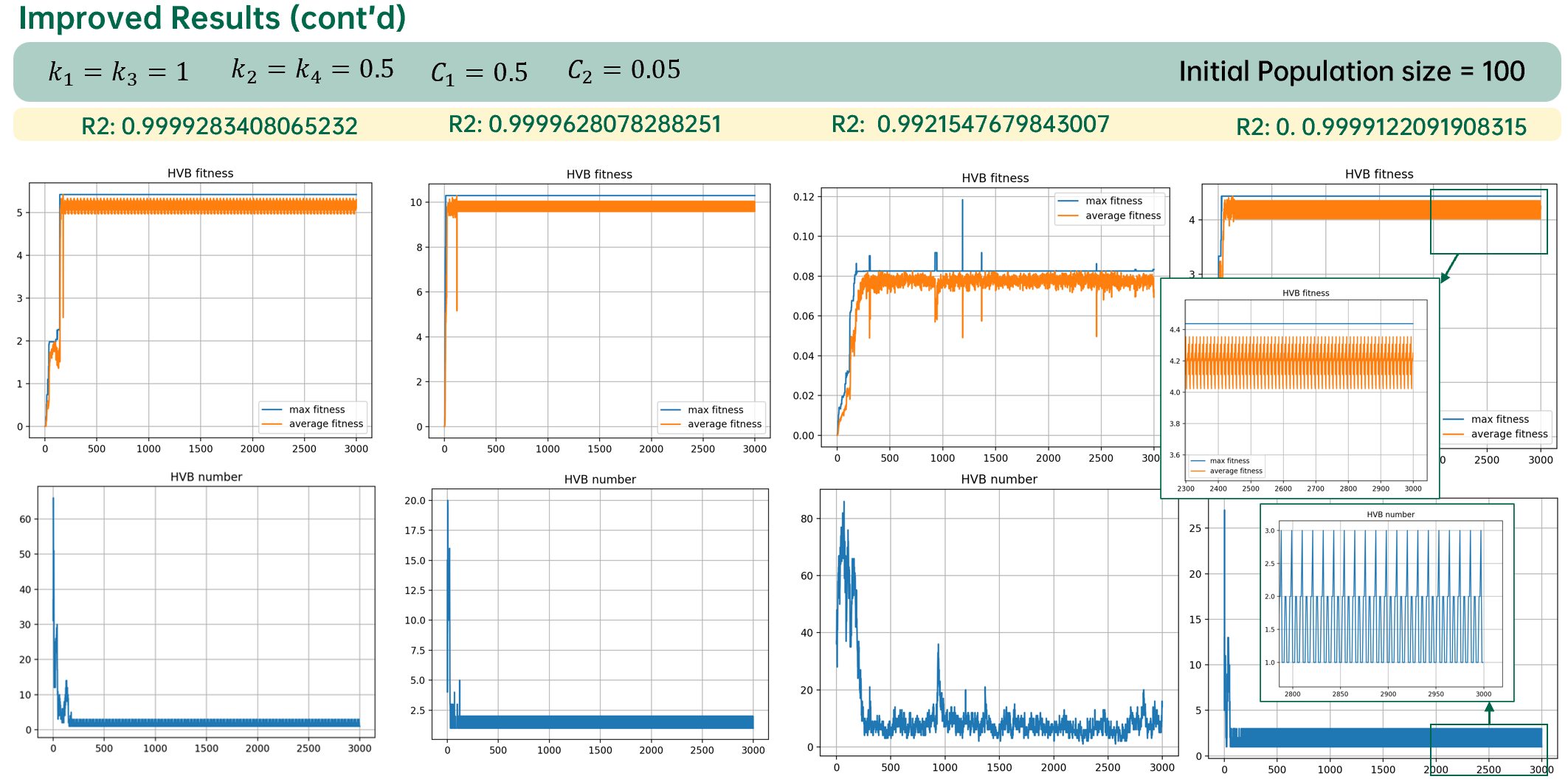
使用自适应遗传算法挖掘线性公式系数的结果如下图所示：

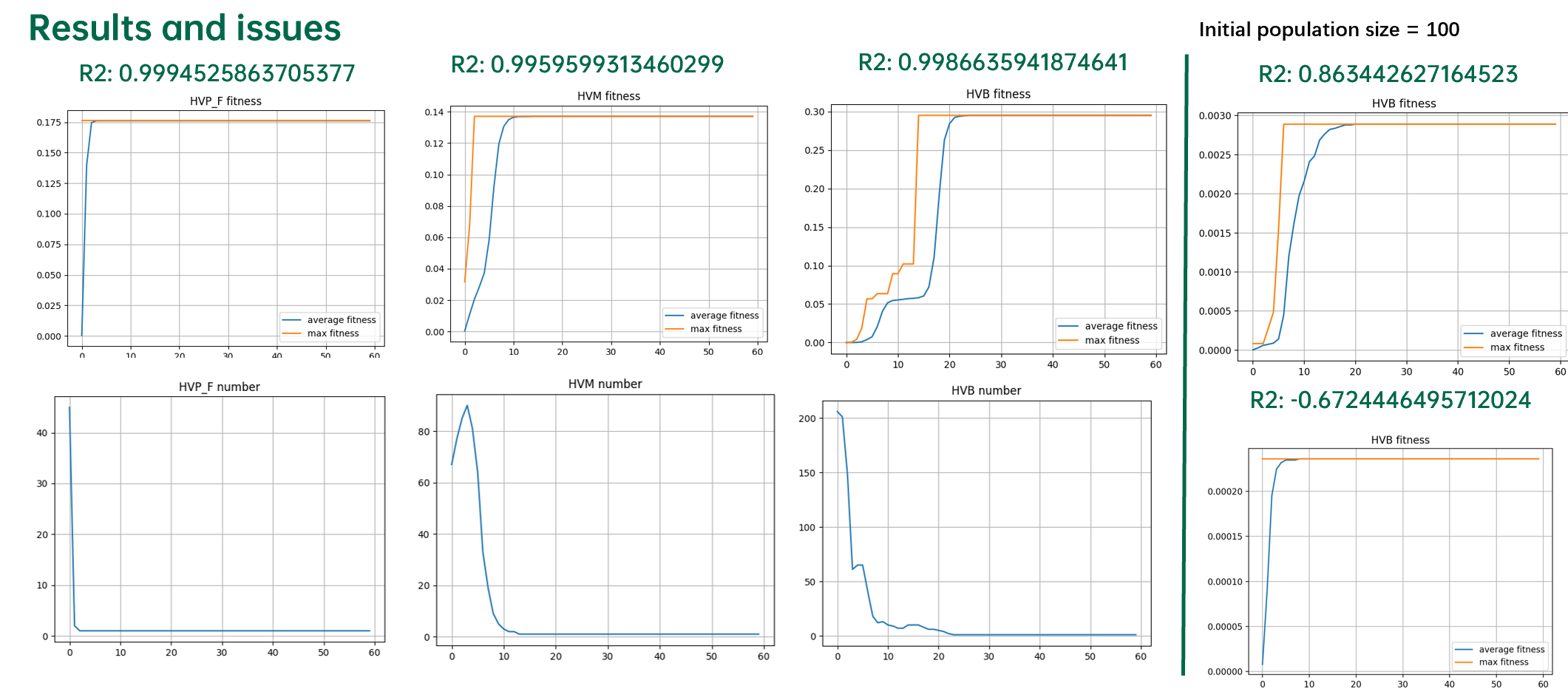
从上图可以看出，适应度下降的现象被完全消除。但是算法极其容易陷入局部最优值。
从结果上可以发现，自适应遗传算法由于对于当前种群中适应度最大的个体的突变概率为0，因此在抹除突变的消极效应的同时也抹除了积极效应。
\[min(p_m)=\lim_{f→f_{max}}k_2\frac{f_{max}-f}{f_max-\overline{f}}=0\]

改进

一种可行方法是在交叉和突变的概率下增加两个常数\(C_1\)、\(C_2\)：
\[p_c=\begin{cases} k_1\frac{f_{max}-f'}{f_{max}-\overline{f}}+C_1,f'≥\overline{f} \\ k_3, f'<\overline{f} \end{cases}\]

\[p_m=\begin{cases} k_2\frac{f_{max}-f}{f_{max}-\overline{f}}+C_2,f≥\overline{f} \\ k_4, f<\overline{f} \end{cases}\]

使得：
\[min(p_m)=\lim_{f→f_{max}}k_2\frac{f_{max}-f}{f_max-\overline{f}}+C_2=C_2\]

如此最小概率将不是零，保留了突变的积极效应，同时自适应调整可以保证收敛的稳定，一定程度上降低了突变的消极效应。
下图是使用自适应遗传算法优化的结果：

论文 > 进化计算 > 遗传算法
自适应遗传算法的Python实现
https://l61012345.top/2023/01/21/论文/进化计算/遗传算法/自适应遗传算法的Python实现/
作者
Oreki Kigiha
发布于
2023年1月21日
更新于
2023年12月12日
许可协议