02. 背景·遗传编程基础

背景·遗传编程基础

这是对《Genetic Programming IV: Routine Human-Competitive Machine Intelligence》的笔记，本页对应第二章： Chapter 2： Background on Gentic Programming.
这一章讲述了遗传编程的运行流程，以及遗传编程的高级功能。

原书的免费公开版本在作者Koza本人的Research gate主页上：https://www.researchgate.net/publication/243776894_Genetic_Programming_IV_Routine_Human-Competitive_Machine_Intelligence
这本书也可以在Springer 购买电子版： https://link.springer.com/book/10.1007/b137549
或者在亚马逊英国购买纸质版： https://www.amazon.co.uk/Genetic-Programming-IV-Human-Competitive-Intelligence/dp/0387250670

遗传编程是一种独立于特定领域(domain-independent)的搜索方法，它可以遵循遗传的方式为目标问题产生出一个用于解决这个问题的计算机程序的集合（称为一个种群,population）。具体而言，遗传编程通过模拟自然界中进化的方式来更新种群。

遗传编程的准备工作

这一节的内容基本上同上一章的1.1.6小节。

遗传编程准备工作的实质是人类使用者将对问题的描述和期望所达成的目标进行高等级的描述，使计算机可以理解，并且辅佐以控制参数来控制遗传编程程序的运行和终值。
在运行之前人类使用者需要做的准备工作一共有五个：

1. 确定基函数集合
2. 确定端点集合
3. 确定衡量适应度的方式
4. 确定控制运行过程的控制方式
5. 确定何时停止算法运行，并规定如何确定最终的解。

前两条是用于描述整个问题，基函数集合和端点集合被用于确定计算机程序的基本“原材料”。对于一些问题，函数集中可能存在加减乘除之类的数学运算符和条件分支运算符(conditional branching operator)（比如IF-THEN）结构。而端点集中可能存在外部的独立输入变量和常数。

遗传编程的函数集中允许存在循环结构吗？

• 事实上这个问题在《GP IV》这本书中的描述非常的模糊。因为在此处第一次正式出现函数集结构时作者只提到了存在条件分支结构，并未提到循环结构的参与。但是在随后第40页2.3.3一节中出现了自动定义循环，也就是作者认为遗传编程中是可以实现循环结构的。
  但是如果我们细致的分析，LISP语言中存在两种循环结构，一种是进行判断退出的loop函数、另一种是进行进行进入判断的dotimes结构。遗传编程应该只能实现判断退出的loop函数，即生成树的函数集合中添加loop和条件退出(when ()(return )，甚至return结构都不应该被使用)两种结构，如此使得树可以生成条件退出的循环，但是循环内部的大小可能非常大，而且不容易控制。如果是条件进入的循环，整个树形结构将会崩毁。

第三条的本质上是对问题解决方案的期望的高级描述。
第四条和第五条是为了控制遗传编程的运行过程。其中最重要的控制参数是种群大小，在这本书中，作者通常根据“在容忍的计算时间内可以产生最大的代数”来设置种群的大小。终止条件通常是最大代数或者是达到预期结果的表征。本书当中所有的程序的终止条件都是连续多轮种群中的最大适应度在期望的范围内。
由于最终的结果应该是一个含有若干个个体的种群，因此还需要确定选择哪一个个体作为最终的解。（*单目标问题中）通常选择最后一代中适应度最高的个体。

多目标问题中最终解的选取规则有非常多，但是基本上还是依照使用者对不同目标的偏好进行选择。

遗传编程的运行

遗传编程的运行从随机初始化个体形成初始种群开始，个体通过适应度函数对其量化评估，得到个体的适应度后，基于适应度，有概率地挑选个体进行遗传操作，生成下一代种群。整个运行的流程图如下所示。

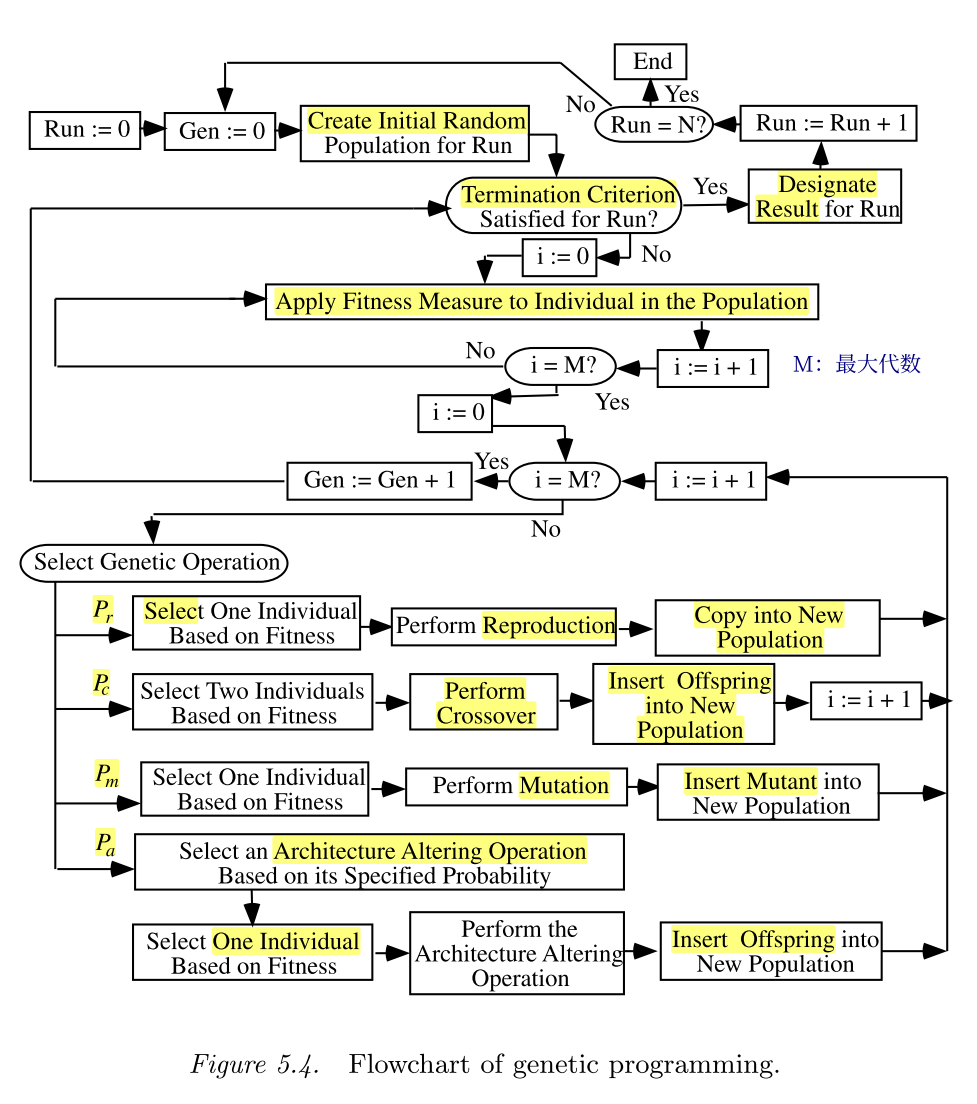
总的运行流程可以描述为：

1. 随机生成初始种群，它们是树形结构的，从可用的基函数集和端点集中挑选出来生成。
   

   树的生成方式有Full和Grow两种，具体在遗传编程导论中。

   
   

   这里是书中第一次强调遗传编程中的个体是树形结构的，遗传编程中使用树形结构的原因是因为LISP语言使用的S表达是树形结构的。

2. 迭代更新种群的过程有可以分为如下子步骤，这个循环会运行到满足设定的终止条件为止：

   1. 编译运行每一个个体对应的程序，然后使用之前定义的适应度评估方法对个体的适应度进行评估。
      
   2. 根据个体的适应度，有概率地选择一个或者两个个体进行如下的操作：

      • 繁殖 (reproduction)
        根据个体的适应度，直接将这个个体复制到下一代的种群中。
        

      • 交叉 (crossover)
        

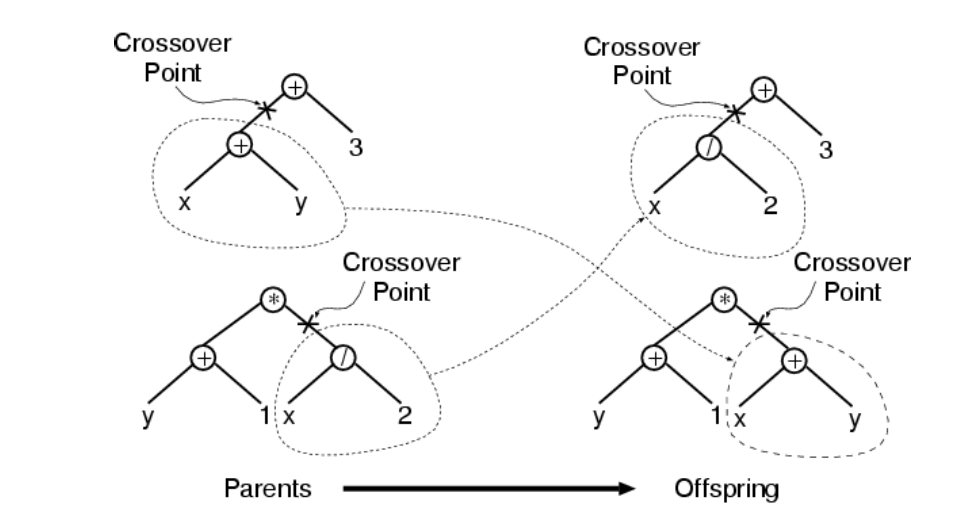
        交叉的步骤是：
        基于概率\(p_c\)和适应度从当前种群中选择两个个体，随机的选择两个个体某一位置上的一个连接或者结点作为交叉点，然后交换两个体交叉点以下的子树。
        通常选择函数作为交叉点的概率要远高于端点作为交叉点的概率（比如90%的概率选择一个函数，10%的概率选择端点。），这是因为选择函数作为交叉点时，交叉对个体的影响更大，遗传编程在搜索空间中单次搜索的范围更广。

      • 突变 (mutation)
        

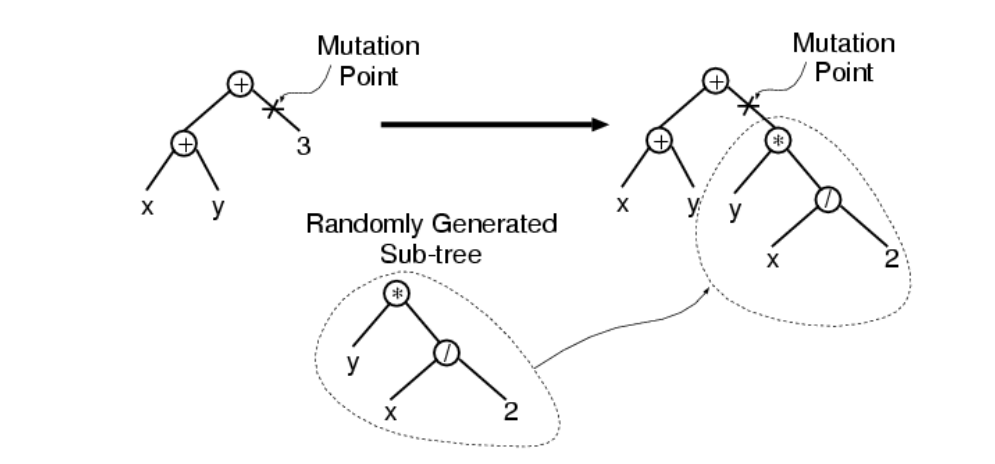
        突变的步骤是：
        基于概率\(p_m\)和适应度从当前种群中选择一个个体，并随机在这个个体内选择一个突变点，突变点下的子树被一个随机生成的子树替代（相当于与这个随机生成的子树发生交叉）。
        

      • 结构变换操作 (architecture-altering operation)
        结构转换会在之后的节中详述，在此不做叙述。

需要注意的是，和遗传算法不同的是，遗传编程中不存在中间种(intermediate population)这个概念，四次对当前种群的选择均是独立进行的。遗传算法中是先创建中间种，然后从中间种中选择个体进行串行的遗传操作。相对比，此处遗传操作是并行进行的，并且每个遗传操作是直接从当前种群中选择的个体。
这样导致的结果是：
遗传编程中并行的操作不会积累遗传物质和遗传效应。而串行的操作是会积累的。遗传编程中四次选择的目标种群中不存在多个相同的个体，也就不存在对同一个个体的若干进化可能分支。这样细小的差别在个体数量非常庞大时对进化的影响会被体现出来。

遗传编程的并行化执行和所使用的LISP语言的限制有关。

遗传编程基于个体的适应度，有概率的对个体进行这些遗传操作。通常个体的适应度越高，个体被选中进行遗传操作的概率就更高，这暗示了遗传编程将更倾向于在高适应度个体的周围去搜索搜索空间中的其他个体。通常选择个体进行遗传操作的算法有轮盘赌算法和锦标赛算法，这些算法都不是贪心算法，即是从全局而非当前的局部最优来考虑优化问题。这种非贪心的特性能够保证遗传编程/遗传算法不会陷入局部最优解。

但是在一些文献中仍然声称GEP和GP是会陷入局部最优解的，GP和GEP陷入局部最优解的原因是所使用的树的深度并未能达到足够表达全局最优解的精度。在树的深度足够的情况下，GP和GEP是可以找到全局最优解的。

遗传编程的运行案例

这一节将举例说明遗传编程是如何通过遗传操作解决目标问题的。目标问题为自动的生成一个程序使得其在\(x ∈ [-1,1]\)区间内生成的值满足函数\(x^2+x+1\)。这种试图发现某种隐藏的数学公式，以此利用特征变量预测目标变量的问题称之为符号回归（symbolic regression）类问题。

搜索空间确定和参数设置

对于这个问题，在遗传编程的准备阶段，端点集由随机常数和变量\(x\)构成：
\[T=\{X,ℜ\}\] 其中的\(ℜ\)表示一个随机数，人为地设置其范围为\(ℜ∈[-5.0,5.0]\)。
接下来指定遗传编程的函数集，可以将函数集设置为四则运算即可：
\[F=\{+,-,×,\%\}\]

为了避免运行错误，指定了\(ℜ÷0=1\)。

初始种群中的每一个个体都将从端点集和函数集中生成。生成之后的个体需要用适应度函数对其评估，在这个问题中，适应度函数可以通过当前个体\(\hat{y}\)与目标函数\(y_e=x^2+x+1\)在\(x ∈ [-1,1]\)上的值的差距来衡量。定义这个问题中的适应度函数为：
\[f(i)=∫_{-1}^1|\hat{y_i}-y_e|dx\] 对于这个适应度函数而言，个体的适应度越小代表与目标函数的差距越小，个体表现更加“优秀”。 接下来应当决定运行参数，为了简化解释，此处设定每一代中仅存在四个个体（但是实际上每一代的个体数量往往是成千或者百万级别的）并设置各遗传操作发生的概率，通常情况下设置交叉的概率为90%，繁殖的概率为8%，突变的概率为1%，结构变换的概率为1%。

GP通过交叉对搜索空间进行查找，因此交叉的概率应当比较大，才能保证搜索空间中的个体尽可能被搜索完全。
由于本书的作者所强调的“遗传多样性”，因此直接对个体的复制应当保留在一个非常低的概率，以产生更多可能的个体结构。
突变和结构变换的随机性会带来负面效应，因此应当尽量保持在非常低的水平。事实上突变和结构变换对于遗传编程中的个体的打击几乎是毁灭性的。

最后设置运行的终止条件，对于回归问题通常可以设置个体与目标之间的差值低于某一水平时终止运行。在这个例子中设定当出现适应度小于0.01的个体时，遗传编程终止运行。

初始种群生成和个体评估

初始种群从搜索空间中随机挑选得到，这个例子中随机生成的初始种群中的四个个体如下图所示：

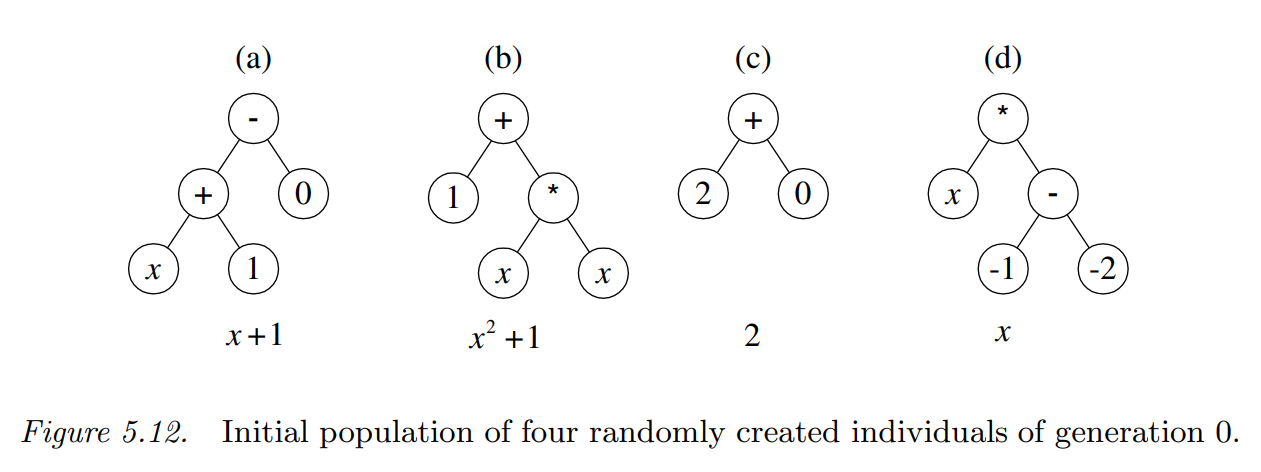
通过解释，这四个个体表示为：\(x+1\)、\(x^2+1\)、\(2\)和\(x\)。
将这四个个体\(\hat{y}\)分别带入适应度函数中，可以计算得出四个个体的适应度为0.67、1.0、1.67和2.67，可视化表示如下图所示：

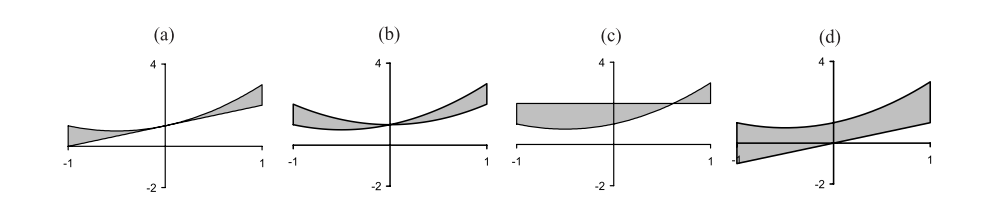
可以发现前两个个体(a)、(b)的适应度更低（或者说更“好”），在这个例子中意味着这两个个体更接近与目标，它们有更高的概率被选择做遗传操作。

遗传操作

复制

由于个体(a)适应度最好，它更有高概率被选择。此处假设它被选择出来进行复制操作，它被复制到下一代种群中。即它在下一代被保留。

突变

假设个体(c)的某个点位发生了突变，其下面的子树会被一个随机生成的子树替代，如图所示。

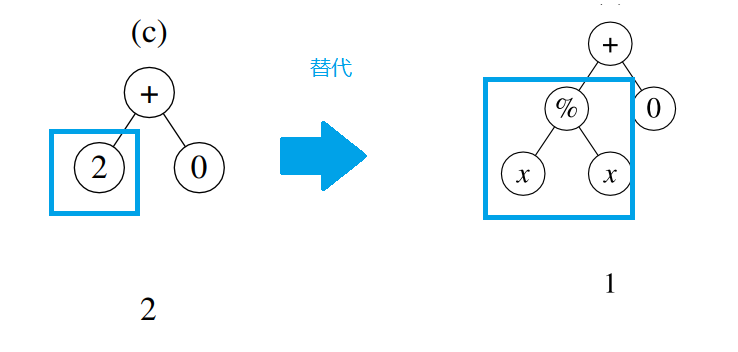
可以发现，原本适应度不佳的个体(c)通过突变后，其适应度可能会有所好转。除了在运行快要收敛时对现有种群施加扰动、改善算法的运行情况外，突变还能够有概率地改善适应度不加的个体的适应度，在搜索空间中调整在这些点附近的查找方向。

交叉

前两个个体(a)、(b)的适应度更好，更有高概率被选择配对进行交叉操作，假设(a)(b)个体发生如下图所示的交叉：

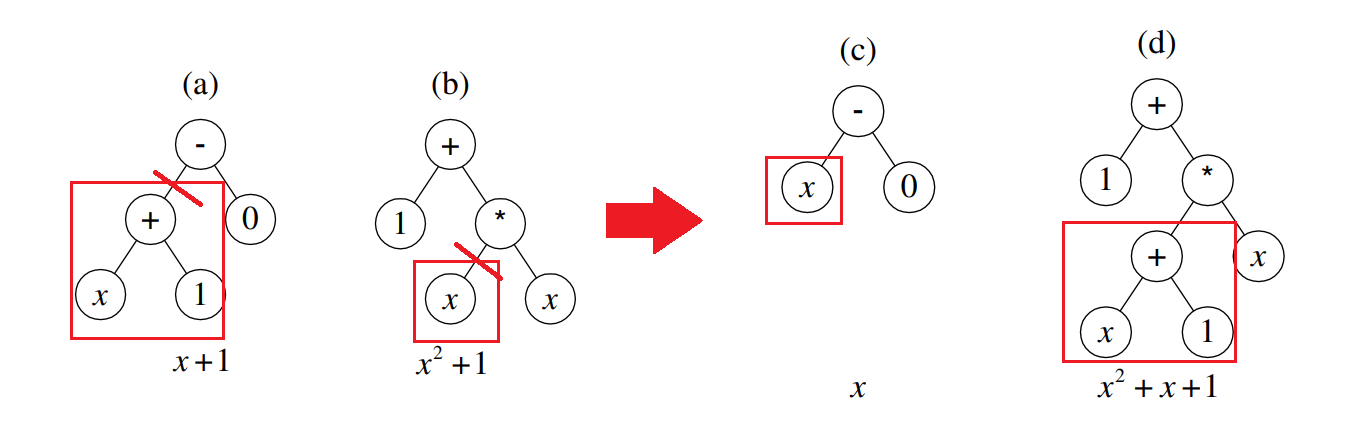
可以发现，个体(a)和个体(b)中各自都有一部分贴近于目标函数（称为各自的优良性状），通过交叉，两个亲本的优良性状更容易被结合，从而生成更加贴近目标的后代。

终止

通过遗传操作后的后代如下图所示：

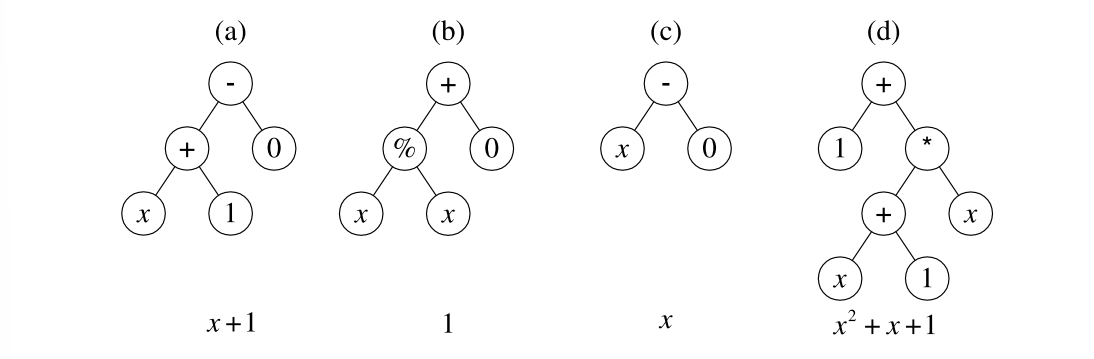
可以发现，个体(d)的适应度已经为0，达到了预先设定的终止条件，遗传编程停止运行。

遗传编程的高级功能

以我自己的观点来说，这些高级功能被设计出来的目的是为了弥补遗传编程自身存在的缺陷，比如强类型用于解决遗传操作不合法的问题、自动定义函数用于解决遗传操作对有效基因破坏力度大的问题、结构变换操作用于解决“基因多样性”的问题。这些机制相当于补丁，但是引入之后又会为遗传编程带来更大的问题。
以我自己的观点来说，这些高级功能被设计出来的目的是为了弥补遗传编程自身存在的缺陷，比如强类型用于解决遗传操作不合法的问题、自动定义函数用于解决遗传操作对有效基因破坏力度大的问题、结构变换操作用于解决“基因多样性”的问题（尤其是在引入类保护的变异之后个体的结构基本上从生成开始就不会改变了）。这些机制相当于补丁，但是引入之后又会为遗传编程带来更大的问题。

强类型

对许多问题而言，函数集和端点集都需要是强类型的(constrained syntactic structures)，也就是说，一个函数下侧连接的子树和端点的类型是需要被指定的。遗传编程实现强类型的方式是使用若干个函数集和端点集来满足不同函数的语法需求。

以我的观点，强类型的本质是利用先验知识在搜索空间中强行规避一些不合法的部分被搜索到。
以我的观点，强类型的函数集和端点集必须是整个遗传编程使用的函数集和端点集的对应子集，否则搜索空间会出现扭曲和不规则的扩张。

自动定义函数

自动定义函数是利用问题对称性、规律性和模块化的特点，将目标问题分解为若干个子问题，并对子问题进行分别解答后进行合并。这些子问题的解答就是自动定义函数(automatically defined functions, ADF). 自动定义函数与个体一同进化，但是相对独立，具体的介绍在：
遗传编程中的自动定义函数

有自动定义函数之后，和自动定义函数的机制类似，也有自动定义循环、自动定义递归等等。

程序结构和结构变换操作

程序的结构需要由用户首先指定，但是通过结构变换操作(architecture-altering operation,AAO)可以进化改进程序的结构。
具体的介绍在结构变换操作

遗传编程问题解决器

遗传编程可用于为无数不同领域的问题提供解决方案。无论在哪个领域实施，遗传编程几乎总是遵循相同的严格但基本的框架。因此，如果能以简单明了的方式提供基本的遗传编程框架，就能很好地为程序员服务，使他们可以相对轻松地解决这一范例中的问题。
现有系统旨在为程序员提供用遗传编程解决一般问题的框架，但一般都过于复杂，难以操作。现有的两个这样的系统是 gpc++ 及其 Java 移植版本 gpj++。这些系统要求程序员将基因编程系统的一般要求与其自身的严格框架相匹配。例如，它们假定程序员将以一种非常特定的格式来表示要培育的程序或函数，这样系统就能自己进行基因重组。虽然这也是一种有用的工具，但同样有用的是，将某些实现决定权完全留给程序员，因为这些决定权往往在很大程度上取决于相关领域。

遗传编程问题解决器(Genetic Programming Problem Solver, GPPS)是一种通用的遗传编程框架。这些组件是所有遗传编程程序共有的部分。它们是执行选择、变异、交叉和复制的功能。抽象的其他功能可能包括检查终止条件、测试个体的适应性、打印结果等方法。基于上述考虑，在构建系统时，程序员只需关注其具体问题的实现，而无需关注基因程序在个体空间中的搜索方式。也就是说，在给定一个必须遵循的模板后，程序员只需深入研究其问题的具体细节，就能实现 GP 的基本部分（变异、交叉等）。

上述这段话的来源是：https://www1.cs.columbia.edu/~evs/ais/finalprojs/kalina/

由于GPPS本身自带一个通用的函数集（包括四则运算和条件选择）和一个通用的端点集（包括输入向量和常数），因此用户在使用GPPS时无需指定函数集和端点集。
在GPPS2.0中，用户甚至不需要自己指定子函数、递归和循环结构的优先级。

遗传编程系列书籍的主要观点

遗传编程系列书籍的主要观点如下图所示：

其中需要强调的几个点：

• 92版书中指出，几乎所有的问题都可以视为对计算机程序的搜索。这句话强调了遗传编程解决问题的潜能。
  
• 94版书中的论点基本上都和自动定义函数有关。