基于互信息的语义模式定理和遗传编程

背景

遗传算法中的模式定理

所谓模式(schema)是指在搜索空间中一组具有某些共同特征的点的集合。模式的定义最早在遗传算法领域由Holland提出，他认为遗传算法中的模式是带有Don't care (*)的位串(string)，Don't care部分的比特既可以是0也可以是1，因此一个模式实际上代表了若干种不同的个体。进一步地，Holland提出了模式定理(schema theory)，这个定理给出了某个特定的模式群体\(H\)在下一代\(t+1\)中被采样概率的下限，也就是这个子种群中的个体存活到下一代后的概率，这个概率表示为：
\[P(H,t+1)≥P(H,t)\frac{f(H,t)}{\overline{f}}\left[1-p_c\frac{Δ(H)}{L-1}\left(1-P(H,t)\frac{f(H,t)}{\overline{f}}\right)\right](1-p_m)^{o(H)}\] 其中\(p_c\)和\(p_m\)分别是交叉和突变的概率；\(Δ(H)\)为\(H\)的定义距；\(o(H)\)为模式\(H\)中有意义的比特数量，称为阶数;\(L\)为个体位串长度；\(f(H,t)\)为第\(t\)代中模式\(H\)的平均适应度，\(\overline{f}\)是第\(t\)代所有个体的平均适应度。
关于遗传算法中的模式定理此处并不展开讨论。
需要知道的是，Holland的模式定理考虑了交叉和突变操作对于模式中有意义部分(也就是非Don't care部分)的结构上的破坏效应(disruptive effect)。
根据Holland的模式理论，定义距小、平均适应度高、阶数更低的模式更容易在进化中被保留和存活，Goldberg将这样的模式称为积木块(Building block)。
在后续的研究中，大部分的研究人员都同意，遗传算法等等一系列的进化计算算法是通过在进化的过程中让个体逐渐积累其承载的building block的个数来让个体的结构逐渐靠近目标解的结构，从而找到全局最优解。

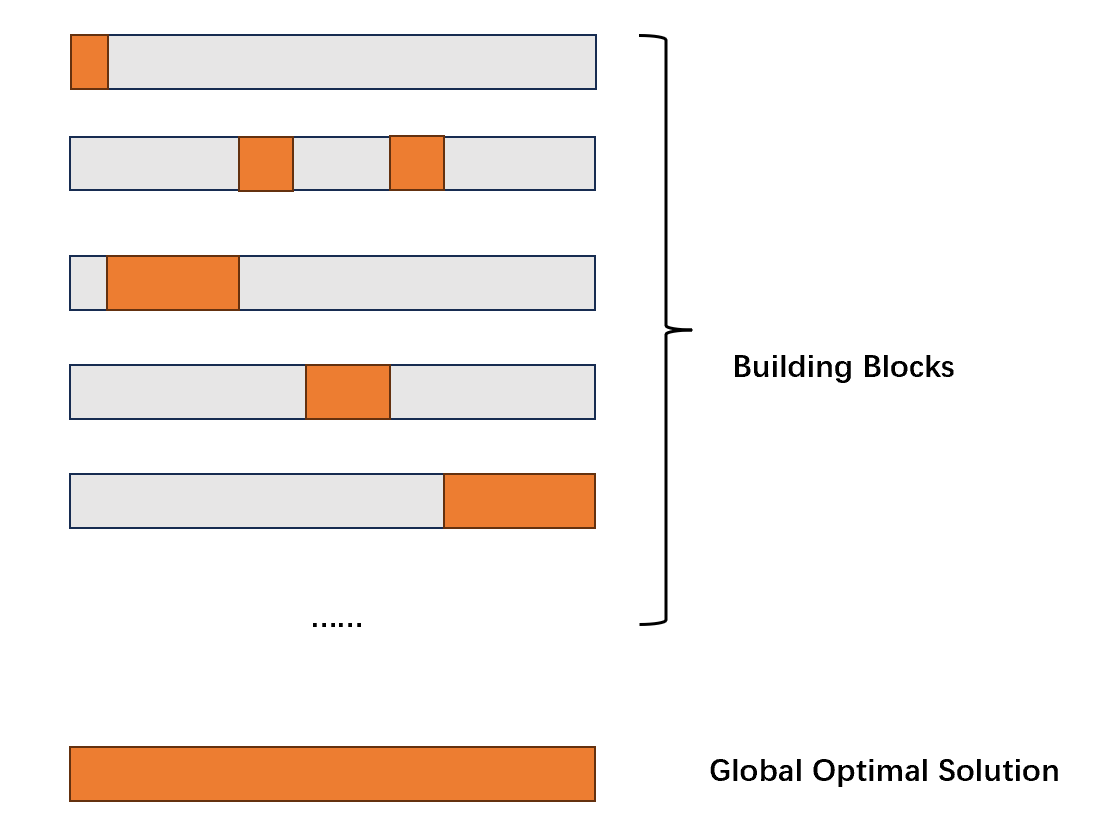
在后面的介绍中，由于习惯，Schema和Building block将不做翻译。

遗传编程中的结构模式及其缺陷

遗传编程中模式定义的发展

遗传编程中对于Schema最为广泛的定义仍然借用了遗传算法中对于模式的定义思路：遗传编程中的模式是搜索空间中一组结构(syntax)特征相似的点的集合。(a set of points in the search space that share some syntactic characteristics.)
类比于遗传算法中带有Don't care的位串，遗传编程中的schema也是一组带有Don't care的树形结构。
最早Altenberg定义遗传编程中的schema为一组含有同一个子树的树形个体，并且给出了在相当多条件限定下的遗传编程的模式定理。之后O'Reilly和Oppacher将Don't care的概念引入了遗传编程的schema，将schema定义为一个含有泛化子树(即用Don't care 作为代替子树，用“#”表示)，Don't care可以表示此处任何有效的子树。每个schema包括两个部分，子树的结构以及相应的最低出现在schema采样(也就是这个schema对应的一群个体)中的出现次数。在之后Poli和Langdon将Don't care的定义延展到了函数集和端点集，并用“=”表示：Don't care可以是任何有效的端点或者函数；他们定义schema是一颗完整的含有“=”的树。之后Poli将两种不同的Don't care结合，定义出Hyper schema：构成schema的函数集中包括=，端点集中则包括了#和=.
关于遗传编程中schema定义的发展在^[1]中有更详细的介绍。

总而言之，这些对模式的定义都认为，结构是承载遗传信息的关键，如果个体的结构越靠近目标解的结构，那么这个个体的表现就越好。因此，遗传编程中设计了以自动定义函数(automatically defined function, ADF)为代表的结构保护机制。以保护有用的结构片段不受到交叉和突变带来的印象。

结构schema的缺陷

上述对于schema的定义都围绕着Don't care，也就是一组结构相似的个体的集合展开。
但是，遗传编程和遗传算法不同的地方来自，在遗传算法的线性结构中，语义的变化与结构的变化是一一对应的。这是Holland的模式定理有效的条件，即搜索空间均匀，变异操作在任意比特上改变所对应的在适应度函数的空间中对应点搜索步长应当是一致的。

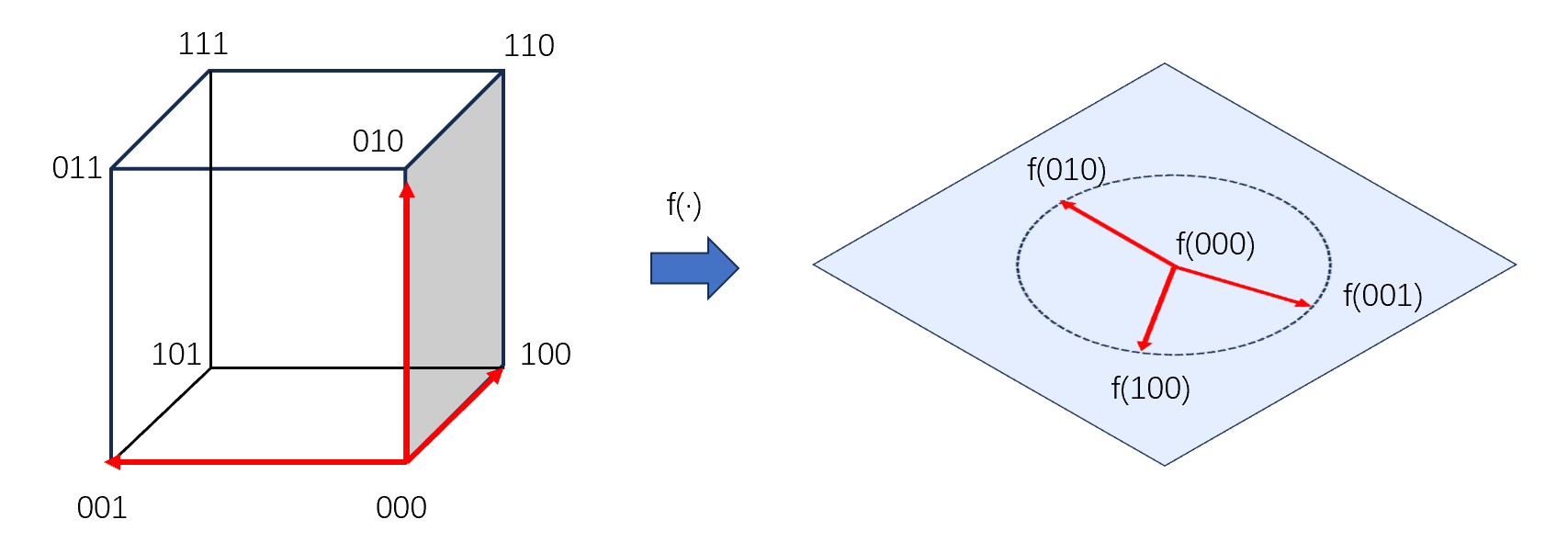
而在遗传编程中，由于函数集的出现导致个体的结构很难做到信息上的的均匀分布，也就是说，位于不同位置上进行的变异操作结果的得到语义可能存在相当巨大的差异。
最终导致的结果是，一个结构的schema，也就是一组结构相似的个体中对应个体的适应度表现差异可能相当巨大。基于结构schema得到的模式定理不能很好的预测某个schema在未来的表现。

基于互信息的语义模式

因此，一部分研究人员认为，相比于归纳个体的结构，更应该归纳个体的表现：将那些表现相似的个体归纳为一个schema，变异和交叉会有大概率在那些表现好的schema中进行，如此可以加快遗传编程的搜索速度。这是基于语义的遗传编程的基本思想。

语义

个体的表现称为语义(semantic)。传统的研究认为，适应度(fitness)可以作为衡量个体语义的标准。但是遗传编程个体结构信息分布的不均匀导致个体或者某些子种群的适应度无法在进化过程中展现连续的变化。此外，适应度对于个体的结构过于敏感以至于无法正确的识别出具有高贡献的building blocks。也就是说具有高贡献的building blocks的个体未必具有高适应度。某些适应度高的个体可能会因为在遗传操作中出现微小的变化而导致适应度急剧下降，反之依然。
因此，除了使用适应度之外，还需要使用别的特征来正确反映种群在进化过程中的进展。

语义在SBGP中的作用整理如下：

• 识别和归纳buidling blocks
  
• 计算当前种群的多样性
• 用于提取聚类中心和计算实例化函数

互信息

^[1]中使用了个体输出与真实输出之间的互信息(mutual information)来衡量个体的语义。一个个体\(t\)的语义具体表示为：
\[S(t)=\frac{I(\hat{Y},Y)}{H(Y)}\] 其中\(Y\)是真实数据集\(\{(x_i,y_i)\}\)中的输出，\(\hat{Y}\)是这棵树在给定数据集的输入时的输出：\(\hat{y}_i=t(x_i)\)；\(I(\hat{Y},Y)\)是两者的互信息，表示为：
\[I(\hat{Y};Y)=\sum_{\hat{y}\in\hat{Y}}\sum_{y\in Y}p(y,\hat{y})log(\frac{p(y,\hat{y})}{p(y)p(\hat{y})})\] 其中\(p(y,\hat{y})\)是\(Y\)和\(\hat{Y}\)的联合概率分布；\(p(y)\)和\(p(\hat{y})\)分别是\(Y\)和\(\hat{Y}\)的边缘概率分布。

\(H(Y)\)是目标输出的信息熵，此处用于进行归一化，表示为：
\[H(Y)=-\sum_{y\in Y}p(y)log(p(y))=I(Y,Y)\]

对两个随机变量\(X\)，\(Y\)，其互信息\(I(X;Y)\)衡量了两者的相互依赖关系，即在一方部分不确定的情况下，另一方的不确定程度。因此\(I(X;X)=H(X)\).其本质上是对联合概率分布定义的拓展，如下图所示：

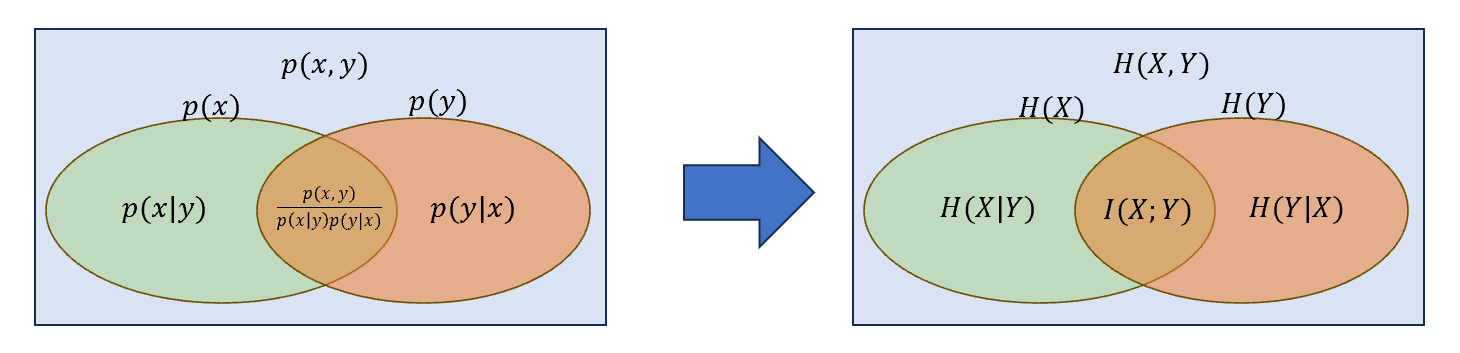
其中\(H(X,Y)\)为\(X\)与\(Y\)的联合熵，有：
\[\begin{aligned} H(X,Y)&=-\sum_{x\in X}\sum_{y \in Y}log(p(x,y))\\ &=H(X|Y)+H(Y|X)+I(X;Y) \end{aligned}\]

在^[2]中作者使用了直方图抽样（即用抽样频率替代总体概率）来估计\(\hat{Y}\)和\(Y\)的互信息，因此上述式子可以改写为：
\[I(\hat{Y};Y)=\sum_{i=1}^{k_{\hat{y}}}\sum_{j=1}^{k_y}\frac{L_{ij}}{N}log\left(\frac{L_{ij}N}{L_iL_j}\right)\] \[H(Y)=-\sum_{j=1}^{k_y}log\left(\frac{L_j}{N}\right)\] 其中\(k_{\hat{y}}\)和\(k_y\)分别是\(\hat{Y}\)和\(Y\)样本统计直方图中的样条(bins)总数；\(N\)是样本数；\(L_i\)是\(\hat{Y}\)的直方图中第\(i\)个样条的纵坐标，代表落入该范围的\(\hat{y}\)的样本的频率；同理\(L_j\)是\(Y\)的直方图中第\(j\)个样条的纵坐标；\(L_{ij}\)代表样本\((\hat{y},y)\)同时落入\(\hat{Y}\)直方图中第\(i\)个样条和\(Y\)直方图中落入第\(j\)个样条的概率。

同时定义，如果两个树\(t_1,t_2\)的输出\(T_1=t_1(X)\),\(T_2=t_2(X)\)存在如下关系：
\[\frac{I(T_1;T_2)}{H(T_1,T_2)}=1\] 称\(t_1\)和\(t_2\)在语义上是相等的。

使用互信息最大的特点是：对随机变量进行平滑可逆的操作（即该映射是一个单射且满射）后，互信息保持不变。
下面折叠的部分对互信息的不变性(invirance)进行了证明^[4]。

互信息不变性的证明

设两个平滑且可逆的函数\(F、G\)有如下关系：\(X=F(U)\)，\(Y=G(V)\)，它们的雅各比行列式表示为：
\[J_X=|\frac{∂X}{∂U}|，J_Y=|\frac{∂Y}{∂V}|\]

雅各比行列式的几何意义和推导

雅各比行列式的定义是：
如果下面等式成立：
\[\begin{cases} y_1=f_1(x_1,...,x_n)\\ y_2=f_2(x_1,...,x_n)\\ ⋮ y_m=f_m(x_1,...,x_n) \end{cases}\] \(f_1,...,f_m\)对\(x_1,...,x_n\)的偏导组成雅各比矩阵：
\[J=\begin{bmatrix} \frac{∂f_1}{∂x_1}&⋯&\frac{∂f_1}{∂x_n}\\ ⋮&⋱&⋮\\ \frac{∂f_m}{∂x_1}&⋯&\frac{∂f_m}{∂x_n}\\ \end{bmatrix}\]

如果\(m=n\)，此时\(J\)为方阵，且\(Y\)对\(X\)为单射且满射，即\(F=\{f_1,...,f_m\}\)可逆，此时雅各比矩阵存在不为零的行列式，即雅各比行列式： \(|J|\).
根据行列式的几何意义：行列式表示的是某个维度的空间中张成空间的面积。

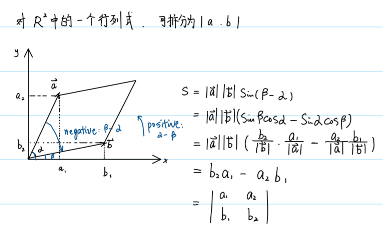
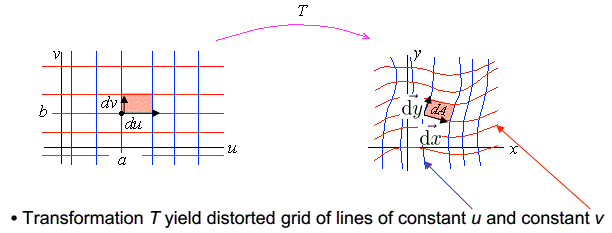
推出，雅各比行列式的意义是维度相同的两个空间：\(Y\)和\(X\)在\(n\)维空间的张成空间的体积比，有：
\[\frac{|Y|}{|X|}=|J|\]

下面给出雅各比行列式在二维空间中的几何意义的证明：
如果有连续且可逆的变换：\(x=x(u,v)\)，\(y=y(u,v)\)，对于\((u,v)\)中一个非常小的矩形，其长宽可以表示为：\(du,dv\)，令：
\[\vec{du}=[du,0],\vec{dv}=[0,dv]\] 那么有：
\[\vec{dx}=\begin{bmatrix}x_u & x_v \\y_u & y_v \\\end{bmatrix}\begin{bmatrix} du \\ 0 \end{bmatrix}\] \[\vec{dy}=\begin{bmatrix}x_u & x_v \\y_u & y_v \\\end{bmatrix}\begin{bmatrix} 0 \\ dv \end{bmatrix}\] 那么在\((x,y)\)空间中的张成空间的面积可以表示为：
\[dA=|\vec{dx}×\vec{dy}|=\begin{bmatrix} x_udu \\ y_udu\end{bmatrix}×\begin{bmatrix} x_vdv \\ y_vdv\end{bmatrix}=(x_uy_v-x_vy_u)dudv=|J|dudv\]

\((u,v)\)空间到\((x,y)\)空间的映射律可以通过对应的雅各比矩阵表示：
\[dx=J_xdu,dy=J_ydv\] \[f_X(x)J_X(u)=f_U(u)\] \[f_Y(y)J_Y(v)=f_V(v)\] 其中\(f_{U}\)是在\((u,v)\)空间中的一个函数，\(f_{X}\)是\(f_{U}\)在\((x,y)\)空间上的映射，对\(f_Y\)同理。
\[f_{U,V}(u,v)=f_{X,Y}(x,y)J_X(u)J_Y(v)\] 其中\(f_{U,V}\)是在\((u,v)\)空间中的一个函数，\(f_{X,Y}\)是\(f_{U,V}\)在\((x,y)\)空间上的映射。
那么有：
\[I(X,Y)=∬f_{X,Y}(x,y)log\frac{f_{X,Y(x,y)}}{f_X(x)f_Y(y)}dxdy\] 带入上述式子，有：
\[\begin{aligned} I(X,Y)&=∬f_{X,Y}(x,y)log\frac{f_{X,Y(x,y)}}{f_X(x)f_Y(y)}dxdy\\ &=∬\frac{f_{U,V}(u,v)}{J_XJ_Y}log(\frac{\frac{f_{U,V}(u,v)}{J_XJ_Y}}{\frac{f_U(u)f_V(v)}{J_XJ_Y}})J_XduJ_Ydv\\ &=∬f_{U,V}(u,v)log(\frac{f_{U,V}(u,v)}{f_U(u)f_Y(y)})dudy\\ &=I(U,V) \end{aligned} \]

从上述推导中可以知道，当且仅当映射处处可导(光滑)且可逆时，才存在雅各比行列式，才能得到上述证明。

下面折叠的部分中展示了一个用matlab编写的关于互信息这一特性的小实验。

关于互信息的小实验

在MATLAB中，两个随机变量的互信息可以通过直方图抽样估计得到：

function MI = mutual_information(X,Y)
    % 计算联合概率
    jointXY = histcounts2(X,Y,'Normalization','probability');
    % 计算边缘概率
    marginalX = sum(jointXY,2);
    marginalY = sum(jointXY,1);

    % 计算互信息
    MI = 0;
    for i = 1:length(marginalX)
        for j = 1:length(marginalY)
            if jointXY(i,j) ~= 0
                MI = MI + jointXY(i,j)/numel(jointXY) * log2(jointXY(i,j) * numel(jointXY)/(marginalX(i)*marginalY(j)));
            end
        end
    end
end

假设数据集\(\{X,Y\}\)符合规律\(y=e^{2x}+x\)，现在检验各种不同的个体结构与真实规律的互信息：

x = [0:0.01:1000];x = [0:0.01:1000];
y_target = exp(2*x)+x;
y_tree_1 = exp(2*x);
y_tree_2 = exp(2*x)+1;
y_tree_3 = exp(x);
y_tree_4 = x;
y_tree_5 = 2*x+1;
y_tree_6 = 2*exp(x);
y_tree_7 = power(exp(x),2);
y_tree_8 = power(exp(x)+x,100);
y_tree_9 = sin(x);
y_tree_90 = power(x,2);
y_tree_rand = randi(12308,1,100001);
y_tree_de = 2*exp(2*x)+1;

mi_tree_target = mutual_information(y_target,y_target); % 输出的信息熵
mi_tree_rand = mutual_information(y_tree_rand,y_target)/mi_tree_target;
mi_tree_1 = mutual_information(y_tree_1,y_target)/mi_tree_target;
mi_tree_2 = mutual_information(y_tree_2,y_target)/mi_tree_target;
mi_tree_3 = mutual_information(y_tree_3,y_target)/mi_tree_target;
mi_tree_4 = mutual_information(y_tree_4,y_target)/mi_tree_target;
mi_tree_5 = mutual_information(y_tree_5,y_target)/mi_tree_target;
mi_tree_6 = mutual_information(y_tree_6,y_target)/mi_tree_target;
mi_tree_7 = mutual_information(y_tree_7,y_target)/mi_tree_target;
mi_tree_8 = mutual_information(y_tree_8,y_target)/mi_tree_target;
mi_tree_9 = mutual_information(y_tree_9,y_target)/mi_tree_target;
mi_tree_90 = mutual_information(y_tree_90,y_target)/mi_tree_target;
mi_tree_de = mutual_information(y_tree_de,y_target)/mi_tree_target;

结果如下：

编号	归一化互信息的值
1	1
2	0.2674
3	1
4	0.2832
5	0.2409
6	1
7	1
8	0.017
9	0.3223
90	0.2674
de	1
rand	0.2674

此处使用互信息的原因有两个：

• 利用互信息的可逆性，SBGP可以在进化的早期就可以识别到潜在的building blocks.

  在SBGP的一系列论文中，building blocks被认为是最终解的某些片段。利用互信息的可逆性，与这些子树语义表现相似的子树可以在进化的早期就被识别到。

  需要注意的是，如果两个子树的结构相同，其对目标的语义相似程度（也就是互信息的值）是相等的。但是互信息相等的子树并不意味着子树的结构是相同的。

• 基于误差的fitness无法正确奖励对最终解有贡献的building blocks。（fitness无法聚焦到一个个体上）相比于fitness，互信息可以相对安全的移除倍数和加法关系对个体或者building blocks结构的改变。基于误差的fitness对于公式的细节结构（比如常数项）过于敏感，导致进化的进程不太能关注公式中的基本结构和building blocks

但是，互信息所描述的个体与目标之间的关系过于抽象，因此无法作为直接度量个体fitness的标准。

语义的building blocks和语义模式

由于将结构的空间投射到了新的语义空间，因此作者重新定义了building blocks和schema。
在语义的空间中，结构相似的个体的语义未必相近，反之亦然。无法再像之前的定义通过结构的相似直接提取schema，因此此处作者采用的方法是首先将语义相同的子树归纳为building blocks，再从building blocks构建schema。

语义的building blocks

作者认为，语义的building blocks(semantic building blocks)是满足下列三个条件的子树：

• 高语义值
• 该语义值在所有子树的语义值分布中出现频率高
• 子树的大小不能超过某个阈值

语义模式

Schema可以看做是若干building blocks按照某种规律进行特定组合构成的building blocks的集合。因此，此处作者定义一个语义schema由两部分组成：

• building blocks的集合
  
• 描述building blocks在schema内部分布特征的函数，以便判断哪些个体属于这个schema
  如果一个个体的building blocks的分布特征符合这个函数，那么这个个体就属于对应的这个schema.

SBGP

概览

根据语义building block和语义schema的定义，作者在^[3]中提出了SBGP(semantic Building block GP)。

SBGP的核心思想是从种群中正确识别出building blocks，再将building blocks组建为schema，然后搜索空间中的搜索进程将主要在某个schema子空间中进行。另外，为了保证算法不会陷入局部最优，SBGP中还设计了一些机制用于保护种群中的基因多样性。

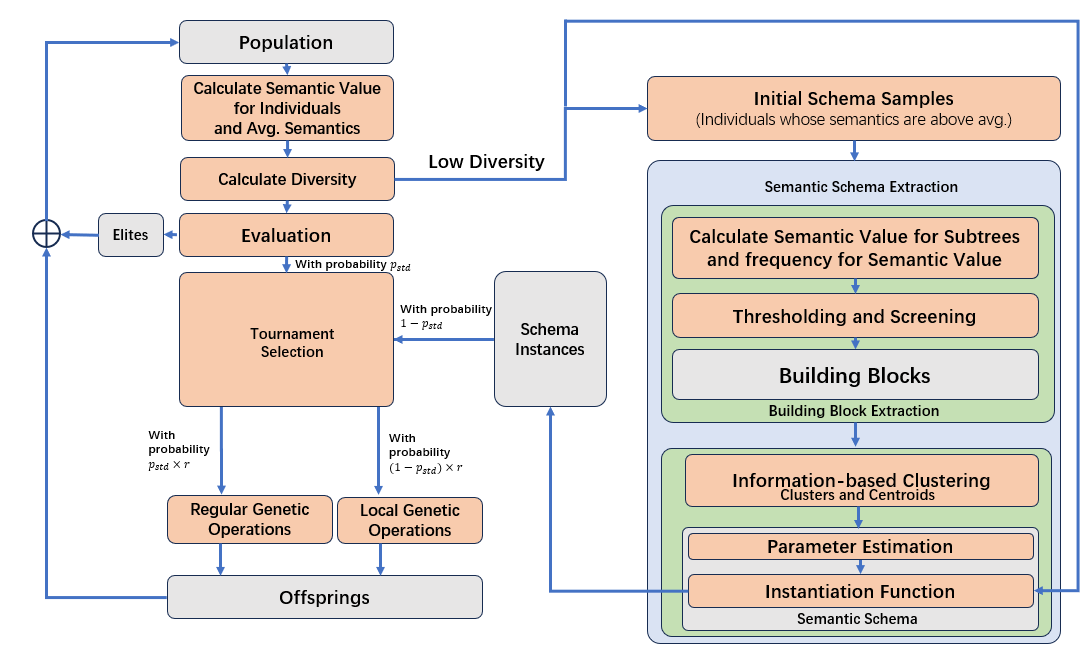
SBGP的算法流程由上图所示，对传统遗传编程的改进如下：对语义schema的提取和实例化、局部的遗传操作。

语义building blocks的提取

语义的schema无法被直接通过结构上的相似性进行提取，而是通过语义的building blocks进行构建。作者认为语义的building blocks是满足 之前提到的定义的子树。
提取语义的building blocks的方法如下：
1. 计算整个种群中所有个体的语义值和平均语义值，筛选出语义值高于平均语义值的个体
2. 为了筛选符合条件的子树，需要计算符合大小限制的当前种群中所有子树的语义值和相同语义值的子树的出现频率。因此，每一个（大小在限定范围内的）子树都记录了两个信息：其语义值和以及出现频率
3. 具有高语义值和高出现频率的个体将会被视作语义的building blocks

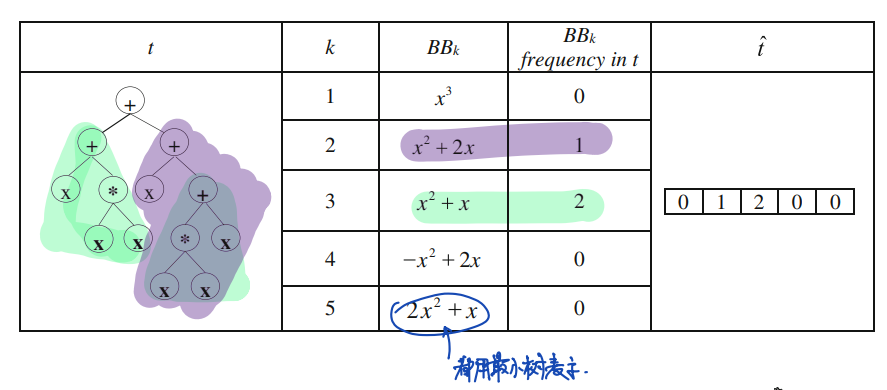
最小语义树

最小语义树(semantic representative tree)指的是在语义相同的树当中大小最小的一棵树。最小语义树用于衡量某个语义值下的子树是否可以满足大小条件成为building block。

全过程伪代码如下：

C: cluster of Trees
minS: minimum acceptable semantic similarity for building blocks
maxFrequencyRank: maximum acceptable frequency rank for building blocks
minBlockSize: minimum acceptable size for building blocks

for each semantic value S in C:
    freq = number of occurrences of all subtrees in C having semantic value = S
    srt = the smallest subtree having semantic value of S # 最小树的定义在[3]中未被使用
    add <S,freq,srt> to SList
end
sort SList according to freq
rank = 0
for each semantic value S in SList:
    if S > minS && size(SList(S).srt)>minBlockSize && rank < maxFrequencyRank
        add srt to blockList
        rank++
    end
end
return blockList

语义Schema的提取

按照定义，一个语义schema指的是一组building blocks聚类的集合，作者认为每一个聚类中的building blocks具有高度的相关性。并且这些building blocks在schema中的分布需要确定。在^[1]和^[2]中作者使用了不同的方法对building blocks进行归类。

基于聚类的提取方式

激活的building blocks

对于一棵树\(t\)，其输出为\(T\)；\(t\)中的一颗子树\(t_{sub}\)的输出为\(T_{sub}\)，并且其语义值\(S(t_{sub})\)与某个building block的语义值相同\(S(BB_i)\)，即\(S(t_{sub})=S(BB_i)\)。如果\(T_{sub}\)与\(T\)的互信息\(I(T;T_{sub})\)非常高，那么称这个building block为高活性的building block(active building block)。
用\(\beta(t)\)表示某一个个体\(t\)的所有激活的building blocks的合集。

基于信息的聚类

作者在^[2]中使用了基于信息的聚类(information based clustering)，聚类算法试图将所有的building blocks按照相似程度和相关性程度归为几个类，每一个类的聚类中心可以提供关于最终解的足够多的信息。简言之，聚类算法可以进一步的浓缩这些具有高语义值的个体的特征，并将特征用聚类中心表示。
这种聚类算法需要达成三个要求：

• 每两个聚类中心\(c_i\)与\(c_j\)之间的互信息应当是最小的： \[\min_{C=\{c_1,...,c_k\}}I(c_i.c_j),∀i,j∈C,i≠j\]
• 每个聚类内部的元素与聚类中心的互信息应该是最大的：
  \[\max_{L=\{l(BB_i)|i=1,2,...,n\}}I(BB_i;c_{l(BB_i)}),∀i=1,2,...,n\] 其中\(l(BB_i)\)指某个building block\(BB_i\)所属的聚类的编号。\(L\)是一个含有所有\(l\)的列表。
  
• 所有聚类中心的平均语义信息需要最高：
  \[\max_{C=\{c_1,...,c_k\}}\frac{1}{k}\sum_{i=1}^kS(c_i)\] 这个设计的目的是因为SBGP中感兴趣的是具有高语义值的聚类中心，这些中心可以提供足够多的关于最终解的信息：\(I(c_1,c_2,...,c_k;Y)\).

整个聚类的方法分为两步：寻找聚类中心和将其他的building blocks依附到聚类上。

• 寻找聚类中心的方法是：对于一个给出的Building block的集合，移除一个building block，然后计算剩余的building block 构成的子集\(C_r\)中的平均语义值和子集中的平均互信息值之比\(θ(C_r)\):
  \[θ(C_r)=\frac{\frac{1}{k}\sum_{BB∈C_r}S(BB)}{\frac{2}{k(k-1)}\sum_{BB_i ∈ C_r}\sum_{BB_j∈C_r}I(BB_i;BB_j)},j=i+1\] 这个式子中\(θ(C_r)\)的值越高，说明子集中样本种类丰富(样本内部的互信息低)的同时，整体的语义值还非常高。
  要求每次移除的building blocks都需要使得\(θ(C_r)\)最大，也就是说，每一次“移除一个building blocks”的操作首先都需要尝试计算移除每一个building block后的\(θ(C_r)\)，然后再真正地移除导致最大\(θ(C_r)\)的那个building blocks。
  这个过程会一直重复，直到\(θ(C_r)\)满足：
  \[\frac{θ(C_r)-\overline{θ}}{\overline{θ}}>δ\] 其中\(\overline{θ}\)是此前所有循环中记录的过去每一循环中最大的\(θ(C_r)\)的平均值。 如此，最终剩下的building blocks将作为聚类的中心。
  如果最终只剩下了两个building blocks，将测量他们的互信息，如果两者互信息高则选取语义值较高的building block作为聚类中心，否则两者都将作为聚类中心。这种情况下需要搜索更多的building blocks。
  
• 然后计算除了聚类中心之外所有的building blocks对于所有聚类中心的互信息，选取具有最大互信息的聚类中心作为这个building block所属的类。
  \[I(BB)=arg max_{i}(I(BB_i;c_i)),c_i∈C\]

实例化函数

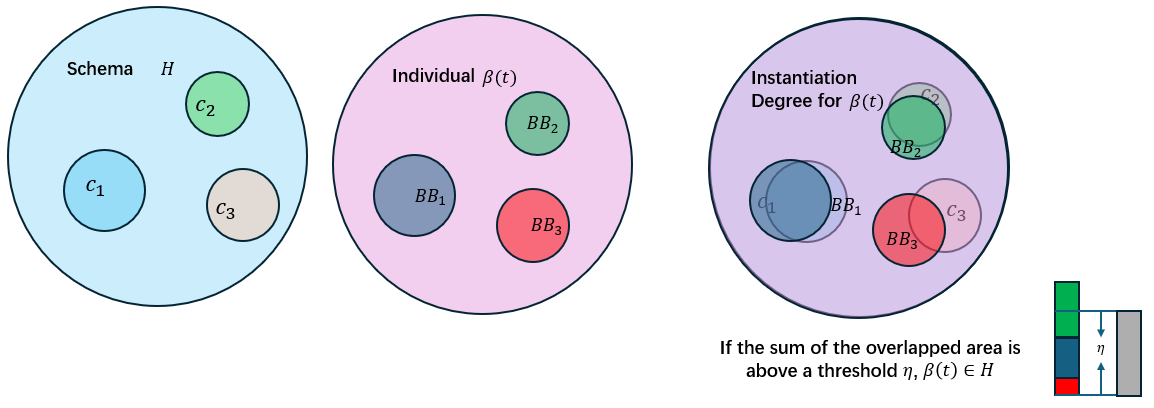
实例化函数(instantiation function)用于决定给定的种群中哪些个体属于特定的schema，它的概念近似于隶属度函数。实例化函数的思路是找该个体中所有的active building blocks对于所在的聚类的隶属程度，如果隶属度大于某个阈值\(η\)，那么这个个体是这个聚类对应的schema的一个实例化。
一个building block \(BB\)对其聚类中心\(c_{l(BB)}\)的作用表示为：
\[E(BB)=\frac{S(BB)I(BB; c_{L(BB)})}{∑_{i=1,i≠c_{L(BB)}}I(BB;c_i)}\] 定义一个个体的实例化程度表示为其内部所有的active building blocks对每个cluster的最大贡献值的和，并用聚类中心自身的作用的和作为归一化：
\[μ(β(t))=\frac{\sum_{i=1}^k \max_{BB∈β(t)}E(BB),i=l(BB)}{\sum_{i=1}^kE(c_i)}\] 因此，一个语义schema可以表示为：
\[H=[\{c_1,c_2,...,c_k\}∼μ(β(t))]\]

基于概率分布的提取方式

Building block的表示空间

基于概率分布的提取方式在^[1]中使用，随后在^[2]中被弃用改为使用聚类算法浓缩遗传信息。这种方式试图用building blocks构建一个一维的空间，在这个空间中每个个体都表示为一个向量，向量中的每个元素表示该个体中某个building blocks的出现个数：

（需要注意的是，这种表示方式与building block在个体中实际存在的位置无关）

用数学表示简单表示为：
\[t→\hat{t}\] \[C→Ω\] \[Ω=\{\hat{t}|\hat{t}[i]=freq(BB_i), i=1,..,k\}\] 其中\(freq(BB_i)\)表示的是一个building block \(BB_i\)在某个个体中的出现频数。
在这个空间中可以根据个体中是否含有某个building block来划分相应的子空间，记\(Ω^{s}\)表示含有building block \(s\)的所有个体构成的集合，有：
\[Ω=Ω^{\{1,2,3,...,k+1\}}=U\Omega^s,Ω^s=\{\hat{t}|∀j∈s,\hat{t}[j]≠0\}\]

参数估计

这种方法使用了统计学的参数描述了语义building blocks在一个schema中的分布情况。
假设building block \(s\)中对应的个体中所有building blocks的语义分布服从多元正态分布：
\[Ω^s∼N_{|s|}(μ_s,Σ_s)\] 注意\(μ_s\)和\(Σ_s\)是两个向量。
其中\(|s|\)为\(BB_i\)中找到的个体数（样本数）；有对该分布均值和方差的估计如下：
\[μ_s=\frac{1}{\sum_{i=1}^{|Ω^s|}S(\hat{t_i})}\sum_{i=1}^{|Ω^s|}\hat{t_i}S(\hat{t_i})\] 其中的\(\hat{t_s}\)就是指表示该个体的向量。 \[Σ_s=\frac{1}{\sum_{i=1}^{|Ω^s|}S(\hat{t_i})}\sum_{i=1}^{|Ω^s|}(\hat{t_i}-μ_s)(\hat{t_i}-μ_s)^T.S(\hat{t_i})\] 除了多元正态分布的均值和方差之外，这种方法还根据树的语义值赋予了权重，并采用了最大值归一化：
\[φ_s=\frac{\sum_{\hat{t}∈Ω^s}S(\hat{t})}{Max(\varphi)}\]

其中，\(φ_s\)对应的是某个building block \(s\)的权重，\(\sum_{\hat{t}∈Ω^s}S(\hat{t})\)表示的是\(Ω^s\)中所有个体的语义值之和。
那么，一个building block子空间的特征可以表示为：
\[\lambda_s=\{\varphi_s,μ_s,\Sigma_s\}\] 那么（由于种群中只存在一个schema）schema的分布特征可以表示为：
\[λ=\{λ_s\},s∈\{1,2,...,k\}\] 对于一个个体\(\hat{t}\)，其符合该分布特征\(λ\)的概率可以表示为：
\[p(\hat{t}|λ)=\sum_{i=1}^Mφ_iN_{|s_i|}(μ_{s_i},Σ_{s_i})\] 因此种群中的schema可以表示为：
\[H=[\{B_1,B_2,...,B_k\}∼p(\hat{t}|λ)]\]

语义schema的实例化

当这个树的实例化程度大于设定的阈值\(η\)时，这个树是schema \(H\)的实例化：
\[μ(β(t))>η→t∈H\] 或者：
\[p(t|λ)>η\] 其中\(η\)是最初种群中高于平均语义的个体的实例化程度的平均值:
\[η=\frac{\sum^M_{t_i∈\{\text{above average ss instances}\}}μ(t_i)}{M}\]

需要注意的是，在进化的过程中，自始至终每一代种群都只能提取出一个schema。

Schema内部的遗传操作

SBGP的搜索思路是，在语义空间中对每一个语义schema内部的子空间进行完全的搜索，当该子空间的搜索进行的差不多时(用多样性，Diversity来表示)，移动到下一个schema的子空间进行搜索。
为此，SBGP中使用了局部的遗传操作(local genetic operations)来搜索子空间，使用全局的遗传操作实现从一个子空间到另一个子空间的跳跃。

为此，SBGP中设计了四种不同的局部遗传操作：

• 间接局部重组(Indirect local recombination operator, ILRO)
  这种重组是一个单后代重组，对于来自schema的两个亲本，产生的后代至少要有一个在schema当中。如果两个后代都在schema中，则选取语义值高的那个加入到后代当中。
  ILRO实现的方式是试错：首先两个亲本的交叉点选择需要不断尝试，以至于两个亲本交叉点下方的语义值是相同的，然后才进行交叉。其次，如果交叉的结果是没有任何后代在schema中，那么则尝试选取新的交叉点和新的亲本。
  
• 间接局部突变(Indirect local mutation operator, ILMO)
  这种突变的亲本来自于某个schema，随机在这个亲本上选择一个突变点，并用生成的子树替换这个突变点下方的子树。这个新的子树从schema的building blocks中生成。DLMO也需要试错：突变结束后需要检查后代是否在这个schema中，如果不在，那么舍弃这个后代结果。
  
• 直接局部突变(Direct local mutation operator, DLMO)
  这个操作会随机的选择一个亲本进行突变，然后检查突变点上方的部分存在的building blocks，接着移除这个building blocks所属的聚类，从其他的聚类中挑选building blocks生成新的树。生成过程到整个后代达到最大深度为止。
  
• 无亲本繁殖(Parentless child production operator, PCPO)
  无亲本繁殖的目的是为了直接从schema中生成个体。这个个体从端点集和building blocks组成的并集中随机生成。当一个building block从随机选择的一个聚类中挑选出来构成个体后，这个聚类中的其他building blocks将不能再用于生成该个体。

子空间转换和多样性的控制

多样性与子空间内部搜索的控制

SBGP移动到下一个schema子空间的时机由现有种群的多样性进行表征：只有在现有种群的多样性处于低水平时，搜索才会从现在的schema转移到新的schema中，这个过程称之为schema transition。
现有种群的多样性可以由现有种群中语义值的标准差表示：
\[diversity(pop)=\sqrt{\frac{1}{popsize}\sum_{i ∈pop}(S(i)-\overline{S})^2}\] 其中\(\overline{S}\)表示现有种群\(pop\)的平均语义值。
\(diverisityRatio\)进一步对最近\(w\)代内种群的多样性使用了滑动窗口平均，窗口的大小为\(w\)：
\[diversityRation=\frac{diverisity(pop(g))}{\frac{1}{|w|}\sum_{i=1}^w diversity(pop(g-i))}\] 其中\(pop(g)\)表示第\(g\)代的种群；\(pop(g-i)\)表示第\(g-i\)代的种群，\(i\)的最大上限为\(w\)。
当\(diversityRatio\)低于设定的阈值时，将重新对现有的种群提取building blocks和schema。由于现有的种群的表现一定比上一次提取时种群的表现更好，因此理论上提取的schema的表现也会更好。
在^[3]中，这个阈值被设定为一个较高的水平(0.9)以保证不会陷入局部最优解。

标准遗传操作

除了使用局部的遗传操作之外，针对于种群中所有个体的标准遗传操作也使用于保证种群中的多样性，每一次迭代中，标准遗传操作的概率与多样性有关，表示为：
\[p_{std}=-\frac{log(diversity(pop))}{10}\] 根据一些数学推导可以发现此时准群中语义的标准差应当在\((0,1)\)之间，代表种群中个体的语义分布不会过于分散。

泛化

SBGP中的一个比较大的问题在于泛化：因为语义值的设定只和生成的数据和真实数据的差异有关。因此，SBGP中使用了测试集提高泛化能力。在每一代当中，虽然个体的表现是通过个体输出和训练集之间的误差来进行衡量的，但是也会衡量测试集与每一代中表现最好的个体的输出之间的误差\(error(best,V)\)。如果当前这一代的测试集误差大于之前一代的测试集误差，则表示出现了过拟合。因为在过拟合的情况下，再多的训练会增加测试误差。
其二的操作是使用了精英策略(elitism)。

SBGP的整体运行流程

SBGP整体的运行流程描述如下：

• 对于种群，首先衡量其中每个个体的适应度，并保留种群中适应度较好的个体进入精英列表。
  
• 计算种群中的多样性，如果多样性\(DiversityRation\)低于设定的阈值，则从现有的种群中抽出一个schema，子空间的搜索将转移到这个schema中进行。通过这个schema的实例化函数，可以计算现有种群里所有个体的实例化程度，并判断种群中的哪些个体属于这个schema。
  
• 在发生交叉的概率条件下，有\(P_{std}\)的概率发生针对于全局所有个体的标准交叉：如此亲本个体将会通过锦标赛选择的方式选择出，然后进行标准交叉。
  同时，有\(1-P_{std}\)的概率发生仅针对于schema的实例化个体的局部交叉：所有该schema实例化的个体将会通过锦标赛选择的方式选择出，然后进行间接局部重组。
  
• 在发生突变的概率条件下，有\(P_{std}\)的概率发生针对于全局所有个体的标准突变：突变的亲本通过锦标赛的方式选择出。有\(1-P_{std}\)的概率发生间接或者直接的局部突变。
  如果不发生变异，则进行无亲本繁殖。
  
• 遗传操作的后代将会和精英一同加入下一代的种群。

现在SBGP存在的一些问题：

• 互信息抽象描述的可解释性不高 （比如两个个体具有相同的语义值，但是其内部哪一部分贡献了百分之多少的语义值无从得知）
  
• 语义空间中的操作和fitness空间中的操作的对应关系

1. Zahra et al, Semantic Schema theory for genetic programming, Apply Intelligence, 2016. ↩︎
2. Zahra et al, Semantic Schema modeling for genetic programming using clustering of building blocks, Apply Intelligence, 2018. ↩︎
3. Zahra et al., Semantic schema based genetic programming for symbolic regreSion, Applied Soft Computing, 2022. ↩︎
4. Alexander et al., Estimating mutual information, Physical Review, 2004. ↩︎