ROC聚类算法

Machine-Component Group Formation in Group Technology, John R King, 1979.
Machine-component grouping in production flow analysis: an approach using a rank order clustering algorithm, John R King, 1980.
Modified Rank Order Clustering Algorithm Approach by Including Manufacturing Data, Nagdev Amruthnath et al. 2016
ROC及其改进的ROC算法的代码（R语言）：https://www.iamnagdev.com/?p=488

分组

分组(grouping)是工业流程分析中的一个重要手段，分组可以找到需要进行相同步骤和经过相同机器处理的零部件，从而将它们一并生产，提高生产效率。Burbidge于1963年提出了一种称之为生产流分析(production flow analysis)的分组方法，这种分组方法不需要对系统进行编码，过程也比较简单。这个方法的步骤可以简要地描述为：
- 将机器进行分类：能够进行类似操作、需要部件相同的机器归为一类。
- 检查生产过程和清单，确认对于每个部件，要进行的操作以及进行这些操作所需的机器。
- 分析生产流，将生产流分解为若干主要的机器-部件组。
整个生产流所需要的机器和部件可以使用混淆矩阵进行表示：混淆矩阵的列\(I\)表示某个零部件(parts)，矩阵的行\(J\)表示生产该零件所需要的机器。矩阵内元素的值为二进制：如果某个元素的值为\(x_{ij}=0\)，代表对应零件\(i\)生产不需要机器\(j\)。如果某个元素的值为\(x_{ij}=1\)，则代表对应生产对应的零件\(i\)需要机器\(j\)。
完成后的混淆矩阵如下图所示: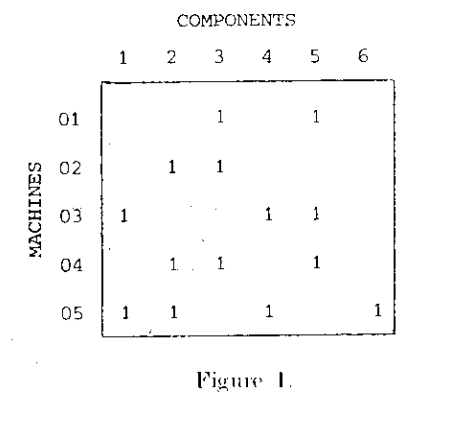

进一步地，通过对混淆矩阵中行和列顺序的排位，可以进一步找到需要经过同样机器生产的不同零部件，进而将它们归为一组进行生产，提高生产效率。

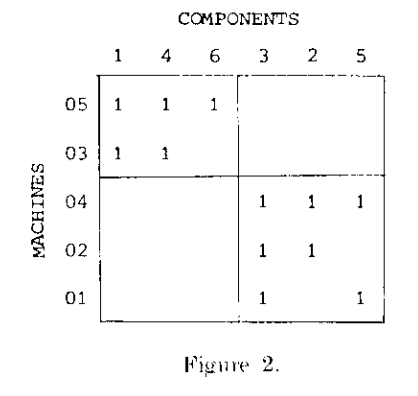
最早这样对混淆矩阵行列的排序是通过手工完成的。手工排序的方法可以应付维度小的混淆矩阵， 但当应用于大问题时，手工排序非常耗时，容易出错。因此，解决混淆矩阵排序的两种算法：单链接聚类(single linkage clustering)和结合能聚类(bond energe clustering)分别于1968年和1972年提出。 下面将回顾这两种方法。

既有方法

单链接聚类

单链接聚类是一种分级聚类(hierarchical clustering)技术，它依赖于相似度的计算。简单来说，在单链接聚类中，定义两个机器的相似度(similarity)为相同部件的个数\(N_s\)与两者所需要的所有部件数（相同部件只算一次）\(N_c\)之比：
\[S=\frac{N_s}{N_c}\] 比如对于机器01和02而言，其共同处理的部件为3，两个机器所处理的全部部件为：2，3，5，因此01和02的相似度为\(S_{01,02}=\frac{1}{3}=0.33\)。
同理可以计算出所有可能的两两机器之间的相似度。
下表列出了Figure1中所有机器的相似度：

然后，根据相似度绘制出聚类树状图(Dendrogram)：聚类树状图的横轴是不同的机器，纵轴是它们的相似度。具体绘制的方法以上表为例：
- 首先找到相似度最大的三组:(03,05),(01,04),(02,04)，分别用二叉树对这三者进行连接，完成第一次聚类。第一次聚类即为上述的三组。
- 然后找到相似度第二大的一组(02,01)，用二叉树将含有01和02的两个第一次聚类的类别连接，完成第二次聚类。第二次聚类的结果为(02,04,01)一组，(03,05)一组。
- 最后根据相似度为0的组用二叉树将(02,04,01)与(03,05)用相似度为0连接。

在Python中可以使用scipy.cluster中的hierarchy.linkage()函数作图。

绘制好的聚类树状图如下图所示：

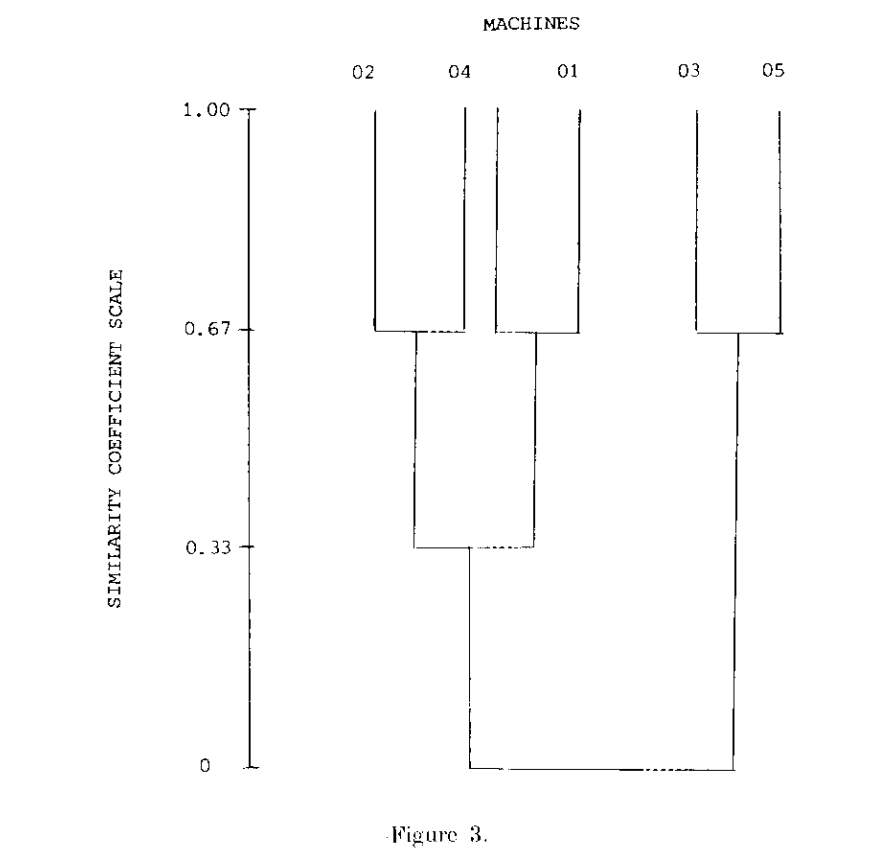
根据图上可以找到需要的聚类层次，此处选择第二次聚类的结果：即(02,04,01)一组，(03,05)一组。并依据聚类结果对混淆矩阵的行列重新排序，得到：

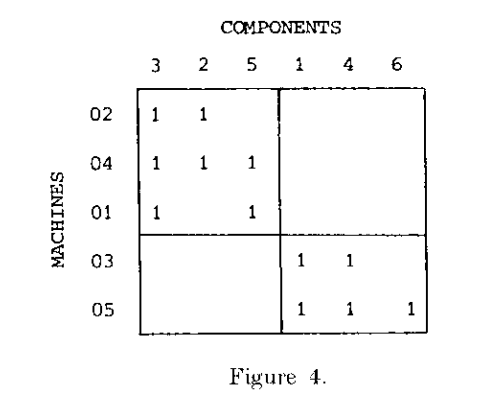
单链接聚类在混淆矩阵建立完成后需要对其进行二次处理和重新绘图，过程较为复杂。

结合能聚类

结合能聚类方法的基础思想基于化学中的结合能概念，在这种方法中，定义行/列的结合能为：对于矩阵中某一为1的元素\(x_{ij}=1\)，如果其相邻行/列\(x_{i,j+1}\)或\(x_{i+1,j}=1\)，那么该元素所在的行/列结合能加1。总结合能等于所有行结合能与列结合能之和。
例如下图展示了figure1的结合能：

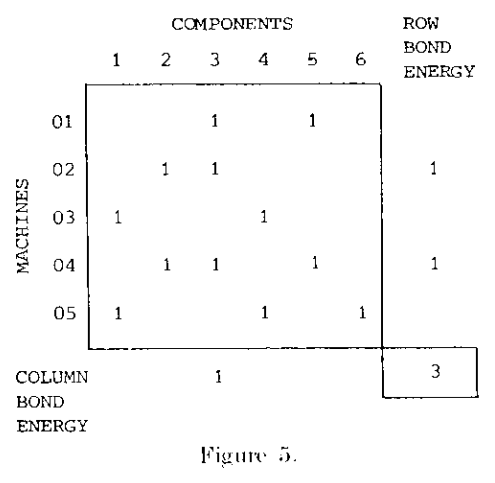
通过用结合能表示相邻1的元素个数，使得行列排序问题被转化为了最优化问题：通过行列排序使得整个矩阵的总结合能达到最大即可。
结合能算法使用了一种复杂的迭代过程，描述如下：
- 任意移动一列，并令\(i=1\) - 尝试分别移动其他的\(N-i\)列到\(i+1\)中可能的位置中，计算每一列的结合能。找到此时可以给出最大结合能的位置移动方法。然后\(i+1\)，重复上述操作直到\(i=N\)。（\(N\)是矩阵的列数）。
- 对行也重复上述的迭代过程，令\(j\)从\(j=1\)一直迭代到\(j=M\)。（\(M\)是矩阵的行数）。

结合能聚类方法对figure1的聚类结果如下，可以发现其聚类结果基本上和单链接聚类是相同的。

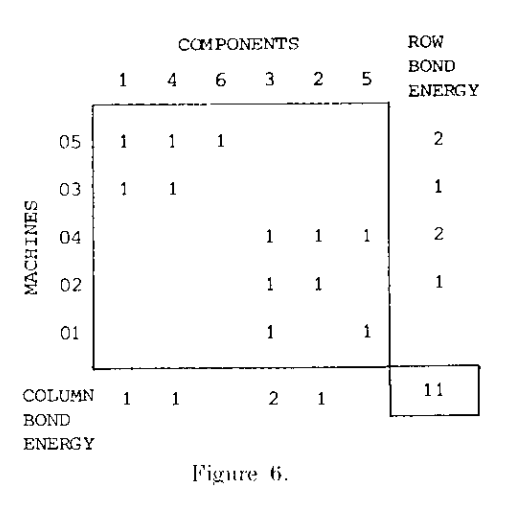
可以发现，这种算法对最初随机选取的列和行的位置十分敏感，而且计算量巨大。

ROC聚类的方法论

ROC聚类步骤

假设对部件和混淆矩阵已经建立：
1. 对每一行机器，将每一行的01组合视为一个二进制编码，并转换为十进制。根据十进制大小为每一行赋予一个等级(rank)。如果两行的十进制大小相同，那么在上的一行被赋予更高的等级。
2. 检查现在矩阵的各行是否是按照等级从大到小的顺序排列。
- 如果是，则停止算法。
- 如果不是，则跳到3.
3. 按照十进制大小从大到小重新排列每一行的顺序。
对每一列部件，将每一列的01组合视为一个二进制编码，并转换为十进制。根据十进制大小为每一列赋予一个等级。如果两列的十进制大小相同，那么在左的一行被赋予更高的等级。
4. 检查现在矩阵的各列是否是按照等级从大到小的顺序排列。
- 如果是，则停止算法。
- 如果不是，则跳到5.
5. 按照十进制大小从大到小重新排列每一列的顺序。

下图表示了使用ROC算法对figure1的矩阵行列进行排序的迭代过程：

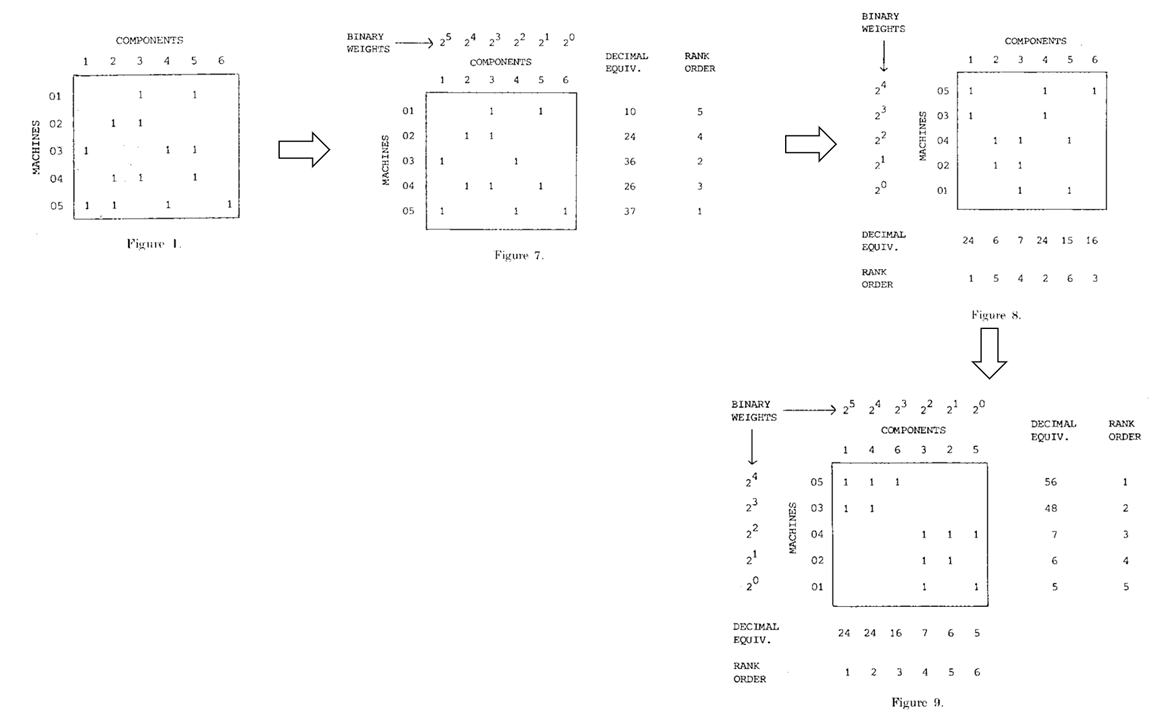
计算机在执行ROC算法时，为了进一步节约计算量，并不需要将二进制编码转换为十进制再比较大小，而是可以通过从高位到低位，逐位比较的方法直接对二进制编码的大小进行比较。
可以发现，相比于结合能和单链接算法，ROC算法的计算量更小，算法达到收敛的时间也更快。

例外元素

在聚类结束之后，有时混淆矩阵会出现不属于任何类的“1”元素，这样的元素称为例外元素(exceptional elements).

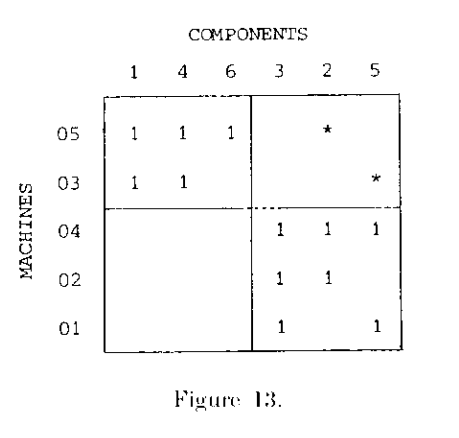
如上图所示，聚类结束后标⋆位置的两个“1”不属于任何一类，是例外元素。
对于这些例外元素，原作者认为如果聚类结束后出现了例外元素，应当将其在最初的矩阵中删除，然后重新进行ROC聚类。
这些例外元素应当采用集中化的生产方式或者直接购买这些部件，而非使用细胞生产。

关键机器

在论文中，作者还考虑到了一种情况：如果非常多的组件都需要经过同一个机器操作，那么这样的机器就称为关键机器(bottleneck machines)，关键机器决定了生产效率。在论文中，作者建议如果出现关键机器，可以在生产中增加若干个相同的这个机器，同时在混淆矩阵中将这个关键机器所在的行拆分为若干行，拆分方法如下图所示：

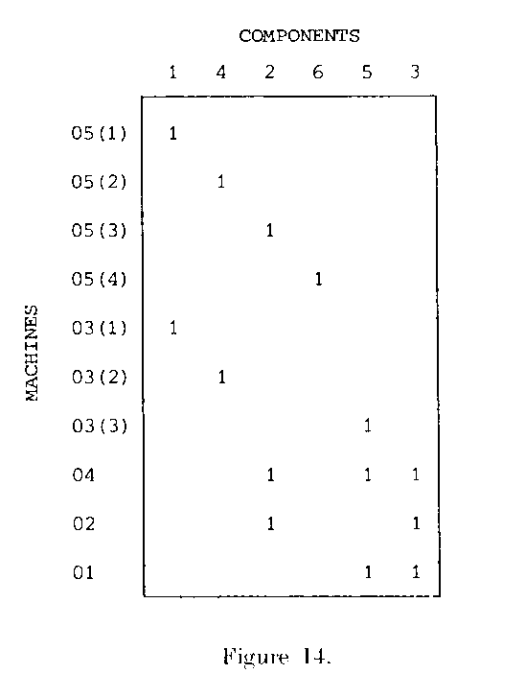
如上图，例如对于figure1，可以将机器05和03所在行分别拆分为若干行，每一行只含有一个“1”元素，再进行聚类，聚类结果如下图所示：

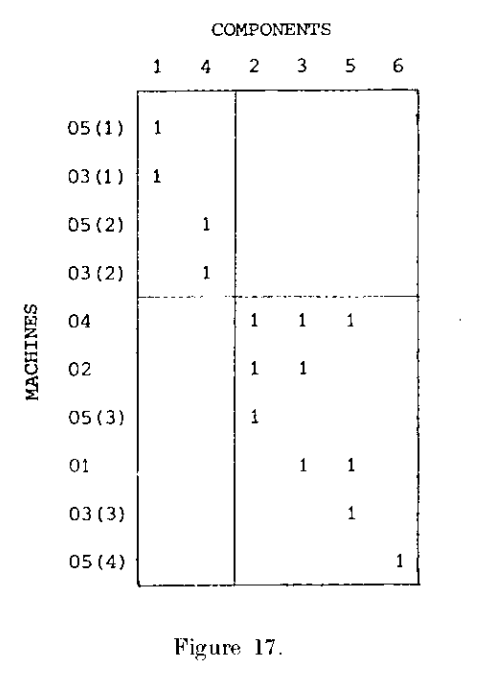
对于左上角的类，又可以将相同的机器进行合并，最终得到：

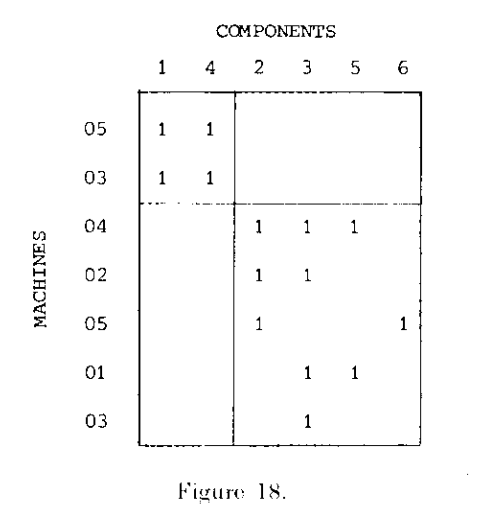
改进

对ROC算法的评价

结合能算法和单链接算法在最初的混淆矩阵建立完成后还需要对数据进行二次处理，其中结合能算法还包含复杂的迭代过程，这两种算法的过程和计算量都相对较为复杂，而ROC算法在混淆矩阵建立后不需要对数据再进行二次处理，只是简单地设计了一种方法为混淆矩阵进行排序，在计算量和算法复杂度方面相比前两者更加简单。
但是，ROC算法只是一个排序算法而非优化过程，所以产生的解决方案是由初始矩阵的形式决定的。
例如下图的例子：

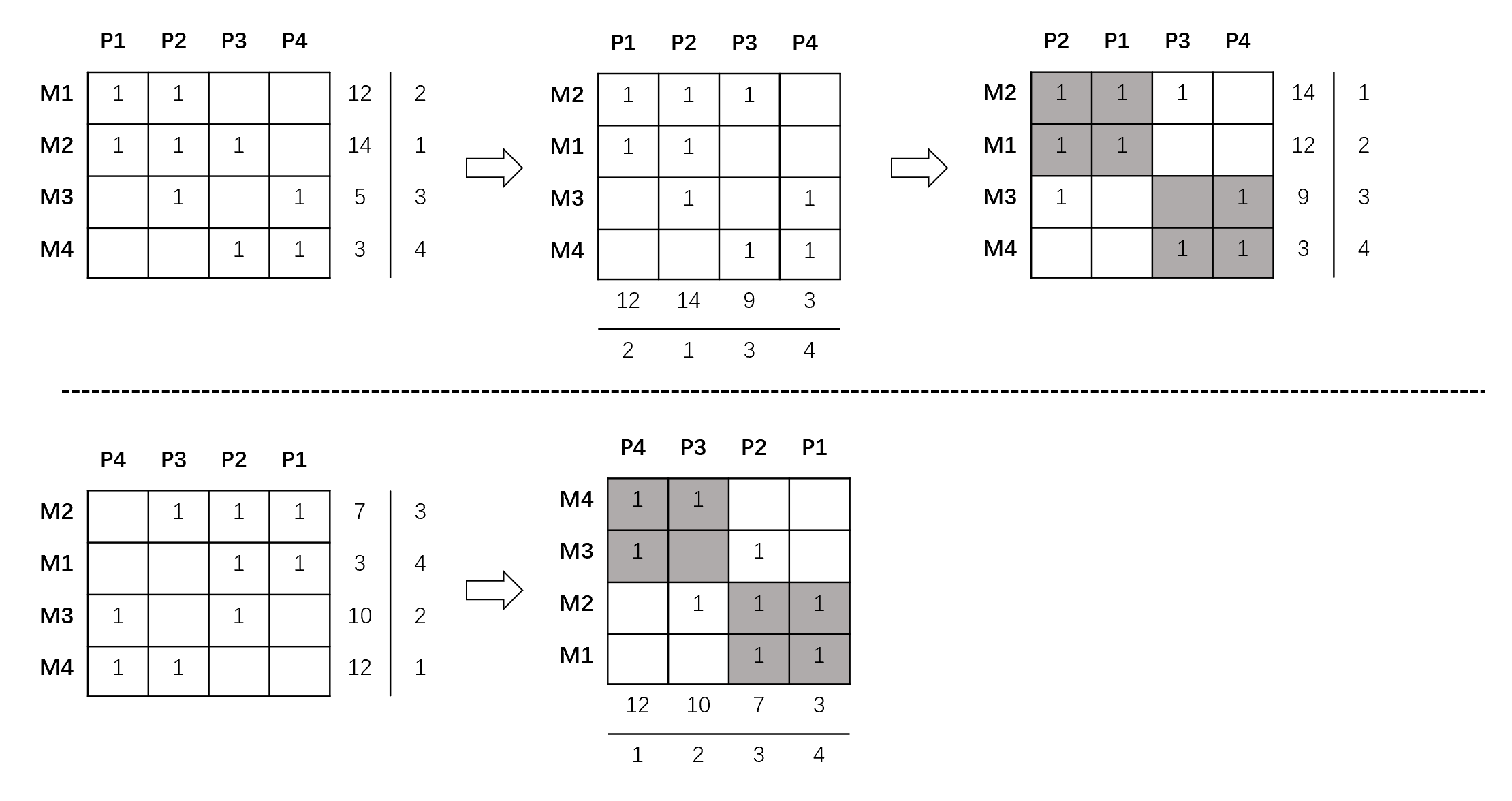
可以发现如果初始的混淆矩阵形态不同，那么最终稳定时的矩阵是不同的。如何决定最原始的混淆矩阵中机器和部件的排序也是一个问题。

改进的ROC算法

ROC算法是一种简单的混淆矩阵排序算法。“Modified Rank Order Clustering Algorithm Approach by Including Manufacturing Data”一文的作者提出ROC算法的执行过于理想化：实际生产中不可能所有的机器生产效率和工作情况完全相同，而ROC算法中没有包含任何有关于机器和零部件状态的生产数据。因此，该作者根据生产数据，对混淆矩阵中的每一个机器和部件都赋予了权重。矩阵中每一个元素可以根据对应机器和零部件的循环时间(cycle time，生产线上每相邻两个产品产出的时间)、可靠性、以及设置时间为其赋予权重。该论文中根据循环时间和产率为每个机器赋予了权重，具体而言，每一个机器的权重\(n_{wi}\)为：
\[n_{wi}=\frac{CT_i}{∑CT_i}+\frac{PV_i}{∑PV}\] 其中\(CT_i\)为机器\(i\)的循环时间；\(PV_i\)为机器\(i\)的产率。由于单位不同，对二者均做了归一化处理。
也可以根据相应的生产数据为每个部件赋予权重\(n_{wj}\)，但是论文中并没有给出具体的例子进行说明。

改进后的ROC算法的执行步骤为：
1. 为每一个机器和每一个部件生成各自的权重\(n_{wj}\)和\(n_{wi}\)。
2. 为整个生产过程建立混淆矩阵。
3. 根据权重，按照从大到小的顺序为行列排序。
==下面的步骤与ROC算法基本相同==
4. 对每一行机器，将每一行的01组合视为一个二进制编码，并转换为十进制。根据十进制大小为每一行赋予一个等级(rank)。如果两行的十进制大小相同，那么在上的一行被赋予更高的等级。
5. 检查现在矩阵的各行是否是按照等级从大到小的顺序排列。
- 如果是，则停止算法。
- 如果不是，则跳到1.
6. 按照十进制大小从大到小重新排列每一行的顺序。
对每一列部件，将每一列的01组合视为一个二进制编码，并转换为十进制。根据十进制大小为每一列赋予一个等级。如果两列的十进制大小相同，那么在左的一行被赋予更高的等级。
7. 检查现在矩阵的各列是否是按照等级从大到小的顺序排列。
- 如果是，则停止算法。
- 如果不是，则在执行1后跳转到6.
8. 按照十进制大小从大到小重新排列每一列的顺序。

分析

由于在执行ROC算法之前加入了一步：按照权重从大到小为矩阵的行列排序，因此最终每个类中相邻元素的权重都比较接近。权重接近的好处是每个类中的机器生产部件的速率以及其他参数都差不多，整个生产系统中不会出现“短板”——即所有零部件的处理速度都大幅度受到类中处理最慢的那个机器的影响。

疑问和讨论

• ROC算法如果不采用二进制而使用其他权重对每一行/列进行转义，对结果会有多大的影响？
  
• 收敛结果和最初部件和机器所处的位置有关吗？
  • 有关。因为ROC算法只是一个排序算法而非优化过程，所以产生的解决方案是由初始矩阵的形式决定的。
    例如下图的例子：
    
    可以发现如果初始的混淆矩阵形态不同，那么最终稳定时的矩阵是不同的。但是聚类结果相似。
    
• ROC算法一定收敛吗？
  • 一定。由于每次运行完成后只判断行或者列的终止条件，算法是一定收敛的。