钢铁淬火的简单仿真

介绍

钢铁淬火(quenching)过程是将钢铁加热到奥氏体(Austenite)以上温度后快速冷却的过程，其目的是通过冷却将奥氏体向着马氏体或贝氏体转变，得到马氏体或贝氏体组织，然后配合以不同温度的回火，以大幅提高钢的强度、硬度、耐磨性、疲劳强度以及韧性等，从而满足各种机械零件和工具的不同使用要求。
在快速降温的过程中，奥氏体会转化为不同相的结晶，最后会形成马氏体(Marternsite)、贝氏体(Bainite)、珠光体(Pearlite)和铁氧体(Ferrite)的结合钢。

淬火硬度的理论分析

淬火最重要的输出参数之一是钢铁的硬度(hardness)，它由Maynier公式提出： \[H=X_MH_M+X_BH_B+(X_F+X_P)H_{F+P} \tag{1}\] 其中\(X_M\)、\(X_B\)、\(X_F\)、\(X_P\)分别是钢铁内马氏体、贝氏体、珠光体和铁氧体的体积百分数。
该公式表明经过淬火后钢铁的维氏硬度\(H\)(Vinkers)是钢铁内马氏体\(H_M\)、贝氏体\(H_B\)、珠光体和铁氧体\(H_{F+P}\)硬度的线性组合。
同时该公式根据碳当量\(CE\)（百分比）值有如下修正：
\[H=0.6X_MH_M+X_BH_B+0.7(X_F+X_P)H_{F+P},CE>1\tag{2}\] \[H=0.95X_MH_M+0.8X_BH_B+0.9(X_F+X_P)H_{F+P},CE<1 \tag{3}\]

[1] P.Maynier, J.Hollet, P.Bastien, Hardenability Concepts with Applications to Steels, AIME. New York, NY, 1978, pp. 518-544.
[2] A Computational Model for the Prediction of Steel Hardenability, M. Victor Li et al, , METALLURGICAL AND MATERIALS TRANSACTIONS B, 1998.

碳当量百分比由如下公式给出：
\[CE=C+\frac{Si}{25}+\frac{Mn+Cu}{16}+\frac{Ni}{40}+\frac{Cr}{10}+\frac{Mo}{15}+\frac{V}{10} \tag{4}\] 其中各元素符号表示各元素在钢铁试棒(Jomminy bar)中的相对质量百分比。
>[3] Estimation of hardness during heat treatment of Steels Abhaya Simha N. R et al, Metal science and heat treatment, 2020.

事实上，钢铁试棒中各种元素的含量与各种成分的硬度直接相关，比如增加碳的含量在提高钢铁的硬度降低钢铁的延展性(ductility)。
> [4] Chemical Composition of Structural Steels, 1.51 Design of Steel Structures, MIT department of Civil and Environmental Engineering, 1999.

同时论文[1]中还提到马氏体\(H_M\)、贝氏体\(H_B\)、珠光体和铁氧体\(H_{F+P}\)的维氏硬度分别由如下公式得出：
\[H_M=127+949𝐶+27𝑆𝑖+11𝑀𝑛+8𝑁𝑖+16𝐶𝑟+21𝑙𝑜𝑔𝑉𝑟 \tag{5}\] \[𝐻_𝐵=−323+185𝐶+330𝑆𝑖+153𝑀𝑛+65𝑁𝑖+144𝐶𝑟+191𝑀𝑜\] \[+(89+53𝐶−55𝑆𝑖−22𝑀𝑛−10𝑁𝑖−20𝐶𝑟−33𝑀𝑜)𝑙𝑜𝑔𝑉𝑟 \tag{6}\] \[𝐻_{𝐹+𝑃}=42+223𝐶+53𝑆𝑖+30𝑀𝑛+12.6𝑁𝑖+7𝐶𝑟+19𝑀𝑜\] \[+(10−19𝑆𝑖+4𝑁𝑖+8𝐶𝑟+130𝑉)𝑙𝑜𝑔𝑉𝑟 \tag{7}\] 其中\(V_r\)是试棒在700℃下的冷却速率，单位为℃/s。
结合式\((1)\)、\((5)\)-\((7)\)，可以得出关于试棒淬火的硬度数学模型。
这个数学模型中，有三类输入变量：
- 各种成分的体积分数
- 各类元素的质量分数
- 700℃下的冷却速率

各种成分的体积分数

一般情况下，钢铁试棒中各种成分的体积分数是通过在显微镜下观察微结构和相应的计算公式得出的。论文[4]中提到了各种成分的体积分数是关于温度的动态变化函数。本项目只需要获得淬火后冷却到室温的钢铁硬度即可，这一数据在论文[5]中有提到。论文[5]中指出，JIS-S45C钢铁在设置的不同冷却速率下，从900℃冷却到室温时各种成分的体积分数如下表所示：

冷却速率 ℃/s	铁氧体 %	珠光体 %	贝氏体 %	马氏体 %
20	5.2	35.0	43.3	16.5
30	4.2	30.1	32.5	33.2
50	0.4	7.3	11.2	81.1

[4] Onink M, Tichelaar F, Brakman C, Mittemeijer E, Zwaag S. Quantitative Analysis of the Dilatation by Decomposition of Fe-C Austenites; Calculation of Volume Change upon Transformation. International Journal of Materials Research. 1996;87(1): 24-32.
[5] Finite-element simulation of quenching incorporating improved transformation kinetics in a plain medium-carbon steel, Minsu Jung, 2011.

各种元素的质量分数

利用论文[5]中提到的数据，模拟淬火过程使用的钢材将会是直径3mm，长度10mm的JIS-S45C碳合金钢试棒，这一钢铁的元素含量在日本行业标准[6]中提到：

元素	C	Si	Mn	P	S	Ni	Cr	Cu
含量范围%	0.42-0.48	0.15-0.35	0.60-0.90	0.030max	0.035max	0.20max	0.20max	0.30max

该标准还要求S45C中的Cr和Ni的质量分数之和不能超过0.35%。 同时，标准[7]中提到了对S45C的公差容错要求：

元素	C	Si	Mn	P	S	Ni	Cr	Cu
Lower limit %	0.03	0.02(<0.3) 0.05(>0.3)	0.03	-	-	undefined	undefined	undefined
Upper limit %	0.05	0.03(<0.3) 0.05(>0.3)	0.03	0.010	0.010	undefined	undefined	undefined

[6] JIS G 4051-1979
[7] JIS G 0321:2010

容错要求如何体现有待讨论。

冷却速率

论文[5]中提到的冷却速率的单位为℃/s，此外其速率是从900℃开始降温到400℃的平均冷却速率。而公式\((5)\)-\((7)\)中的\(Vr\)是700℃时的瞬时冷却速率，且单位为℃/h。
论文[5]中的实验数据图（下图）中大致可以找出700℃时的瞬时冷却速率，大约为95.744680℃/s。

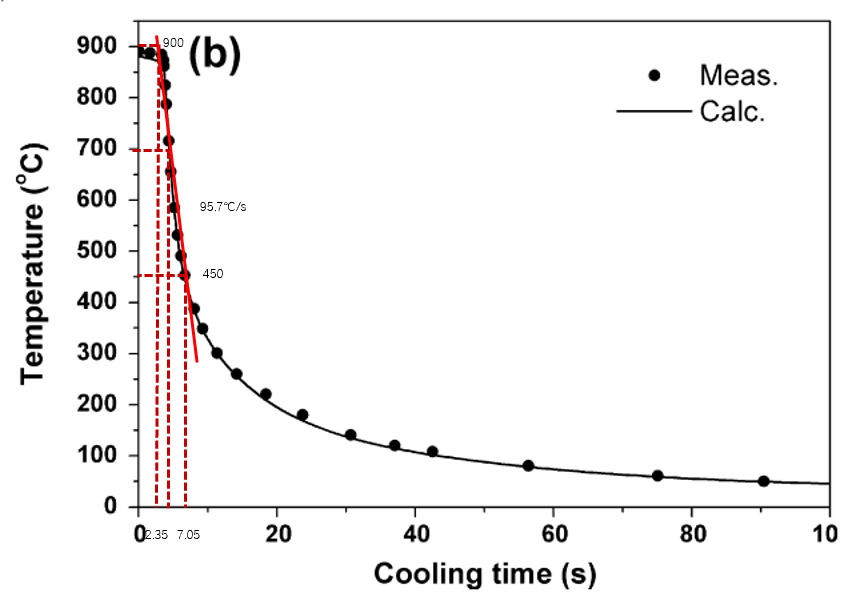
此处需要更严密的文献证明。

提到的冷却速率在温度变化较小范围内是一个定值，那么对其进行单位换算：
\[113.314℃/s=386.5°C/h\] [3]中绘制出了其他钢铁的一些冷却速率曲线，可以发现这个冷却速率是合理的。

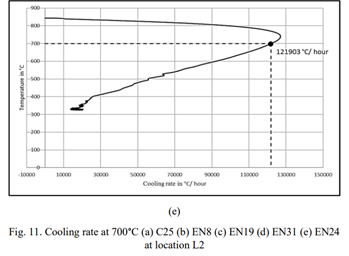
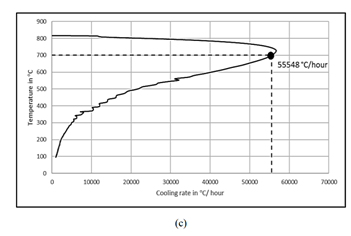
模型搭建

本项目中使用Simulink对整个淬火模型进行建模仿真。

子系统结构

根据式\((5)\)，马氏体的硬度可以表示为如下的系统：

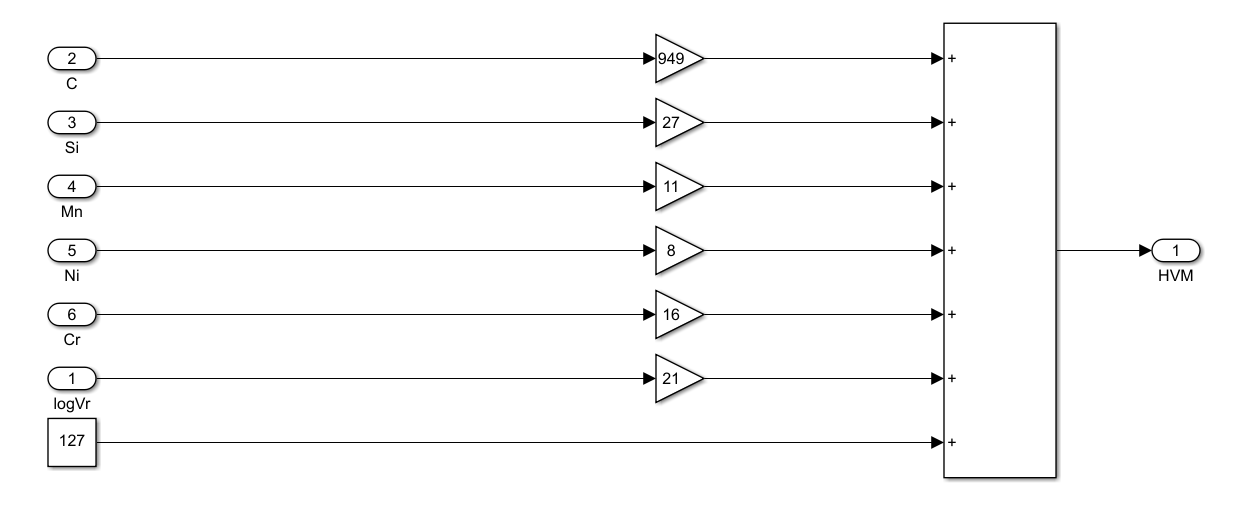
根据式\((6)\)，贝氏体的硬度可以表示为如下的系统：

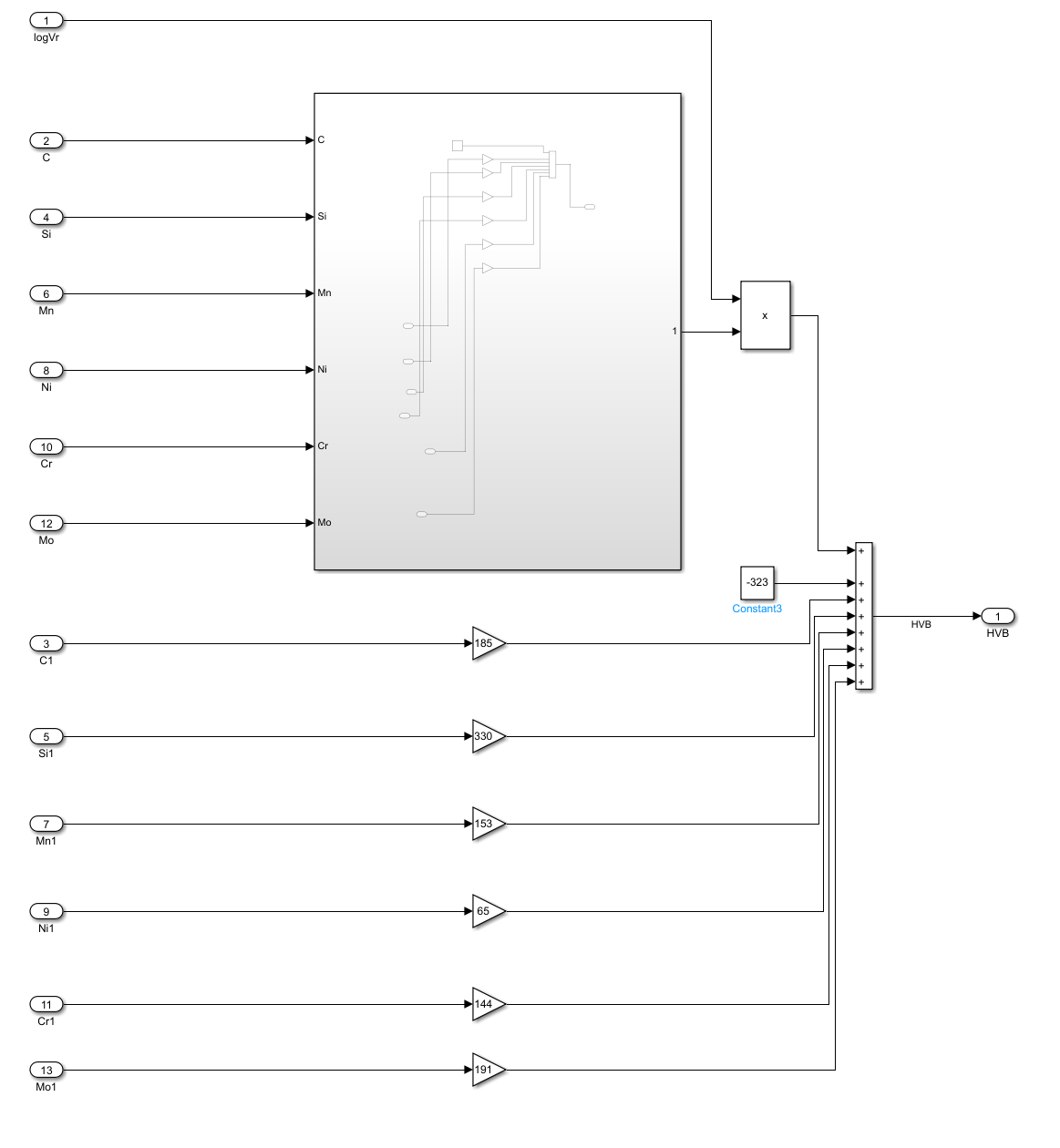
其中的子系统表示\((6)\)中括号内的线性组合：

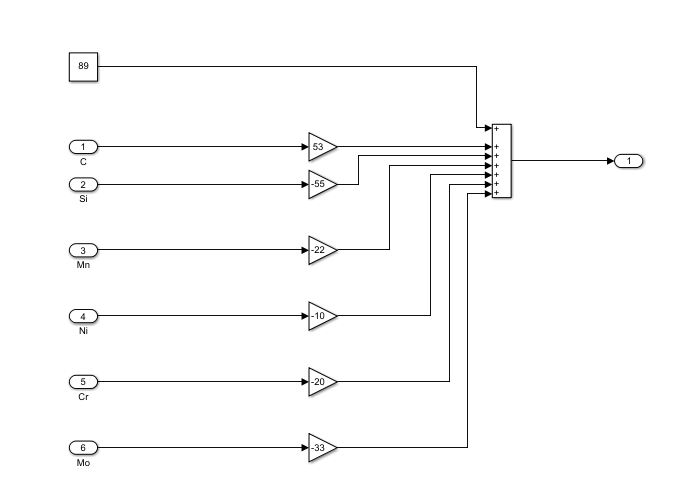
根据式\((7)\)，珠光体和铁氧体的硬度可以表示为如下的系统：

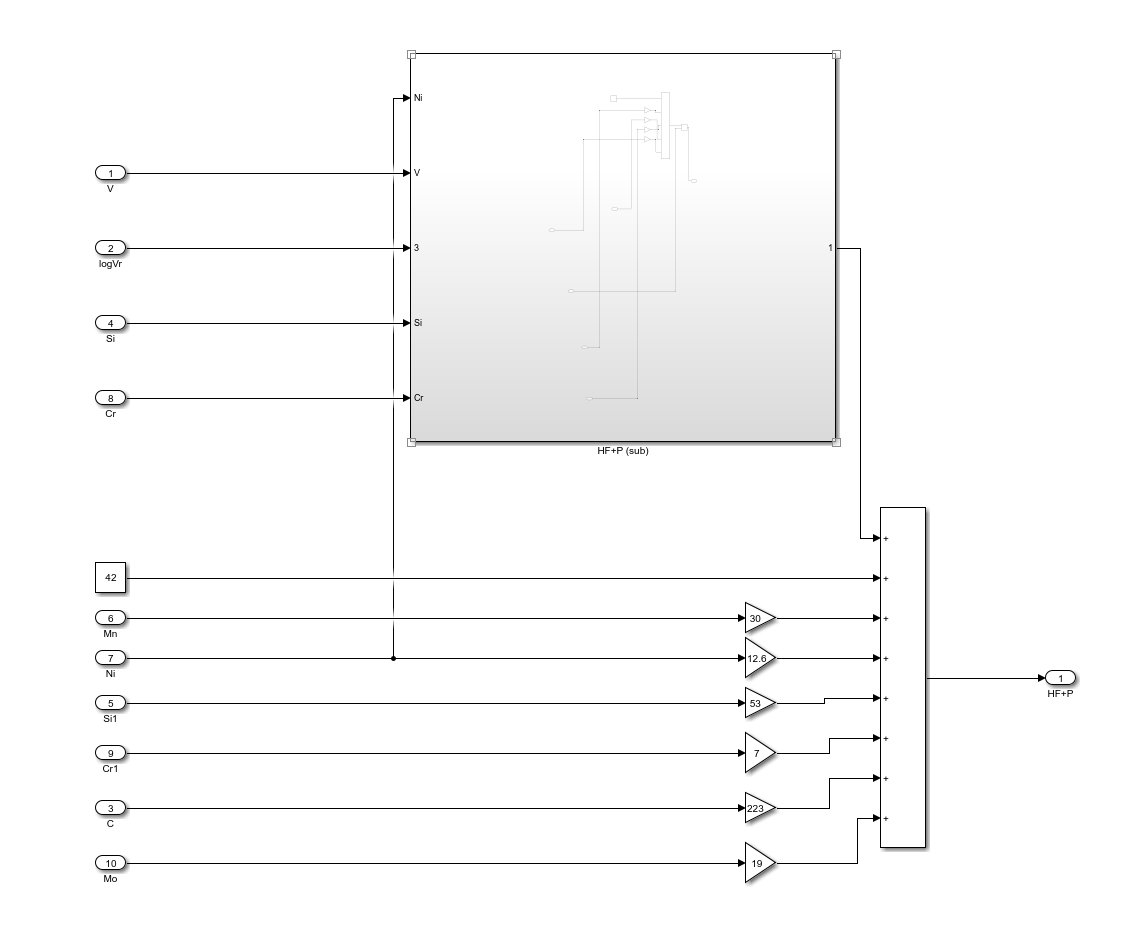
其中的子系统表示\((7)\)中括号内的线性组合：

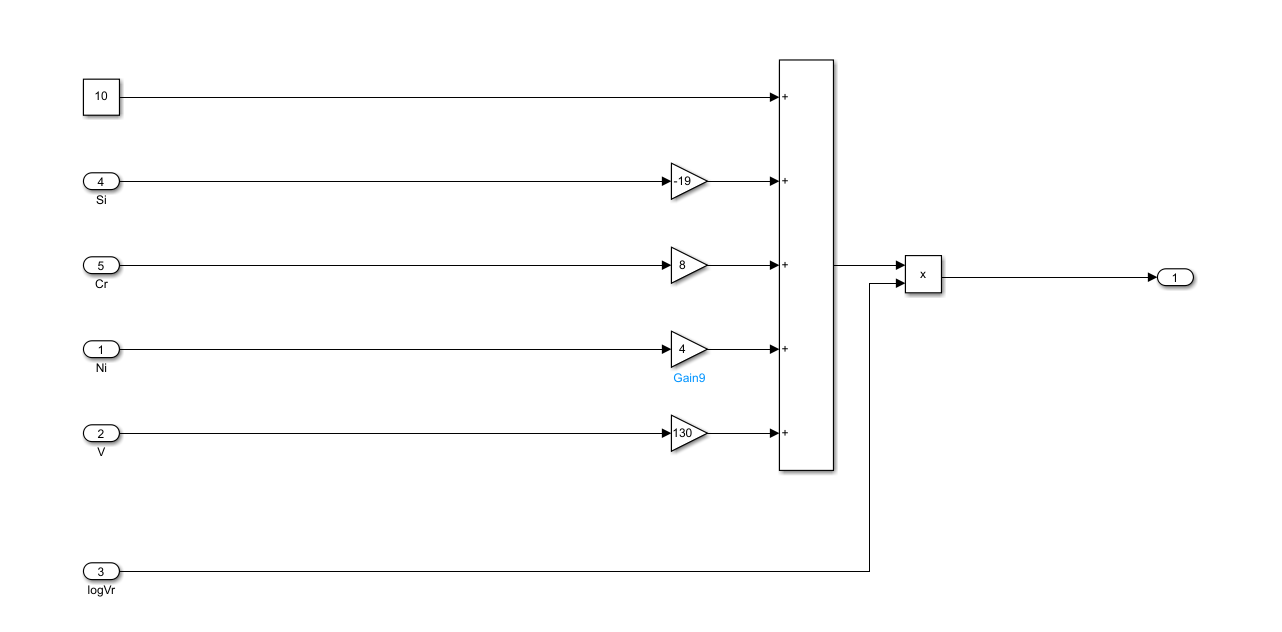
系统输入

元素的采样分布

根据[6]，将C，Si，Mn，Cr，Ni的元素含量分布设置为参数对应的正态分布，如果遵循\(3σ\)原则将\(μ+3σ\)和\(μ-3σ\)点视为最大值和最小值点的话，有：
\[\begin{cases} μ+3σ=max\\ μ-3σ=min \end{cases} \tag{8}\]

元素	C	Si	Mn	Cr	Ni
μ	0.465	0.25	0.075	0.1	0.1
σ	0.005	0.2/6	0.05	0.2/6	0.2/6

每0.1秒整个系统会对所有的正态分布进行随机采样，作为系统的输入。
而[6]中未提到的元素:Mo和V的元素含量分布设置为均值为0.1(%)，方差为0.01(%)的高斯分布。

条件限制

[6]中还限制了Cr和Ni的元素质量分数之和必须小于0.35%:
\[Cr+Ni<0.35\%\] 此处使用Simulink当中的Switch模块，设置Switch的默认输入为1，另一输入为0，条件为\(Cr+Ni>0.35\)时Switch切换到输入0。将Switch的输出和每一个元素的输入连接至乘法器后再分别输入到各子系统中。
如此，当采样到的Cr和Ni的随机数满足\(Cr+Ni>0.35\)时，系统的所有输入都将为0。

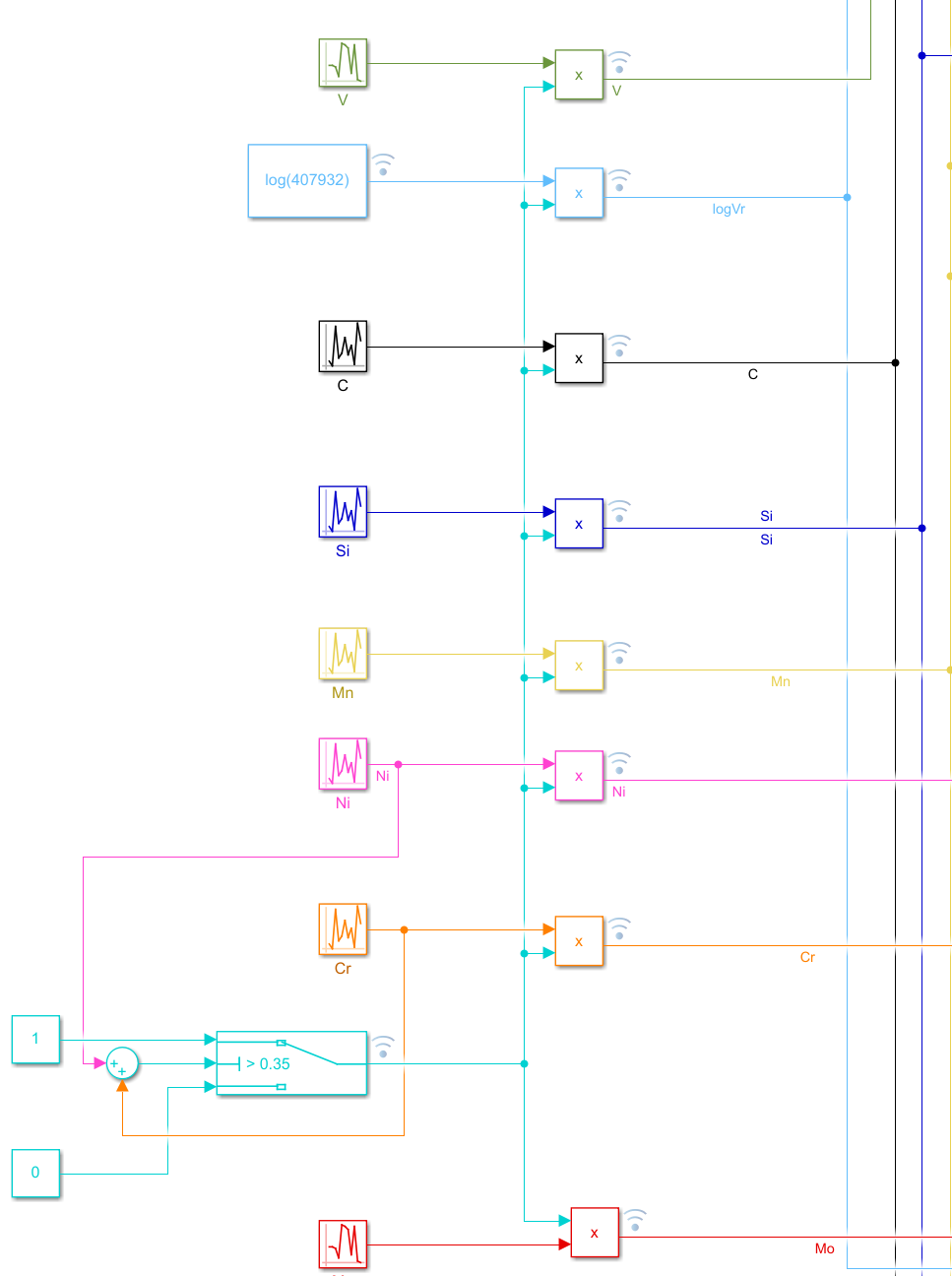
当所有元素输入为0时，由于式\((5)\)-\((7)\)中的常数项，输出仍然不为0，因此需要在输出中利用switch模块转为0：

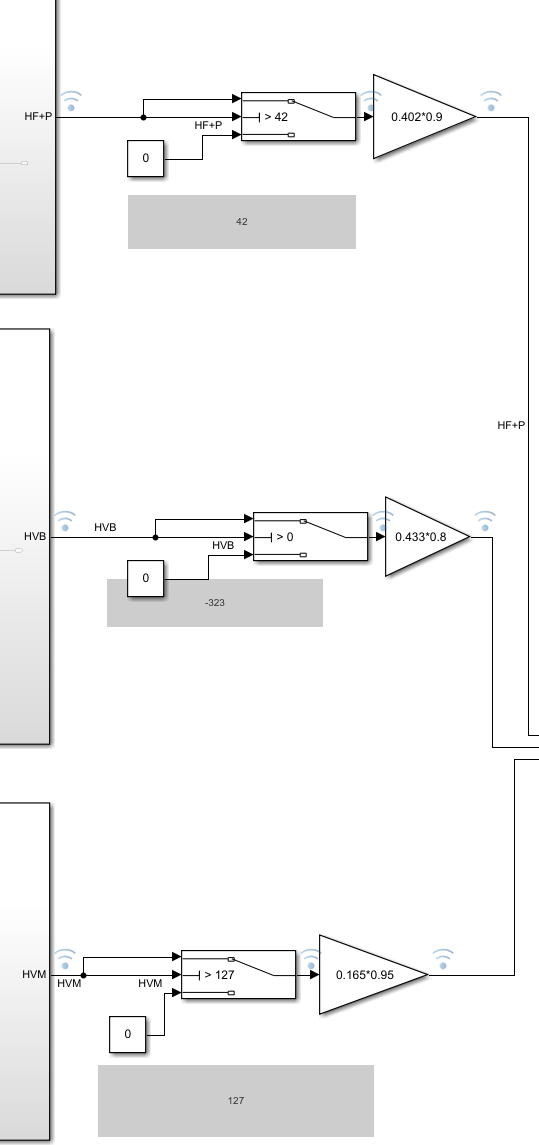
将三个子系统进行封装，并连接对应的输入信号，同时输出乘上对应的权重后相加以满足式\((3)\)，整个系统如下图所示：

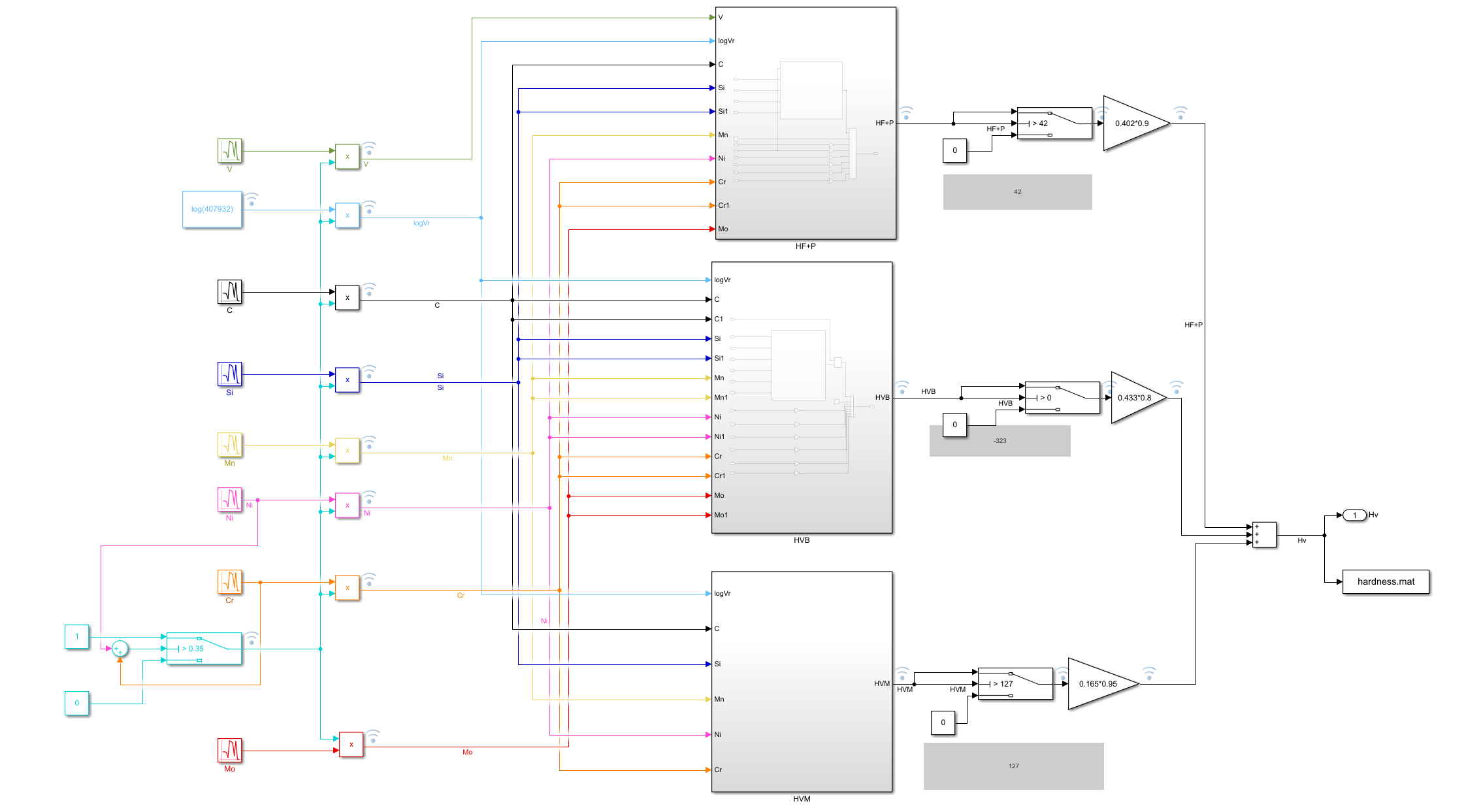
系统简易验证

运行系统，得到最终的输出为：

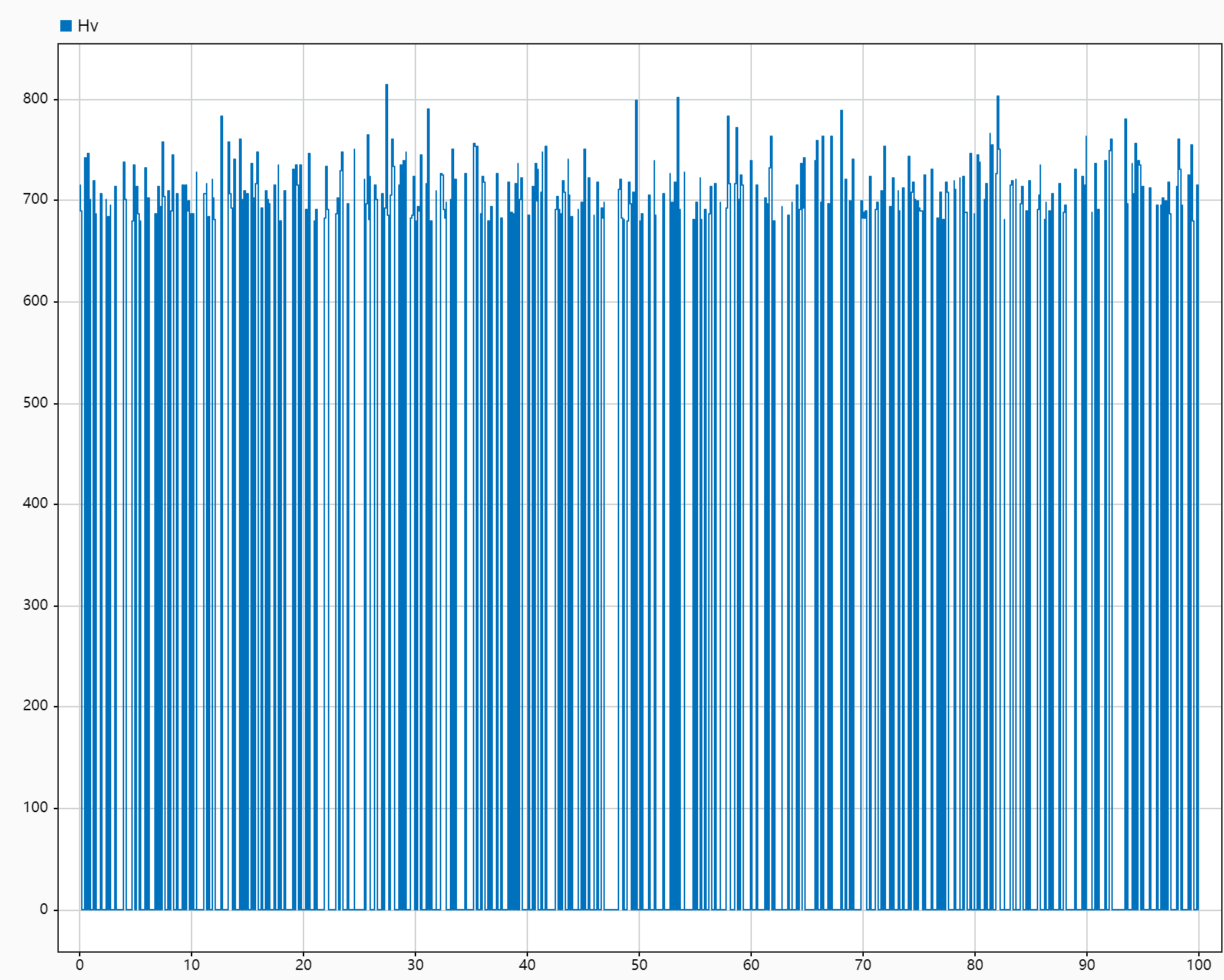
该数据可以通过转换为回火后莫氏硬度(HRC)与已有技术材料进行比较。
根据上图可以初步得到输出钢材的平均值在720HV左右，根据下图所示的硬度转换表，可以发现：

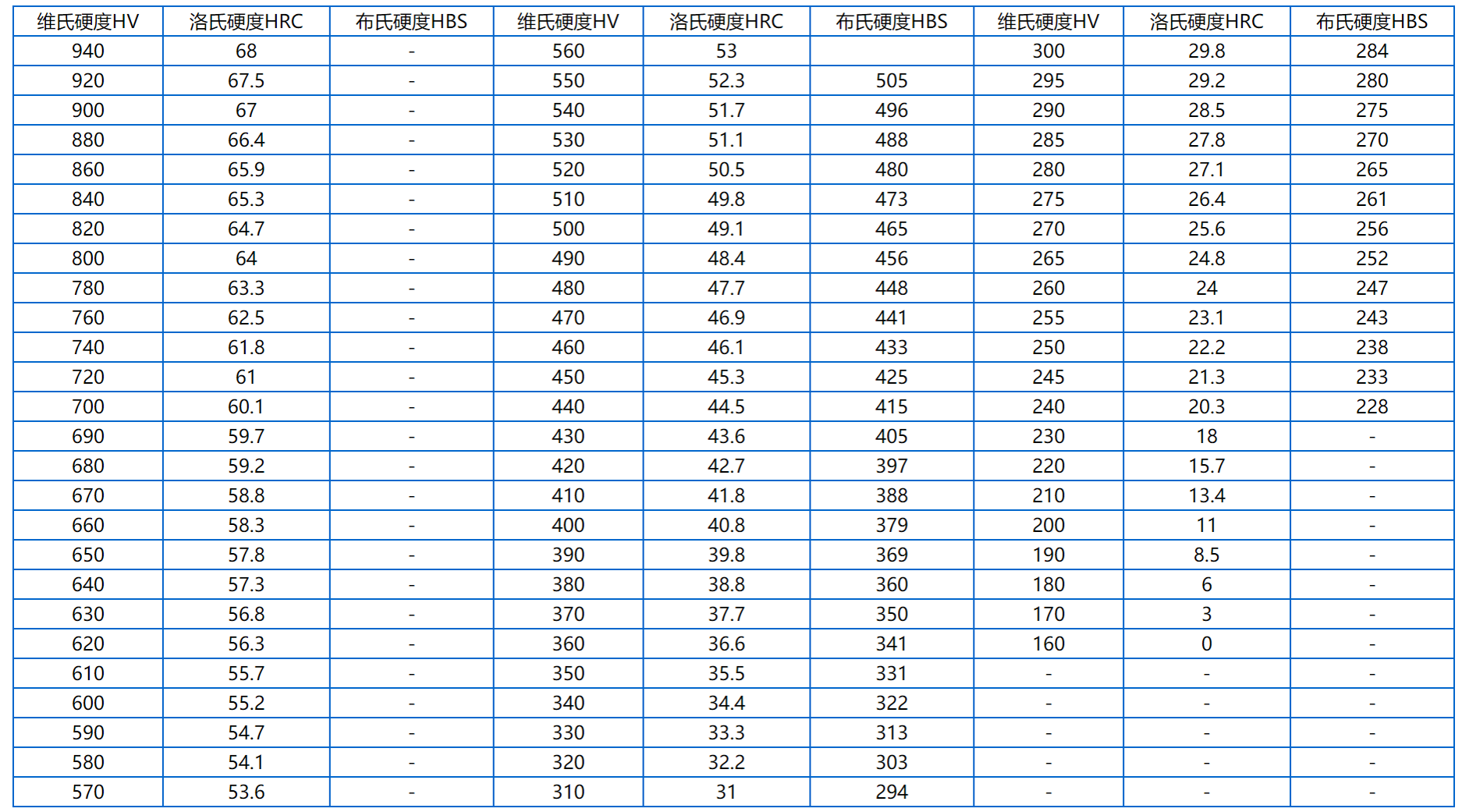
\[720HV≈61HRC\]

该结果符合[7]-[8]中对淬火后硬度的描述。
> [7]機械構造用炭素鋼の焼入れ硬さに及ぼす焼入れ条件の影響，島岡三義・吉田陽亮・大畑直樹・米聡・辻井ありさ，2011。 > [8] Solution for Heat Treatment in Quenching Process of S45C Steel Small Diameter Machine Parts Having Strong Texture, Long Nguyen Nhut Phi, 2018.