并行遗传算法

A Survey of Parallel Genetic Algorithms, Erick Cantu-Paz.

并行化的基本思想是将一个任务分解为彼此独立而且可以同时解决的若干个子任务。遗传算法的执行流程具有潜在的可以将整个任务独立分解为多个独立子任务的特性，这样的性质称为隐式并行性。目前并行的遗传算法可以大致分为三类： 主从遗传算法(master-slave GA)，细粒度遗传算法(fine-grained GA)，和多种群遗传算法(multi-deme GA)（有时也被称为粗粒度遗传算法(coarse-grained GA)）.

主从遗传算法

主从遗传算法(master-slave GA)的基本思想是，在遗传算法的运行过程中，对于每一代种群中每个个体的评估/遗传操作总是相互独立的进行的。
在主从遗传算法中，整个遗传算法集群始终只处理一个种群（因此这种算法又被称为全局单种群遗传算法(global-single population GA)），对于现有种群的选择在主处理器(master processor)中进行；但是在每一代评估（或者是遗传操作，但是很少使用）中，现种群中的个体被分配给若干个从处理器(slave processor)，这些处理器相互独立地完成个体评估任务，然后再将评估（操作）结果上传至主处理器。

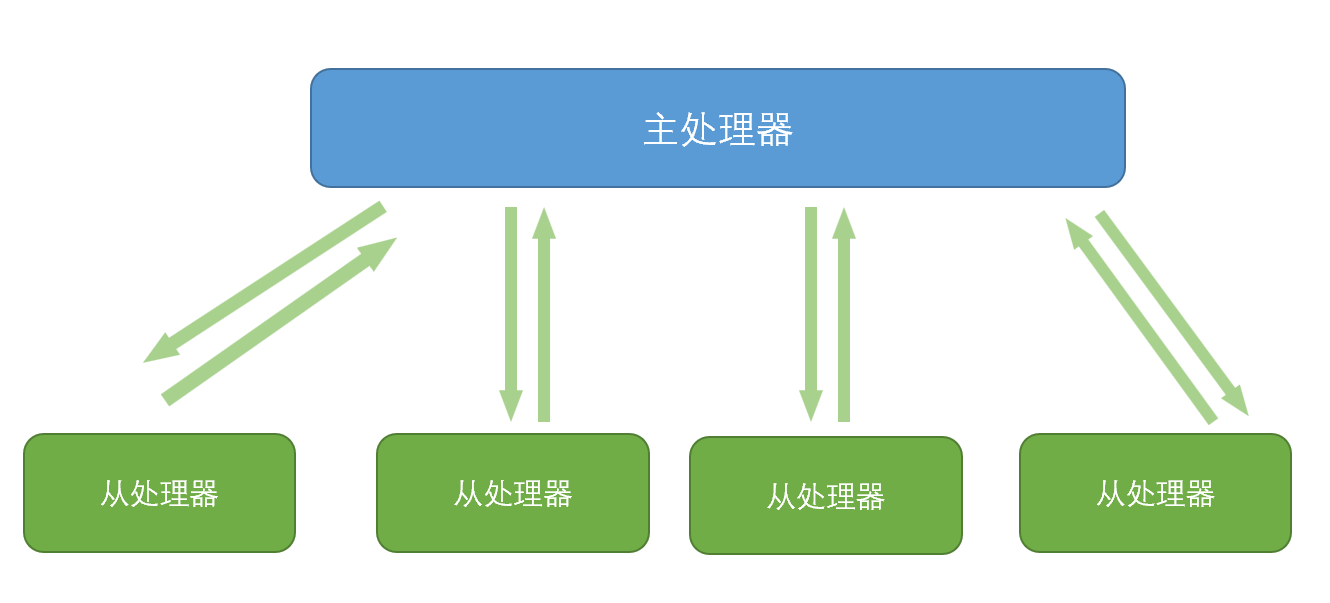
可以发现，主从遗传算法不会影响到遗传算法运行过程的性质，其结果与串行运行的遗传算法结果基本是相同的。

通信方式

在这样的遗传算法运行中，主从处理器之间的通信(communication)仅限于分配个体和上传个体适应度。主从遗传算法的通信方式分为同步通信(synchronous communication)和异步通信(asynchronous communication)两种方式。

• 同步通信
  同步通信是主从遗传算法中最为常见的通信方式：主处理器必须等到所有从处理器上传这一代所有个体的适应度后，才开始进行后续的操作。大多数的主从遗传算法也是采用的同步通信，如此主从遗传算法的特性才会完全和串行遗传算法相同。

• 异步通信
  异步通信更讲究算法运行的速度，它可以通过设置某些机制使得主处理器不用等待某些较慢的从处理器评估结束便开始后续的操作。但是这样的通信方式有可能会使得主从遗传算法的特性与串行遗传算法不同。

从处理器的个数

关于从处理器的个数存在着如下讨论，虽然增加从处理器的个数会节省评估每个个体的时间，与此同时，也会增加主处理器和从处理器的通信时延，因此存在一个最优化的从处理器个数，使得整个算法的运行时间最短。CANTU-PAZE提出从处理器的最优个数应当为:
\[S=\sqrt{\frac{nT_f}{T_c}}\] 其中\(n\)是种群大小;\(T_f\)是单个个体单次评估所需要的时间；\(T_c\)是通信所需的时间。

实现架构

主从遗传算法是一种全局并行的模型，这种模型通常不会对计算机架构有特定的要求。因此主从遗传算法可以在分布式内存(distributed memory computer)和集中式内存(shared-memory computer)的计算机上运行。对于共享同一个内存的多处理器计算机，种群信息可以存储在内存中，任何从处理器都可以从共享的内存中读取指定的个体信息并进行修改。 对于分布式内存的计算机，种群信息可以存放在主处理器的内存中，然后将个体信息分发到指定的从处理器上。

遗传操作的全局并行

主从遗传算法更多的是将个体评估操作进行全局并行化，除此之外，将遗传操作进行全局并行化也是可能的。交叉和变异可以通过将种群分割为若干个子种群再分配给若干从处理器的方式来进行并行化。 然而这些操作在单个处理器上花费的时间非常的短，以至于不可忽略主从处理器通信的时延。如此，主从处理器的通信时延可能会抵消掉全局并行化带来的运算时间的节省。

细粒度遗传算法

细粒度遗传算法(fine-grained GA)是第二种遗传算法并行化的方式，在细粒度遗传算法中，一个处理器处理若干且有限个数的个体，因此，每个子种群可以选择和配对个体的范围都是有限的。不同处理器处理的个体范围边界相互重叠，通过重叠的边界来实现相邻处理器处理个体之间的基因交流。

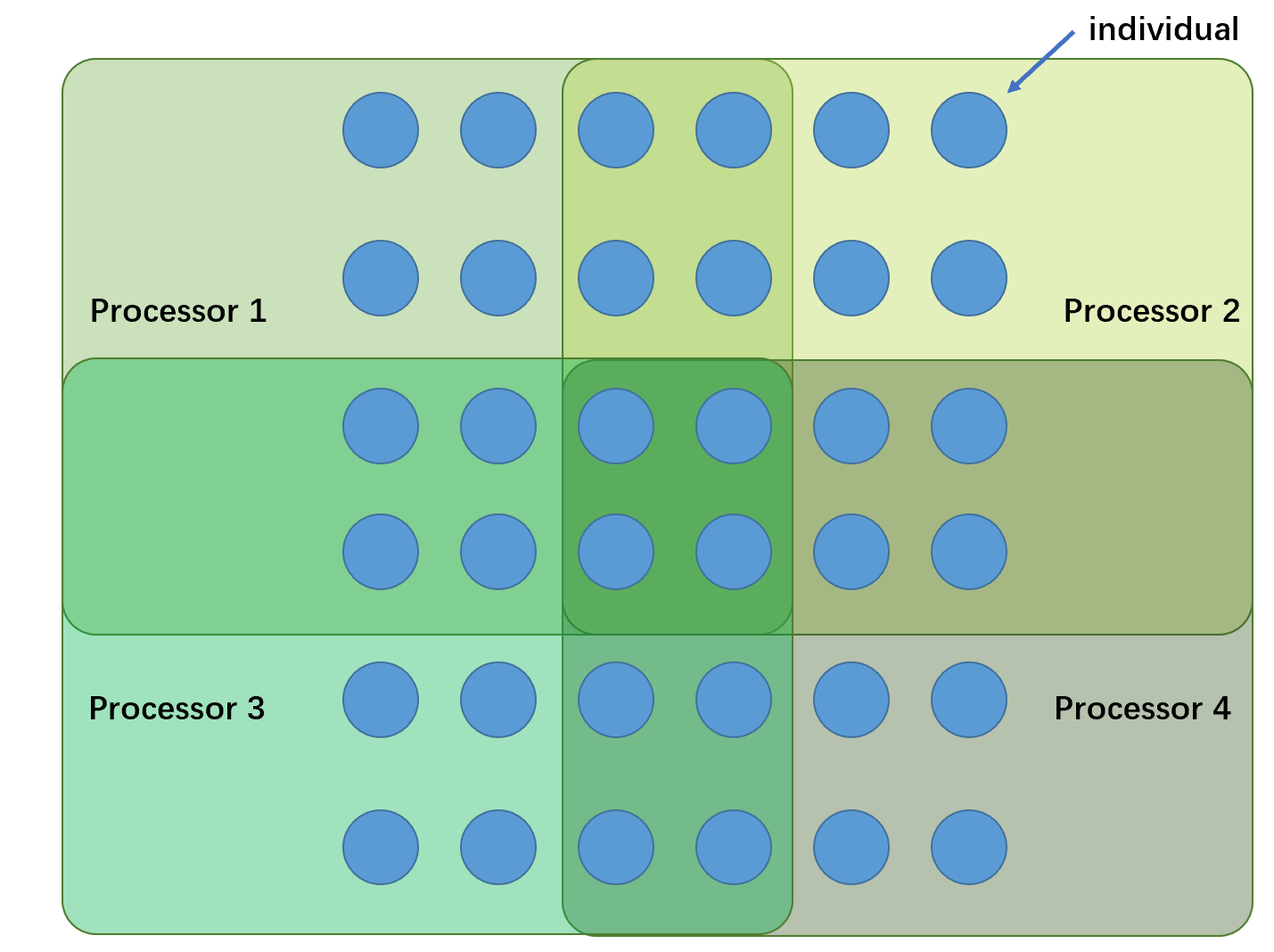
需要注意的是，尽管被分割为了多个处理器处理个体（可以看做是若干个子种群），在全局上看，每一代运行中仍然只具有单个种群。

拓扑结构

细粒度遗传算法的拓扑结构通常是2D网格（形如上面的图示），这是因为许多大规模计算的并行计算机中的拓扑结构是这样的。
在这种拓扑结构中，Manderick和Spiessens等人发现重叠的部分越多，细粒度遗传算法的性能越低下。极端情况下，当所有的子种群彼此涵盖所有个体，那么此时细粒度遗传算法的性能将会和单种群无划分子种群的串行遗传算法相同。
同时，他们也研究了细粒度遗传算法的计算复杂度和时间复杂度：在2D网格的拓扑下，如果子种群大小为\(s\)，染色体长度为\(l\)，那么时间复杂度将会是\(O(s+l)\)或者\(O(s(logs)+l)\)时间步(time steps)，取决于使用的选择机制。

不过大多数的并行计算机具有一个全局路由器，可以将信息转发给任意的处理器，因此其他拓扑结构也可以在基于物理层2D网格结构的基础上实现。
比如Gorges-Schleuter提出的ASPARAGOS算法就是一种细粒度遗传算法，其中用到的拓扑结构形如梯子，每一级的上下分别与其他级的上下边界重叠。

应用

细粒度遗传算法在大规模并行计算中比较受欢迎，较为经典的应用案例是，对于次级RNA结构的预测、装箱问题(bin packing)和时间规划问题(scheduling)。

多种群遗传算法

相比于前两种并行化的方法，多种群遗传算法(multi-population GA/multi-deme GA)要更为复杂，多种群遗传算法中每一代包含了多个子种群，这些种群彼此之间独立进行遗传和进化操作，但是以某种拓扑结构频繁转移和交换一些个体。这样的交换称为迁移(migration)。

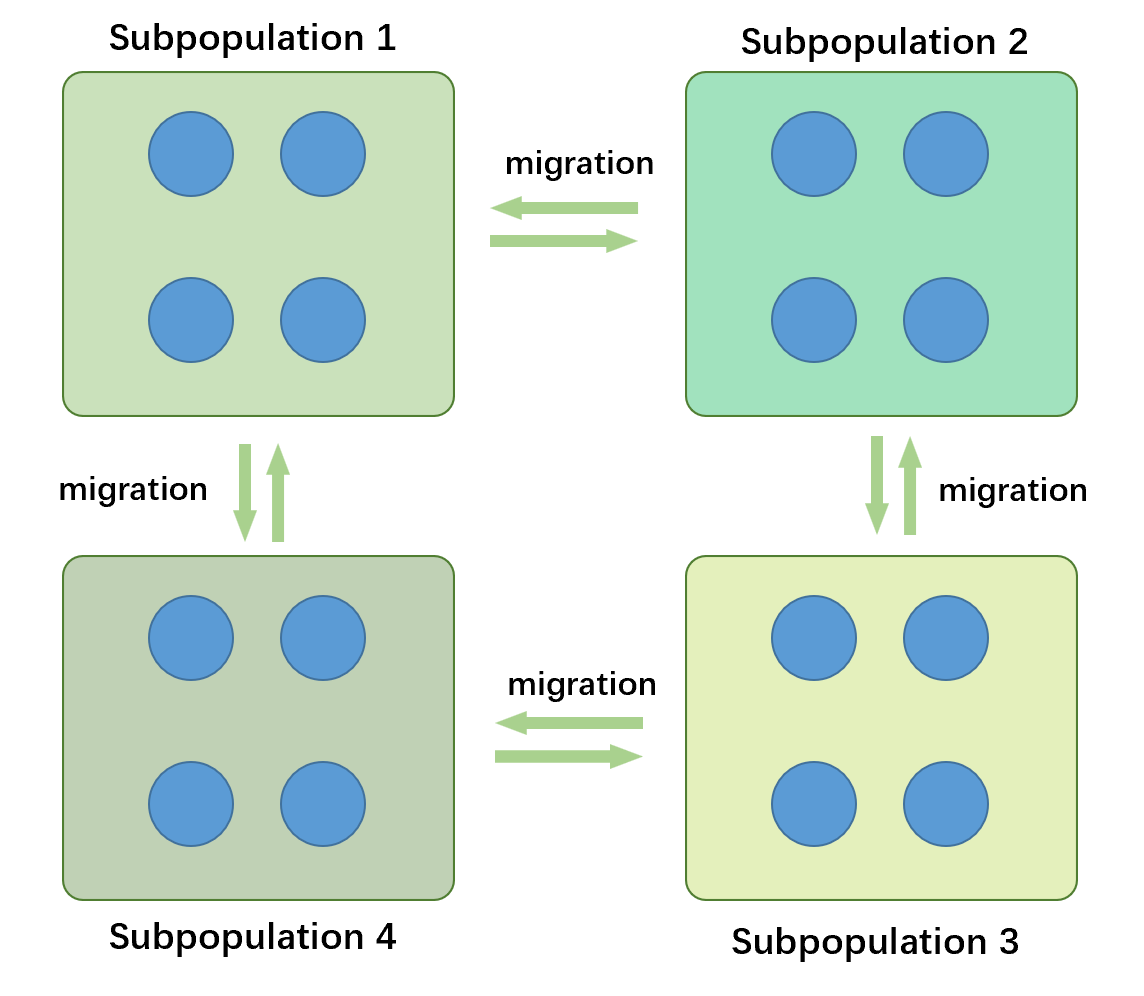
多种群遗传算法是目前最为流行的一种并行化遗传算法的方式，但是其中的一些机制在学界并未能完全理解（比如迁移对进化的作用），相比于单重群遗传算法和经典遗传算法，其机制和行为更加复杂。多种群遗传算法流行的原因可能有如下几点：
- 多种群遗传算法可以被视作是串行遗传算法的延伸。它可以看做是在并行计算机的每个节点上分别运行经典遗传算法，并且在特定的时机交换一些个体。
- 对大多数遗传算法程序，只需要很小的改变就可以将串行遗传算法改造为多种群的并行遗传算法。
- 粗粒度并行的计算机较为常见，且比较容易通过软件进行模拟。

多种群遗传算法也被称为分布式遗传算法(distributed GA)，由于这种遗传算法中计算和通信比率很高，多种群遗传算法也被称为粗粒度遗传算法(coarse-grained GA)。此外，这种思路模拟了生物学中的岛屿进化模型(island model)，群岛之间的生物种群的进化过程相对比较独立，因此也被称为岛模型遗传算法(island GA).

控制参数

子种群大小

第一篇系统性地对于多种群并行遗传算法的研究来源于Grosso等人，通过控制变量实验，该论文作者发现相比于单种群遗传算法，多种群遗传算法中子种群的大小越小，每一代中的平均适应度越高。这样的特性可以通过生物学的现象印证：种群小的时候，有利性状的遗传速度比种群大的时候传播得快。
但是，该论文作者也发现子种群小的时候，种群收敛后的平均适应度要小于大种群收敛后的平均适应度。换句话说，多种群中每个子种群收敛后的个体适应度要小于单种群收敛时候的个体适应度。
另外，Gantu-Paz和Goldberg两人发现，当子种群之间相互隔离时，并行算法的预期速度提升并不是十分明显；其次，当子种群之间进行交流时，并行算法的速度提升更明显。第三，存在一个最优的子种群大小使得对并行算法的速度提升达到最大化。超过这个最优值之后，算法的运行速度会受制于处理器的处理速度。

迁移

Cohoon，Hedge，Martin等人指出了多种群遗传算法与演化生物学理论中的“间断平衡”(Punctuated Equilibria)具有相似之处。间断平衡理论指出，物种可在某一段时间中，经历相对传统观念而言较为快速的物种形成过程，之后又经历一段长时间无太大变化的时期。并且，环境的改变可以促成快速的物种形成过程。根据生态学理论，物种自身的组成也是环境的一部分，物种中不同个体之间存在对资源的竞争。因此，可以通过改变物种自身的组成来改变环境，进而引起快速的物种形成过程。
根据上述理论，多种群遗传算法中的个体迁移可以打断子种群中原本的进化平衡，进而触发新一轮的快速进化。迁移机制会大幅度的提升收敛后的种群平均适应度吗，有些时候甚至比串行遗传算法的收敛适应度还更高。

• 迁移率
  Grosso等人观察到，在低迁移率(migration rate)的情况下，种群仍然表现得很独立，并探索了搜索空间的不同区域。迁徙个体对接收的种群没有明显的影响，解决方案的质量与种群隔离的情况相似。然而，在中等迁移率的情况下，子种群找到的解决方案与在单随机交配种群(panmictic population)中发现的解决方案相似。这些观察结果表明，存在一个临界迁移率，在这个临界迁移率以下，多种群的性能会因隔离而受到阻碍，而在这个临界迁移率以上，多种群找到的解的质量与单种群相同。
  Starkweather和Whitley等人观察到，相对独立的子种群会收敛到不同的个体，迁移和重组可以一定程度上结合部分优秀的解决方案。其次，如果适应度函数不具有可分离性，重组导致个体具有较低的适应度，那么此时串行遗传算法的效果相比并行会更好。

• 迁移的方式
  迁移的方式分为两种：同步和异步。
  同步迁移是指迁移会固定的发生在设置好的间隔后，比如提前设定每多少轮就发生一次迁移，大多数的多种群遗传算法使用这种方式进行迁移。
  异步迁移是指只有当某些指定的情况发生时才会进行迁移，比如当所有的子种群都快要收敛时才进行迁移。 Braun设计的多种群遗传算法中就应用了异步迁移，当所有子种群都完全收敛后再进行迁移，来保证子种群的多样性，避免提前收敛。

• 迁移的时机
  如果迁移过早的发生，此时适应度较高的模式在种群中的占比较小，并不足以影响各子种群的搜索方向，同时还消耗了大量的通信资源。因此普遍认为迁移应当在进化的后期发生。

拓扑结构

传统的对于遗传算法并行化的研究认为：拓扑结构的选择对并行遗传算法的性能可能不是很重要，只需要保证拓扑结构具有高连接性和较小的拓扑直径吗，以保证随着时间的推移子种群间个体可以充分的混合即可。
- 对传播速度的影响
然而更新的研究上，拓扑结构对并行遗传算法的性能影响不可忽视。其中的一个原因是拓扑结构决定了适应度较高的模式传播到所有节点的时间和速度： 如果拓扑结构较为密集，具有较小的传播直径，那么适应度较高的模式将会迅速传播到各个子种群中，并成为优势种群。如果拓扑结构稀疏，具有较大的传播直径，模式的传播速度较慢，各个子种群之间较为孤立并且生成不同的优秀模式，这些模式可能会在更长的时间中融合在一起，整合为更加优秀的个体。
- 对通信资源的影响
另一方面，拓扑结构也影响了通信/迁移所消耗的资源，比如密集型的拓扑结构虽然可以很好的传播好的模式，但是消耗的通信资源也更多。

• 拓扑结构的选择
  综合上述两点，通常采用超立方(hypercube)或者是环形(ring)拓扑结构。
  另一种选择是采用动态的拓扑结构，在动态的拓扑结构下，某个子种群并非固定地与特定的几个子种群进行迁移，而是遵循某些动态规则调整迁移的来源和目标。这样的目的是为了找到对迁移更加敏感的子种群。通常情况下，常见的规则包括子种群的多样性，或者两个子种群间的某些距离度量。

层级并行遗传算法

有一些研究人员尝试将两种不同的并行机制进行融合，基本上融合的方法是在不同层级上使用不同的并行机制，这样的并行遗传算法称为层级并行遗传算法(hierarchical parallel GA)，也是混合并行遗传算法的一种。

比较经典的几种混合方式如下：
- 上层使用多种群遗传算法，下层使用细粒度遗传算法

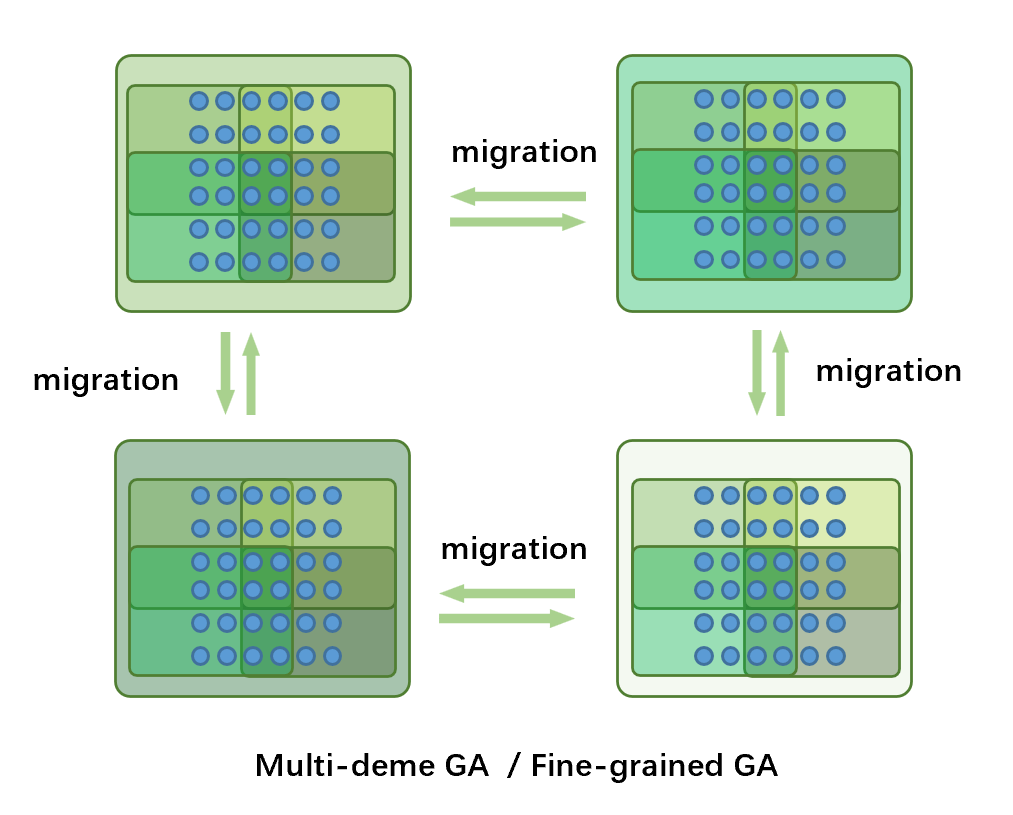
子种群中的个体被重叠划分交付给多个处理器进行，迁移在子种群中进行。

• 上层使用多种群遗传算法，下层使用多种群遗传算法
  
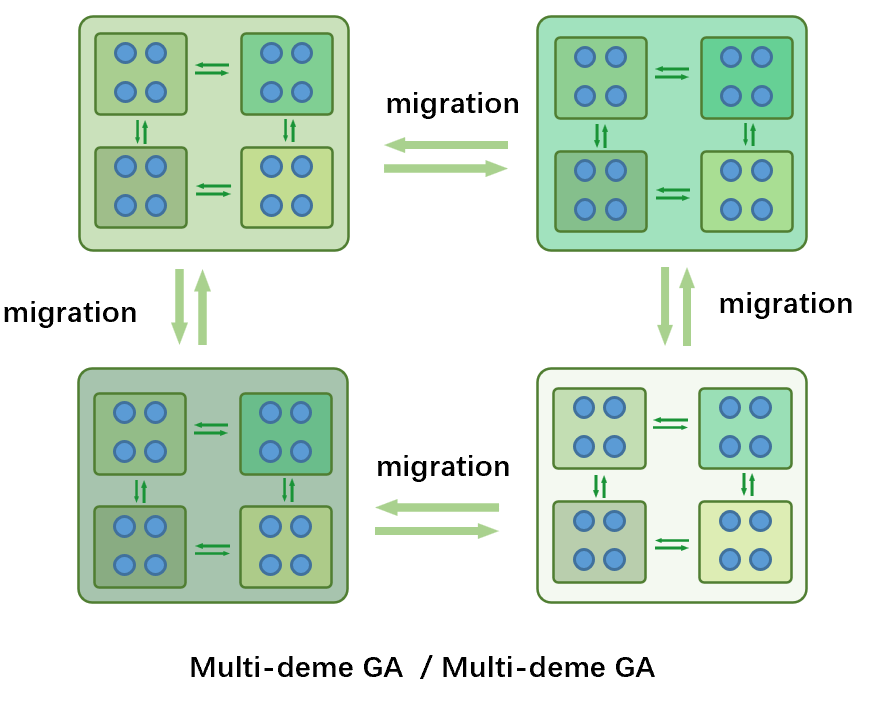
  子种群中被划分为多个独立的子种群，内部相互迁徙的同时，外部的多个子种群也在进行迁徙。

• 上层使用多种群遗传算法，下层使用主从遗传算法
  
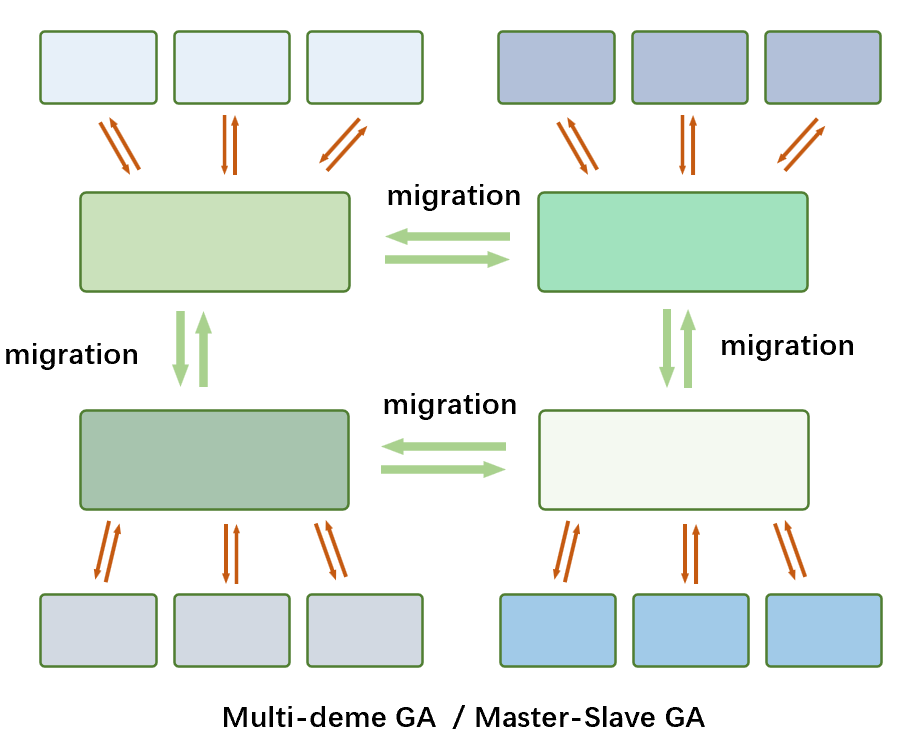
  子种群放置在多个主处理器中，迁移在子种群之间进行，子种群中的个体评估交给各自的从处理器进行。

这样层级融合的并行遗传算法可以成倍地节省计算时间。一种简单的估计层级融合的遗传算法计算速度是将两个层级的并行遗传算法的运行速度相乘。
再者，分层并行的遗传算法可以更加有效地使用更多的处理器，比纯粹的增加多个子种群更能减少算法的运行时间。